Deck 12: Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/162
Play
Full screen (f)
Deck 12: Analysis of Variance
1
A study was recently conducted to see whether the mean starting salaries for graduates of engineering, business, healthcare, and computer information systems majors differ. A random sample of 8 graduates was selected from each major. The following chart shows some of the results of the ANOVA computations; however, some of the output is missing. If it had been included, the calculated test statistic would be F = 8.33. 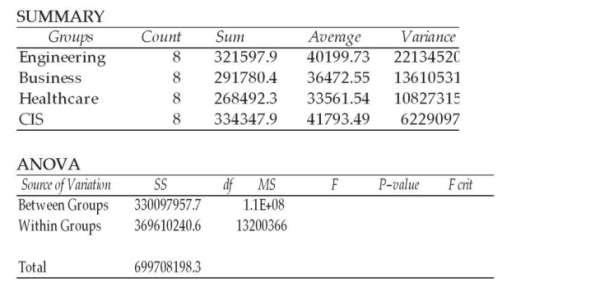

True
2
In conducing one-way analysis of variance, the population distributions are assumed normally distributed.
True
3
In a one-way analysis of variance test, the following null and alternative hypotheses are appropriate: H0 : μ1 = μ2 = μ3 Hα : μ1 ≠ μ2 ≠ μ3
False
4
In conducting one-way analysis of variance, the sample size for each group must be equal.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
5
A company's customer service department wants to compare the average service times at four different service locations. They want to conduct a hypothesis test to determine if all four means are the same or not. If n = 20 observations are taken at each of the four locations, then the degrees of freedom are D1 = 3 and D2 = 19.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
6
In conducting a one-way analysis of variance, if the null hypothesis is true then the variance between groups (MSB) should be approximately equal to the variance within groups (MSW).

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
7
Recently, a company tested three different machine types to see if there was a difference in the mean thickness of products produced by the three. A random sample of ten products was selected from the output from each machine. Given this information, the proper design to test whether the means are equal is a one-way ANOVA balanced design.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
8
A study was recently conducted to see whether the mean starting salaries for graduates of engineering, business, healthcare, and computer information systems majors differ. A random sample of 8 graduates was selected from each major. The following shows the results of the ANOVA computations. However, the degrees of freedom column has been omitted. The correct number of degrees of freedom for the within variation is 28. 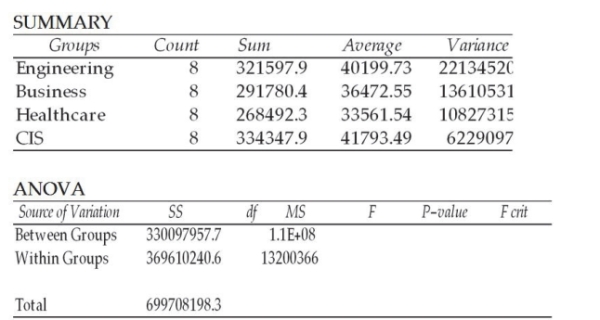


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
9
The term one-way analysis of variance refers to the fact that in conducting the test, there is only one way to set up the null and alternative hypotheses.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
10
Under the basic logic of one-way analysis of variance, if the within variation is large relative to the between variation, it is an indication that the population means are likely to be different.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
11
The within sample variation is the dispersion that exists because the sample means for the various factor levels are not all equal.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
12
A marketing study was recently conducted to see whether the mean monthly sales for a department store located in four cities differ. A random sample of 6 months were selected from each store. Based upon this information, the appropriate null hypothesis to be tested is H0 : μ1 = μ2 = μ3 = μ4

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
13
In a recent one-way ANOVA test, SSW was equal to 15,900 and the SSB was equal to 3,100. Therefore, SST is equal to 12,800.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
14
In a one-way analysis of variance design, there is a single factor of interest but there may be multiple levels of the factor.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
15
In one-way analysis of variance, the within-sample variation is not affected by whether the null hypothesis is true or not.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
16
A study was recently conducted to see whether the mean starting salaries for graduates of engineering, business, healthcare, and computer information systems majors differ. A random sample of 8 graduates was selected from each major. If the test is to be conducted using an alpha = 0.05 level, the critical value will be F = 3.838.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
17
A study was recently conducted to see whether the mean starting salaries for graduates of engineering, business, healthcare, and computer information systems majors differ. A random sample of 8 graduates was selected from each major. The following chart shows some of the results of the ANOVA computations; however, some of the output is missing. Given what is available, the proper conclusion to reach based on the sample data is that the population means could be equal using a 0.05 level of significance. 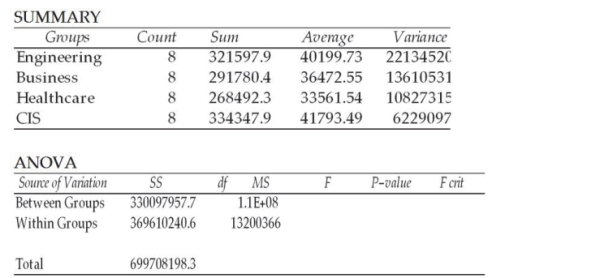


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
18
In a completely randomized analysis of variance design, the observations from each factor are selected in an independent and random fashion.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
19
In a one-way analysis of variance design, the total variation in the data across the various factor levels can be partitioned into two parts, the within sample variation and the between sample variation.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
20
The one-way ANOVA test involves assuming that the population variances are equal.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
21
A national car rental agency is interested in determining whether the mean days that customers rent cars is the same between three of its major cities. The following data reflect the number of days people rented a car for a sample of people in each of three cities. Assuming that a one-way analysis of variance is to be performed, the value of the test statistic is approximately F = 3.4. 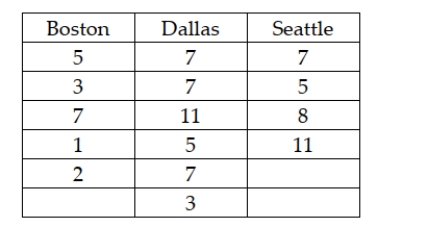


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
22
A fixed effects analysis of variance differs from a random-effects analysis of variance in the way in which the sums of squares are computed.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
23
A national car rental agency is interested in determining whether the mean days that customers rent cars is the same between three of its major cities. The following data reflect the number of days people rented a car for a sample of people in each of three cities. Assuming that a one-way analysis of variance is to be performed, the total sum of squares is computed to be approximately 120.9. 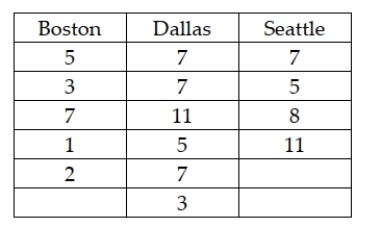


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
24
Three brands of running shoes are each tested by 10 different runners. The amount of wear on the sole of the shoes is then measured. The objective is to determine if there is any difference among the three brands of shoes based on how long the soles last. This means that there is one factor with 10 levels and 3 blocks.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
25
Three brands of running shoes are each tested by 10 different runners. The amount of wear on the sole of the shoes is then measured. The objective is to determine if there is any difference among the three brands of shoes based on how long the soles last. The null hypothesis is: H0 : μ1 = μ2 = μ3.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
26
A national car rental agency is interested in determining whether the mean days that customers rent cars is the same between three of its major cities. The following data reflect the number of days people rented a car for a sample of people in each of three cities. Given this information, the correct null and alternative hypotheses are: 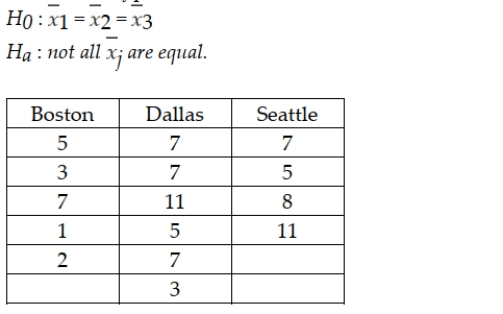


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
27
A company's customer service department wants to compare the average service times at three different service locations. It wants to conduct a hypothesis test to determine if all three means are the same or not, at the 0.05 level of significance. If n =10 observations are taken at each of the three restaurants, the critical value is F = 3.354.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
28
A company has established an experiment with its production process in which three temperature settings are used and five elapsed times are used for each setting. The company then produces one product under each and measures the resulting strength of the product. This experimental design is called a randomized complete block design.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
29
Three brands of running shoes are each tested by 10 different runners. The amount of wear on the sole of the shoes is then measured. The objective is to determine if there is any difference among the three brands of shoes based on how long the soles last. The degrees of freedom for testing whether the brands of shoes differ are D1 = 9 and D2 = 2.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
30
Analysis of variance can only be done for fixed effects.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
31
The Tukey-Kramer method for multiple comparison is used after the analysis of variance F-test has lead us to reject the null hypothesis that all population means are equal.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
32
A company has established an experiment with its production process in which three temperature settings are used and five elapsed times are used for each setting. The company then produces one product under each and measures the resulting strength of the product. The managers are mainly interested in determining whether the mean strength is the same at all temperature settings, but they know that controlling for process time is important. The following data were observed from the experiment: 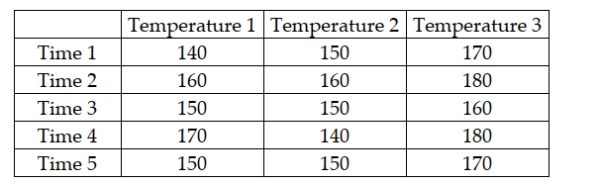 Based on these data and experimental design, the primary null hypothesis to be tested is H0 : μ1 = μ2 = μ3.
Based on these data and experimental design, the primary null hypothesis to be tested is H0 : μ1 = μ2 = μ3.
 Based on these data and experimental design, the primary null hypothesis to be tested is H0 : μ1 = μ2 = μ3.
Based on these data and experimental design, the primary null hypothesis to be tested is H0 : μ1 = μ2 = μ3.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
33
As a step in establishing its rates, an automobile insurance company is interested in determining whether there is a difference in the mean highway speeds that drivers of different age groups drive. To help answer this question, it has selected a random sample of drivers in three age categories: under 21, 21-50, and over 50. The engineers then recorded the drivers' speeds at a designated point on a highway in the state. The subjects were unaware that their speed was being recorded. The following one-way ANOVA output was generated from the sample data. Based upon this output, it is possible that a Type II statistical error has been committed if the null hypothesis is tested at the alpha equal 0.05 level. ANOVA: Single Factor 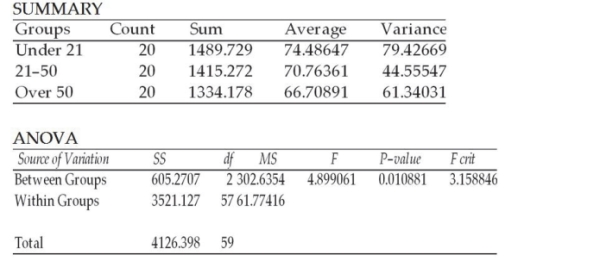


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
34
A randomized complete block analysis of variance allows the analyst to control for sources of variation that might adversely affect the analysis by using the concept of paired samples.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
35
The Tukey-Kramer method for multiple comparisons can only be used when the analysis of variance design is balanced.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
36
The experiment-wide error rate will be higher than the 0.05 significance level if the multiple comparison tests for the mean difference between any two populations use the 0.05 level.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
37
Three brands of running shoes are each tested by 10 different runners. The amount of wear on the sole of the shoes is then measured. The objective is to determine if there is any difference among the three brands of shoes based on how long the soles last. The degrees of freedom for testing whether there is any blocking effect D1 = 9 and D2 = 18.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
38
A company has established an experiment with its production process in which three temperature settings are used and five elapsed times are used for each setting. The company then produces one product under each and measures the resulting strength of the product. The managers are mainly interested in determining whether the mean strength is the same at all temperature settings, but they know that controlling for process time is important. The following data were observed from the experiment: 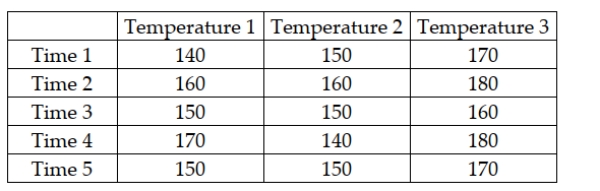 Based on these data and experimental design, for a significance level of 0.05, the managers should conclude that they were justified in blocking on the basis of processing time.
Based on these data and experimental design, for a significance level of 0.05, the managers should conclude that they were justified in blocking on the basis of processing time.
 Based on these data and experimental design, for a significance level of 0.05, the managers should conclude that they were justified in blocking on the basis of processing time.
Based on these data and experimental design, for a significance level of 0.05, the managers should conclude that they were justified in blocking on the basis of processing time.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
39
As a step in establishing its rates, an automobile insurance company is interested in determining whether there is a difference in the mean highway speeds that drivers of different age groups drive. To help answer this question, it has selected a random sample of drivers in three age categories: under 21, 21-50, and over 50. The engineers then recorded the drivers' speeds at a designated point on a highway in the state. The subjects were unaware that their speed was being recorded. The following one-way ANOVA output was generated from the sample data. Based upon this output, if the significance level is 0.05, the engineers should conclude that the mean speeds may all be equal since the p-value is less than alpha. ANOVA: Single Factor 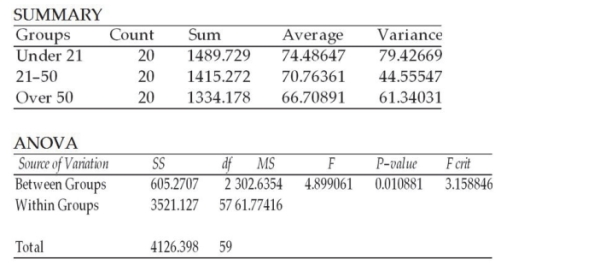


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
40
If the null hypothesis that all population means are equal is rejected by the analysis of variance F-test, the alternative hypothesis that all population means differ is concluded to be true.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
41
In order to analyze any potential interactions between factors in an analysis of variance study, it is necessary to have at least two measurements at each level of each factor.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
42
An advertising company is interested in determining if there is a difference in the mean sales that will be generated for a soft drink company based on which shelf the soft drinks are located. There are four possible shelf levels. The ad company wants to control for store size. The following data reflect the sales for one week at each combination of shelf level and store size. 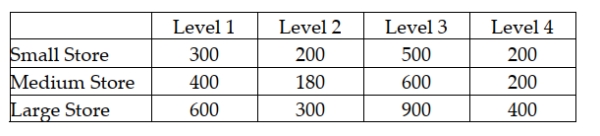 Based on the experimental design, the managers should conclude that they were justified in blocking on store size if they test using a 0.05 level of significance.
Based on the experimental design, the managers should conclude that they were justified in blocking on store size if they test using a 0.05 level of significance.
 Based on the experimental design, the managers should conclude that they were justified in blocking on store size if they test using a 0.05 level of significance.
Based on the experimental design, the managers should conclude that they were justified in blocking on store size if they test using a 0.05 level of significance.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
43
Six food critics each visited and rated four different restaurants. Each critic visited each restaurant on three separate occasions and recorded a score for each visit. The correct method for analyzing this data is two-factor ANOVA.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
44
A study recently conducted by a marketing firm analyzed three different advertising designs and four different income levels of potential customers. At each combination of factor A and factor B, 5 customers are observed and the number of products produced are recorded. The total number of degrees of freedom associated with this two-factor ANOVA design is 59.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
45
In a two-factor ANOVA design with replications, there are three hypotheses to be tested; test for factor A, test for factor B, and test for interaction between factors A and B.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
46
In a two-factor ANOVA design, the variances of the populations are assumed to be equal unless there is interaction present.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
47
In a two-factor ANOVA, the minimum number of replications required in any cell is two, but all cells must have the same number of replications.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
48
A study recently conducted by a marketing firm analyzed three different advertising designs and four different income levels of potential customers. At each combination of factor A and factor B, 5 customers are observed and the number of products produced are recorded. The degrees of freedom for the MSE in this two-factor ANOVA design is 48.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
49
An advertising company is interested in determining if there is a difference in the mean sales that will be generated for a soft drink company based on which shelf the soft drinks are located. There are four possible shelf levels. The ad company wants to control for store size. The following data reflect the sales for one week at each combination of shelf level and store size. 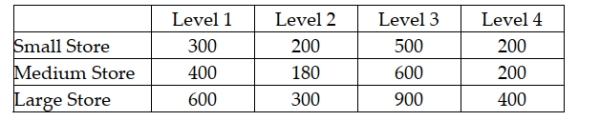 Based on the experimental design, the number of treatments is two.
Based on the experimental design, the number of treatments is two.
 Based on the experimental design, the number of treatments is two.
Based on the experimental design, the number of treatments is two.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
50
Six food critics each visited and rated four different restaurants. Each critic visited each restaurant on three separate occasions and recorded a score for each visit. The total number of degrees of freedom is 71.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
51
In a two-factor ANOVA study, if the two factors do not interact, then neither factor A nor factor B can be considered statistically significant.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
52
In a two-factor ANOVA, the total sum of squares can be partitioned into four parts; the variation due to factor A, the variation due to factor B, the variation due to blocking, and the error variation.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
53
Interaction is the term that is used in a two-factor ANOVA design when the two factors have different means.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
54
Based on the partially completed ANOVA table below, we know that 3 samples are being compared using 9 blocks. 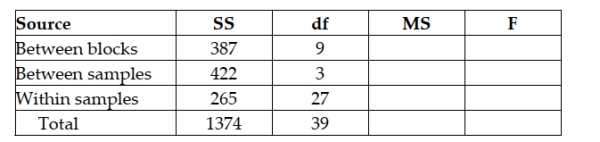


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
55
The number of cells in a two-factor analysis of variance design is equal to the number of levels of factor A plus the number of levels of factor B.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
56
An advertising company is interested in determining if there is a difference in the mean sales that will be generated for a soft drink company based on which shelf the soft drinks are located. There are four possible shelf levels. The ad company wants to control for store size. The following data reflect the sales for one week at each combination of shelf level and store size. 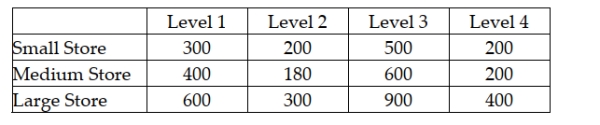 Based on the experimental design, the calculated F-test statistic value for testing whether blocking on store size was effective is approximately 16.3.
Based on the experimental design, the calculated F-test statistic value for testing whether blocking on store size was effective is approximately 16.3.
 Based on the experimental design, the calculated F-test statistic value for testing whether blocking on store size was effective is approximately 16.3.
Based on the experimental design, the calculated F-test statistic value for testing whether blocking on store size was effective is approximately 16.3.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
57
Given the partially completed ANOVA table below, the test statistic for determining if there is any blocking effect is F = 4.38. 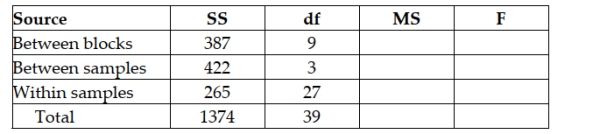


Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
58
Six food critics each visited and rated four different restaurants. Each critic visited each restaurant on three separate occasions and recorded a score for each visit. The critical value for testing whether there is any difference among the four restaurants, using the 0.05 level of significance is approximately F = 2.8.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
59
Six food critics each visited and rated four different restaurants. Each critic visited each restaurant on three separate occasions and recorded a score for each visit. The number of degrees of freedom in the interaction row of the ANOVA table is 15.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
60
To test for the stopping distances of four brake systems, 10 of the same make and model of car are selected randomly and then are assigned randomly to each of four brake systems. This is a randomized complete block design.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
61
In a two-factor ANOVA design with replication, if the null hypothesis pertaining to interaction between factors A and B is rejected, then it is recommended that the hypothesis tests for factor A and factor B individually should not be conducted because the conclusions might be misleading.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
62
An Internet service provider is interested in testing to see if there is a difference in the mean weekly connect time for users who come into the service through a dial-up line, DSL, or cable Internet. To test this, the ISP has selected random samples from each category of user and recorded the connect time during a week period. The following data were collected: 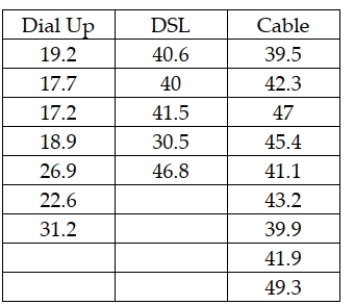 Based upon these data and a significance level of 0.05, which of the following statements is true?
Based upon these data and a significance level of 0.05, which of the following statements is true?
A) The F-critical value for the test is 3.555
B) The test statistic is approximately 43.9
C) The null hypothesis should be rejected and conclude that the mean connect times for the three user categories are not all equal.
D) All of the above are true.
 Based upon these data and a significance level of 0.05, which of the following statements is true?
Based upon these data and a significance level of 0.05, which of the following statements is true?A) The F-critical value for the test is 3.555
B) The test statistic is approximately 43.9
C) The null hypothesis should be rejected and conclude that the mean connect times for the three user categories are not all equal.
D) All of the above are true.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
63
A hotel chain has four hotels in Oregon. The general manager is interested in determining whether the mean length of stay is the same or different for the four hotels. She selects a random sample of n = 20 guests at each hotel and determines the number of nights they stayed. Assuming that she plans to test this using an alpha level equal to 0.05, which of the following is the correct critical value?
A) F = 3.04
B) F = 2.76
C) t = 1.9917
D) F = 2.56
A) F = 3.04
B) F = 2.76
C) t = 1.9917
D) F = 2.56

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
64
The State Transportation Department is thinking of changing its speed limit signs. It is considering two new options in addition to the existing sign design. At question is whether the three sign designs will produce the same mean speed. To test this, the department has conducted a limited test in which a stretch of roadway was selected. With the original signs up, a random sample of 30 cars was selected and the speeds were measured. Then, on different days, the two new designs were installed, 30 cars each day were sampled, and their speeds were recorded. Suppose that the following summary statistics were computed based on the data: 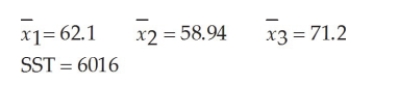 Based on these sample results and a significance level equal to 0.05, assuming that the null hypothesis of equal means has been rejected, the Tukey-Kramer critical range is:
Based on these sample results and a significance level equal to 0.05, assuming that the null hypothesis of equal means has been rejected, the Tukey-Kramer critical range is:
A) 1.96.
B) approximately 4.0.
C) Can't be determined without more information
D) None of the above
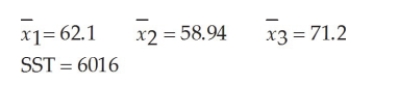 Based on these sample results and a significance level equal to 0.05, assuming that the null hypothesis of equal means has been rejected, the Tukey-Kramer critical range is:
Based on these sample results and a significance level equal to 0.05, assuming that the null hypothesis of equal means has been rejected, the Tukey-Kramer critical range is:A) 1.96.
B) approximately 4.0.
C) Can't be determined without more information
D) None of the above

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
65
The State Transportation Department is thinking of changing its speed limit signs. It is considering two new options in addition to the existing sign design. At question is whether the three sign designs will produce the same mean speed. To test this, the department has conducted a limited test in which a stretch of roadway was selected. With the original signs up, a random sample of 30 cars was selected and the speeds were measured. Then, on different days, the two new designs were installed, 30 cars each day were sampled, and their speeds were recorded. Suppose that the following summary statistics were computed based on the data: 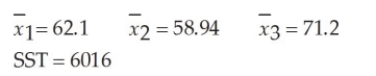 Based on these sample results and significance level equal to 0.05, the sum of squares between is:
Based on these sample results and significance level equal to 0.05, the sum of squares between is:
A) approximately 3,586.
B) approximately 2,430.
C) approximately 1,215.
D) None of the above
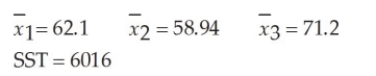 Based on these sample results and significance level equal to 0.05, the sum of squares between is:
Based on these sample results and significance level equal to 0.05, the sum of squares between is:A) approximately 3,586.
B) approximately 2,430.
C) approximately 1,215.
D) None of the above

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
66
In conducting a one-way analysis of variance where the test statistic is less than the critical value, which of the following is correct?
A) Conclude that the means are not all the same and that that the Tukey-Kramer procedure should be conducted.
B) Conclude that the means are not all the same and that that the Tukey-Kramer procedure is not needed.
C) Conclude that all means are the same and that the Tukey-Kramer procedure should be conducted.
D) Conclude that all means are the same and there is no need to conduct the Tukey-Kramer procedure.
A) Conclude that the means are not all the same and that that the Tukey-Kramer procedure should be conducted.
B) Conclude that the means are not all the same and that that the Tukey-Kramer procedure is not needed.
C) Conclude that all means are the same and that the Tukey-Kramer procedure should be conducted.
D) Conclude that all means are the same and there is no need to conduct the Tukey-Kramer procedure.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
67
The general idea is that interaction between two factors means that the effect due to one of the factors is not uniform across all levels of the other factor.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
68
In a one-way analysis of variance test in which the levels of the factor being analyzed are randomly selected from a large set of possible factors, the design is referred to as:
A) a fixed-effects design.
B) a random-effects design.
C) an undetermined results design.
D) a balanced design.
A) a fixed-effects design.
B) a random-effects design.
C) an undetermined results design.
D) a balanced design.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
69
Assume you are conducting a one-way analysis of variance using a 0.05 level of significance and have found that the p-value = 0.06. Which of the follow is correct regarding what you can conclude?
A) Do not reject the null hypothesis; the means are all the same.
B) Reject the null hypothesis; the means are not all the same.
C) Do not reject the null hypothesis; the means are not all the same.
D) Reject the null hypothesis; the means are all the same.
A) Do not reject the null hypothesis; the means are all the same.
B) Reject the null hypothesis; the means are not all the same.
C) Do not reject the null hypothesis; the means are not all the same.
D) Reject the null hypothesis; the means are all the same.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
70
A fast food chain operation is interested in determining whether the mean per customer purchase differs by day of the week. To test this, it has selected random samples of customers for each day of the week. The analysts then ran a one-way analysis of variance generating the following output: ANOVA: Single Factor 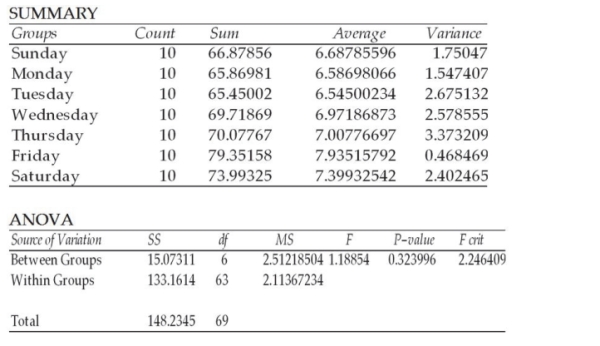 Based upon this output, which of the following statements is true if the test is conducted at the 0.05 level of significance?
Based upon this output, which of the following statements is true if the test is conducted at the 0.05 level of significance?
A) There is no basis for concluding that mean sales is different for the different days of the week.
B) Based on the p-value, the null hypothesis should be rejected since the p-value exceeds the alpha level.
C) The experiment is conducted as an unbalanced design.
D) Based on the critical value, the null should be rejected.
 Based upon this output, which of the following statements is true if the test is conducted at the 0.05 level of significance?
Based upon this output, which of the following statements is true if the test is conducted at the 0.05 level of significance?A) There is no basis for concluding that mean sales is different for the different days of the week.
B) Based on the p-value, the null hypothesis should be rejected since the p-value exceeds the alpha level.
C) The experiment is conducted as an unbalanced design.
D) Based on the critical value, the null should be rejected.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
71
An Internet service provider is interested in testing to see if there is a difference in the mean weekly connect time for users who come into the service through a dial-up line, DSL, or cable Internet. To test this, the ISP has selected random samples from each category of user and recorded the connect time during a week period. The following data were collected: 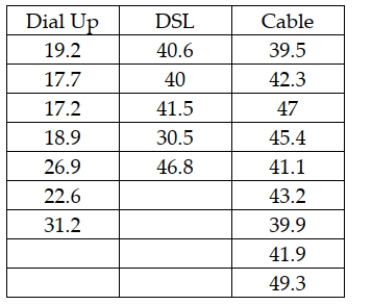 Assuming that the test is to be conducted at a 0.01 level of significance, what would the critical value be for this test?
Assuming that the test is to be conducted at a 0.01 level of significance, what would the critical value be for this test?
A) F = 1.93
B) F = 3.555
C) t = 2.8784
D) F = 6.013
 Assuming that the test is to be conducted at a 0.01 level of significance, what would the critical value be for this test?
Assuming that the test is to be conducted at a 0.01 level of significance, what would the critical value be for this test?A) F = 1.93
B) F = 3.555
C) t = 2.8784
D) F = 6.013

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
72
In a two-factor ANOVA with replication in which all hypotheses are to be tested using an alpha = .05 level, if the p-value for interaction is .03467, the decision maker should conclude that no interaction is present.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
73
The State Transportation Department is thinking of changing its speed limit signs. It is considering two new options in addition to the existing sign design. At question is whether the three sign designs will produce the same mean speed. To test this, the department has conducted a limited test in which a stretch of roadway was selected. With the original signs up, a random sample of 30 cars was selected and the speeds were measured. Then, on different days, the two new designs were installed, 30 cars each day were sampled, and their speeds were recorded. Suppose that the following summary statistics were computed based on the data: 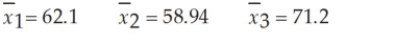 Based on these sample results and significance level equal to 0.05, what is the critical value for this hypothesis test?
Based on these sample results and significance level equal to 0.05, what is the critical value for this hypothesis test?
A) F = approximately 3.15
B) F = approximately 4.90
C) F = approximately 29.47
D) F = approximately 2.70
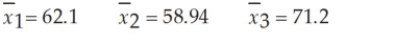 Based on these sample results and significance level equal to 0.05, what is the critical value for this hypothesis test?
Based on these sample results and significance level equal to 0.05, what is the critical value for this hypothesis test?A) F = approximately 3.15
B) F = approximately 4.90
C) F = approximately 29.47
D) F = approximately 2.70

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
74
In a two-factor ANOVA design with replication, the null hypothesis for testing whether interaction exists is that no interaction exists. The alternative hypothesis is that interaction does exist.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
75
Which of the following is an assumption for the one-way analysis of variance experimental design?
A) All populations are normally distributed.
B) The populations have equal variances.
C) The observations are independent.
D) All of the above
A) All populations are normally distributed.
B) The populations have equal variances.
C) The observations are independent.
D) All of the above

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
76
Six food critics each visited and rated four different restaurants. Each critic visited each restaurant on three separate occasions and recorded a score for each visit. Assume that results show that there is an interaction. This would mean that, for example, which restaurant is rated the highest depends on which critic does the rating.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
77
The State Transportation Department is thinking of changing its speed limit signs. It is considering two new options in addition to the existing sign design. At question is whether the three sign designs will produce the same mean speed. To test this, the department has conducted a limited test in which a stretch of roadway was selected. With the original signs up, a random sample of 30 cars was selected and the speeds were measured. Then, on different days, the two new designs were installed, 30 cars each day were sampled, and their speeds were recorded. Suppose that the following summary statistics were computed based on the data: 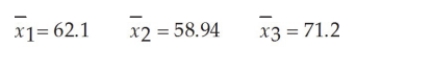 The appropriate test to conduct to determine if the population means are equal is:
The appropriate test to conduct to determine if the population means are equal is:
A) Hartley's F-max test.
B) one-way analysis of variance.
C) three sample t-test.
D) randomized complete block analysis of variance.
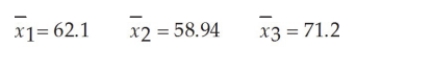 The appropriate test to conduct to determine if the population means are equal is:
The appropriate test to conduct to determine if the population means are equal is:A) Hartley's F-max test.
B) one-way analysis of variance.
C) three sample t-test.
D) randomized complete block analysis of variance.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
78
An Internet service provider is interested in testing to see if there is a difference in the mean weekly connect time for users who come into the service through a dial-up line, DSL, or cable Internet. To test this, the ISP has selected random samples from each category of user and recorded the connect time during a week period. The following data were collected: 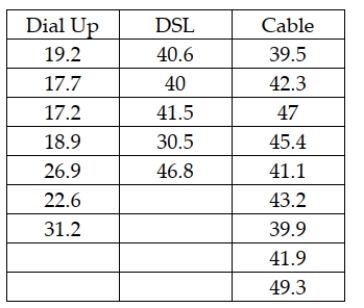 Which of the following would be the correct alternative hypotheses for the test to be conducted?
Which of the following would be the correct alternative hypotheses for the test to be conducted?
A) H0 : μ1 = μ2 = μ3
B) H0 : μ1 ≠ μ2 ≠μ3
C) Not all population means are equal.
D) σ1 = σ2 = σ3 = σ4
 Which of the following would be the correct alternative hypotheses for the test to be conducted?
Which of the following would be the correct alternative hypotheses for the test to be conducted?A) H0 : μ1 = μ2 = μ3
B) H0 : μ1 ≠ μ2 ≠μ3
C) Not all population means are equal.
D) σ1 = σ2 = σ3 = σ4

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
79
A hotel chain has four hotels in Oregon. The general manager is interested in determining whether the mean length of stay is the same or different for the four hotels. She selects a random sample of n = 20 guests at each hotel and determines the number of nights they stayed. Assuming that she plans to test this using an alpha level equal to 0.05, which of the following is the appropriate alternative hypothesis?
A)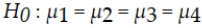
B)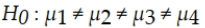
C) Not all population means are equal.
D)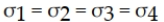
A)
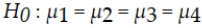
B)
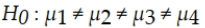
C) Not all population means are equal.
D)
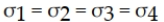

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
80
A study recently conducted by a marketing firm analyzed three different advertising designs (factor
A) and four different income levels (factor
B) of potential customers. At each combination of factor A and
factor B, 5 customers are observed and the number of products produced is recorded. Interaction between
the two factors would exist if low income customers have higher mean buying when design 1 is used, but
higher income customers have higher mean buying when designs 2 and 3 are used.
A) and four different income levels (factor
B) of potential customers. At each combination of factor A and
factor B, 5 customers are observed and the number of products produced is recorded. Interaction between
the two factors would exist if low income customers have higher mean buying when design 1 is used, but
higher income customers have higher mean buying when designs 2 and 3 are used.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck


