Deck 4: Elementary Number Theory and Methods of Proof
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/28
Play
Full screen (f)
Deck 4: Elementary Number Theory and Methods of Proof
1
Prove the following statement: For all real numbers x, 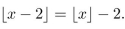
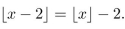

2
Prove the following statement: There is no smallest positive rational number.

3
Prove the following statement by contradiction: For all real numbers r and s, if r is rational
and s is irrational, then r + 2s is irrational.
and s is irrational, then r + 2s is irrational.

4
Outline a proof of the following statement by writing the "starting point" and the "conclusion
to be shown" in a proof of the statement.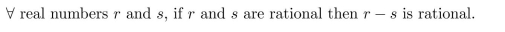
That is, complete the sentences below.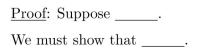
to be shown" in a proof of the statement.
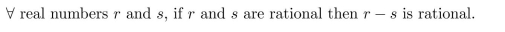
That is, complete the sentences below.
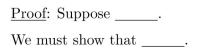

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
5
Is 605.83 a rational number? Justify your answer.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
6
Is 56.745 a rational number? Justify your answer.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the following statement: 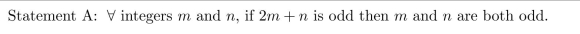
(a) Write a negation for Statement A.
(b) Disprove Statement A. That is, show that Statement A is false.
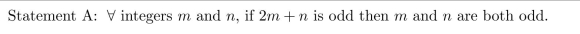
(a) Write a negation for Statement A.
(b) Disprove Statement A. That is, show that Statement A is false.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
8
Find a counterexample to show that the following statement is false: 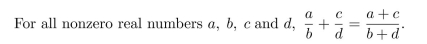
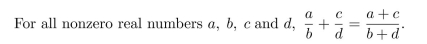

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
9
Prove the following statement: The sum of any two consecutive integers can be written in the
form 4n + 1 for some integer n.
form 4n + 1 for some integer n.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
10
Prove the statement below directly from the definitions of the terms. Do not use any other
facts previously proved in class or in the text or in the exercises.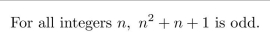
facts previously proved in class or in the text or in the exercises.
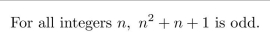

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
11
Show that the following statement is false: The product of any two irrational numbers is
irrational.
irrational.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
12
Is 0 divisible by 3? Justify your answer.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
13
State precisely (but concisely) what it means for an integer n to be odd.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
14
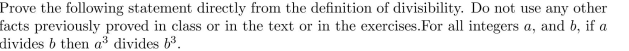

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
15
State precisely (but concisely) what it means for a number r to be rational.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
16
State precisely (but concisely) what it means for an integer n to be divisible by an integerd.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
17
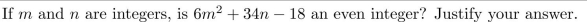

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
18
Prove the following statement directly from the definitions of the terms. Do not use any other
facts previously proved in class or in the text or in the exercises.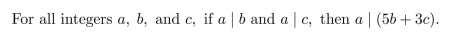
facts previously proved in class or in the text or in the exercises.
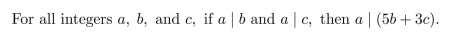

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
19
Does 12 divide 72? Justify your answer.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
20
Prove the following statement directly from the definitions of the terms. Do not use any other
facts previously proved in class or in the text or in the exercises.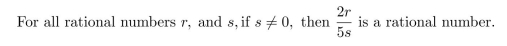
facts previously proved in class or in the text or in the exercises.
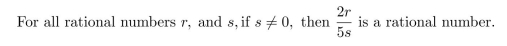

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the following statement: For all integers n, if n3 is odd then n is odd.
(a) Prove the statement either by contradiction or by contraposition. Clearly indicate which
method you are using.
(b) If you used proof by contradiction in part (a), write what you would "suppose" and
what you would "show" to prove the statement by contraposition. If you used proof by
contraposition in part (a), write what you would "suppose" and what you would "show"
to prove the statement by contradiction.
(a) Prove the statement either by contradiction or by contraposition. Clearly indicate which
method you are using.
(b) If you used proof by contradiction in part (a), write what you would "suppose" and
what you would "show" to prove the statement by contraposition. If you used proof by
contraposition in part (a), write what you would "suppose" and what you would "show"
to prove the statement by contradiction.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
22
True or false? For any irrational number r, r2 is irrational. Justify your answer.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the following statement: For all real numbers r, if r3 is irrational then r is irrational.
(a) Prove the statement either by contradiction or by contraposition. Clearly indicate which
method you are using.
(b) If you used proof by contradiction in part (a), write what you would "suppose" and
what you would "show" to prove the statement by contraposition. If you used proof by
contraposition in part (a), write what you would "suppose" and what you would "show"
to prove the statement by contradiction.
(a) Prove the statement either by contradiction or by contraposition. Clearly indicate which
method you are using.
(b) If you used proof by contradiction in part (a), write what you would "suppose" and
what you would "show" to prove the statement by contraposition. If you used proof by
contraposition in part (a), write what you would "suppose" and what you would "show"
to prove the statement by contradiction.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
24
Prove by contradiction that 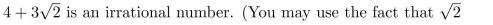
is irrational.)
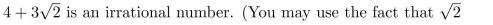
is irrational.)

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
25
Use the Euclidean algorithm to find the greatest common divisor of 284 and 168. Show your
work.
work.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
26


Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the following statement: For all integers n, if n3 is even then n is even.
(a) Prove the statement either by contradiction or by contraposition. Clearly indicate which
method you are using.
(b) If you used proof by contradiction in part (a), write what you would "suppose" and
what you would "show" to prove the statement by contraposition. If you used proof by
contraposition. in part (a), write what you would "suppose" and what you would "show"
to prove the statement by contradiction.
(a) Prove the statement either by contradiction or by contraposition. Clearly indicate which
method you are using.
(b) If you used proof by contradiction in part (a), write what you would "suppose" and
what you would "show" to prove the statement by contraposition. If you used proof by
contraposition. in part (a), write what you would "suppose" and what you would "show"
to prove the statement by contradiction.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
28
Use the Euclidean algorithm to calculate the greatest common divisor of 10,673 and 11,284.
Show your work.
Show your work.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck


