Deck 9: Counting and Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 9: Counting and Probability
1
A large pile of coins consists of pennies, nickels, dimes, and quarters (at least 20 of each).
(a) How many different collections of 20 coins can be chosen?
(b) How many different collections of 20 coins chosen at random will contain at least 3 coins
of each type?
(c) What is the probability that a collection of 20 coins chosen at random will contain at
least 3 coins of each type?
(a) How many different collections of 20 coins can be chosen?
(b) How many different collections of 20 coins chosen at random will contain at least 3 coins
of each type?
(c) What is the probability that a collection of 20 coins chosen at random will contain at
least 3 coins of each type?

2
In a certain discrete math class, three quizzes were given. Out of the 30 students in the class: 
(a) How many scored 12 or above on at least one quiz?
(b) How many scored 12 or above on quizzes 1 and 2 but not 3?

(a) How many scored 12 or above on at least one quiz?
(b) How many scored 12 or above on quizzes 1 and 2 but not 3?
 So 23 students scored 12 or above on at least one quiz.
So 23 students scored 12 or above on at least one quiz.b. The number of students who scored 12 or above on quizzes 1 and 2 but not 3 is 7 − 4 = 3.
3
The binomial theorem states that for any real numbers a and b, 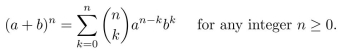
Use this theorem to compute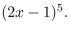
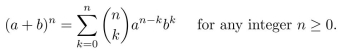
Use this theorem to compute
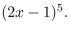
Apply the binomial theorem with a = 2x, b = −1, and n = 5.
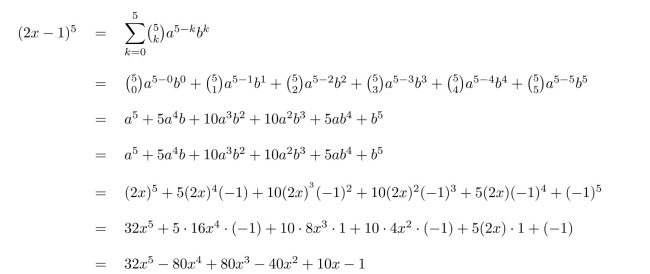
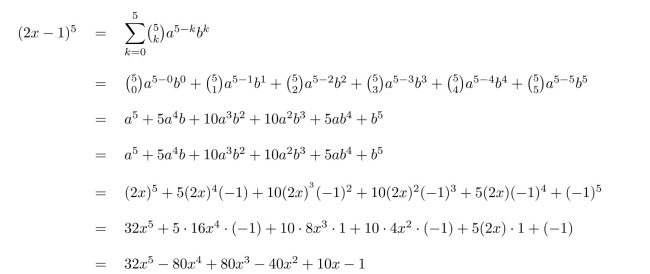
4
If six integers are chosen from the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, must there be at least two
integers with the property that the sum of the smaller plus the larger is 11? Why or why not?
Write an answer that would convince a good but skeptical fellow student who has learned the
statement of the pigeonhole principle but not seen an application like this one. Either describe
the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes, or describe a function
by giving its domain, co-domain, and how elements of the domain are related to elements of
the co-domain.
integers with the property that the sum of the smaller plus the larger is 11? Why or why not?
Write an answer that would convince a good but skeptical fellow student who has learned the
statement of the pigeonhole principle but not seen an application like this one. Either describe
the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes, or describe a function
by giving its domain, co-domain, and how elements of the domain are related to elements of
the co-domain.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose there are three routes from Byrne Hall to McGaw Hall and five routes from McGaw
Hall to Monroe Hall. How many ways is it possible to travel from Byrne Hall to Monroe Hall
by way of McGaw Hall?
Hall to Monroe Hall. How many ways is it possible to travel from Byrne Hall to Monroe Hall
by way of McGaw Hall?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
Let T be the set {3, 4, 5, 6, 7, 8, 9, 10} and suppose five integers are chosen from T. Must two
of these integers have the property that the difference of the larger minus the smaller equals
2? Why or why not? Write an answer that would convince a good but skeptical fellow student
who has learned the statement of the pigeonhole principle but not seen an application like this
one. Either describe the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes,
or describe a function by giving its domain, co-domain, and how elements of the domain are
related to elements of the co-domain.
of these integers have the property that the difference of the larger minus the smaller equals
2? Why or why not? Write an answer that would convince a good but skeptical fellow student
who has learned the statement of the pigeonhole principle but not seen an application like this
one. Either describe the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes,
or describe a function by giving its domain, co-domain, and how elements of the domain are
related to elements of the co-domain.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
The binomial theorem states that for any real numbers a and b, 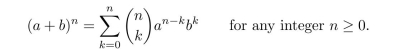
Use this theorem to show that for any integer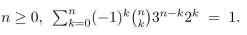
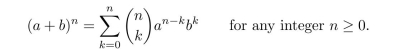
Use this theorem to show that for any integer
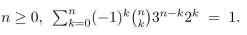

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
How many elements are in the one-dimensional array shown below? 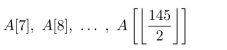
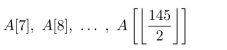

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
Given any set of 30 integers, must there be two that have the same remainder when they are
divided by 25? Write an answer that would convince a good but skeptical fellow student who
has learned the statement of the pigeonhole principle but not seen an application like this
one. Either describe the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes,
or describe a function by giving its domain, co-domain, and how elements of the domain are
related to elements of the co-domain.
divided by 25? Write an answer that would convince a good but skeptical fellow student who
has learned the statement of the pigeonhole principle but not seen an application like this
one. Either describe the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes,
or describe a function by giving its domain, co-domain, and how elements of the domain are
related to elements of the co-domain.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
10
A club has seven members. Three are to be chosen to go as a group to a national meeting.
(a) How many distinct groups of three can be chosen?
(b) If the club contains four men and three women, how many distinct groups of three contain
two men and one woman?
(c) If the club contains four men and three women, how many distinct groups of three contain
at most two men?
(d) If the club contains four men and three women, how many distinct groups of three contain
at least one woman?
(e) If the club contains four men and three women, what is the probability that a distinct
group of three will contain at least one woman?
(f) If two members of the club refuse to travel together as part of the group (but each is
willing to go if the other does not), how many distinct groups of three can be chosen?
(g) If two members of the club insists on either traveling together or not going at all, How
many distinct groups of three can be chosen?
(a) How many distinct groups of three can be chosen?
(b) If the club contains four men and three women, how many distinct groups of three contain
two men and one woman?
(c) If the club contains four men and three women, how many distinct groups of three contain
at most two men?
(d) If the club contains four men and three women, how many distinct groups of three contain
at least one woman?
(e) If the club contains four men and three women, what is the probability that a distinct
group of three will contain at least one woman?
(f) If two members of the club refuse to travel together as part of the group (but each is
willing to go if the other does not), how many distinct groups of three can be chosen?
(g) If two members of the club insists on either traveling together or not going at all, How
many distinct groups of three can be chosen?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose that a fair coin is tossed ten times.
(a) How many ways can at least eight heads be obtained?
(b) What is the probability of obtaining at least eight heads?
(a) How many ways can at least eight heads be obtained?
(b) What is the probability of obtaining at least eight heads?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
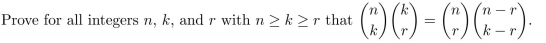

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13
Given any set of 15 integers, must there be two that have the same remainder when divided by
12? Write an answer that would convince a good but skeptical fellow student who has learned
the statement of the pigeonhole principle but not seen an application like this one. Either
describe the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes, or describe
a function by giving its domain, co-domain, and how elements of the domain are related to
elements of the co-domain.
12? Write an answer that would convince a good but skeptical fellow student who has learned
the statement of the pigeonhole principle but not seen an application like this one. Either
describe the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes, or describe
a function by giving its domain, co-domain, and how elements of the domain are related to
elements of the co-domain.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
On each of three consecutive days the National Weather Service announces that there is a 50-50
chance of rain. Assuming that the National Weather Service is correct, what is the probability
that it rains on at most one of the three days? Justify your answer. (Hint: Represent the
outcome that it rains on day 1 and doesn't rain on days 2 and 3 as RNN.)
chance of rain. Assuming that the National Weather Service is correct, what is the probability
that it rains on at most one of the three days? Justify your answer. (Hint: Represent the
outcome that it rains on day 1 and doesn't rain on days 2 and 3 as RNN.)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
In a certain state, license plates each consist of 2 letters followed by 3 digits.
(a) How many different license plates are there?
(b) How many different license plates are there that have no repeated letters or digits?
(a) How many different license plates are there?
(b) How many different license plates are there that have no repeated letters or digits?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
If five integers are chosen from the set {1, 2, 3, 4, 5, 6, 7, 8}, must there be at least two integers
with the property that the larger minus the smaller is 2? Write an answer that would convince
a good but skeptical fellow student who has learned the statement of the pigeonhole principle
but not seen an application like this one. Either describe the pigeons, the pigeonholes, and
how the pigeons get to the pigeonholes, or describe a function by giving its domain, co-domain,
and how elements of the domain are related to elements of the co-domain.
with the property that the larger minus the smaller is 2? Write an answer that would convince
a good but skeptical fellow student who has learned the statement of the pigeonhole principle
but not seen an application like this one. Either describe the pigeons, the pigeonholes, and
how the pigeons get to the pigeonholes, or describe a function by giving its domain, co-domain,
and how elements of the domain are related to elements of the co-domain.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
Express the following sum in closed form (without using a summation symbol and without
using an ellipsis . . . ):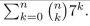
using an ellipsis . . . ):
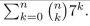

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
In a certain state, license plates each consist of 2 letters followed by either 3 or 4 digits. How
many different license plates are there that have no repeated letters or digits?
many different license plates are there that have no repeated letters or digits?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
A screening test for a certain disease is used in a large population of people of whom 1 in 1000
actually have the disease. Suppose that the false positive rate is 1% and the false negative
rate is 0.5%. Thus a person who has the disease tests positive for it 99.5% of the time, and a
person who does not have the disease tests negative for it 99% of the time.
(a) What is the probability that a randomly chosen person who tests positive for the disease
actually has the disease?
(b) What is the probability that a randomly chosen person who tests negative for the disease
actually has the disease?
actually have the disease. Suppose that the false positive rate is 1% and the false negative
rate is 0.5%. Thus a person who has the disease tests positive for it 99.5% of the time, and a
person who does not have the disease tests negative for it 99% of the time.
(a) What is the probability that a randomly chosen person who tests positive for the disease
actually has the disease?
(b) What is the probability that a randomly chosen person who tests negative for the disease
actually has the disease?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
22
A teacher offers ten possible assignments for extra credit in a course but requires students to
choose them, without looking, from a hat. Six assignments involve library research and four
are computer programming exercises. Suppose that a student chooses two assignments, one
after the other, at random without replacement.
(a) What is the probability that both assignments are computer programming exercises?
(b) What is the probability that at least one of the assignments is a computer programming
exercise?
choose them, without looking, from a hat. Six assignments involve library research and four
are computer programming exercises. Suppose that a student chooses two assignments, one
after the other, at random without replacement.
(a) What is the probability that both assignments are computer programming exercises?
(b) What is the probability that at least one of the assignments is a computer programming
exercise?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
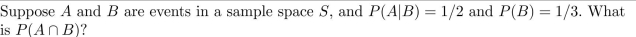

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
A coin is loaded so that the probability of heads is 0.55 and the probability of tails is 0.45.
Suppose the coin is tossed twice and the results of the tosses are independent.
(a) What is the probability of obtaining exactly two heads?
(b) What is the probability of obtaining exactly one head?
(c) What is the probability of obtaining no heads?
(d) What is the probability of obtaining at least one head?
Suppose the coin is tossed twice and the results of the tosses are independent.
(a) What is the probability of obtaining exactly two heads?
(b) What is the probability of obtaining exactly one head?
(c) What is the probability of obtaining no heads?
(d) What is the probability of obtaining at least one head?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
An urn contains four balls numbered 1, 3, 4, and 6. If a person selects a set of two balls at
random, what is the expected value of the product of the numbers on the balls?
random, what is the expected value of the product of the numbers on the balls?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck


