Deck 1: The Foundations: Logic and Proofs
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/18
Play
Full screen (f)
Deck 1: The Foundations: Logic and Proofs
1
Prove each of the following statements. (a) The sum of two even integers is always even. (b) The sum of an even integer and an odd integer is always odd.
(a) Suppose that m and n are even integers. Then there are integers j and k such that m=2 j and n=2 k. It follows that m+n=2 j+2 k=2(j+k)=2 l, where l=j+k. Hence m+n is even.
(b) Suppose that m is even and n is odd. Then there are integers j and k such that such that m=2 j and n=2 k+1. It follows that m+n=2 j+(2 k+1)=2(j+k)+1=2 l+1, where l=j+k. Hence m+n is odd.
(b) Suppose that m is even and n is odd. Then there are integers j and k such that such that m=2 j and n=2 k+1. It follows that m+n=2 j+(2 k+1)=2(j+k)+1=2 l+1, where l=j+k. Hence m+n is odd.
2
Prove or disprove that (p → q) → r and p → (q →r) are equivalent.
Suppose that p is false, q is true, and r is false. Then (p → q) → r is false since its premise p→ q is true while its conclusion r is false. On the other hand, p →(q →r) is true in this situation since its premise p is false. Therefore (p→ q) → r and p →(q → r) are not equivalent.
3
Write the converse and contrapositive of the statement "If it is sunny, then I will go swimming."
The converse of the statement is "If I go swimming, then it is sunny." The contrapositive of the statement is "If I do not go swimming, then it is not sunny."
4
Prove that there are no solutions in positive integers to the equation x4 + y4 = 100.

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
5
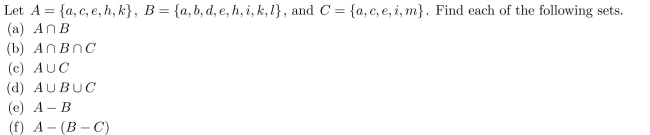

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
6
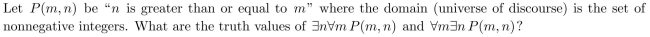

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
7
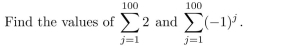

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
8
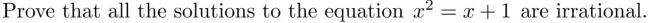

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
9
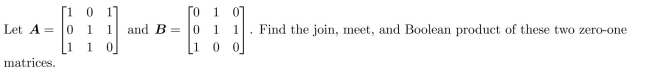

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
10
Show that ¬(p ∨ ¬q) and q ∧ ¬p are equivalent (a) using a truth table. (b) using logical equivalences.

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose that Q(x) is the statement "x + 1 = 2x." What are the truth values of ∀x Q(x) and ∃x Q(x)?

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
12
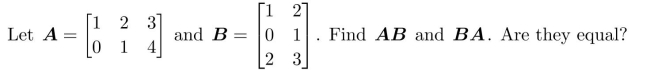

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
13


Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
14
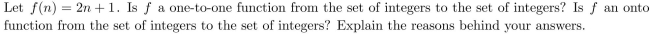

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
15
What is the truth value of (p ∨ q) → (p ∧ q) when both p and q are false?

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
16


Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
17
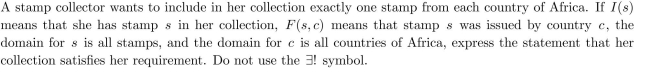

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
18
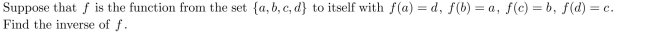

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck


