Deck 8: Advanced Counting Techniques
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/16
Play
Full screen (f)
Deck 8: Advanced Counting Techniques
1
List the derangements of the set {1, 2, 3, 4}.
The derangements of {1, 2, 3, 4} are the permutations of these four integers that leave no integer in its original position. These are 2143, 2341, 2413, 3142, 3412, 3421, 4123, 4312, and 4321.
2
Use generating functions to solve the recurrence relation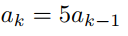 =1,2,3, ... , with initial condition
=1,2,3, ... , with initial condition
a0=3
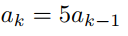 =1,2,3, ... , with initial condition
=1,2,3, ... , with initial conditiona0=3
Let 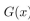 be the generating function for the sequence https://storage.examlex.com/TB34225555/
be the generating function for the sequence https://storage.examlex.com/TB34225555/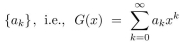 . Then
. Then 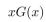 =
=
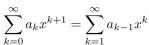 ,It follows that:
,It follows that: 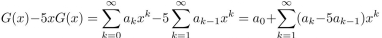 =3, because of the given recurrence relation and initial condition. Thus
=3, because of the given recurrence relation and initial condition. Thus 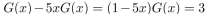 ,so
,so
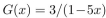 it follows from an identity in table 1 of section 8.4 that
it follows from an identity in table 1 of section 8.4 that 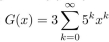 . consecuently
. consecuently 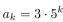 .
.
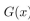 be the generating function for the sequence https://storage.examlex.com/TB34225555/
be the generating function for the sequence https://storage.examlex.com/TB34225555/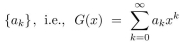 . Then
. Then 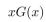 =
=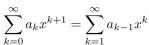 ,It follows that:
,It follows that: 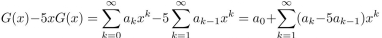 =3, because of the given recurrence relation and initial condition. Thus
=3, because of the given recurrence relation and initial condition. Thus 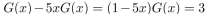 ,so
,so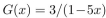 it follows from an identity in table 1 of section 8.4 that
it follows from an identity in table 1 of section 8.4 that 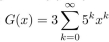 . consecuently
. consecuently 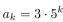 .
. 3
Suppose that f(n) satisfies the divide-and-conquer relation 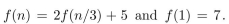 What is f(81)?
What is f(81)?
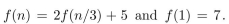 What is f(81)?
What is f(81)?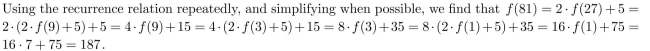
4
Find the solution of the recurrence relation 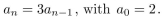
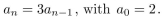

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
5
How many positive integers not exceeding 1000 are not divisible by 4, 6, or 9?

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
6
How many onto functions are there from a set with six elements to a set with four elements?

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose that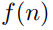 satisfies the divide-and-conquer recurrence relation
satisfies the divide-and-conquer recurrence relation 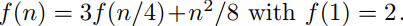 What is
What is 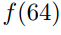 ?
?
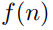 satisfies the divide-and-conquer recurrence relation
satisfies the divide-and-conquer recurrence relation 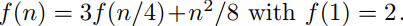 What is
What is 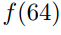 ?
?
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
8
How many ways are there to assign six jobs to four employees so that every employee is assigned at least one job?

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose that 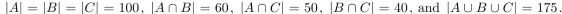
How many elements are in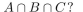
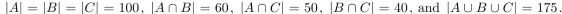
How many elements are in
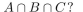

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
10
Find a generating function for the sequence 2, 3, 4, 5, . . ..

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
11
How many permutations are there of the digits in the string 12345 that leave 3 fixed but leave no other integer fixed? (For instance, 24351 is such a permutation.)

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
12
Find a recurrence relation and initial condition for the number of fruit flies in a jar if there are 12 flies initially and every week there are six times as many flies in the jar as there were the previous week.

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
13
(a) Find a recurrence relation for the number of ways to climb n stairs if stairs can be climbed two or three at a time. (b) What are the initial conditions? (c) How many ways are there to climb eight stairs?

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
14
What is the solution to the recurrence relation 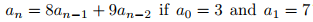
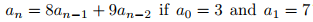

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
15
How many positive integers not exceeding 1000 are not divisible by either 4 or 6?

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
16
Find the solution of the linear homogeneous recurrence relation 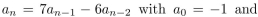 a1 = 4.
a1 = 4.
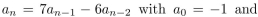 a1 = 4.
a1 = 4.
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck


