Deck 9: Relations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/13
Play
Full screen (f)
Deck 9: Relations
1
Show that the inclusion relation, 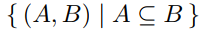 , is a partial ordering on the set of all subsets of
, is a partial ordering on the set of all subsets of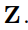
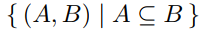 , is a partial ordering on the set of all subsets of
, is a partial ordering on the set of all subsets of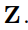
We see that set inclusion is reflexive since A 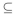 A whenever A is a subset of
A whenever A is a subset of 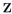 . Since A
. Since A 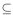 B and B
B and B 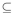 A imply that A=B whenever A and B are subsets of
A imply that A=B whenever A and B are subsets of 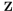 , we see that set inclusion is antisymmetric. Now suppose that A
, we see that set inclusion is antisymmetric. Now suppose that A 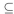 B and B
B and B 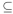 C where A, B , and C are subsets of
C where A, B , and C are subsets of 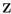 Then A
Then A  C , so set inclusion is transitive.
C , so set inclusion is transitive.
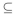 A whenever A is a subset of
A whenever A is a subset of 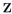 . Since A
. Since A 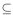 B and B
B and B 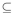 A imply that A=B whenever A and B are subsets of
A imply that A=B whenever A and B are subsets of 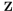 , we see that set inclusion is antisymmetric. Now suppose that A
, we see that set inclusion is antisymmetric. Now suppose that A 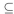 B and B
B and B 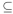 C where A, B , and C are subsets of
C where A, B , and C are subsets of 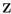 Then A
Then A  C , so set inclusion is transitive.
C , so set inclusion is transitive. 2
Show that the relation 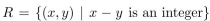 is an equivalence relation on the set of rational numbers. What are the equivalence classes of 0 and 12 ?
is an equivalence relation on the set of rational numbers. What are the equivalence classes of 0 and 12 ?
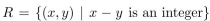 is an equivalence relation on the set of rational numbers. What are the equivalence classes of 0 and 12 ?
is an equivalence relation on the set of rational numbers. What are the equivalence classes of 0 and 12 ?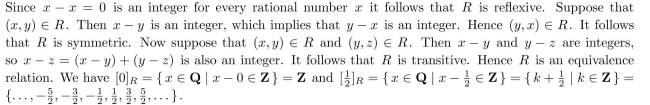
3
Consider the poset with the following Hasse diagram. 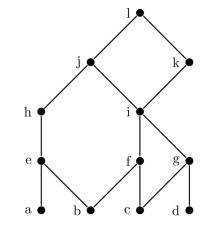 (a) Find all maximal elements of the poset. (b) Find all minimal elements of the poset. (c) Find the least element of the poset if it exists, or show that it does not exist. (d) Find the greatest element of the poset if it exists, or show that it does not exist. (e) What is the greatest lower bound of the set {a, b, c}? (f) What is the least upper bound of the set {a, b, c}?
(a) Find all maximal elements of the poset. (b) Find all minimal elements of the poset. (c) Find the least element of the poset if it exists, or show that it does not exist. (d) Find the greatest element of the poset if it exists, or show that it does not exist. (e) What is the greatest lower bound of the set {a, b, c}? (f) What is the least upper bound of the set {a, b, c}?
 (a) Find all maximal elements of the poset. (b) Find all minimal elements of the poset. (c) Find the least element of the poset if it exists, or show that it does not exist. (d) Find the greatest element of the poset if it exists, or show that it does not exist. (e) What is the greatest lower bound of the set {a, b, c}? (f) What is the least upper bound of the set {a, b, c}?
(a) Find all maximal elements of the poset. (b) Find all minimal elements of the poset. (c) Find the least element of the poset if it exists, or show that it does not exist. (d) Find the greatest element of the poset if it exists, or show that it does not exist. (e) What is the greatest lower bound of the set {a, b, c}? (f) What is the least upper bound of the set {a, b, c}?
4
What is the transitive closure of the relation in problem 3?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
5
Which ordered pairs are in the relation { (x, y) | x > y + 1 } on the set {1, 2, 3, 4}?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose that R1 and R2 are symmetric relations on a set A. Prove or disprove that R1 − R2 is also symmetric.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
7
Find the reflexive closure and the symmetric closure of the relation {(1,2),(1,4),(2,3),(3,1),(4,2)} on the set {1,2,3,4} .

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
8
(a) Show that the relation 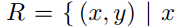 and
and 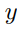 are bit strings containing the same number of 0s } is an equivalence relation.
are bit strings containing the same number of 0s } is an equivalence relation.
(b) What are the equivalence classes of the bit strings 1, 00, and 101 under the relation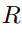 ?
?
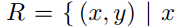 and
and 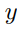 are bit strings containing the same number of 0s } is an equivalence relation.
are bit strings containing the same number of 0s } is an equivalence relation.(b) What are the equivalence classes of the bit strings 1, 00, and 101 under the relation
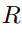 ?
?
Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
9
What is the join of the 3-ary relation {(Lewis, MS410, N507), (Rosen, CS540, N525), (Smith, CS518, N504), (Smith, MS410, N510)} and the 4-ary {(MS410, N507,Monday, 6: 00), (MS410, N507, Wednesday, 6: 00), (CS540, N525, Monday, 7: 30), (CS518, N504, Tuesday, 6: 00), (CS518, N504, Thursday, 6: 00)} with respect to the last two fields of the first relation and the first two fields of the second relation?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
10
(a) Are the sets {1,3,6},{2,4,7} , and {5} a partition of {1,2,3,4,5,6,7} ?
(b) Are the sets {1,2,4,5},{3,6,7} , and {2,3} a partition of {1,2,3,4,5,6,7} ?
(b) Are the sets {1,2,4,5},{3,6,7} , and {2,3} a partition of {1,2,3,4,5,6,7} ?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
11
What are the minimal and maximal elements in the poset with the following Hasse diagram? Are there least

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the following relations on the set of positive integers. 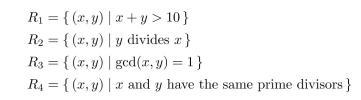 (a) Which of these relations are reflexive? Justify your answers. (b) Which of these relations are symmetric? Justify your answers. (c) Which of these relations are antisymmetric? Justify your answers. (d) Which of these relations are transitive? Justify your answers.
(a) Which of these relations are reflexive? Justify your answers. (b) Which of these relations are symmetric? Justify your answers. (c) Which of these relations are antisymmetric? Justify your answers. (d) Which of these relations are transitive? Justify your answers.
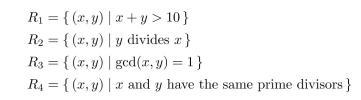 (a) Which of these relations are reflexive? Justify your answers. (b) Which of these relations are symmetric? Justify your answers. (c) Which of these relations are antisymmetric? Justify your answers. (d) Which of these relations are transitive? Justify your answers.
(a) Which of these relations are reflexive? Justify your answers. (b) Which of these relations are symmetric? Justify your answers. (c) Which of these relations are antisymmetric? Justify your answers. (d) Which of these relations are transitive? Justify your answers.
Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
13

b) and (b,
c) with
a = b and b = c. R1 is not transitive since (3, 1) and (1, 3) belong to R1 but (3, 3) is not in R1. R3
is not transitive since (1, 2) and (2, 1) belong to R3 but (1, 1) does not belong to R3.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck


