Deck 1: A: the Foundations: Logic and Proofs
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/201
Play
Full screen (f)
Deck 1: A: the Foundations: Logic and Proofs
1
What is the negation of the propositions
4.5 + 2.5 = 6
4.5 + 2.5 = 6

2
determine whether the proposition is TRUE or FALSE.
If it is raining, then it is raining.
If it is raining, then it is raining.
True
3
Write the truth table for the proposition 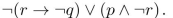
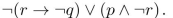
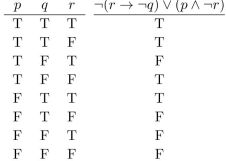
4
Find a proposition with three variables 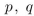 , and
, and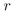 , that is true when at most one of the three variables is true, and false otherwise.
, that is true when at most one of the three variables is true, and false otherwise.
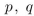 , and
, and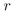 , that is true when at most one of the three variables is true, and false otherwise.
, that is true when at most one of the three variables is true, and false otherwise.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
5
determine whether the proposition is TRUE or FALSE.
If 1 + 1 = 2 or 1 + 1 = 3, then 2 + 2 = 3 and 2 + 2 = 4.
If 1 + 1 = 2 or 1 + 1 = 3, then 2 + 2 = 3 and 2 + 2 = 4.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
6
Find a proposition with three variables 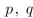 , and
, and 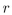 that is true when
that is true when 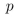 and
and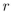 are true and
are true and 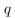 is false, and false otherwise.
is false, and false otherwise.
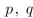 , and
, and 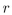 that is true when
that is true when 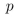 and
and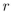 are true and
are true and 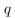 is false, and false otherwise.
is false, and false otherwise.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
7
Find a proposition with three variables 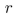 , and
, and 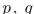 that is never true.
that is never true.
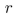 , and
, and 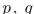 that is never true.
that is never true.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
8
use the conditional-disjunction equivalence to find an equivalent compound proposition that does not
involve conditions.
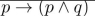
involve conditions.
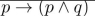

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
9
use the conditional-disjunction equivalence to find an equivalent compound proposition that does not
involve conditions.
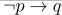
involve conditions.
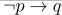

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
10
Determine whether 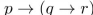 and
and 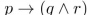 are equivalent.
are equivalent.
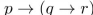 and
and 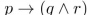 are equivalent.
are equivalent.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
11
(a) Find a proposition with the truth table at the right.
(b) Find a proposition using only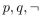 , and the connective
, and the connective  that has this truth table.
that has this truth table.
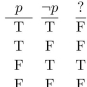
(b) Find a proposition using only
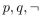 , and the connective
, and the connective 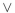 that has this truth table.
that has this truth table.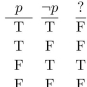

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
12
determine whether the proposition is TRUE or FALSE.
1 + 1 = 3 if and only if 2 + 2 = 3.
1 + 1 = 3 if and only if 2 + 2 = 3.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
13
Find a proposition using only 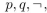 , and the connective
, and the connective 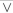 with the truth table at the right.
with the truth table at the right. 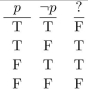
 , and the connective
, and the connective  with the truth table at the right.
with the truth table at the right. 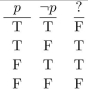

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
14
Determine whether 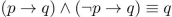 .
.
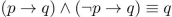 .
.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
15
What is the negation of the propositions
Alissa owns more quilts than Federico.
Alissa owns more quilts than Federico.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
16
determine whether the proposition is TRUE or FALSE.
If 2 + 1 = 3, then 2 = 3 − 1.
If 2 + 1 = 3, then 2 = 3 − 1.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
17
Determine whether 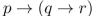 is equivalent to
is equivalent to 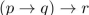
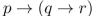 is equivalent to
is equivalent to 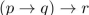

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
18
What is the negation of the propositions
Abby has more than 300 friends on Facebook.
Abby has more than 300 friends on Facebook.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
19
determine whether the proposition is TRUE or FALSE.
If 1 < 0, then 3 = 4.
If 1 < 0, then 3 = 4.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
20
What is the negation of the propositions
A messaging package for a cell phone costs less than $20 per month.
A messaging package for a cell phone costs less than $20 per month.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
21
Prove that 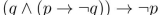 is a tautology using propositional equivalence and the laws of logic.
is a tautology using propositional equivalence and the laws of logic.
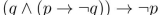 is a tautology using propositional equivalence and the laws of logic.
is a tautology using propositional equivalence and the laws of logic.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
22
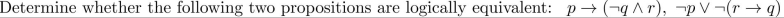

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
23
Write a proposition equivalent to 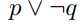 that uses only
that uses only  , and the connective
, and the connective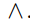
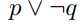 that uses only
that uses only 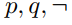 , and the connective
, and the connective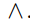

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
24
Determine whether this proposition is a tautology: 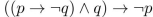
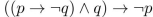

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
25
Prove that ¬p → ¬q and its inverse are not logically equivalent.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
26
write the statement in the form "If . . . , then . . . ."
The team wins if the quarterback can pass.
The team wins if the quarterback can pass.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
27
Determine whether this proposition is a tautology: 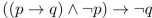
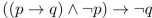

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
28
write the statement in the form "If . . . , then . . . ."
It is hot whenever it is sunny.
It is hot whenever it is sunny.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
29
Write a proposition equivalent to 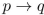 using only
using only 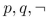 , and the connectivehttps://storage.examlex.com/TB34225555/
, and the connectivehttps://storage.examlex.com/TB34225555/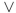 .
.
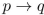 using only
using only 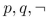 , and the connectivehttps://storage.examlex.com/TB34225555/
, and the connectivehttps://storage.examlex.com/TB34225555/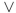 .
.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
30
write the statement in the form "If . . . , then . . . ."
x is even only if y is odd.
x is even only if y is odd.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
31
write the statement in the form "If . . . , then . . . ."
A implies B.
A implies B.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
32
Prove that the proposition "if it is not hot, then it is hot" is equivalent to "it is hot."

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
33
write the statement in the form "If . . . , then . . . ."
You need to be registered in order to check out library books.
You need to be registered in order to check out library books.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
34
Write the contrapositive, converse, and inverse of the following: You sleep late if it is Saturday.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
35
Determine whether the following two propositions are logically equivalent: https://storage.examlex.com/TB34225555/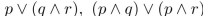 .
.
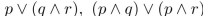 .
.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
36
Write the contrapositive, converse, and inverse of the following: If you try hard, then you will win.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
37
write the statement in the form "If . . . , then . . . ."
To get a good grade it is necessary that you study.
To get a good grade it is necessary that you study.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
38
write the statement in the form "If . . . , then . . . ."
Studying is sufficient for passing.
Studying is sufficient for passing.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
39
Write a proposition equivalent to 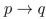 using only
using only 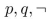 , and the connective https://storage.examlex.com/TB34225555/
, and the connective https://storage.examlex.com/TB34225555/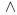 .
.
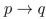 using only
using only 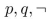 , and the connective https://storage.examlex.com/TB34225555/
, and the connective https://storage.examlex.com/TB34225555/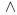 .
.
Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
40
Prove that p → q and its converse are not logically equivalent.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
41
Express r ⊕ d in English, where r is "it is rainy" and d is "it is dry."

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
42
A says "I am not a knight," B says "I am not a spy," and C says "I am not a knave."

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
43
A set of propositions is consistent if there is an assignment of truth values to each of the variables in the propositions that makes each proposition true. Is the following set of propositions consistent? The system is in multiuser state if and only if it is operating normally. If the system is operating normally, the kernel is functioning. The kernel is not functioning or the system is in interrupt mode. If the system is not in multiuser state, then it is in interrupt mode. The system is in interrupt mode.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
44
On the island of knights and knaves you encounter two people, A and B. Person A says "B is a knave." Person B says "At least one of us is a knight." Determine whether each person is a knight or a knave. Questions 56-58 relate to inhabitants of an island on which there are three kinds of people: knights who always tell the truth, knaves who always lie, and spies who can either tell the truth or lie. You encounter three people, A, B, and C . You know one of the three people is a knight, one is a knave, and one is a spy. Each of the three people knows the type of person each of the other two is. For each of these situations, if possible, determine whether there is a unique solution, list all possible solutions or state that there are no solutions.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
45
Using c for "it is cold" and d for "it is dry," write "It is neither cold nor dry" in symbols.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
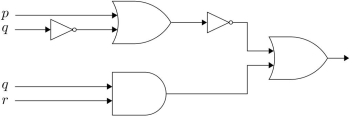
46
Find the output of the combinatorial circuits


Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
47
A says "I am a spy," B says "I am a spy" and C says "B is a spy."

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
48
write the negation of the statement. (Don't write "It is not true that . . . .")
I will go to the play or read a book, but not both.
I will go to the play or read a book, but not both.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
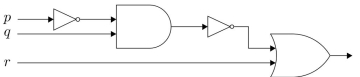
49
Find the output of the combinatorial circuits


Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
50
write the negation of the statement. (Don't write "It is not true that . . . .")
It is Thursday and it is cold.
It is Thursday and it is cold.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
51
On the island of knights and knaves you encounter two people, A and B. Person A says "B is a knave." Person B says "We are both knights." Determine whether each person is a knight or a knave.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
52
Translate the given statement into propositional logic using the propositions provided: On certain highways in the Washington, DC metro area you are allowed to travel on high occupancy lanes during rush hour only if there are at least three passengers in the vehicle. Express your answer in terms of r:"You are traveling during rush hour." t:"You are riding in a car with at least three passengers." and h:"You can travel on a high occupancy lane."

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
53
Using c for "it is cold" and w for "it is windy," write "To be windy it is necessary that it be cold" in symbols.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
54
Using c for "it is cold" and r for "it is rainy," write "It is rainy if it is not cold" in symbols.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
55
write the negation of the statement. (Don't write "It is not true that . . . .")
If it is rainy, then we go to the movies.
If it is rainy, then we go to the movies.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
56
A says "I am a knight," B says "I am a knave," and C says "I am not a knave."

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
57
Explain why the negation of "Al and Bill are absent" is not "Al and Bill are present."

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
58
Using c for "it is cold," r for "it is rainy," and w for "it is windy," write "It is rainy only if it is windy and cold" in symbols.

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
59
Construct a combinatorial circuit using inverters, OR gates, and AND gates, that produces the outputs
from input bits p, q and r.
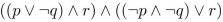
from input bits p, q and r.
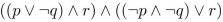

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
60
Construct a combinatorial circuit using inverters, OR gates, and AND gates, that produces the outputs
from input bits p, q and r.
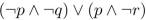
from input bits p, q and r.
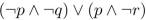

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
61
suppose that Q(x) is "x + 1 = 2x," where x is a real number. Find the truth value of the statement.
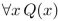
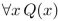

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
62
suppose P(x, y) is a predicate and the universe for the variables x and y is {1, 2, 3}. Suppose
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
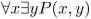
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
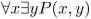

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
63
P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement.
P(1, −1)
P(1, −1)

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
64
P(m, n) means "m ≤ n," where the universe of discourse for m and n is the set of nonnegative integers.
What is the truth value of the statement?
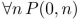
What is the truth value of the statement?
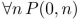

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
65
P(x, y) means "x and y are real numbers such that x + 2y = 5." Determine whether the statement is true.
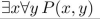
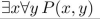

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
66
P(m, n) means "m ≤ n," where the universe of discourse for m and n is the set of nonnegative integers.
What is the truth value of the statement?
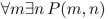
What is the truth value of the statement?
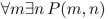

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
67
express the negation of the statement in terms of quantifiers without using the negation symbol.
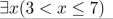
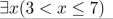

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
68
suppose that Q(x) is "x + 1 = 2x," where x is a real number. Find the truth value of the statement.
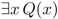
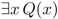

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
69
suppose that Q(x) is "x + 1 = 2x," where x is a real number. Find the truth value of the statement.
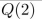
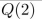

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
70
express the negation of the statement in terms of quantifiers without using the negation symbol.
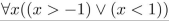
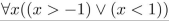

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
71
P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement.
P(0, 0)
P(0, 0)

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
72
P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement.
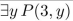
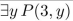

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
73
P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement.
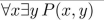
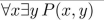

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
74
P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement.
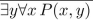
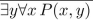

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
75
P(x, y) means "x and y are real numbers such that x + 2y = 5." Determine whether the statement is true.
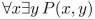
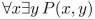

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
76
P(m, n) means "m ≤ n," where the universe of discourse for m and n is the set of nonnegative integers.
What is the truth value of the statement?
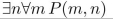
What is the truth value of the statement?
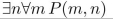

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
77
P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement.
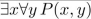
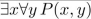

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
78
Determine whether the compound propositions are satisfiable.
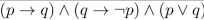
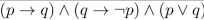

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
79
Determine whether the compound propositions are satisfiable.
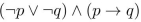
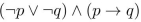

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck
80
P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement.
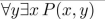
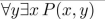

Unlock Deck
Unlock for access to all 201 flashcards in this deck.
Unlock Deck
k this deck


