Deck 8: Sequences, Induction, and Probability

Question 1

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = 3 n - 3$$

A) $0,3,6,9$
B) $0,1,2,3$
C) $6,9,12,15$
D) $0 , - 3 , - 6 , - 9$

Answer 1

A

Question 2

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = ( - 1 ) ^ { n + 1 } ( n + 4 )$$

A) $5 , - 6,7 , - 8$
B) $- 5,6 , - 7,8$
C) $5 , - 12,21 , - 32$
D) $- 6,7 , - 8,9$

Answer 2

A

Question 3

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \frac { 5 } { n ^ { 2 } }$$

A) $5 , \frac { 5 } { 4 } , \frac { 5 } { 9 } , \frac { 5 } { 16 }$
B) $1 , \frac { 2 } { 4 } , \frac { 3 } { 9 } , \frac { 4 } { 16 }$
C) $\frac { 5 } { 4 } , \frac { 5 } { 9 } , \frac { 5 } { 16 } , \frac { 5 } { 25 }$
D) $1 , \frac { 1 } { 4 } , \frac { 1 } { 9 } , \frac { 1 } { 16 }$

Answer 3

A

Question 4

Write the first four terms of the sequence whose general term is given.
$$\mathrm { a } _ { \mathrm { n } } = 4 ( 2 \mathrm { n } - 1 )$$

A) $4,12,20,28$
B) $1,3,5,7$
C) $- 4,4,12,20$
D) $4,8,12,16$

Question 5

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = 4 ^ { n }$$

A) $4,16,64,256$
B) $1,16,81,256$
C) $1,4,16,64$
D) $16,64,256,1024$

Question 6

Use Recursion Formulas
$a _ { 1 } = - 5$ and $a _ { n } = - 4 a _ { n - 1 }$ for $n \geq 2$

A) $- 5,20 , - 80,320$
B) $5 , - 20,80 , - 320$
C) $- 5 , - 20 , - 80 , - 320$
D) $- 5,22 , - 82,322$

Question 7

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = 6 n$$

A) $6,12,18,24$
B) $0,6,12,18$
C) $7,8,9,10$
D) $5,4,3,2$

Question 8

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \left( - \frac { 1 } { 4 } \right) ^ { n }$$

A) $- \frac { 1 } { 4 } , \frac { 1 } { 16 } , - \frac { 1 } { 64 } , \frac { 1 } { 256 }$
B) $- \frac { 1 } { 4 } , - \frac { 1 } { 16 } , - \frac { 1 } { 64 } , - \frac { 1 } { 256 }$
$\mathrm { C } ) - \frac { 1 } { 4 } , \frac { 1 } { 8 } , - \frac { 1 } { 12 } , - \frac { 1 } { 16 }$
D) $\frac { 1 } { 4 } , - \frac { 1 } { 8 } , \frac { 1 } { 12 } , - \frac { 1 } { 16 }$

Question 9

Use Recursion Formulas
$a _ { 1 } = 4$ and $a _ { n } = a _ { n - 1 } - 3$ for $n \geq 2$

A) $4,1 , - 2 , - 5$
B) $- 3 , - 6 , - 9 , - 12$
C) $4,7,10,13$
D) $4,3,0 , - 3$

Question 10

Solve the problem.
A deposit of $9000 is made in an account that earns 8% interest compounded quarterly. The balance in the account after n quarters is given by the sequence $a _ { n } = 9000 \left( 1 + \frac { 0.08 } { 4 } \right) ^ { n } \quad n = 1,2,3 , \ldots$
Find the balance in the account after 28 quarters.

A) $\$ 15,669.22$
B) $\$ 15,762.22$
C) $\$ 15,721.22$
D) $\$ 15,524.22$

Question 11

Use Recursion Formulas
$a _ { 1 } = 5$ and $a _ { n } = 3 a _ { n - 1 }$ for $n \geq 2$

A) $5,15,45,135$
B) $5,14,13,12$
C) $12,36,108,216$
D) $5,17,47,137$

Question 12

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \frac { ( - 1 ) ^ { n + 1 } } { n + 2 }$$

A) $\frac { 1 } { 3 } , - \frac { 1 } { 4 } , \frac { 1 } { 5 } , - \frac { 1 } { 6 }$
B) $- \frac { 1 } { 3 } , \frac { 1 } { 4 } , - \frac { 1 } { 5 } , \frac { 1 } { 6 }$
C) $\frac { 1 } { 3 } , - \frac { 1 } { 8 } , \frac { 1 } { 15 } , - \frac { 1 } { 24 }$
D) $- \frac { 1 } { 4 } , \frac { 1 } { 5 } , - \frac { 1 } { 6 } , \frac { 1 } { 7 }$

Question 13

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \frac { n + 1 } { 2 n - 1 }$$

A) $2,1 , \frac { 4 } { 5 } , \frac { 5 } { 7 }$
B) $2 , - 1 , \frac { 4 } { 5 } , \frac { 5 } { 7 }$
C) $- 2,1 , \frac { 4 } { 5 } , \frac { 5 } { 7 }$
D) $- 2 , - 1 , \frac { 4 } { 5 } , \frac { 5 } { 7 }$

Question 14

Solve the problem.
A deposit of $11,000 is made in an account that earns 8% interest compounded quarterly. The balance in the account after n quarters is given by the sequence $$\mathrm { a } _ { \mathrm { n } } = 11,000 \left( 1 + \frac { 0.08 } { 4 } \right) ^ { \mathrm { n } } , \mathrm { n } = 1,2,3 , \ldots$$
Find the balance in the account after 4 years.

A) $\$ 15,100.64$
B) $\$ 5491.14$
C) $\$ 11,906.75$
D) $\$ 4257.14$

Question 15

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = ( - 3 ) ^ { n }$$

A) $- 3,9 , - 27,81$
B) $- 3 , - 9 , - 27 , - 81$
C) $3 , - 9 , - 27 , - 81$
D) $3 , - 9,27 , - 81$

Question 16

Use Recursion Formulas
$a _ { 1 } = - 5$ and $a _ { n } = a _ { n - 1 } - 3$ for $n \geq 2$

A) $- 5 , - 8 , - 11 , - 14$
B) $5,2 , - 1 , - 4$
C) $5,8,11,14$
D) $- 5 , - 4 , - 1,2$

Question 17

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = ( - 1 ) ^ { n } ( n + 6 )$$

A) $- 7,8 , - 9,10$
B) $- 7 , - 8 , - 9 , - 10$
C) $- 7 , - 16 , - 27 , - 40$
D) $7,8,9,10$

Question 18

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \left( \frac { 2 } { 5 } \right) ^ { n }$$

A) $\frac { 2 } { 5 } , \frac { 4 } { 25 } , \frac { 8 } { 125 } , \frac { 16 } { 625 }$
B) $1 , \frac { 2 } { 5 } , \frac { 4 } { 25 } , \frac { 8 } { 125 }$
C) $\frac { 2 } { 5 } , \frac { 2 } { 10 } , \frac { 2 } { 15 } , \frac { 2 } { 20 }$
D) $1 , \frac { 4 } { 25 } , \frac { 8 } { 125 } , \frac { 16 } { 625 }$

Question 19

Write the first four terms of the sequence whose general term is given.
$$a _ { n } = n - 4$$

A) $- 3 , - 2 , - 1,0$
B) $- 4 , - 3 , - 2 , - 1$
C) $- 1,0,1,2$
D) $- 16 , - 12 , - 8 , - 4$

Question 20

Solve the problem.
A deposit of $7000 is made in an account that earns 8% interest compounded quarterly. The balance in the account after n quarters is given by the sequence $\mathrm { a } _ { \mathrm { n } } = 7000 \left( 1 + \frac { 0.08 } { 4 } \right) ^ { \mathrm { n } } \quad \mathrm { n } = 1,2,3 , \ldots$
Find the balance in the account after 9 years.

A) $\$ 14,279.21$
B) $\$ 14,372.21$
C) $\$ 14,368.21$
D) $\$ 14,097.21$

Question 21

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \frac { ( n - 1 ) ! } { n ^ { 5 } }$$

A) $1 , \frac { 1 } { 32 } , \frac { 2 } { 243 } , \frac { 3 } { 512 }$
B) $\frac { 1 } { 5 } , \frac { 1 } { 10 } , \frac { 2 } { 15 } , \frac { 3 } { 10 }$
C) $0,0 , \frac { 2 } { 243 } , \frac { 3 } { 512 }$
D) $0,0 , \frac { 2 } { 15 } , \frac { 3 } { 10 }$

Question 22

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$$\frac { ( \mathrm { n } + 5 ) ! } { \mathrm { n } + 5 }$$

A) $( n + 4 )$ !
B) 1
C) 5 !
D) $n + 5$ !

Question 23

Use Summation Notation
$$\sum _ { i = 3 } ^ { 6 } ( 2 i - 3 )$$

A) 24
B) 21
C) 27
D) 15

Question 24

Use Summation Notation
$$\sum _ { i = 1 } ^ { 4 } 3 ^ { i }$$

A) 120
B) 84
C) 39
D) 30

Question 25

Use Summation Notation
$\sum _ { i = 4 } ^ { 7 } 9 i$

A) 198
B) 63
C) 99
D) 135

Question 26

Use Summation Notation
$$\sum _ { \mathrm { i } = 1 } ^ { 5 } ( \mathrm { i } - 10 )$$

A) $- 35$
В) $- 5$
C) $- 14$
D) $- 30$

Question 27

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \frac { n ^ { 5 } } { ( n - 1 ) ! }$$

A) $1,32 , \frac { 243 } { 2 } , \frac { 512 } { 3 }$
B) $5,10 , \frac { 15 } { 2 } , \frac { 10 } { 3 }$
C) $\frac { 1 } { 0 } , \frac { 32 } { 0 } , \frac { 243 } { 2 } , \frac { 512 } { 3 }$
D) $\frac { 5 } { 0 } , \frac { 10 } { 0 } , \frac { 15 } { 2 } , \frac { 10 } { 3 }$

Question 28

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$\frac { 9 ! } { 7 ! 2 ! }$

A) 36
B) 9
C) 0 !
D) 1

Question 29

Use Recursion Formulas
a1 = 3 and an = 4an-1 + 1 for n ≥ 2

A)3, 13, 53, 213
B)3, 13, 49, 193
C)3, 12, 48, 192
D)3, 11, 43, 171

Question 30

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$$\frac { n ( n + 2 ) ! } { ( n + 3 ) ! }$$

A) $\frac { \mathrm { n } } { \mathrm { n } + 3 }$
B) $\frac { \mathrm { n } } { 3 }$
C) $\frac { 1 } { n + 3 }$
D) $\frac { \mathrm { n } } { ( \mathrm { n } + 3 ) ! }$

Question 31

Use Summation Notation
$$\sum _ { i = 3 } ^ { 6 } \frac { 1 } { i + 9 }$$

A) $\frac { 543 } { 1820 }$
B) $- \frac { 51 } { 20 }$
C) $\frac { 40 } { 9 }$
D) 54

Question 32

Use Summation Notation
$$\sum _ { i = 3 } ^ { 5 } \left( i ^ { 2 } + 11 \right)$$

A) 83
B) 110
C) 57
D) 45

Question 33

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$\frac { 4 ! } { 6 ! }$

A) $\frac { 1 } { 30 }$
B) 30
C) 2 !
D) $\frac { 1 } { 2 ! }$

Question 34

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$\frac { 6 ! } { 4 ! }$

A) 30
B) $2 !$
C) $\frac { 6 } { 4 }$
D) 6

Question 35

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$\frac { 4 ! } { 3 ! }$

A) 4
B) 1
C) $\frac { 4 } { 3 }$
D) $4 !$

Question 36

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \frac { 3 ^ { n } } { ( n + 3 ) ! }$$

A) $\frac { 1 } { 8 } , \frac { 3 } { 40 } , \frac { 3 } { 80 } , \frac { 9 } { 560 }$
B) $\frac { 3 } { 7 } , \frac { 9 } { 8 } , 3 , \frac { 81 } { 10 }$
C) $\frac { 4 } { 3 } , \frac { 9 } { 5 } , \frac { 9 } { 2 } , \frac { 7 } { 81 }$
D) $\frac { 1 } { 8 } , \frac { 3 } { 40 } , \frac { 3 } { 40 } , \frac { 9 } { 280 }$

Question 37

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$$a _ { n } = \frac { 5 ( n + 1 ) ! } { n ! }$$

A) $10,15,20,25$
B) $10 , \frac { 15 } { 2 } , \frac { 10 } { 3 } , \frac { 25 } { 24 }$
C) $6,7,8,9$
D) $10 , \frac { 15 } { 2 } , \frac { 20 } { 3 } , \frac { 25 } { 4 }$ Evaluate the factorial expression.

Question 38

Use Summation Notation
$$\sum _ { i = 1 } ^ { 4 } \frac { 1 } { 7 i }$$

A) $\frac { 25 } { 84 }$
B) $\frac { 1 } { 28 }$
C) $\frac { 5 } { 28 }$
D) $\frac { 11 } { 42 }$

Question 39

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$\frac { 8 ! } { 4 ! 4 ! }$

A) 70
B) 140
C) 1680
D) 35

Question 40

Use Factorial Notation
Write the first four terms of the sequence whose general term is given.
$$a _ { n } = - 3 ( n + 2 ) !$$

A) $- 18 , - 72 , - 360 , - 2160$
B) $- 18,144 , - 1080,8640$
C) $- 6 , - 36 , - 216 , - 1440$
D) $- 6,18 , - 72,360$

Question 41

Use Summation Notation
$$\sum _ { i = 1 } ^ { 5 } \frac { ( i + 1 ) ! } { ( i + 2 ) ! }$$

A) $\frac { 153 } { 140 }$
B) $\frac { 547 } { 140 }$
C) $\frac { 39 } { 20 }$
D) $\frac { 81 } { 20 }$ Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation.

Question 42

Solve the problem.
The bar graph below shows a company's yearly profits from 1991 to 1999. Let an represent the company's profit, in millions, in year n, where n=1 corresponds to 1991, n = 2 corresponds to 1992, and so on.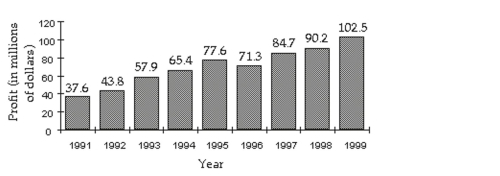
Find $\sum _ { i = 1 } ^ { 9 } a _ { i }$

A) $\$ 631$ million
B) $\$ 593.4$ million
C) $\$ 140.1$ million
D) $\$ 650.8$ million

Question 43

Use Summation Notation
$$\sum _ { i = 1 } ^ { 5 } \frac { ( - 1 ) ^ { \mathrm { i } + 1 } } { ( \mathrm { i } - 1 ) ! }$$

A) $\frac { 3 } { 8 }$
B) $- \frac { 3 } { 8 }$
C) $\frac { 5 } { 12 }$
D) $- \frac { 5 } { 12 }$

Question 44

Use Summation Notation
$a + a r + a r ^ { 2 } + \ldots + a r ^ { 11 }$

A) $\sum _ { \mathrm { i } = 1 } ^ { 12 } a \mathrm { r } ^ { \mathrm { i } - 1 }$
B) $\sum _ { \mathrm { i } = 1 } ^ { 11 } a r ^ { \mathrm { i } }$
C) $\sum _ { \mathrm { i } = 1 } ^ { 11 } ( \mathrm { ar } ) ^ { \mathrm { i } }$
D) $\sum _ { \mathrm { i } = 1 } ^ { 11 } ( \mathrm { ar } ) ^ { \mathrm { i - 1}}$ Express the sum using summation notation. Use a lower limit of summation not necessarily 1 and k for the index of summation.

Question 45

Use Summation Notation
$$\frac { 4 } { 5 } + \frac { 5 } { 6 } + \frac { 6 } { 7 } + \frac { 7 } { 8 } + \ldots + \frac { 16 } { 17 }$$

A) $\sum _ { k = 4 } ^ { 16 } \frac { k } { k + 1 }$
B) $\sum _ { \mathrm { k } = 5 } ^ { 16 } \frac { \mathrm { k } + 1 } { \mathrm { k } }$
C) $\sum _ { k = 4 } ^ { 16 } \frac { k + 1 } { k }$
D) $\sum _ { k = 5 } ^ { 16 } \frac { \mathrm { k } } { \mathrm { k } + 1 }$

Question 46

Use Summation Notation
$$( a + 1 ) + ( a + b ) + \left( a + b ^ { 2 } \right) + \ldots + \left( a + b ^ { n } \right)$$

A) $\sum _ { \mathrm { k } = 0 } ^ { \mathrm { n } } \left( \mathrm { a } + \mathrm { b } ^ { \mathrm { k } } \right)$
B) $\sum _ { k = 1 } ^ { n } \left( a + b ^ { k } \right)$
C) $\sum _ { k = 0 } ^ { n - 1 } \left( a + b ^ { k } \right)$
D) $\sum _ { k = 0 } ^ { n } a b ^ { k }$

Question 47

Use Summation Notation
$$3 + \frac { 7 } { 2 } + 4 + \frac { 9 } { 2 } + \ldots + 10$$

A) $\sum _ { k = 6 } ^ { 20 } \frac { k } { 2 }$
B) $\sum _ { \mathrm { k } = 1 } ^ { 20 } \frac { \mathrm { k } } { 2 }$
C) $\sum _ { \mathrm { k } = 6 } ^ { 10 } \frac { \mathrm { k } } { 2 }$
D) $\sum _ { k = 2 } ^ { 20 } \frac { k } { 2 }$

Question 48

Use Summation Notation
$$3 ^ { 2 } + 6 ^ { 3 } + 9 ^ { 4 } + \ldots + 24 ^ { 9 }$$

A) $\sum _ { i = 1 } ^ { 8 } ( 3 i ) ^ { i + 1 }$
B) $\sum _ { \mathrm { i } = 1 } ^ { 8 } ( 3 \mathrm { i } ) ^ { \mathrm { i } }$
C) $\sum _ { \mathrm { i } = 1 } ^ { 8 } 2 ( \mathrm { i } - 1 ) ^ { \mathrm { i } + 1 }$
D) $\sum _ { i = 1 } ^ { 8 } 3 i ^ { 2 i - 1}$

Question 49

Use Summation Notation
$$5 + 6 + 7 + 8 + \ldots + 29$$

A) $\sum _ { k = 4 } ^ { 28 } ( k + 1 )$
B) $\sum _ { k = 5 } ^ { 29 } ( \mathrm { k } + 1 )$
C) $\sum _ { k = 6 } ^ { 30 } ( k + 1 )$
D) $\sum _ { k = 1 } ^ { 24 } ( \mathrm { k } + 1 )$

Question 50

Use Summation Notation
$$\sum _ { i = 4 } ^ { 7 } \frac { i ! } { ( i - 1 ) ! }$$

A) 22
B) 14
C) $\frac { 7 } { 3 }$
D) 7

Question 51

Use Summation Notation
$11 + 14 + 17 + 20 + \ldots + 35$

A) $\sum _ { \mathrm { k } = 2 } ^ { 10 } 3 \mathrm { k } + 5$
B) $\sum _ { k = 0 } ^ { 24 } 3 k + 5$
C) $\sum _ { k = 1 } ^ { 10 } 3 k + 5$
D) $\sum _ { k = 2 } ^ { 24 } 3 k + 5$

Question 52

Use Summation Notation
$$\sum _ { i = 5 } ^ { 9 } 4$$

A) 20
B) 140
C) 16
D) 120

Question 53

Use Summation Notation
$$\frac { 1 } { 3 } + \frac { 1 } { 2 } + \frac { 3 } { 5 } + \ldots + \frac { 7 } { 8 }$$

A) $\sum _ { i = 1 } ^ { 14 } \frac { i } { i + 2 }$
B) $\sum _ { i = 0 } ^ { 14 } \frac { i } { i + 2 }$
C) $\sum _ { i = 1 } ^ { n } \frac { i } { i + 2 }$
D) $\sum _ { i = 2 } ^ { 14 } \frac { \mathrm { i } } { \mathrm { i } + 1 }$

Question 54

Use Summation Notation
$$3 + 12 + 27 + \ldots + 108$$

A) $\sum _ { i = 1 } ^ { 6 } 3 i ^ { 2 }$
B) $\sum _ { i = 0 } ^ { 6 } 3 i ^ { 2 }$
C) $\sum _ { i = 1 } ^ { 6 } i ^ { 2 }$
D) $\sum _ { i = 1 } ^ { 6 } 3 ^ { 2 } i$

Question 55

Use Summation Notation
$$a + 1 + \frac { a + 2 } { 2 } + \ldots + \frac { a + 5 } { 5 }$$

A) $\sum _ { i = 1 } ^ { 5 } \frac { a + i } { i }$
B) $\sum _ { i = 0 } ^ { 5 } \frac { a + i } { i }$
C) $\sum _ { i = 0 } ^ { n } \frac { a + i } { i }$
D) $\sum _ { i = 1 } ^ { n } \frac { a + i } { i }$

Question 56

Use Summation Notation
$$\sum _ { i = 1 } ^ { 4 } \left( - \frac { 1 } { 3 } \right) ^ { i }$$

A) $- \frac { 20 } { 81 }$
B) $\frac { 20 } { 81 }$
C) $- \frac { 16 } { 81 }$
D) $\frac { 40 } { 81 }$

Question 57

Use Summation Notation
$$\sum _ { k = 1 } ^ { 4 } ( - 1 ) ^ { k } ( k + 15 )$$

A) 2
B) $- 70$
C) 70
D) 62

Question 58

Use Summation Notation
$a + a r + a r ^ { 2 } + \ldots + a r ^ { 14 }$

A) $\sum _ { \mathrm { k } = 0 } ^ { 14 } a \mathrm { r } ^ { \mathrm { k } }$
B) $\sum _ { \mathrm { k } = 1 } ^ { 15 } a \mathrm { r } ^ { \mathrm { k } }$
C) $\sum _ { \mathrm { k } = 0 } ^ { 14 } ( \mathrm { ar } ) ^ { \mathrm { k } }$
D) $\sum _ { k = 1 } ^ { 14 } a r ^ { k }$

Question 59

Use Summation Notation
3 + 6 + 9 + . . . + 21 A) $\sum _ { i = 1 } ^ { 7 } 3 i$
B) $\sum _ { i = 0 } ^ { 7 } 3 i$
C) $\sum _ { i = 1 } ^ { 7 } i ^ { 2 }$
D) $\sum _ { i = 1 } ^ { 7 } 3 i ^ { 2 }$

Question 60

Use Summation Notation
$$\sum _ { k = 2 } ^ { 4 } k ( k - 4 )$$

A) $- 7$
B) $- 10$
C) $- 4$
D) 6 )6

Question 61

Write Terms of an Arithmetic Sequence
$$a _ { n } = a _ { n } - 1 - 7 ; a _ { 1 } = 5$$

A) $5 , - 2 , - 9 , - 16 , - 23$
B) $4 , - 3 , - 10 , - 17 , - 24$
C) $- 7 , - 2,3,8,13$
D) $5 , - 7 , - 2 , - 9 , - 16$

Question 62

Find the Common Difference for an Arithmetic Sequence
-9, -14, -19, -24, . . .

A)-5B)-15
C)-10
D)15

Question 63

Find the Common Difference for an Arithmetic Sequence
794, 786, 778, 770, . . .

A)-8
B)8
C)794
D)-794

Question 64

Write Terms of an Arithmetic Sequence
$$a _ { n } = a _ { n } - 1 + 7.3 ; a _ { 1 } = - 7$$

A) $- 7,0.3,7.6,14.9,22.2$
В) $- 8 , - 0.7,6.6,13.9,21.2$
C) $7.3,0.3 , - 6.7 , - 13.7 , - 20.7$
D) $- 7,7.3,0.3,7.6,14.9$

Question 65

Use the Formula for the General Term of an Arithmetic Sequence
Find $a _ { 11 }$ when $a _ { 1 } = 21 , d = - 3$ .

A) $- 9$
B) $- 12$
C) $- 30$
D) 51

Question 66

Find the Common Difference for an Arithmetic Sequence
8, 13, 18, 23, . . .

A)5
B)15
C)-5D)-15

Question 67

Write Terms of an Arithmetic Sequence
$$\mathrm { a } _ { \mathrm { n } } = \mathrm { a } _ { \mathrm { n } } - 1 - 1.8 ; \mathrm { a } _ { 1 } = 6$$

A) $6,4.2,2.4,0.6 , - 1.2$
B) $5,3.2,1.4 , - 0.4 , - 2.2$
C) $- 1.8,4.2,10.2,16.2,22.2$
D) $6 , - 1.8,4.2,2.4,0.6$

Question 68

Write Terms of an Arithmetic Sequence
a1 = -30; d = 7

A)-30, -23, -16, -9, -2B)-16, -9, -2, 5, 12
C)-2, -9, -16, -23, -30
D)-16, -23, -30, -37, -44

Question 69

Write Terms of an Arithmetic Sequence
$$a _ { n } = a _ { n - 1} - \frac { 1 } { 3 } ; a _ { 1 } = - \frac { 1 } { 2 }$$

A) $- \frac { 1 } { 2 } , - \frac { 5 } { 6 } , - \frac { 7 } { 6 } , - \frac { 3 } { 2 } , - \frac { 11 } { 6 }$
B) $- \frac { 1 } { 2 } , - \frac { 1 } { 6 } , \frac { 1 } { 6 } , \frac { 1 } { 2 } , \frac { 5 } { 6 }$
C) $- \frac { 1 } { 2 } , - 1 , - \frac { 3 } { 2 } , - 2 , - \frac { 5 } { 2 }$
D) $- \frac { 1 } { 2 } , - \frac { 5 } { 6 } , - 1 , - \frac { 4 } { 3 } , - \frac { 5 } { 3 }$

Question 70

Write Terms of an Arithmetic Sequence
$a _ { 1 } = - \frac { 7 } { 3 } , d = - \frac { 5 } { 3 }$

A) $- \frac { 7 } { 3 } , - 4 , - \frac { 17 } { 3 } , - \frac { 22 } { 3 } , - 9$
B) $- \frac { 7 } { 3 } , - \frac { 2 } { 3 } , 1 , \frac { 8 } { 3 } , \frac { 13 } { 3 }$
C) $- \frac { 7 } { 3 } , - 2 , - \frac { 17 } { 9 } , - \frac { 11 } { 6 } , - \frac { 9 } { 5 }$
D) $- \frac { 7 } { 3 } , - \frac { 1 } { 3 } , \frac { 1 } { 3 } , \frac { 2 } { 3 } , \frac { 13 } { 15 }$

Question 71

Use the Formula for the General Term of an Arithmetic Sequence
Find $a 32$ when $a 1 = - 6 , d = 2$ .

A) 56
B) 58
C) $- 68$
D) $- 70$

Question 72

Use the Formula for the General Term of an Arithmetic Sequence
Find a8 when a $1 = - 9 , d = - 4$ .

A) $- 37$
В) $- 41$
C) 19
D) 23

Question 73

Find the Common Difference for an Arithmetic Sequence
6, 7, 8, 9, . . .

A)1
B)3
C)0.75
D)6

Question 74

Write Terms of an Arithmetic Sequence
$$a _ { n } = a _ { n } - 1 + 4 ; a _ { 1 } = - 18$$

A) $- 18 , - 14 , - 10 , - 6 , - 2$
B) $- 19 , - 15 , - 11 , - 7 , - 3$
C) $4 , - 14 , - 32 , - 50 , - 68$
D) $- 18,4 , - 14 , - 10 , - 6$

Question 75

Write Terms of an Arithmetic Sequence
a1 = 6; d = -1

A)6, 5, 4, 3, 2
B)0, 6, 5, 4, 3C)-6, -5, -4, -3, -2D)10, 8, 6, 4, 2

Question 76

Write Terms of an Arithmetic Sequence
a1 = 5; d = 3

A)5, 8, 11, 14, 17
B)8, 11, 14, 17, 20
C)0, 5, 8, 11, 14
D)5, 7, 9, 11, 13

Question 77

Write Terms of an Arithmetic Sequence
$$\mathrm { a } _ { 1 } = - \frac { 2 } { 3 } ; \mathrm { d } = - \frac { 1 } { 9 }$$

A) $- \frac { 2 } { 3 } , - \frac { 7 } { 9 } , - \frac { 8 } { 9 } , - 1 , - \frac { 10 } { 9 }$
B) $- \frac { 2 } { 3 } , - \frac { 5 } { 9 } , - \frac { 4 } { 9 } , - \frac { 1 } { 3 } , - \frac { 2 } { 9 }$
C) $- \frac { 2 } { 3 } , - \frac { 4 } { 3 } , - 2 , - \frac { 8 } { 3 } , - \frac { 10 } { 3 }$
D) $- \frac { 2 } { 3 } , - \frac { 7 } { 9 } , - \frac { 4 } { 9 } , - 1 , - \frac { 2 } { 9 }$

Question 78

Solve the problem.
The finite sequence whose general term is $$a _ { n } = 0.16 n ^ { 2 } - 1.06 n + 7.25$$
where $\mathrm { n } = 1,2,3 , \ldots , 9$ models the total operating costs, in millions of dollars, for a company from 1991 through $1999 .$
Find $\sum _ { i = 1 } ^ { 5 } a _ { i }$

A) $\$ 29.15$ million
B) $\$ 31.75$ million
C) $\$ 23.2$ million
D) $\$ 25.4$ million

Question 79

Write Terms of an Arithmetic Sequence
a1 = 13; d = -3

A)13, 10, 7, 4, 1B)16, 13, 10, 7, 4C)10, 7, 4, 1, -2D)13, 10, 6, 4, 1

Question 80

Use the Formula for the General Term of an Arithmetic Sequence
Find a 21 when a1 = 5, d = 1.

A)25
B)26
C)- 15
D)- 16