Deck 2: Parallel Lines
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/13
Play
Full screen (f)
Deck 2: Parallel Lines
1
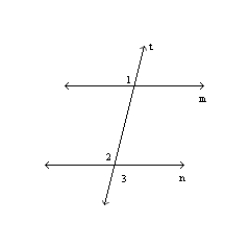
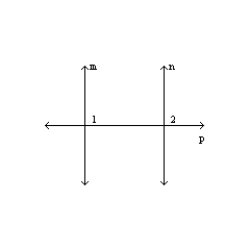
Supply missing reasons for this proof.
Given: m || n
Prove:
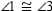 S1. m || n R1.
S1. m || n R1.S2.
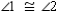 R2.
R2.S3.
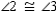 R3.
R3.S4.
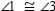 R4.
R4.R1. Given
R2. If 2 parallel line are cut by a transversal, then corresponding angles are congruent.
R3. If two lines intersect, the vertical angles formed are congruent.
R4. Transitive Property of Congruence
R2. If 2 parallel line are cut by a transversal, then corresponding angles are congruent.
R3. If two lines intersect, the vertical angles formed are congruent.
R4. Transitive Property of Congruence
2
Use an indirect proof to complete the following problem.
Given: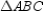 (not shown)
(not shown)
Prove: and
and 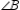 cannot both be right angles.
cannot both be right angles.
Given:
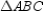 (not shown)
(not shown)Prove:
 and
and 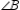 cannot both be right angles.
cannot both be right angles.Suppose that  and
and 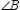 are both be right angles. Then
are both be right angles. Then 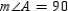 and
and 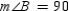 .
.
By the Protractor Postulate,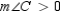 . Then
. Then 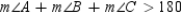 . But this last
. But this last
statement contradicts the fact that the sum of teh three interior angles of a triangle is exactly 180. Thus, the supposition must be false and it follows that and
and 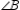 cannot both be right angles.
cannot both be right angles.
 and
and 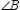 are both be right angles. Then
are both be right angles. Then 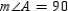 and
and 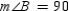 .
.By the Protractor Postulate,
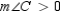 . Then
. Then 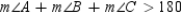 . But this last
. But this laststatement contradicts the fact that the sum of teh three interior angles of a triangle is exactly 180. Thus, the supposition must be false and it follows that
 and
and 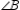 cannot both be right angles.
cannot both be right angles. 3
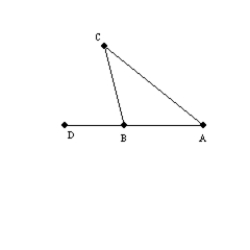
Supply missing reasons for the following proof.
Given:
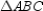 with D-B-A
with D-B-AProve:
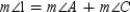 S1.
S1. 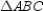 with D-B-A R1.
with D-B-A R1.S2.
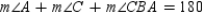 R2.
R2.S3.
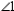 and
and 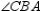 are supp. R3.
are supp. R3.S4.
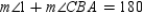 R4.
R4.S5.
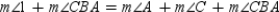 R5.
R5.S6.
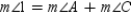 R6.
R6.R1. Given
R2. The sum of the interior angles of a triangle is 180.
R3. If the exterior sides of 2 adjacent agles form a line, these angles are supplementary.
R4. Definition of supplementary angles
R5. Substitution Property of Equality
R6. Subtraction Property of Equality
R2. The sum of the interior angles of a triangle is 180.
R3. If the exterior sides of 2 adjacent agles form a line, these angles are supplementary.
R4. Definition of supplementary angles
R5. Substitution Property of Equality
R6. Subtraction Property of Equality
4
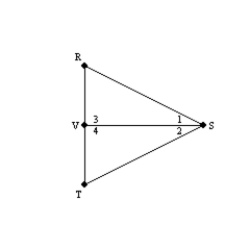
Supply missing statements and missing reasons for the following proof.
Given:
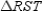 so that
so that 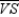 bisects
bisects 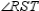 ;
;also,
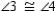 Prove:
Prove: 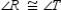 S1.
S1. 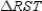 so that
so that 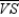 bisects
bisects 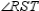 R1.
R1.S2. R2.
S3. R3. Given
S4. R4. If 2 angles of one triangle are congruent to
2 angles of a second triangle, then the third angles
of these triangles are also congruent.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
5
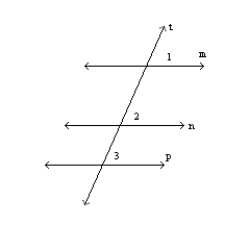
Supply missing statements in the following proof.
Given:
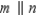 and
and 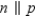 Prove:
Prove: 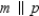 S1. R1. Given
S1. R1. GivenS2. R2. If 2 parallel lines are cut by a transversal, corr. angles are congruent.
S3. R3. Given
S4. R4. Same as #2.
S5. R5. Transitive Property of Congruence
S6. R6. If 2 lines are cut by a transversal so that corresponding angles
are congruent, then these lines are parallel.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
6
Explain the following statement.
The measure of each interior angle of an equiangular triangle is 60.
The measure of each interior angle of an equiangular triangle is 60.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
7
Supply missing statements and missing reasons for the following proof.
Given:
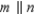 and transversal p;
and transversal p;  is a right angle
is a right angleProve:
 is a right angle
is a right angleS1.
 and transversal p R1.
and transversal p R1.S2.
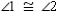 R2.
R2.S3. R3. Congruent measures have equal measures.
S4.
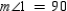 R4.
R4.S5. R5. Substitution Property of Equality
S6. R6. Definition of a right angle

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
8
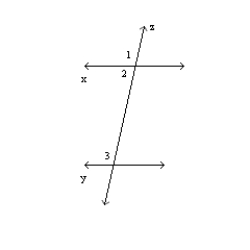
In the figure, x || y and transversal z. Explain why
 and
and  must be supplementary.
must be supplementary.
Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
9
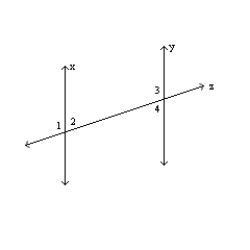
Supply missing statements and reasons for the foloowing proof.
Given:
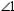 is supplementary to
is supplementary to 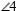 Prove:
Prove: 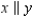 S1. R1.
S1. R1.S2.
 is supp. to
is supp. to 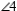 R2. If the ext. sides of 2 adj. angles form a line, the angles are supp.
R2. If the ext. sides of 2 adj. angles form a line, the angles are supp.S3. R3. Angles supp. to the same angle are congruent.
S4. R4.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
10
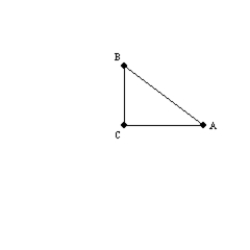
In the triangle shown,
 is a right angle.Explain why
is a right angle.Explain why  and
and 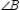 are complementary.
are complementary.
Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
11
Use an indirect proof to complete the following problem.
Given: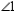 and
and  are supplementary (no drawing)
are supplementary (no drawing)
Prove: and
and  are not both obtuse angles.
are not both obtuse angles.
Given:
 and
and  are supplementary (no drawing)
are supplementary (no drawing)Prove:
 and
and  are not both obtuse angles.
are not both obtuse angles.
Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
12
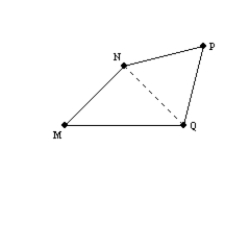
Using the drawing provided, explain the following statement.
The sum of the interior angles of a quadrilateral is 360.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
13
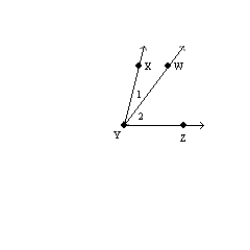
Use an indirect proof to complete the following problem.
Given:
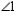 is not congruent to
is not congruent to  Prove:
Prove: 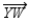 does not bisect
does not bisect 

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck


