Deck 18: Externalities and Public Goods
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/12
Play
Full screen (f)
Deck 18: Externalities and Public Goods
1
A firm in a perfectly competitive industry has patented a new process for making widgets. The new process lowers the firm's average cost, meaning that this firm alone (although still a price taker) can earn real economic profits in the long run.
a. If the market price is $20 per widget and the firm's marginal cost is given by MC= 0.4 q , where q is the daily widget production for the firm, how many widgets will the firm produce?
b. Suppose a government study has found that the firm's new process is polluting the air and estimates the social marginal cost of widget production by this firm to be SMC= 0.5 q. If the market price is still $20, what is the socially optimal level of production for the firm? What should be the rate of a government-imposed excise tax to bring about this optimal level of production?
c. Graph your results.
a. If the market price is $20 per widget and the firm's marginal cost is given by MC= 0.4 q , where q is the daily widget production for the firm, how many widgets will the firm produce?
b. Suppose a government study has found that the firm's new process is polluting the air and estimates the social marginal cost of widget production by this firm to be SMC= 0.5 q. If the market price is still $20, what is the socially optimal level of production for the firm? What should be the rate of a government-imposed excise tax to bring about this optimal level of production?
c. Graph your results.
a) A firm in a perfectly competitive market is a price taker. Hence, it maximizes it profits by producing at a point at which marginal cost is equal to the prevailing price.
As
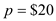 and
and
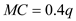 For maximizing profit, firm will equate the price and the marginal cost. We get,
For maximizing profit, firm will equate the price and the marginal cost. We get,
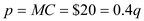 From this we get the optimal quantity
From this we get the optimal quantity
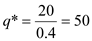 b) The social optimum is given at the point where social marginal cost is equal to the social marginal benefit. In the case of a perfectly competitive firm, the social marginal benefit would be equal to the price. The social marginal cost however would be greater than the private marginal cost of the firm. The social marginal cost is given by 0.5q.
b) The social optimum is given at the point where social marginal cost is equal to the social marginal benefit. In the case of a perfectly competitive firm, the social marginal benefit would be equal to the price. The social marginal cost however would be greater than the private marginal cost of the firm. The social marginal cost is given by 0.5q.
So for social optimum output, the following should hold
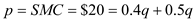 From this we get the socially optimal quantity
From this we get the socially optimal quantity
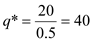 The government can put a tax on each unit produced to get the firm to produce the socially optimal quantity while maximizing its profit. Let such a tax be t. Then the following should hold.
The government can put a tax on each unit produced to get the firm to produce the socially optimal quantity while maximizing its profit. Let such a tax be t. Then the following should hold.
For maximizing profit, firm will equate the price and the marginal cost. We get,
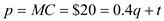 Since
Since
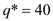 Then
Then
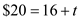 This gives us the excise tax that the government should charge
This gives us the excise tax that the government should charge
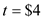 c) The above results can also be shown in the graph below
c) The above results can also be shown in the graph below
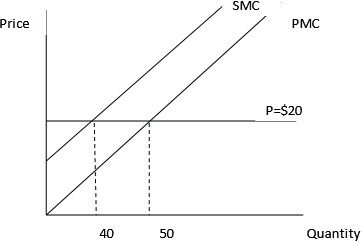
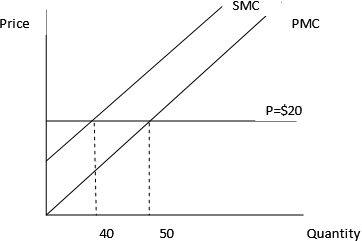
As
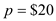 and
and 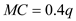 For maximizing profit, firm will equate the price and the marginal cost. We get,
For maximizing profit, firm will equate the price and the marginal cost. We get,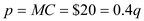 From this we get the optimal quantity
From this we get the optimal quantity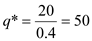 b) The social optimum is given at the point where social marginal cost is equal to the social marginal benefit. In the case of a perfectly competitive firm, the social marginal benefit would be equal to the price. The social marginal cost however would be greater than the private marginal cost of the firm. The social marginal cost is given by 0.5q.
b) The social optimum is given at the point where social marginal cost is equal to the social marginal benefit. In the case of a perfectly competitive firm, the social marginal benefit would be equal to the price. The social marginal cost however would be greater than the private marginal cost of the firm. The social marginal cost is given by 0.5q.So for social optimum output, the following should hold
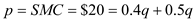 From this we get the socially optimal quantity
From this we get the socially optimal quantity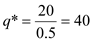 The government can put a tax on each unit produced to get the firm to produce the socially optimal quantity while maximizing its profit. Let such a tax be t. Then the following should hold.
The government can put a tax on each unit produced to get the firm to produce the socially optimal quantity while maximizing its profit. Let such a tax be t. Then the following should hold.For maximizing profit, firm will equate the price and the marginal cost. We get,
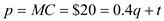 Since
Since 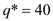 Then
Then 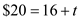 This gives us the excise tax that the government should charge
This gives us the excise tax that the government should charge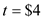 c) The above results can also be shown in the graph below
c) The above results can also be shown in the graph below

2
On the island of Pago Pago there are 2 lakes and 20 anglers. Each angler can fish on either lake and keep the average catch on his particular lake. On Lake x , the total number of fish caught is given by
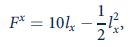
where l x is the number of people fishing on the lake. For Lake y, the relationship is
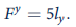
a. Under this organization of society, what will be the total number of fish caught?
b. The chief of Pago Pago, having once read an economics book, believes it is possible to increase the total number of fish caught by restricting the number of people allowed to fish on Lake x. What number should be allowed to fish on Lake x in order to maximize the total catch of fish? What is the number of fish caught in this situation?
c. Being opposed to coercion, the chief decides to require a fishing license for Lake x. If the licensing procedure is to bring about the optimal allocation of labor, what should the cost of a license be (in terms of fish)?
d. Explain how this example sheds light on the connection between property rights and externalities.
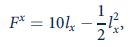
where l x is the number of people fishing on the lake. For Lake y, the relationship is
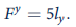
a. Under this organization of society, what will be the total number of fish caught?
b. The chief of Pago Pago, having once read an economics book, believes it is possible to increase the total number of fish caught by restricting the number of people allowed to fish on Lake x. What number should be allowed to fish on Lake x in order to maximize the total catch of fish? What is the number of fish caught in this situation?
c. Being opposed to coercion, the chief decides to require a fishing license for Lake x. If the licensing procedure is to bring about the optimal allocation of labor, what should the cost of a license be (in terms of fish)?
d. Explain how this example sheds light on the connection between property rights and externalities.
a) Since there are 2 lakes, each angler while deciding which lake to fish in compares the average catch of the lakes. For equilibrium, it must be true that the average catch of both the lakes be equal otherwise an angler will have the incentive to switch to the lake offering higher average catch. Let l x be the number of anglers working on lake x.
Hence, at equilibrium

 So,
So,
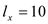 As
As
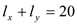 ...... (1)
...... (1)
So,
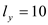 Total number of fish caught is given by
Total number of fish caught is given by
 ...... (2)
...... (2)
Substituting the values we get,
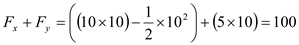 b) The total number of fish caught is given by equation (2) reproduced below
b) The total number of fish caught is given by equation (2) reproduced below
 We maximize the profit function below.
We maximize the profit function below.
The constraint is given by
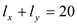 His budget constraint is:
His budget constraint is:
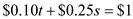 Setting the Lagrange
Setting the Lagrange
 Yields the first order conditions
Yields the first order conditions
 ....... (3)
....... (3)
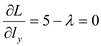 ...... (4)
...... (4)
Dividing equation (3) by equation (4), we get
 So,
So,
 Substitution of this value of
Substitution of this value of
 into the constraint
into the constraint
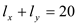 We get
We get
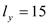 The number of fish caught is then given by
The number of fish caught is then given by
 c) Instead of restricting the number of people allowed to fish in lake x, a license can also be sold at price t for fishing in that lake. The price of t should be such that at the
c) Instead of restricting the number of people allowed to fish in lake x, a license can also be sold at price t for fishing in that lake. The price of t should be such that at the
social optimum allocation of
 the following condition holds.
the following condition holds.
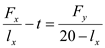 So,
So,
 d) On comparing part a) and part b) we see that the total catch of fish increases when property rights are assigned. This is because when an angler decides which lake to fish in, he considers the average catch and not the marginal catch. Though the average catch maybe positive, the marginal catch maybe negative because of externality. The angler's decision to fish in lake x decreases the catch of the anglers already fishing. He does non take that into account in his decision. However, when property rights are assigned this externality is taken into account.
d) On comparing part a) and part b) we see that the total catch of fish increases when property rights are assigned. This is because when an angler decides which lake to fish in, he considers the average catch and not the marginal catch. Though the average catch maybe positive, the marginal catch maybe negative because of externality. The angler's decision to fish in lake x decreases the catch of the anglers already fishing. He does non take that into account in his decision. However, when property rights are assigned this externality is taken into account.
Hence, at equilibrium

 So,
So,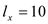 As
As 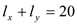 ...... (1)
...... (1)So,
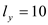 Total number of fish caught is given by
Total number of fish caught is given by ...... (2)
...... (2)Substituting the values we get,
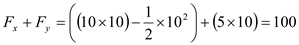 b) The total number of fish caught is given by equation (2) reproduced below
b) The total number of fish caught is given by equation (2) reproduced below We maximize the profit function below.
We maximize the profit function below.The constraint is given by
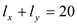 His budget constraint is:
His budget constraint is: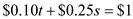 Setting the Lagrange
Setting the Lagrange Yields the first order conditions
Yields the first order conditions ....... (3)
....... (3)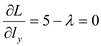 ...... (4)
...... (4)Dividing equation (3) by equation (4), we get
 So,
So, Substitution of this value of
Substitution of this value of  into the constraint
into the constraint 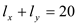 We get
We get 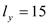 The number of fish caught is then given by
The number of fish caught is then given by c) Instead of restricting the number of people allowed to fish in lake x, a license can also be sold at price t for fishing in that lake. The price of t should be such that at the
c) Instead of restricting the number of people allowed to fish in lake x, a license can also be sold at price t for fishing in that lake. The price of t should be such that at the social optimum allocation of
 the following condition holds.
the following condition holds.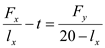 So,
So,  d) On comparing part a) and part b) we see that the total catch of fish increases when property rights are assigned. This is because when an angler decides which lake to fish in, he considers the average catch and not the marginal catch. Though the average catch maybe positive, the marginal catch maybe negative because of externality. The angler's decision to fish in lake x decreases the catch of the anglers already fishing. He does non take that into account in his decision. However, when property rights are assigned this externality is taken into account.
d) On comparing part a) and part b) we see that the total catch of fish increases when property rights are assigned. This is because when an angler decides which lake to fish in, he considers the average catch and not the marginal catch. Though the average catch maybe positive, the marginal catch maybe negative because of externality. The angler's decision to fish in lake x decreases the catch of the anglers already fishing. He does non take that into account in his decision. However, when property rights are assigned this externality is taken into account. 3
Suppose the oil industry in Utopia is perfectly competitive and that all firms draw oil from a single (and practically inexhaustible) pool. Assume that each competitor believes that it can sell all the oil it can produce at a stable world price of $10 per barrel and that the cost of operating a well for one year is $1,000.
Total output per year (Q) of the oil field is a function of the number of wells (n) operating in the field. In particular,
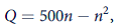
and the amount of oil produced by each well (q) is given by

a. Describe the equilibrium output and the equilibrium number of wells in this perfectly competitive case. Is there a divergence between private and social marginal cost in the industry?
b. Suppose now that the government nationalizes the oil field. How many oil wells should it operate? What will total output be? What will the output per well be?
c. As an alternative to nationalization, the Utopian government is considering an annual license fee per well to discourage overdrilling. How large should this license fee be if it is to prompt the industry to drill the optimal number of wells?
Total output per year (Q) of the oil field is a function of the number of wells (n) operating in the field. In particular,
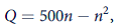
and the amount of oil produced by each well (q) is given by

a. Describe the equilibrium output and the equilibrium number of wells in this perfectly competitive case. Is there a divergence between private and social marginal cost in the industry?
b. Suppose now that the government nationalizes the oil field. How many oil wells should it operate? What will total output be? What will the output per well be?
c. As an alternative to nationalization, the Utopian government is considering an annual license fee per well to discourage overdrilling. How large should this license fee be if it is to prompt the industry to drill the optimal number of wells?
a) A perfectly competitive firm is a price taker. So to maximize profits the firm will equate the price with the marginal cost. The price is given as $10 per barrel. However, the cost is given in terms of$1000 per well. Hence, the cost per unit would be $1000/ q where q is the output per well. The firm would equate the MC with the price.
So,
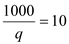 As,
As,
 ,
,
We get,
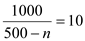 So the number of wells would be equal to 400.
So the number of wells would be equal to 400.
The optimum quantity is given by
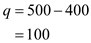 There is a divergence in the private marginal cost and social marginal cost in this industry because the number of wells a firm decides to put does not only affect his quantity but reduces the quantity that can be drilled by other firms. This is because quantity of each well is negatively related to the number of well. This fact is not taken into account by the firms.
There is a divergence in the private marginal cost and social marginal cost in this industry because the number of wells a firm decides to put does not only affect his quantity but reduces the quantity that can be drilled by other firms. This is because quantity of each well is negatively related to the number of well. This fact is not taken into account by the firms.
b) If the oil fields are nationalized then the government will maximize total profit and not the profit of individual firms.
Profit is given by
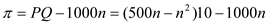 The first order condition yields
The first order condition yields
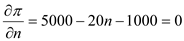 So optimal number of wells is 200
So optimal number of wells is 200
Total Output is given by
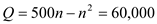 Output per well is given by
Output per well is given by
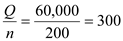 c) As shown in part b) the socially optimum number of wells is equal to 200. This can be achieved through the market mechanism if appropriate property rights are put in place. This can be done through putting an annual license fee in place.
c) As shown in part b) the socially optimum number of wells is equal to 200. This can be achieved through the market mechanism if appropriate property rights are put in place. This can be done through putting an annual license fee in place.
Let the license be l, then the following condition should hold for n = 200
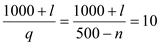 The above condition shows that the cost for operating a well annually goes up from $1000 to $1000+ l
The above condition shows that the cost for operating a well annually goes up from $1000 to $1000+ l
So for optimal number of wells equal to 200,
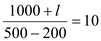 We get,
We get,
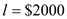
So,
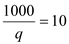 As,
As,  ,
, We get,
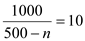 So the number of wells would be equal to 400.
So the number of wells would be equal to 400. The optimum quantity is given by
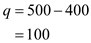 There is a divergence in the private marginal cost and social marginal cost in this industry because the number of wells a firm decides to put does not only affect his quantity but reduces the quantity that can be drilled by other firms. This is because quantity of each well is negatively related to the number of well. This fact is not taken into account by the firms.
There is a divergence in the private marginal cost and social marginal cost in this industry because the number of wells a firm decides to put does not only affect his quantity but reduces the quantity that can be drilled by other firms. This is because quantity of each well is negatively related to the number of well. This fact is not taken into account by the firms.b) If the oil fields are nationalized then the government will maximize total profit and not the profit of individual firms.
Profit is given by
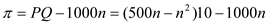 The first order condition yields
The first order condition yields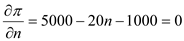 So optimal number of wells is 200
So optimal number of wells is 200 Total Output is given by
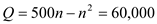 Output per well is given by
Output per well is given by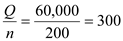 c) As shown in part b) the socially optimum number of wells is equal to 200. This can be achieved through the market mechanism if appropriate property rights are put in place. This can be done through putting an annual license fee in place.
c) As shown in part b) the socially optimum number of wells is equal to 200. This can be achieved through the market mechanism if appropriate property rights are put in place. This can be done through putting an annual license fee in place. Let the license be l, then the following condition should hold for n = 200
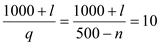 The above condition shows that the cost for operating a well annually goes up from $1000 to $1000+ l
The above condition shows that the cost for operating a well annually goes up from $1000 to $1000+ l So for optimal number of wells equal to 200,
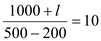 We get,
We get,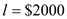
4
There is considerable legal controversy about product safety. Two extreme positions might be termed caveat emptor (let the buyer beware) and caveat vendor (let the seller beware). Under the former scheme producers would have no responsibility for the safety of their products: Buyers would absorb all losses. Under the latter scheme this liability assignment would be reversed: Firms would be completely responsible under law for losses incurred from unsafe products. Using simple supply and demand analysis, discuss how the assignment of such liability might affect the allocation of resources. Would safer products be produced if firms were strictly liable under law? How do possible information asymmetries affect your results?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose a monopoly produces a harmful externality. Use the concept of consumer surplus in a partial equilibrium diagram to analyze whether an optimal tax on the polluter would necessarily be a welfare improvement.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose there are only two individuals in society. Person A's demand curve for mosquito control is given by
q n = 100 - p ;
for person B, the demand curve for mosquito control is given by
q b = 200 - p :
a. Suppose mosquito control is a pure public good; that is, once it is produced, everyone benefits from it. What would be the optimal level of this activity if it could be produced at a constant marginal cost of $120 per unit?
b. If mosquito control were left to the private market, how much might be produced? Does your answer depend on what each person assumes the other will do?
c. If the government were to produce the optimal amount of mosquito control, how much will this cost? How should the tax bill for this amount be allocated between the individuals if they are to share it in proportion to benefits received from mosquito control?
q n = 100 - p ;
for person B, the demand curve for mosquito control is given by
q b = 200 - p :
a. Suppose mosquito control is a pure public good; that is, once it is produced, everyone benefits from it. What would be the optimal level of this activity if it could be produced at a constant marginal cost of $120 per unit?
b. If mosquito control were left to the private market, how much might be produced? Does your answer depend on what each person assumes the other will do?
c. If the government were to produce the optimal amount of mosquito control, how much will this cost? How should the tax bill for this amount be allocated between the individuals if they are to share it in proportion to benefits received from mosquito control?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose the production possibility frontier for an economy that produces one public good ( y ) and one private good ( x ) is given by
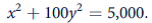
This economy is populated by 100 identical individuals, each with a utility function of the form
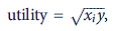
where x i is the individual's share of private good production (= x /100). Notice that the public good is nonexclusive and that everyone benefits equally from its level of production.
a. If the market for x and y were perfectly competitive, what levels of those goods would be produced? What would the typical individual's utility be in this situation?
b. What are the optimal production levels for x and y ? What would the typical individual's utility level be? How should consumption of good x be taxed to achieve this result? Hint: The numbers in this problem do not come out evenly, and some approximations should suffice.
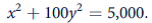
This economy is populated by 100 identical individuals, each with a utility function of the form
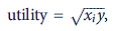
where x i is the individual's share of private good production (= x /100). Notice that the public good is nonexclusive and that everyone benefits equally from its level of production.
a. If the market for x and y were perfectly competitive, what levels of those goods would be produced? What would the typical individual's utility be in this situation?
b. What are the optimal production levels for x and y ? What would the typical individual's utility level be? How should consumption of good x be taxed to achieve this result? Hint: The numbers in this problem do not come out evenly, and some approximations should suffice.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
8
More on Lindahl equilibrium
The analysis of public goods in this chapter exclusively used a model with only two individuals. The results are readily generalized to n persons-a generalization pursued in this problem.
a. With n persons in an economy, what is the condition for efficient production of a public good? Explain how the characteristics of the public good are reflected in these conditions.
b. What is the Nash equilibrium in the provision of this public good to n persons? Explain why this equilibrium is inefficient. Also explain why the underprovision of this public good is more severe than in the two-person cases studied in the chapter.
c. How is the Lindahl solution generalized to n persons? Is the existence of a Lindahl equilibrium guaranteed in this more complex model?
The analysis of public goods in this chapter exclusively used a model with only two individuals. The results are readily generalized to n persons-a generalization pursued in this problem.
a. With n persons in an economy, what is the condition for efficient production of a public good? Explain how the characteristics of the public good are reflected in these conditions.
b. What is the Nash equilibrium in the provision of this public good to n persons? Explain why this equilibrium is inefficient. Also explain why the underprovision of this public good is more severe than in the two-person cases studied in the chapter.
c. How is the Lindahl solution generalized to n persons? Is the existence of a Lindahl equilibrium guaranteed in this more complex model?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
9
Taxing pollution
Suppose that there are n firms each producing the same good but with differing production functions. Output for each of these firms depends only on labor input, so the functions take the form q i = f i ( l i ). In its production activities each firm also produces some pollution, the amount of which is determined by a firm-specific function of labor input of the form g i ( l i ).
a. Suppose that the government wishes to place a cap of amount K on total pollution. What is the efficient allocation of labor among firms?
b. Will a uniform Pigovian tax on the output of each firm achieve the efficient allocation described in part (a)?
c. Suppose that, instead of taxing output, the Pigovian tax is applied to each unit of pollution. How should this tax be set? Will the tax yield the efficient allocation described in part (a)?
d. What are the implications of the problem for adopting pollution control strategies? (For more on this topic see the Extensions to this chapter.)
Suppose that there are n firms each producing the same good but with differing production functions. Output for each of these firms depends only on labor input, so the functions take the form q i = f i ( l i ). In its production activities each firm also produces some pollution, the amount of which is determined by a firm-specific function of labor input of the form g i ( l i ).
a. Suppose that the government wishes to place a cap of amount K on total pollution. What is the efficient allocation of labor among firms?
b. Will a uniform Pigovian tax on the output of each firm achieve the efficient allocation described in part (a)?
c. Suppose that, instead of taxing output, the Pigovian tax is applied to each unit of pollution. How should this tax be set? Will the tax yield the efficient allocation described in part (a)?
d. What are the implications of the problem for adopting pollution control strategies? (For more on this topic see the Extensions to this chapter.)

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
10
Vote trading
Suppose there are three individuals in society trying to rank three social states (A, B, and C). For each of the methods of social choice indicated, develop an example to show how the resulting social ranking of A, B, and C will be intransitive (as in the paradox of voting) or indeterminate.
a. Majority rule without vote trading.
b. Majority rule with vote trading.
c. Point voting where each voter can give 1, 2, or 3 points to each alternative and the alternative with the highest point total is selected.
Suppose there are three individuals in society trying to rank three social states (A, B, and C). For each of the methods of social choice indicated, develop an example to show how the resulting social ranking of A, B, and C will be intransitive (as in the paradox of voting) or indeterminate.
a. Majority rule without vote trading.
b. Majority rule with vote trading.
c. Point voting where each voter can give 1, 2, or 3 points to each alternative and the alternative with the highest point total is selected.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
11
Public choice of unemployment benefits
Suppose individuals face a probability of u that they will be unemployed next year. If they are unemployed they will receive unemployment benefits of b , whereas if they are employed they receive w (1 - t ), where t is the tax used to finance unemployment benefits. Unemployment benefits are constrained by the government budget constraint ub = tw (1 - u ).
a. Suppose the individual's utility function is given by
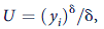
where 1 - ? is the degree of constant relative risk aversion. What would be the utility-maximizing choices for b and t?
b. How would the utility-maximizing choices for b and t respond to changes in the probability of unemployment, u ?
c. How would b and t change in response to changes in the risk aversion parameter ??
Suppose individuals face a probability of u that they will be unemployed next year. If they are unemployed they will receive unemployment benefits of b , whereas if they are employed they receive w (1 - t ), where t is the tax used to finance unemployment benefits. Unemployment benefits are constrained by the government budget constraint ub = tw (1 - u ).
a. Suppose the individual's utility function is given by
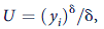
where 1 - ? is the degree of constant relative risk aversion. What would be the utility-maximizing choices for b and t?
b. How would the utility-maximizing choices for b and t respond to changes in the probability of unemployment, u ?
c. How would b and t change in response to changes in the risk aversion parameter ??

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
12
Probabilistic voting
Probabilistic voting is a way of modeling the voting process that introduces continuity into individuals' voting decisions. In this way, calculus-type derivations become possible. To take an especially simple form of this approach, suppose there are n voters and two candidates (labeled A and B) for elective office. Each candidate proposes a platform that promises a net gain or loss to each voter. These platforms are denoted by
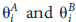 , where i = 1,... , n. The probability that a given voter will vote for candidate A is given by
, where i = 1,... , n. The probability that a given voter will vote for candidate A is given by
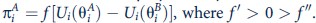 . The probability that the voter will vote for candidate B is
. The probability that the voter will vote for candidate B is
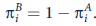
a. How should each candidate chose his or her platform so as to maximize the probability of winning the election subject to the constraint
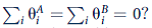 (Do these constraints seem to apply to actual political candidates?)
(Do these constraints seem to apply to actual political candidates?)
b. Will there exist a Nash equilibrium in platform strategies for the two candidates?
c. Will the platform adopted by the candidates be socially optimal in the sense of maximizing a utilitarian social welfare? [Social welfare is given by
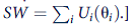
Probabilistic voting is a way of modeling the voting process that introduces continuity into individuals' voting decisions. In this way, calculus-type derivations become possible. To take an especially simple form of this approach, suppose there are n voters and two candidates (labeled A and B) for elective office. Each candidate proposes a platform that promises a net gain or loss to each voter. These platforms are denoted by
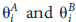 , where i = 1,... , n. The probability that a given voter will vote for candidate A is given by
, where i = 1,... , n. The probability that a given voter will vote for candidate A is given by 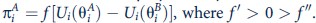 . The probability that the voter will vote for candidate B is
. The probability that the voter will vote for candidate B is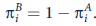
a. How should each candidate chose his or her platform so as to maximize the probability of winning the election subject to the constraint
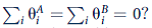 (Do these constraints seem to apply to actual political candidates?)
(Do these constraints seem to apply to actual political candidates?)b. Will there exist a Nash equilibrium in platform strategies for the two candidates?
c. Will the platform adopted by the candidates be socially optimal in the sense of maximizing a utilitarian social welfare? [Social welfare is given by
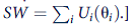

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck


