Deck 7: Linear Systems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/50
Play
Full screen (f)
Deck 7: Linear Systems
1
Let .
Perform the operation: .
a.
b.
c.
d.
e. none of these
Perform the operation: .
a.
b.
c.
d.
e. none of these
B
2
Which fraction appears in the partial fraction decomposition of ?
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.
A
3
Illustration shows three circles traced out by a figure skater during her performance.If the centers of the circles are the given distances apart, find the radius of each circle. 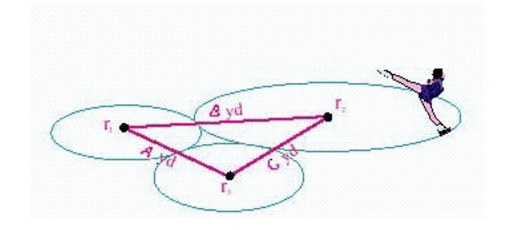
a.
b.
c.
d.
e.

a.
b.
c.
d.
e.
A
4
Solve the system by the addition method, if possible. If a solution exists, give the value of y.
a.
b. 1
d. 7
e. no solution
a.
b. 1
d. 7
e. no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
5
Find .
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
6
What is element of the inverse of the following matrix?
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
7
Find the inverse of the matrix.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
8
Find the inverse of the matrix.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
9
Find the graph of the linear inequality.
a.
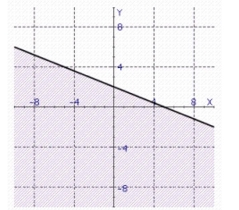
b.
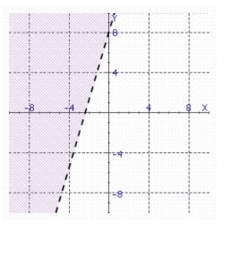
c.
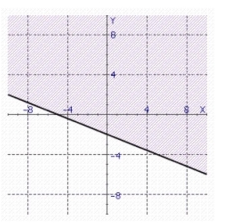
d.
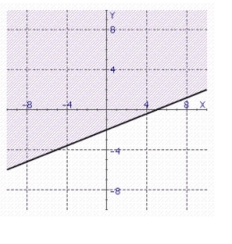
a.

b.

c.

d.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the determinant.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the system by the addition method, if possible. If a solution exists, give the value of x.
c. 4
d.
e. no solution
c. 4
d.
e. no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the system by Gauss-Jordan elimination, if possible. If is the solution to the system, give the value of .
a.
b. 5
c. 6
d.
e. no solution
a.
b. 5
c. 6
d.
e. no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
13
Use Cramer's rule to find the solution of the system, if possible.
a.
b.
c.
d. The system is inconsistent.
e. The equations are dependent.
a.
b.
c.
d. The system is inconsistent.
e. The equations are dependent.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
14
Find the graph of the linear inequality.
a.
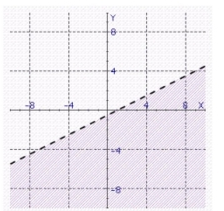
b.
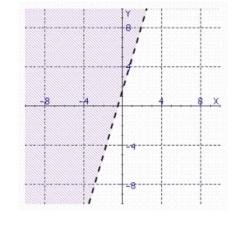
c.
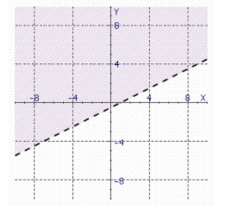
.
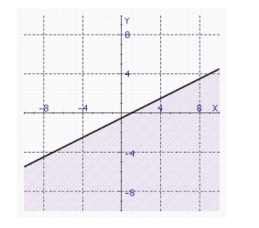
a.

b.

c.

.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the system using Gaussian elimination. If is the solution to the system, give the value of .
a.
b.
c. 21
d. 24
e.
a.
b.
c. 21
d. 24
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
16
Decompose the fraction into partial fractions.
a.
b.
c.
d.
e. none of these
a.
b.
c.
d.
e. none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
17
Decompose the fraction into partial fractions.
a.
b.
c.
d.
e. none of these
a.
b.
c.
d.
e. none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
18
Use a graphing calculator to approximate the solutions of the system.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
19
Find values of x and y, if any, that will make the matrices equal.
a.
b.
c.
d.
e. no solution
a.
b.
c.
d.
e. no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
20
Find the inverse of the matrix.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
21
Use Cramer's rule to find the solution of the system, if possible.
a.
b.
c.
d. The system is inconsistent.
e. The equations are dependent.
a.
b.
c.
d. The system is inconsistent.
e. The equations are dependent.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
22
Let .
Perform the operation: .
a.
b.
c.
d.
e. none of these
Perform the operation: .
a.
b.
c.
d.
e. none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
23
Use a graphing calculator to approximate the solutions of the system.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
24
Two artists make winter yard ornaments. They get for each wooden snowman they make and for each wooden Santa Claus. On average, Nina must work 4 hours and Roberta 3 hours to make a snowman. Nina must work 2 hours and Roberta 4 hours to make a Santa Claus. If neither wishes to work more than 20 hours per week, how many of each ornament should they make each week to maximize their income? The information is summarized in the table below.
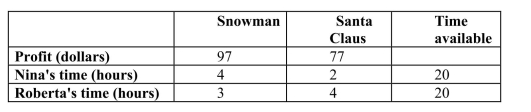
a. snowmen and 3 ornaments of Santa Claus:
b. snowmen and 4 ornaments of Santa Claus:
c. snowmen and 5 ornaments of Santa Claus:
d. snowmen and no ornaments of Santa Claus: \$485
e. 4 snowmen and 2 ornaments of Santa Claus:

a. snowmen and 3 ornaments of Santa Claus:
b. snowmen and 4 ornaments of Santa Claus:
c. snowmen and 5 ornaments of Santa Claus:
d. snowmen and no ornaments of Santa Claus: \$485
e. 4 snowmen and 2 ornaments of Santa Claus:

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
25
Minimize subject to the given constraints.
a. at
b. at
c. at
d. at
e. none of these
a. at
b. at
c. at
d. at
e. none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
26
Find the inverse of the matrix.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the system by Gauss-Jordan elimination, if possible. If (x, y) is the solution to the system, give the value of x.
a. 11
b.
c.
d. 10
e. no solution
a. 11
b.
c.
d. 10
e. no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
28
Find the inverse of the matrix.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
29
Find the solution set of the system.
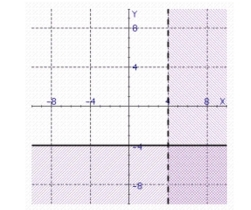
b.
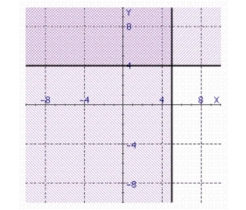
c.
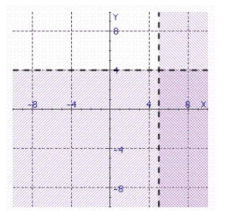
d.
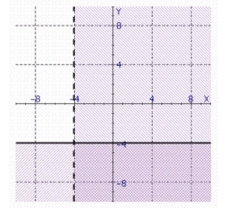

b.

c.

d.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
30
Find .
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
31
What is element of the inverse of the following matrix?
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
32
Illustration shows three circles traced out by a figure skater during her performance.If the centers of the circles are the given distances apart, find the radius of each circle. 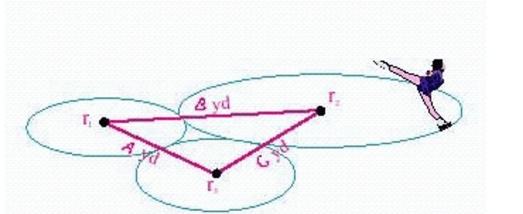
a.
b.
c.
d.
e.

a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
33
Find the inverse of the matrix.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the system by the addition method, if possible. If a solution exists, give the value of y.
a. 10
b. 6
c.
d. 4
e. no solution
a. 10
b. 6
c.
d. 4
e. no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the system using Gaussian elimination. If is the solution to the system, give the value of .
a.
b. 13
c.
d.
e.
a.
b. 13
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the determinant.
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the system by the addition method, if possible. If a solution exists, give the value of x.
a.
b.
c.
d.
e. no solution
a.
b.
c.
d.
e. no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
38
Find the solution set of the system.
a.
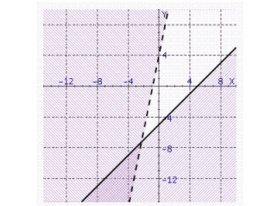
b.
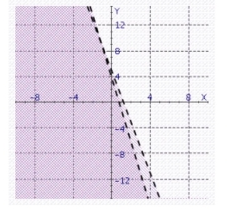
c.
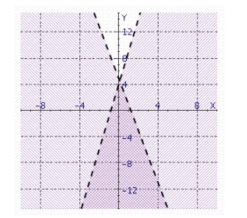
d.
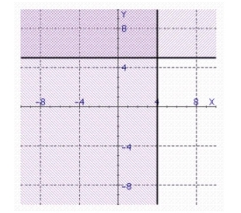
a.

b.

c.

d.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
39
Find values of x and y, if any, that will make the matrices equal.
a.
b.
c.
d.
e. no solution
a.
b.
c.
d.
e. no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
40
A diet requires at least 24 units of vitamin C and at least 26 units of vitamin B complex.Two food supplements are available that provide these nutrients, in the amounts and costs shown in the table
Below.How much of each should be used to minimize the cost?
a. grams of and 9 grams of cents
b. 1 gram of and 5 grams of B: 27 cents
c. grams of and 7 grams of B: 39 cents
d. grams of and 5 grams of B: 45 cents
e. 5 grams of and 2 grams of B: 20 cents
Below.How much of each should be used to minimize the cost?

a. grams of and 9 grams of cents
b. 1 gram of and 5 grams of B: 27 cents
c. grams of and 7 grams of B: 39 cents
d. grams of and 5 grams of B: 45 cents
e. 5 grams of and 2 grams of B: 20 cents

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
41
Two artists make winter yard ornaments.They get $83 for each wooden snowman they make and $74 for each wooden Santa Claus.On average, Nina must work 8 hours and Roberta 6 hours to make a
Snowman.Nina must work 4 hours and Roberta 8 hours to make a Santa Claus.If neither wishes to
Work more than 40 hours per week, how many of each ornament should they make each week to
Maximize their income? The information is summarized in the table below.
a. 4 snowmen and 3 ornaments of Santa Claus:
b. snowmen and 4 ornaments of Santa Claus:
c. 4 snowmen and 2 ornaments of Santa Claus:
d. snowmen and 5 ornaments of Santa Claus:
e. snowmen and no ornaments of Santa Claus:
Snowman.Nina must work 4 hours and Roberta 8 hours to make a Santa Claus.If neither wishes to
Work more than 40 hours per week, how many of each ornament should they make each week to
Maximize their income? The information is summarized in the table below.

a. 4 snowmen and 3 ornaments of Santa Claus:
b. snowmen and 4 ornaments of Santa Claus:
c. 4 snowmen and 2 ornaments of Santa Claus:
d. snowmen and 5 ornaments of Santa Claus:
e. snowmen and no ornaments of Santa Claus:

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
42
Find the solution set of the system.
a.
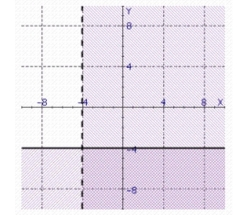
b.
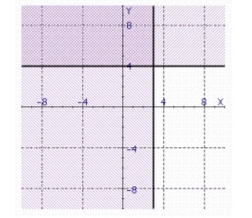
C.
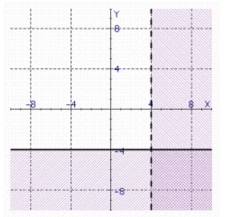
d.
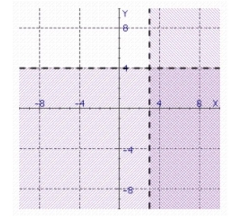
a.

b.

C.

d.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
43
Find the graph of the linear inequality.
a.
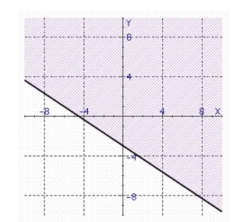
b.
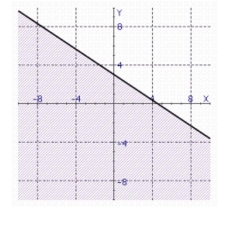
C.
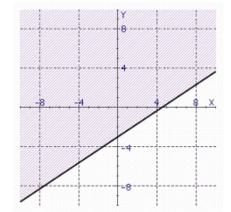
d.
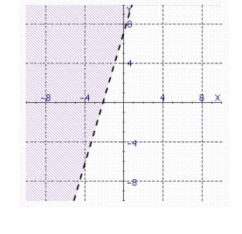
a.

b.

C.

d.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
44
Find the solution set of the system.
a.
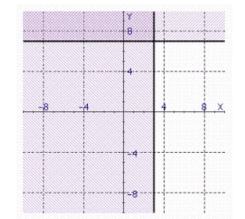
b.
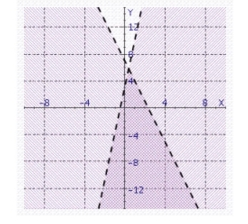
c.
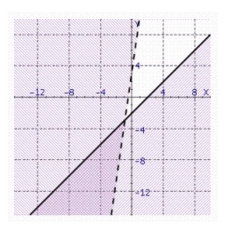
d.
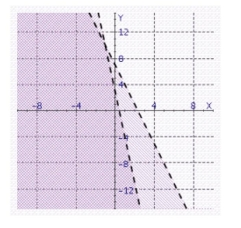
a.

b.

c.

d.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
45
Decompose the fraction into partial fractions.
a.
b.
c.
d.
e. none of these
a.
b.
c.
d.
e. none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
46
Decompose the fraction into partial fractions.
a.
b.
c.
d.
e. none of these
a.
b.
c.
d.
e. none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
47
A diet requires at least 26 units of vitamin C and at least 31 units of vitamin B complex.Two food supplements are available that provide these nutrients, in the amounts and costs shown in the table
Below.How much of each should be used to minimize the cost?
a. grams of and 5 grams of B: 62 cents
b. 5 grams of A and 2 grams of B: 32 cents
c. 5 grams of A and 7 grams of B: 58 cents
d. grams of and 9 grams of B: 54 cents
e. 1 gram of and 5 grams of cents
Below.How much of each should be used to minimize the cost?

a. grams of and 5 grams of B: 62 cents
b. 5 grams of A and 2 grams of B: 32 cents
c. 5 grams of A and 7 grams of B: 58 cents
d. grams of and 9 grams of B: 54 cents
e. 1 gram of and 5 grams of cents

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
48
Minimize subject to the given constraints.
a. at
b. at
c. at
d. at
e. none of these
a. at
b. at
c. at
d. at
e. none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
49
Which fraction appears in the partial fraction decomposition of ?
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
50
Find the graph of the linear inequality.
a.
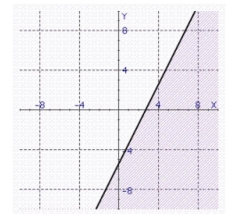
b.
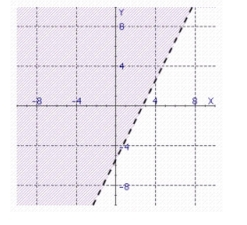
c.
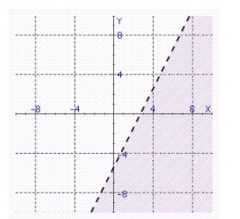
d.
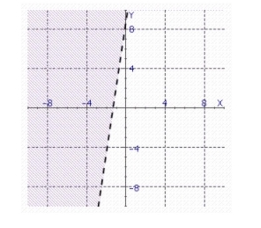
a.

b.

c.

d.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck


