Deck 7: Applications of Trigonometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/15
Play
Full screen (f)
Deck 7: Applications of Trigonometry
1
Find the magnitude of vector v.
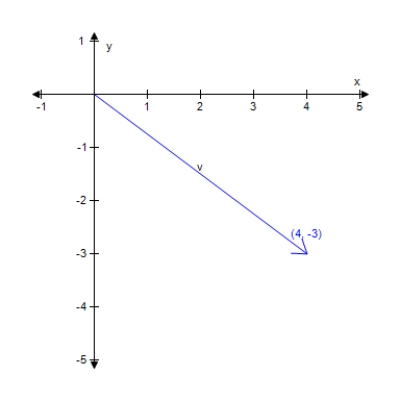

2
Find the angle between the vectors u and v. ,
3
Use the vectors , to find the indicated quantity. State whether the result is a vector or a scalar.
; vector
4
Given A = 10 , b = 10 and c = 8, use the Law of Sines to solve the triangle (if possible) for the value of c. If two solutions exist, find both. Round answer to two decimal places.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
5
Two ocean liners leave from the same port in Puerto Rico at 10:00 a.m. One travels at a bearing of N 50°W at 12 miles per hour, and the other travels at a bearing of S 53°W at 14 miles per hour. Approximate the distance between them at noon the same day. Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
6
A straight road makes an angle, A, of 16° with the horizontal. When the angle of elevation, B, of the sun is 59°, a vertical pole beside the road casts a shadow 7 feet long parallel to the road, see figure. Approximate the length of the pole. Round answer to two decimal places. 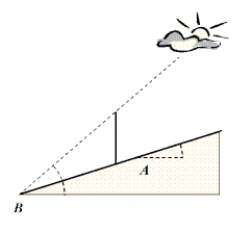


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
7
Use DeMoivre's theorem to find the indicated roots of the complex number.
Square roots of .
Square roots of .

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
8
Given a = 12, b = 11, and c = 10, use the Law of Cosines to solve the triangle for the value of B. Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
9
Divide the complex numbers below and leave the result in trigonometric form.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
10
Use vectors to find the measure of the angle at vertex B of triangle ABC, when , , and . Round answer to two decimal places.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
11
Use the law of Cosines to solve the given triangle. Round your answer to two decimal places.
a = 10, b = 5, C = 113°
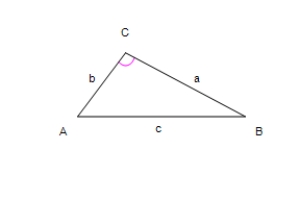
a = 10, b = 5, C = 113°


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
12
A 800-pound trailer is sitting on an exit ramp inclined at 33° on Highway 35. How much force is required to keep the trailer from rolling back down the exit ramp? Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
13
Find the fifth roots of the following complex number. Express the root(s) in trigonometric form.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
14
Find u + v.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
15
Given A = 33°, b = 13, and c = 7, use the Law of Cosines to solve the triangle for the value of a. Round your answer to two decimal places. 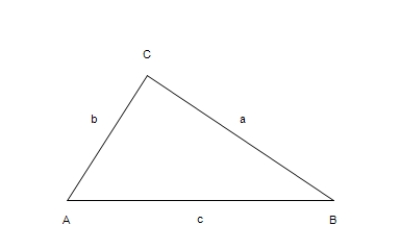 Figure not drawn to scale
Figure not drawn to scale
 Figure not drawn to scale
Figure not drawn to scale
Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck


