Deck 9: Systems of Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/117
Play
Full screen (f)
Deck 9: Systems of Equations
1
Classify the system as consistent or inconsistent, and dependent or independent.
x + 5y = 19 5x - 6y = 2
A) Inconsistent and independent
B) Consistent and independent
C) Consistent and dependent
D) Inconsistent and dependent
x + 5y = 19 5x - 6y = 2
A) Inconsistent and independent
B) Consistent and independent
C) Consistent and dependent
D) Inconsistent and dependent
B
2
Classify the system as consistent or inconsistent, and dependent or independent.
-3x = y + 3 6x - 2y = 3
A) Inconsistent and dependent
B) Consistent and independent
C) Inconsistent and independent
D) Consistent and dependent
-3x = y + 3 6x - 2y = 3
A) Inconsistent and dependent
B) Consistent and independent
C) Inconsistent and independent
D) Consistent and dependent
Inconsistent and independent
3
Solve using the substitution method.
x + y = 16 y = 3x + 4
A) (4, 12)
B) (2, 16)
C) (3, 13)
D) (13, 3)
x + y = 16 y = 3x + 4
A) (4, 12)
B) (2, 16)
C) (3, 13)
D) (13, 3)
C
4
Classify the system as consistent or inconsistent, and dependent or independent.
x + y = -11 x - y = -5
A) Inconsistent and independent
B) Inconsistent and dependent
C) Consistent and dependent
D) Consistent and independent
x + y = -11 x - y = -5
A) Inconsistent and independent
B) Inconsistent and dependent
C) Consistent and dependent
D) Consistent and independent

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
5
Solve graphically.
3x + 2y = 5 -6x - 4y = 5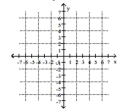
A) (1.5, -1)
B) No solution
C) (1, 1)
D) (-1.5, -1)
3x + 2y = 5 -6x - 4y = 5

A) (1.5, -1)
B) No solution
C) (1, 1)
D) (-1.5, -1)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
6
Solve graphically.
x = -y y + x = 6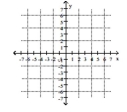
A) (1, 5)
B) No solution
C) (1, 1)
D) Infinite number of solutions
x = -y y + x = 6

A) (1, 5)
B) No solution
C) (1, 1)
D) Infinite number of solutions

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
7
Classify the system as consistent or inconsistent, and dependent or independent.
2x - 4y = 2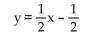
A) Consistent and dependent
B) Consistent and independent
C) Inconsistent and dependent
D) Inconsistent and independent
2x - 4y = 2
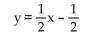
A) Consistent and dependent
B) Consistent and independent
C) Inconsistent and dependent
D) Inconsistent and independent

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
8
Classify the system as consistent or inconsistent, and dependent or independent.
-10x - 2y = 10 5x - y = -5
A) Consistent and independent
B) Inconsistent and independent
C) Inconsistent and dependent
D) Consistent and dependent
-10x - 2y = 10 5x - y = -5
A) Consistent and independent
B) Inconsistent and independent
C) Inconsistent and dependent
D) Consistent and dependent

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
9
Solve graphically.
3x + 4y = 31 4x - 2y = 34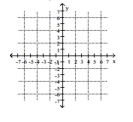
A) No solution
B) (1, 9)
C) (3, 22)
D) (9, 1)
3x + 4y = 31 4x - 2y = 34

A) No solution
B) (1, 9)
C) (3, 22)
D) (9, 1)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
10
Classify the system as consistent or inconsistent, and dependent or independent.
4x + 4y = 1 8x + 8y = 2
A) Inconsistent and dependent
B) Consistent and dependent
C) Inconsistent and independent
D) Consistent and independent
4x + 4y = 1 8x + 8y = 2
A) Inconsistent and dependent
B) Consistent and dependent
C) Inconsistent and independent
D) Consistent and independent

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
11
Solve graphically.
2x + y = -2 2x + 2y = 4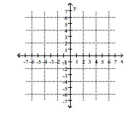
A) (4, 6)
B) (-4, 6)
C) (2, -6)
D) (-4, -5)
2x + y = -2 2x + 2y = 4

A) (4, 6)
B) (-4, 6)
C) (2, -6)
D) (-4, -5)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
12
Solve graphically.
x = -2 y = 1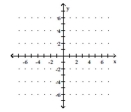
A) Infinitely many solutions
B) No solution
C) (-2, 1)
D) (1, -2)
x = -2 y = 1

A) Infinitely many solutions
B) No solution
C) (-2, 1)
D) (1, -2)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
13
Classify the system as consistent or inconsistent, and dependent or independent.
x - 8 = y y + 2 = x
A) Inconsistent and independent
B) Consistent and independent
C) Consistent and dependent
D) Inconsistent and dependent
x - 8 = y y + 2 = x
A) Inconsistent and independent
B) Consistent and independent
C) Consistent and dependent
D) Inconsistent and dependent

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
14
Solve using the substitution method.
y = 2x - 4 4x + y = -28
A) (-5, -14)
B) (-12, -4)
C) (-12, 20)
D) (-4, -12)
y = 2x - 4 4x + y = -28
A) (-5, -14)
B) (-12, -4)
C) (-12, 20)
D) (-4, -12)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
15
Solve graphically.
2x + y = 6 4x + 2y = 12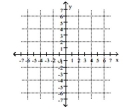
A) No solution
B) Infinite number of solutions
C) (0, 6)
D) (5, -4)
2x + y = 6 4x + 2y = 12

A) No solution
B) Infinite number of solutions
C) (0, 6)
D) (5, -4)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
16
Solve graphically.
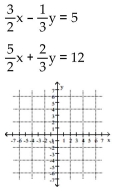
A) (4, -3)
B) (3, 4)
C) (4, 3)
D) (3, 1)

A) (4, -3)
B) (3, 4)
C) (4, 3)
D) (3, 1)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
17
Classify the system as consistent or inconsistent, and dependent or independent.
x + 6y = 17 2x + 12y = 34
A) Inconsistent and dependent
B) Consistent and dependent
C) Inconsistent and independent
D) Consistent and independent
x + 6y = 17 2x + 12y = 34
A) Inconsistent and dependent
B) Consistent and dependent
C) Inconsistent and independent
D) Consistent and independent

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
18
Classify the system as consistent or inconsistent, and dependent or independent.
x - 3y = 6 3y + 1 = x
A) Consistent and independent
B) Inconsistent and independent
C) Consistent and dependent
D) Inconsistent and dependent
x - 3y = 6 3y + 1 = x
A) Consistent and independent
B) Inconsistent and independent
C) Consistent and dependent
D) Inconsistent and dependent

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
19
Solve graphically.
3x - 2y = 4 -6x + 4y = 7
A) Infinite number of solutions
B) (2, 1)
C) No solution
D) (1, 2)
3x - 2y = 4 -6x + 4y = 7

A) Infinite number of solutions
B) (2, 1)
C) No solution
D) (1, 2)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
20
Classify the system as consistent or inconsistent, and dependent or independent.
x + y = 8 2x - 2y = 8
A) Inconsistent and dependent
B) Consistent and dependent
C) Consistent and independent
D) Inconsistent and independent
x + y = 8 2x - 2y = 8
A) Inconsistent and dependent
B) Consistent and dependent
C) Consistent and independent
D) Inconsistent and independent

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
21
Solve by the substitution method.
x + y = -1 x + y = 4
A) (0, 3)
B) No solution
C) (0, 0)
D) (-1, 4)
x + y = -1 x + y = 4
A) (0, 3)
B) No solution
C) (0, 0)
D) (-1, 4)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
22
Solve by the substitution method.
x + y = 7 5x + 5y = 35
A) (0, 0)
B) Infinite number of solutions
C) (7, 5)
D) (8, -1)
x + y = 7 5x + 5y = 35
A) (0, 0)
B) Infinite number of solutions
C) (7, 5)
D) (8, -1)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
23
Solve by the substitution method.
6x + 9y = 114 4x - 4y = -4
A) No solution
B) (7, 9)
C) (6, 9)
D) (7, 8)
6x + 9y = 114 4x - 4y = -4
A) No solution
B) (7, 9)
C) (6, 9)
D) (7, 8)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
24
Solve using the elimination method.
- x - 3y = - 2 -5x + 3y = -46
A) (8, -2)
B) No solution
C) (9, -3)
D) (2, 8)
- x - 3y = - 2 -5x + 3y = -46
A) (8, -2)
B) No solution
C) (9, -3)
D) (2, 8)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the problem.
The perimeter of a rectangle is 56 cm. One side is 12 cm longer than the other side. Find the lengths of the sides.
A) 8 cm, 20 cm
B) 11 cm, 23 cm
C) 8 cm, 12 cm
D) 16 cm, 28 cm
The perimeter of a rectangle is 56 cm. One side is 12 cm longer than the other side. Find the lengths of the sides.
A) 8 cm, 20 cm
B) 11 cm, 23 cm
C) 8 cm, 12 cm
D) 16 cm, 28 cm

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the problem.
The sum of two angles is 225°. One angle is 30° less than twice the other. Find the angles.
A) 136° and 89°
B) 85° and 140°
C) 83° and 142°
D) 83° and 136°
The sum of two angles is 225°. One angle is 30° less than twice the other. Find the angles.
A) 136° and 89°
B) 85° and 140°
C) 83° and 142°
D) 83° and 136°

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
27
Solve by the substitution method.
x - 5y = -27 -6x - 6y = -90
A) No solution
B) (-8, 8)
C) (7, 8)
D) (8, 7)
x - 5y = -27 -6x - 6y = -90
A) No solution
B) (-8, 8)
C) (7, 8)
D) (8, 7)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
28
Solve by the substitution method.
7x + 9y = -54 -3x - 4y = 24
A) (-1, -5)
B) (0, -5)
C) No solution
D) (0, -6)
7x + 9y = -54 -3x - 4y = 24
A) (-1, -5)
B) (0, -5)
C) No solution
D) (0, -6)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
29
Solve using the elimination method.
4 x - y = 19 5x + y = 35
A) (5, 6)
B) (6, 5)
C) (6, 6)
D) No solution
4 x - y = 19 5x + y = 35
A) (5, 6)
B) (6, 5)
C) (6, 6)
D) No solution

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
30
Solve by the substitution method.
8x + 17 = 9y -6x - 2y = 4
A) (-1, 2)
B) No solution
C) (-2, 2)
D) (-1, 1)
8x + 17 = 9y -6x - 2y = 4
A) (-1, 2)
B) No solution
C) (-2, 2)
D) (-1, 1)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.
The sum of two numbers is 34 and their difference is 12. Find the numbers.
A) 23 and 11
B) 25 and 37
C) 9 and 25
D) 11 and 23
The sum of two numbers is 34 and their difference is 12. Find the numbers.
A) 23 and 11
B) 25 and 37
C) 9 and 25
D) 11 and 23

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the problem.
The perimeter of a rectangle is 78 m. If the width were doubled and the length were increased by 12 m, the perimeter would be 132 m. What are the length and width of the rectangle?
A) width 19 m, length 19 m
B) width 14 m, length 19 m
C) width 15 m, length 24 m
D) width 24 m, length 15 m
The perimeter of a rectangle is 78 m. If the width were doubled and the length were increased by 12 m, the perimeter would be 132 m. What are the length and width of the rectangle?
A) width 19 m, length 19 m
B) width 14 m, length 19 m
C) width 15 m, length 24 m
D) width 24 m, length 15 m

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
33
Solve by the substitution method.
8x + 8y = -32 5x - 4y = -20
A) (-5, 1)
B) No solution
C) (-4, 0)
D) (-4, 1)
8x + 8y = -32 5x - 4y = -20
A) (-5, 1)
B) No solution
C) (-4, 0)
D) (-4, 1)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
34
Solve by the substitution method.
x + 6y = -1 7x + 7y = -7
A) (-1, 0)
B) (0, -1)
C) (1, -1)
D) No solution
x + 6y = -1 7x + 7y = -7
A) (-1, 0)
B) (0, -1)
C) (1, -1)
D) No solution

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
35
Solve by the substitution method.
x + 3y = 18 7x + 4y = 24
A) (0, 6)
B) No solution
C) (-6, 0)
D) (1, 5)
x + 3y = 18 7x + 4y = 24
A) (0, 6)
B) No solution
C) (-6, 0)
D) (1, 5)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
36
Solve using the substitution method.
x = 1 + -2y x + 2y = 8
A) Infinitely many solutions
B) (- 7, 15)
C) (- 7, - 15)
D) No solution
x = 1 + -2y x + 2y = 8
A) Infinitely many solutions
B) (- 7, 15)
C) (- 7, - 15)
D) No solution

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the problem.
Find two numbers whose sum is 40 and whose difference is 12.
A) 29 and 11
B) 26 and 14
C) 24 and 16
D) 16 and 28
Find two numbers whose sum is 40 and whose difference is 12.
A) 29 and 11
B) 26 and 14
C) 24 and 16
D) 16 and 28

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the problem.
Two angles have a sum of 81°. Their difference is 15°. Find the angles.
A) 67° and 14°
B) 35° and 50°
C) 48° and 33°
D) 46° and 35°
Two angles have a sum of 81°. Their difference is 15°. Find the angles.
A) 67° and 14°
B) 35° and 50°
C) 48° and 33°
D) 46° and 35°

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
39
Solve using the elimination method.
x + y = 11 x - y = 7
A) No solution
B) (9, 2)
C) (8, 3)
D) (-9, 3)
x + y = 11 x - y = 7
A) No solution
B) (9, 2)
C) (8, 3)
D) (-9, 3)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the problem.
The perimeter of a triangle is 65 cm. The triangle is isosceles now, but if its base were lengthened by 6 cm and each leg were shortened by 7 cm, it would be equilateral. Find the base of the original triangle.
A) 19 cm
B) 26 cm
C) 13 cm
D) 12 cm
The perimeter of a triangle is 65 cm. The triangle is isosceles now, but if its base were lengthened by 6 cm and each leg were shortened by 7 cm, it would be equilateral. Find the base of the original triangle.
A) 19 cm
B) 26 cm
C) 13 cm
D) 12 cm

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem using the elimination method.
There were 490 people at a play. The admission price was $3 for adults and $1 for children. The admission receipts were $1070. How many adults and how many children attended?
A) 290 adults and 200 children
B) 267 adults and 223 children
C) 100 adults and 390 children
D) 200 adults and 290 children
There were 490 people at a play. The admission price was $3 for adults and $1 for children. The admission receipts were $1070. How many adults and how many children attended?
A) 290 adults and 200 children
B) 267 adults and 223 children
C) 100 adults and 390 children
D) 200 adults and 290 children

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the system of equations by the elimination method.
x + 5y = 2 -4x + 6y = -8
A) (2, 0)
B) no solution
C) (3, 2)
D) (-2, -1)
x + 5y = 2 -4x + 6y = -8
A) (2, 0)
B) no solution
C) (3, 2)
D) (-2, -1)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the system of equations by the elimination method.
-0.8x + 0.4y = 4.8 0.1x - 0.1y = -0.7
A) (-50, 20)
B) (-0.5, 0.2)
C) (-5, 2)
D) (2, -5)
-0.8x + 0.4y = 4.8 0.1x - 0.1y = -0.7
A) (-50, 20)
B) (-0.5, 0.2)
C) (-5, 2)
D) (2, -5)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem using the elimination method.
A salesman sold $200 more than the rest of the sales staff. If the sales total for the day was $2050, how much did the rest of the sales staff sell?
A) $1125
B) $925
C) $1850
D) $1025
A salesman sold $200 more than the rest of the sales staff. If the sales total for the day was $2050, how much did the rest of the sales staff sell?
A) $1125
B) $925
C) $1850
D) $1025

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem using the elimination method.
A vendor sells hot dogs and bags of potato chips. A customer buys 2 hot dogs and 2 bags of potato chips for $5.00. Another customer buys 4 hot dogs and 3 bags of potato chips for $9.00. Find the cost of each item.
A) $1.75 for a hot dog; $1.25 for a bag of potato chips
B) $1.50 for a hot dog; $1.25 for a bag of potato chips
C) $1.00 for a hot dog; $1.50 for a bag of potato chips
D) $1.50 for a hot dog; $1.00 for a bag of potato chips
A vendor sells hot dogs and bags of potato chips. A customer buys 2 hot dogs and 2 bags of potato chips for $5.00. Another customer buys 4 hot dogs and 3 bags of potato chips for $9.00. Find the cost of each item.
A) $1.75 for a hot dog; $1.25 for a bag of potato chips
B) $1.50 for a hot dog; $1.25 for a bag of potato chips
C) $1.00 for a hot dog; $1.50 for a bag of potato chips
D) $1.50 for a hot dog; $1.00 for a bag of potato chips

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the system of equations by the elimination method.
-7x - 6y = -36 -3x + 4y = 24
A) no solution
B) (0, 7)
C) (0, 6)
D) (-1, 7)
-7x - 6y = -36 -3x + 4y = 24
A) no solution
B) (0, 7)
C) (0, 6)
D) (-1, 7)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the system of equations by the elimination method.
9x + 9y = -45 -4x - 6y = 20
A) (-5, 1)
B) no solution
C) (-5, 0)
D) (-6, 1)
9x + 9y = -45 -4x - 6y = 20
A) (-5, 1)
B) no solution
C) (-5, 0)
D) (-6, 1)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the system of equations by the elimination method.
3x - 5y = 2 18x - 30y = 12
A) (6, -10)
B) infinitely many solutions
C) (-10, 6)
D) no solution
3x - 5y = 2 18x - 30y = 12
A) (6, -10)
B) infinitely many solutions
C) (-10, 6)
D) no solution

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the system of equations by the elimination method.
2.5x + 0.3y = 10.6 0.5x + 0.9y = 3.8
A) (6.5, 2.3)
B) (4, 2)
C) (4.5, 2)
D) (1.5, 2.3)
2.5x + 0.3y = 10.6 0.5x + 0.9y = 3.8
A) (6.5, 2.3)
B) (4, 2)
C) (4.5, 2)
D) (1.5, 2.3)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem using the elimination method.
Two angles are supplementary, and one is 40° more than three times the other. Find the smaller angle.
A) 145°
B) 105°
C) 75°
D) 35°
Two angles are supplementary, and one is 40° more than three times the other. Find the smaller angle.
A) 145°
B) 105°
C) 75°
D) 35°

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the system of equations by the elimination method.
x - 3y = -5 4x - 4y = 12
A) (7, 4)
B) (6, 5)
C) no solution
D) (-7, 5)
x - 3y = -5 4x - 4y = 12
A) (7, 4)
B) (6, 5)
C) no solution
D) (-7, 5)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the system of equations by the elimination method.
x + 3y = 15 -6x + 4y = 20
A) no solution
B) (1, 4)
C) (-5, 0)
D) (0, 5)
x + 3y = 15 -6x + 4y = 20
A) no solution
B) (1, 4)
C) (-5, 0)
D) (0, 5)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem using the elimination method.
In a right triangle, one acute angle is 54° more than twice the other. Find each acute angle.
A) 12° and 78°
B) 37° and 53°
C) 21° and 69°
D) 28° and 62°
In a right triangle, one acute angle is 54° more than twice the other. Find each acute angle.
A) 12° and 78°
B) 37° and 53°
C) 21° and 69°
D) 28° and 62°

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the system of equations by the elimination method.
5x - 6y = -5 15x - 18y = 15
A) no solution
B) (25, -30)
C) infinitely many solutions
D) (-25, 30)
5x - 6y = -5 15x - 18y = 15
A) no solution
B) (25, -30)
C) infinitely many solutions
D) (-25, 30)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem using the elimination method.
There were 38,000 people at a ball game in Los Angeles. The day's receipts were $229,000. How many people paid $11 for reserved seats and how many paid $4 for general admission?
A) 19,250 paid $11 and 18,750 paid $4
B) 27,000 paid $11 and 11,000 paid $4
C) 18,750 paid $11 and 19,250 paid $4
D) 11,000 paid $11 and 27,000 paid $4
There were 38,000 people at a ball game in Los Angeles. The day's receipts were $229,000. How many people paid $11 for reserved seats and how many paid $4 for general admission?
A) 19,250 paid $11 and 18,750 paid $4
B) 27,000 paid $11 and 11,000 paid $4
C) 18,750 paid $11 and 19,250 paid $4
D) 11,000 paid $11 and 27,000 paid $4

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the system of equations by the elimination method.
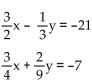
A) (-12, 9)
B) (12, 9)
C) (-12, -9)
D) (9, -12)
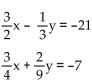
A) (-12, 9)
B) (12, 9)
C) (-12, -9)
D) (9, -12)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the system of equations by the elimination method.
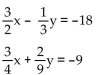
A) (-12, 0)
B) (0, -12)
C) (0, 12)
D) (12, 0)
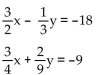
A) (-12, 0)
B) (0, -12)
C) (0, 12)
D) (12, 0)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the problem using the elimination method.
Two angles are supplementary, and one is 5° more than six times the other. Find the larger angle.
A) 25°
B) 155°
C) 70°
D) 110°
Two angles are supplementary, and one is 5° more than six times the other. Find the larger angle.
A) 25°
B) 155°
C) 70°
D) 110°

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
59
Solve using the elimination method.
x + 6y = 26 2x + 6y = 22
A) (4, 4)
B) No solution
C) (-4, 5)
D) (-3, -4)
x + 6y = 26 2x + 6y = 22
A) (4, 4)
B) No solution
C) (-4, 5)
D) (-3, -4)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the system of equations by the elimination method.
0.3x + 0.5y = 3.1 x - 0.1y = 1.5
A) (0.2, 0.5)
B) (5, 2)
C) no solution
D) (2, 5)
0.3x + 0.5y = 3.1 x - 0.1y = 1.5
A) (0.2, 0.5)
B) (5, 2)
C) no solution
D) (2, 5)

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
Anne and Nancy use a metal alloy that is 16% copper to make jewelry. How many ounces of an alloy that is 10% copper must be mixed with an alloy that is 20% copper to form 55 ounces of the desired alloy?
A) 22 ounces
B) 33 ounces
C) 38 ounces
D) 24 ounces
Anne and Nancy use a metal alloy that is 16% copper to make jewelry. How many ounces of an alloy that is 10% copper must be mixed with an alloy that is 20% copper to form 55 ounces of the desired alloy?
A) 22 ounces
B) 33 ounces
C) 38 ounces
D) 24 ounces

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the problem.
How many liters of a 20% alcohol solution must be mixed with 90 liters of a 80% solution to get a 40% solution?
A) 27 L
B) 18 L
C) 180 L
D) 270 L
How many liters of a 20% alcohol solution must be mixed with 90 liters of a 80% solution to get a 40% solution?
A) 27 L
B) 18 L
C) 180 L
D) 270 L

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the problem.
Mardi received an inheritance of $60,000. She invested part at 8% and deposited the remainder in tax-free bonds at 11%. Her total annual income from the investments was $5700. Find the amount invested at 8%.
A) $54,300
B) $29,000
C) $30,000
D) $15,000
Mardi received an inheritance of $60,000. She invested part at 8% and deposited the remainder in tax-free bonds at 11%. Her total annual income from the investments was $5700. Find the amount invested at 8%.
A) $54,300
B) $29,000
C) $30,000
D) $15,000

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
64
Solve.
A cruise boat travels 48 miles downstream in 3 hours and returns to its starting point upstream in 12 hours. Find the speed of the stream.
A) 16 mph
B) 10 mph
C) 6 mph
D) 26 mph
A cruise boat travels 48 miles downstream in 3 hours and returns to its starting point upstream in 12 hours. Find the speed of the stream.
A) 16 mph
B) 10 mph
C) 6 mph
D) 26 mph

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem using the elimination method.
In a basketball game, Will scored 40 points, consisting only of three-point shots and two-point shots. He made a total of 17 shots. How many shots of each type did he make?
A) two-point shots: 11; three-point shots: 6
B) two-point shots: 6; three-point shots: 11
C) two-point shots: 10; three-point shots: 7
D) two-point shots: 12; three-point shots: 5
In a basketball game, Will scored 40 points, consisting only of three-point shots and two-point shots. He made a total of 17 shots. How many shots of each type did he make?
A) two-point shots: 11; three-point shots: 6
B) two-point shots: 6; three-point shots: 11
C) two-point shots: 10; three-point shots: 7
D) two-point shots: 12; three-point shots: 5

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem using the elimination method.
The sum of two numbers is 41. The larger number minus the smaller number is 9. What are the numbers?
A) 18 and 27
B) 25 and 16
C) 33 and 8
D) 23 and 18
The sum of two numbers is 41. The larger number minus the smaller number is 9. What are the numbers?
A) 18 and 27
B) 25 and 16
C) 33 and 8
D) 23 and 18

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the problem.
Tim and Judy mix two kinds of feed for pedigreed dogs. They wish to make 28 pounds of feed worth $0.62 per pound by mixing one kind worth $0.15 per pound with another worth $0.97 per pound. How many pounds of
The cheaper kind should they use in the mix?
A) 21 pounds
B) 14 pounds
C) 12 pounds
D) 16 pounds
Tim and Judy mix two kinds of feed for pedigreed dogs. They wish to make 28 pounds of feed worth $0.62 per pound by mixing one kind worth $0.15 per pound with another worth $0.97 per pound. How many pounds of
The cheaper kind should they use in the mix?
A) 21 pounds
B) 14 pounds
C) 12 pounds
D) 16 pounds

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the problem.
Walt made an extra $10,000 last year from a part-time job. He invested part of the money at 10% and the rest at 9%. He made a total of $960 in interest. How much was invested at 9%?
A) $8000
B) $5000
C) $6000
D) $4000
Walt made an extra $10,000 last year from a part-time job. He invested part of the money at 10% and the rest at 9%. He made a total of $960 in interest. How much was invested at 9%?
A) $8000
B) $5000
C) $6000
D) $4000

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the problem using the elimination method.
The sum of two numbers is 100. The second number is three times as large as the first number. What are the numbers?
A) 22 and 78
B) 23 and 69
C) 23 and 77
D) 25 and 75
The sum of two numbers is 100. The second number is three times as large as the first number. What are the numbers?
A) 22 and 78
B) 23 and 69
C) 23 and 77
D) 25 and 75

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
A woman made a deposit of $267. If her deposit consisted of 91 bills, some of them one-dollar bills and the rest being five-dollar bills, how many one-dollar bills did she deposit?
A) 44 one-dollars
B) 42 one-dollars
C) 37 one-dollars
D) 47 one-dollars
A woman made a deposit of $267. If her deposit consisted of 91 bills, some of them one-dollar bills and the rest being five-dollar bills, how many one-dollar bills did she deposit?
A) 44 one-dollars
B) 42 one-dollars
C) 37 one-dollars
D) 47 one-dollars

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.
A sum of money amounting to $3.45 consists of dimes and quarters. If there are 18 coins in all, how many are quarters?
A) 16 quarters
B) 7 quarters
C) 11 quarters
D) 9 quarters
A sum of money amounting to $3.45 consists of dimes and quarters. If there are 18 coins in all, how many are quarters?
A) 16 quarters
B) 7 quarters
C) 11 quarters
D) 9 quarters

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the problem using the elimination method.
The sum of two numbers is 4. Three times the larger number plus two times the smaller number is 37. Find the numbers.
A) 25 and -21
B) 33 and -29
C) 29 and -25
D) 25 and -29
The sum of two numbers is 4. Three times the larger number plus two times the smaller number is 37. Find the numbers.
A) 25 and -21
B) 33 and -29
C) 29 and -25
D) 25 and -29

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
Ron and Kathy are ticket-sellers at their class play, Ron handling student tickets that sell for $3.00 each and Kathy selling adult tickets for $5.50 each. If their total income for 25 tickets was $120.00, how many did Ron sell?
A) 23 tickets
B) 18 tickets
C) 7 tickets
D) 9 tickets
Ron and Kathy are ticket-sellers at their class play, Ron handling student tickets that sell for $3.00 each and Kathy selling adult tickets for $5.50 each. If their total income for 25 tickets was $120.00, how many did Ron sell?
A) 23 tickets
B) 18 tickets
C) 7 tickets
D) 9 tickets

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the problem.
A merchant has coffee worth $20 a pound that she wishes to mix with 90 pounds of coffee worth $90 a pound to get a mixture that can be sold for $80 a pound. How many pounds of the $20 coffee should be used?
A) 7.5 lb
B) 52.5 lb
C) 105 lb
D) 15 lb
A merchant has coffee worth $20 a pound that she wishes to mix with 90 pounds of coffee worth $90 a pound to get a mixture that can be sold for $80 a pound. How many pounds of the $20 coffee should be used?
A) 7.5 lb
B) 52.5 lb
C) 105 lb
D) 15 lb

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the problem.
There were 670 people at a play. The admission price was $2 for adults and $1 for children. The admission receipts were $1020. How many adults and how many children attended?
A) 320 adults and 350 children
B) 255 adults and 415 children
C) 350 adults and 320 children
D) 160 adults and 510 children
There were 670 people at a play. The admission price was $2 for adults and $1 for children. The admission receipts were $1020. How many adults and how many children attended?
A) 320 adults and 350 children
B) 255 adults and 415 children
C) 350 adults and 320 children
D) 160 adults and 510 children

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the problem.
Mrs. Boyd has a desk full of quarters and nickels. If she has a total of 28 coins with a total face value of $5.00, how many of the coins are nickels?
A) 23 nickels
B) 10 nickels
C) 12 nickels
D) 18 nickels
Mrs. Boyd has a desk full of quarters and nickels. If she has a total of 28 coins with a total face value of $5.00, how many of the coins are nickels?
A) 23 nickels
B) 10 nickels
C) 12 nickels
D) 18 nickels

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the problem.
A contractor mixes concrete from bags of pre-mix for small jobs. How many bags with 9% cement should he mix with 10 bags of 10.8% cement to produce a mix containing 10% cement?
A) 23 bags
B) 10 bags
C) 8 bags
D) 18 bags
A contractor mixes concrete from bags of pre-mix for small jobs. How many bags with 9% cement should he mix with 10 bags of 10.8% cement to produce a mix containing 10% cement?
A) 23 bags
B) 10 bags
C) 8 bags
D) 18 bags

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the problem.
Ellen wishes to mix candy worth $1.79 per pound with candy worth $3.75 per pound to form 22 pounds of a mixture worth $2.95 per pound. How many pounds of the more expensive candy should she use?
A) 13 pounds
B) 11 pounds
C) 9 pounds
D) 18 pounds
Ellen wishes to mix candy worth $1.79 per pound with candy worth $3.75 per pound to form 22 pounds of a mixture worth $2.95 per pound. How many pounds of the more expensive candy should she use?
A) 13 pounds
B) 11 pounds
C) 9 pounds
D) 18 pounds

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the problem.
In a chemistry class, 6 liters of a 4% silver iodide solution must be mixed with a 10% solution to get a 6% solution. How many liters of the 10% solution are needed?
A) 4.0 L
B) 3.0 L
C) 2.0 L
D) 6.0 L
In a chemistry class, 6 liters of a 4% silver iodide solution must be mixed with a 10% solution to get a 6% solution. How many liters of the 10% solution are needed?
A) 4.0 L
B) 3.0 L
C) 2.0 L
D) 6.0 L

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the problem.
Andy has 33 coins made up of quarters and half dollars, and their total value is $13.25. How many quarters does he have?
A) 18 quarters
B) 22 quarters
C) 20 quarters
D) 13 quarters
Andy has 33 coins made up of quarters and half dollars, and their total value is $13.25. How many quarters does he have?
A) 18 quarters
B) 22 quarters
C) 20 quarters
D) 13 quarters

Unlock Deck
Unlock for access to all 117 flashcards in this deck.
Unlock Deck
k this deck


