Deck 11: Multiple Regression
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/58
Play
Full screen (f)
Deck 11: Multiple Regression
1
If our regression equation is Ŷ = 0.75 × age 0.50 × experience - 0.10 × grade point average - 2.0, and if our first subject had scores of 16, 4, and 3.0 on those three variables, respectively, then that subject's predicted score would be
A) 11.7
B) 10
C) 16
D) -3
A) 11.7
B) 10
C) 16
D) -3
11.7
2
The multiple correlation of several variables with a dependent variable is
A) less than the largest individual correlation.
B) equal to the correlation of the dependent variable to the values predicted by the regression equation.
C) noticeably less than the correlation of the dependent variable to the values predicted by the regression equation.
D) It could take on any value.
A) less than the largest individual correlation.
B) equal to the correlation of the dependent variable to the values predicted by the regression equation.
C) noticeably less than the correlation of the dependent variable to the values predicted by the regression equation.
D) It could take on any value.
equal to the correlation of the dependent variable to the values predicted by the regression equation.
3
In simple correlation a squared correlation coefficient tells us the percentage of variability in Y associated with variability in X . In multiple regression, the squared multiple correlation coefficient
A) has the same kind of meaning.
B) has no meaning.
C) overestimates the degree of variance accounted for.
D) underestimates the degree of variance accounted for.
A) has the same kind of meaning.
B) has no meaning.
C) overestimates the degree of variance accounted for.
D) underestimates the degree of variance accounted for.
has the same kind of meaning.
4
If one independent variable has a larger coefficient than another, this means
A) that the variable with the larger coefficient is a more important predictor.
B) that the variable with the larger coefficient is a more statistically significant predictor.
C) that the variable with the larger coefficient contributes more to predicting the variability in the criterion.
D) We can't say anything about relative importance or significance from what is given here.
A) that the variable with the larger coefficient is a more important predictor.
B) that the variable with the larger coefficient is a more statistically significant predictor.
C) that the variable with the larger coefficient contributes more to predicting the variability in the criterion.
D) We can't say anything about relative importance or significance from what is given here.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
5
If you have a number of scores that are outliers you should
A) throw them out.
B) run the analysis with and without them, to see what difference they make.
C) try to identify what is causing those scores to be outliers.
D) both b and c
A) throw them out.
B) run the analysis with and without them, to see what difference they make.
C) try to identify what is causing those scores to be outliers.
D) both b and c

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
6
If two variables taken together account for 65% of the variability in Y , and a third variable has a simple squared correlation with Y of .10, then adding that variable to the equation will allow us to account for
A) 65% of the variability in Y .
B) 75% of the variability in Y .
C) 10% of the variability in Y .
D) at least 65% of the variability in Y .
A) 65% of the variability in Y .
B) 75% of the variability in Y .
C) 10% of the variability in Y .
D) at least 65% of the variability in Y .

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
7
If we want to compare the contribution of several predictors to the prediction of a dependent variable, we can get at least a rough idea by comparing
A) the regression coefficients.
B) the standardized regression coefficients.
C) the variances of the several variables.
D) the simple Pearson correlations of each variable with the dependent variable.
A) the regression coefficients.
B) the standardized regression coefficients.
C) the variances of the several variables.
D) the simple Pearson correlations of each variable with the dependent variable.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
8
If we find all of the residuals when predicting our obtained values of Y from the regression equation, the sum of squared residuals would be expected to be _______ the sum of the squared residuals for a new set of data.
A) less than
B) greater than
C) the same as
D) We can't tell.
A) less than
B) greater than
C) the same as
D) We can't tell.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
9
In the previous question, a student who scored 0 on both X 1 and X 2 would be expected to have a dependent variable score of
A) 0.
B) 3.5.
C) 12.
D) the mean of Y .
A) 0.
B) 3.5.
C) 12.
D) the mean of Y .

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
10
If we have three predictors and they are all individually correlated with the dependent variable, we know that
A) each of them will play a significant role in the regression equation.
B) each of them must be correlated with each other.
C) each regression coefficient will be significantly different from zero.
D) none of the above
A) each of them will play a significant role in the regression equation.
B) each of them must be correlated with each other.
C) each regression coefficient will be significantly different from zero.
D) none of the above

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
11
In multiple regression an outlier is one that
A) is reasonably close to the regression surface.
B) is far from the regression surface.
C) is extreme on at least one variable.
D) will necessarily influence the final result in an important way.
A) is reasonably close to the regression surface.
B) is far from the regression surface.
C) is extreme on at least one variable.
D) will necessarily influence the final result in an important way.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
12
Before running a multiple regression, it is smart to look at the distribution of each variable. We do this because
A) we want to see that the distributions are not very badly skewed.
B) we want to look for extreme scores.
C) we want to pick up obvious coding errors.
D) all of the above
A) we want to see that the distributions are not very badly skewed.
B) we want to look for extreme scores.
C) we want to pick up obvious coding errors.
D) all of the above

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
13
The difference between multiple regression and simple regression is that
A) multiple regression can have more than one dependent variable.
B) multiple regression can have more than one independent variable.
C) multiple regression does not produce a correlation coefficient.
D) both b and c
A) multiple regression can have more than one dependent variable.
B) multiple regression can have more than one independent variable.
C) multiple regression does not produce a correlation coefficient.
D) both b and c

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
14
When we speak of the correlations among the independent variables, we are speaking of
A) homoscedasticity.
B) multicollinearity.
C) independence.
D) multiple correlation.
A) homoscedasticity.
B) multicollinearity.
C) independence.
D) multiple correlation.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
15
If two variables are each correlated significantly with the dependent variable, then the multiple correlation will be
A) the sum of the two correlations.
B) the sum of the two correlations squared.
C) no less than the larger of the two individual correlations.
D) It could take on any value.
A) the sum of the two correlations.
B) the sum of the two correlations squared.
C) no less than the larger of the two individual correlations.
D) It could take on any value.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
16
Assume that we generated a prediction just by adding together the number of stressful events you report experiencing over the last month, the number of close friends you have, and your score on a measure assessing how much control you feel you have over events in your life (i.e., prediction = stress + friends + control). The regression coefficient for stressful events would be
A) 1.0
B) 4.0
C) 0.0
D) There is no way to know.
A) 1.0
B) 4.0
C) 0.0
D) There is no way to know.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
17
Given the following regression equation ( Ŷ = 3.5 X 1 + 2 X 2 + 12), the coefficient for X 1 would mean that
A) two people who differ by one point on X 1 would differ by 3.5 points on Ŷ .
B) two people who differ by one point on X 1 would differ by 3.5 points on Ŷ , assuming that they did not differ on X 2.
C) X 1 causes a 3.5 unit change in the dependent variable.
D) X 1 is more important than X 2.
A) two people who differ by one point on X 1 would differ by 3.5 points on Ŷ .
B) two people who differ by one point on X 1 would differ by 3.5 points on Ŷ , assuming that they did not differ on X 2.
C) X 1 causes a 3.5 unit change in the dependent variable.
D) X 1 is more important than X 2.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
18
In multiple regression the intercept is usually denoted as
A) a
B) b1
C) b0
D) 0
A) a
B) b1
C) b0
D) 0

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose that in the previous question another subject had a predicted score of 10.3, and actually obtained a score of 12.4. For this subject the residual score would be
A) 2.1
B) -0.7
C) 12.4
D) 0.0
A) 2.1
B) -0.7
C) 12.4
D) 0.0

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
20
In the previous question the intercept would be
A) 1.0
B) 0.0
C) 3.0
D) There would be no way to know.
A) 1.0
B) 0.0
C) 3.0
D) There would be no way to know.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
21
We want to predict a person's happiness from the following variables: degree of optimism, success in school, and number of close friends. What type of statistical test can tell us whether these variables predict a person's happiness?
A) factorial ANOVA
B) multiple comparison
C) regression
D) multiple regression
A) factorial ANOVA
B) multiple comparison
C) regression
D) multiple regression

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
22
The text generally recommended against formal procedures for finding an optimal regression procedure because
A) those procedures don't work.
B) those procedures pay too much attention to chance differences.
C) the statistical software won't handle those procedures.
D) all of the above
A) those procedures don't work.
B) those procedures pay too much attention to chance differences.
C) the statistical software won't handle those procedures.
D) all of the above

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
23
Multicollinearity occurs when the predictor variables are highly correlated with one another.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
24
The example in Chapter 11 of predicting weight from height and sex showed that
A) adding sex as a predictor accounted for an important source of variability.
B) there is a much stronger relationship between height and weight in males than in females.
C) sex is not a useful predictor in this situation.
D) we cannot predict very well, even with two predictors.
A) adding sex as a predictor accounted for an important source of variability.
B) there is a much stronger relationship between height and weight in males than in females.
C) sex is not a useful predictor in this situation.
D) we cannot predict very well, even with two predictors.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
25
If we predict anxiety from stress and intrusive thoughts, and if the multiple regression is significant, that means that
A) the regression coefficient for stress will be significant.
B) the regression coefficient for intrusive thoughts will be significant.
C) both variables will be significant predictors.
D) We can't tell.
A) the regression coefficient for stress will be significant.
B) the regression coefficient for intrusive thoughts will be significant.
C) both variables will be significant predictors.
D) We can't tell.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
26
Multiple regression analysis yielded the following regression equation:
Predicted Happiness = .36 × friends - .13 × s tress + 1.23
Which of the following is true?
A) Happiness increases as Friends increase.
B) Happiness increases as Stress increases.
C) Happiness decreases as Friends and Stress increase.
D) none of the above
Predicted Happiness = .36 × friends - .13 × s tress + 1.23
Which of the following is true?
A) Happiness increases as Friends increase.
B) Happiness increases as Stress increases.
C) Happiness decreases as Friends and Stress increase.
D) none of the above

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
27
If you drop a predictor from the regression equation
A) the correlation could increase.
B) the correlation will probably go down.
C) the correlation could stay the same.
D) both b and c
A) the correlation could increase.
B) the correlation will probably go down.
C) the correlation could stay the same.
D) both b and c

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
28
Multiple regression means there is more than one criterion variable.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
29
If the multiple correlation is high, we would expect to have _______ residuals than if the multiple correlation is low.
A) smaller
B) larger
C) the same as
D) We can't tell.
A) smaller
B) larger
C) the same as
D) We can't tell.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
30
The example in the text predicting distress in cancer patients used distress at an earlier time as one of the predictors. This was done
A) because the authors wanted to be able to report a large correlation.
B) because the authors wanted to see what effect earlier distress had.
C) because the authors wanted to look at the effects of self-blame after controlling for initial differences in distress.
D) because the authors didn't care about self-blame, but wanted to control for it.
A) because the authors wanted to be able to report a large correlation.
B) because the authors wanted to see what effect earlier distress had.
C) because the authors wanted to look at the effects of self-blame after controlling for initial differences in distress.
D) because the authors didn't care about self-blame, but wanted to control for it.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
31
In an example in Chapter 10 we found that the relationship between how a student evaluated a course, and that student's expected grade was significant. In this chapter Grade was not a significant predictor. The difference is
A) we had a new set of data.
B) grade did not predict significantly once the other predictors were taken into account.
C) the other predictors were correlated with grade.
D) both b and c
A) we had a new set of data.
B) grade did not predict significantly once the other predictors were taken into account.
C) the other predictors were correlated with grade.
D) both b and c

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
32
Many of the procedures for finding an optimal regression equation (whatever that means) are known as
A) hunting procedures.
B) trial and error procedures.
C) trialwise procedures.
D) stepwise procedures.
A) hunting procedures.
B) trial and error procedures.
C) trialwise procedures.
D) stepwise procedures.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
33
The following regression equation was found for a sample of college students. predicted happiness = 32.8 GPA + 17.3 × pocket money + 7.4
Which of the following can be concluded?
A) The correlation between pocket money and happiness is larger than the correlation between GPA and happiness.
B) GPA is less useful than pocket money in predicting happiness.
C) For students with no pocket money, a one-unit increase in GPA will increase the value of predicted happiness by 32.8 units.
D) The r-squared value for GPA must be greater than the r-squared value for pocket money.
Which of the following can be concluded?
A) The correlation between pocket money and happiness is larger than the correlation between GPA and happiness.
B) GPA is less useful than pocket money in predicting happiness.
C) For students with no pocket money, a one-unit increase in GPA will increase the value of predicted happiness by 32.8 units.
D) The r-squared value for GPA must be greater than the r-squared value for pocket money.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
34
A multiple regression analysis was used to test the values of visual acuity, swing power, and cost of clubs for predicting golf scores. The regression analysis showed that visual acuity and swing power predicted significant amounts of the variability in golf scores, but cost of clubs did not. What can be concluded from these results?
A) Cost of clubs and golf scores are not correlated.
B) Cost of clubs adds predictive value above and beyond the predictive value of visual acuity and swing power.
C) The regression coefficient of cost of clubs is equal to zero.
D) Removing cost of clubs from the overall model will not reduce the model's R2 value significantly.
A) Cost of clubs and golf scores are not correlated.
B) Cost of clubs adds predictive value above and beyond the predictive value of visual acuity and swing power.
C) The regression coefficient of cost of clubs is equal to zero.
D) Removing cost of clubs from the overall model will not reduce the model's R2 value significantly.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
35
The statistical tests on regression coefficients are usually
A) t tests.
B) z tests.
C) F tests.
D) r tests.
A) t tests.
B) z tests.
C) F tests.
D) r tests.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
36
When testing null hypotheses about multiple regression we
A) only look at the significance test on the overall multiple correlation.
B) have a separate significance test for each predictor and for overall significance.
C) don't have to worry about significance testing.
D) know that if one predictor is significant, the others won't be.
A) only look at the significance test on the overall multiple correlation.
B) have a separate significance test for each predictor and for overall significance.
C) don't have to worry about significance testing.
D) know that if one predictor is significant, the others won't be.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
37
If we know that a regression coefficient is statistically significant, we know that
A) it is positive.
B) it is not 0.0.
C) it is not 1.0.
D) it is large.
A) it is positive.
B) it is not 0.0.
C) it is not 1.0.
D) it is large.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
38
The Analysis of Variance section in computer results for multiple regression
A) compares the means of several variables.
B) tests the overall significance of the regression.
C) tests the significance of each predictor.
D) compares the variances of the variables.
A) compares the means of several variables.
B) tests the overall significance of the regression.
C) tests the significance of each predictor.
D) compares the variances of the variables.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
39
A table in which each variable is correlated with every other variable is called
A) a multivariate table
B) an intercorrelation matrix
C) a contingency table
D) a pattern matrix
A) a multivariate table
B) an intercorrelation matrix
C) a contingency table
D) a pattern matrix

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
40
If the overall analysis of variance is NOT significant
A) we need to look particularly closely at the tests on the individual variables.
B) it probably doesn't make much sense to look at the individual variables.
C) the multiple correlation is too large to worry about.
D) none of the above
A) we need to look particularly closely at the tests on the individual variables.
B) it probably doesn't make much sense to look at the individual variables.
C) the multiple correlation is too large to worry about.
D) none of the above

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
41
Individual predictors cannot be individually associated with the criterion variable if R is not different from 0 (i.e., if the entire model is not significant).

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
42
Multiple regression examines the degree of association between any predictor and the criterion variable controlling for other predictors in the equation.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
43
In a regression predicting adolescent delinquent behavior from gender, the number of delinquent peers in the social network, and parental under control, R2 = .60. This means each of the variables accounted for 36% of the variability in delinquent behavior.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
44
Any association that was significant as a simple correlation will be significant in a multiple regression equation predicting the same criterion variable.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
45
If you wanted to identify mothers who needed a parenting intervention to enhance sensitivity and could only collect two pieces of information from each family due to time and costs, which of the measures in the previous example would you select? Why?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
46
Are the set of predictors significantly associated with maternal sensitivity?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
47
Given the information in the following table, create the corresponding regression equation.
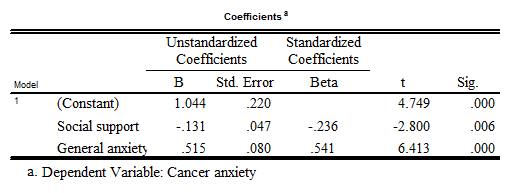


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
48
In multiple regression, the criterion variable is predicted by more than one independent variable.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
49
Based on the previous regression equation you just created, estimate cancer anxiety given the following values.
a. social support = 100; general anxiety = 50
b. social support = 25; general anxiety = 7
a. social support = 100; general anxiety = 50
b. social support = 25; general anxiety = 7

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
50
Stepwise regression procedures capitalize on chance.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
51
Which individual predictors are significantly associated with maternal sensitivity?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
52
Multiple regression allows you to examine the degree of association between individual independent variables and the criterion variable AND the degree of association between the set of independent variables and the criterion variable.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
53
Based on the same formula ( Ŷ = .75 X -.40 Z + 5), calculate the missing predictor variables based on the following information.
a. Ŷ = 100; X = 0
b. Ŷ = 0; Z = -20
a. Ŷ = 100; X = 0
b. Ŷ = 0; Z = -20

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
54
R2 can range from -1 to 1.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
55
Write a sentence explaining the analysis presented in the following table (i.e., what are the predictor variables, what is the criterion variable).
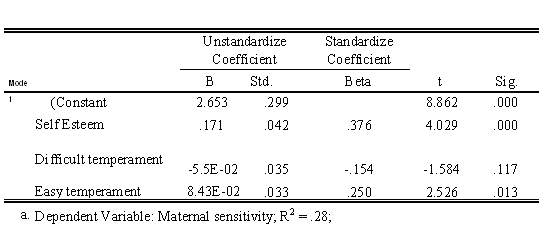


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
56
Estimate Y based on the equation Ŷ = .75 X -.40 Z + 5 using the following values.
a. X = 10; Z = 0
b. X = 0; Z = 0
c. X = 20; Z = 100
a. X = 10; Z = 0
b. X = 0; Z = 0
c. X = 20; Z = 100

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
57
How much variability in maternal sensitivity is accounted for by the set of predictors?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
58
How do the regression results vary from the simple correlations presented below?
Explain why this may be the case.

Explain why this may be the case.


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck


