Deck 5: Further Applications of the Derivative
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/85
Play
Full screen (f)
Deck 5: Further Applications of the Derivative
1
Find the exact location of all relative and absolute extrema of the function 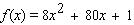 with domain -6, 6 .
with domain -6, 6 .
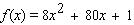 with domain -6, 6 .
with domain -6, 6 .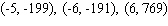
2
Maximize 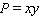 with
with 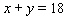 .
.
A)P = 18
B)P = 9
C)P = 81
D)P = -81
E)P = 6,561
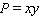 with
with 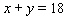 .
.A)P = 18
B)P = 9
C)P = 81
D)P = -81
E)P = 6,561
P = 81
3
For a rectangle with area 81 to have the smallest perimeter, what dimensions should it have?
A)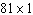
B)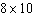
C)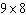
D)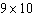
E)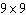
A)
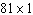
B)
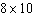
C)
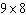
D)
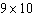
E)
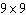
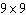
4
The graph of the derivative of a function f is shown. Determine the x -coordinates of all stationary and singular points of f . (Assume that f ( x )is defined and continuous everywhere in -10, 10 .) 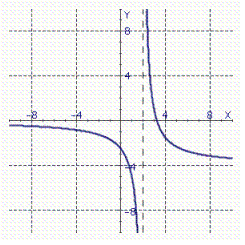 Please enter your answer in the form x = a , x = b , ... where a, b, ... are the x -coordinates of stationary or singular points of f .
Please enter your answer in the form x = a , x = b , ... where a, b, ... are the x -coordinates of stationary or singular points of f .
 Please enter your answer in the form x = a , x = b , ... where a, b, ... are the x -coordinates of stationary or singular points of f .
Please enter your answer in the form x = a , x = b , ... where a, b, ... are the x -coordinates of stationary or singular points of f .
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
5
Hercules films is deciding on the price of the video release of its film Son of Frankenstein . Its marketing people estimate that at a price of p dollars, it can sell a total of 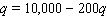 copies. What price will bring in the greatest revenue?
copies. What price will bring in the greatest revenue?
A)$77.25
B)$24.50
C)$25.00
D)$25.75
E)$37.50
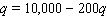 copies. What price will bring in the greatest revenue?
copies. What price will bring in the greatest revenue?A)$77.25
B)$24.50
C)$25.00
D)$25.75
E)$37.50

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
6
Minimize 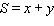 with
with 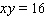 and both
and both 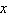 and
and 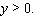
A)S = 16
B)S = 4
C)S = -8
D)S = 6
E)S = 8
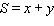 with
with 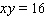 and both
and both 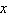 and
and 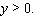
A)S = 16
B)S = 4
C)S = -8
D)S = 6
E)S = 8

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
7
For a rectangle with perimeter 8 to have the largest area, what dimensions should it have?
A)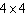
B)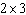
C)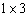
D)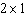
E)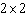
A)
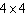
B)
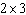
C)
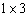
D)
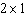
E)
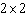

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
8
Maximize 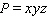 with
with 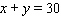 and
and 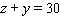 , and
, and 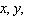 and
and 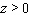 .
.
A)P = 4,000
B)P = 3,980
C)P = 12,000
D)P = 30
E)P = 3,990
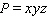 with
with 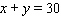 and
and 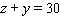 , and
, and 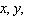 and
and 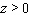 .
.A)P = 4,000
B)P = 3,980
C)P = 12,000
D)P = 30
E)P = 3,990

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
9
Find the exact location of all the absolute extrema of the function with domain 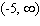 .
. 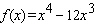
A)(9, -2187)- absolute minimum
B)(-9, -2187)- relative maximum
C)(9, -2187)- relative minimum
D)(9, 2187)- absolute minimum
E)(9, 0)- absolute maximum
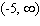 .
. 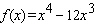
A)(9, -2187)- absolute minimum
B)(-9, -2187)- relative maximum
C)(9, -2187)- relative minimum
D)(9, 2187)- absolute minimum
E)(9, 0)- absolute maximum

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
10
The cost of controlling emissions at a firm goes up rapidly as the amount of emissions reduced goes up. Here is a possible model: 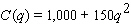 where q is the reduction in emissions (in pounds of pollutant per day)and C is the daily cost to the firm (in dollars)of this reduction. Government clean air subsidies amount to $750 per pound of pollutant removed. How many pounds of pollutant should the firm remove each day to minimize net cost (cost minus subsidy)?
where q is the reduction in emissions (in pounds of pollutant per day)and C is the daily cost to the firm (in dollars)of this reduction. Government clean air subsidies amount to $750 per pound of pollutant removed. How many pounds of pollutant should the firm remove each day to minimize net cost (cost minus subsidy)?
A)2.5 pounds
B)75 pounds
C)2 pounds
D)5 pounds
E)10 pounds
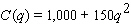 where q is the reduction in emissions (in pounds of pollutant per day)and C is the daily cost to the firm (in dollars)of this reduction. Government clean air subsidies amount to $750 per pound of pollutant removed. How many pounds of pollutant should the firm remove each day to minimize net cost (cost minus subsidy)?
where q is the reduction in emissions (in pounds of pollutant per day)and C is the daily cost to the firm (in dollars)of this reduction. Government clean air subsidies amount to $750 per pound of pollutant removed. How many pounds of pollutant should the firm remove each day to minimize net cost (cost minus subsidy)?A)2.5 pounds
B)75 pounds
C)2 pounds
D)5 pounds
E)10 pounds

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
11
Find the exact location of all the relative and absolute extrema of the function with domain 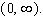
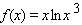
A)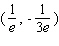 - relative minimum
- relative minimum
B)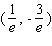 - relative maximum
- relative maximum
C)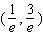 - absolute minimum
- absolute minimum
D)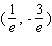 - absolute minimum
- absolute minimum
E)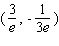 - absolute minimum
- absolute minimum
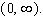
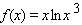
A)
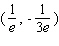 - relative minimum
- relative minimumB)
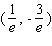 - relative maximum
- relative maximumC)
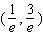 - absolute minimum
- absolute minimumD)
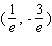 - absolute minimum
- absolute minimumE)
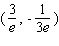 - absolute minimum
- absolute minimum
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
12
Find the exact location of all the relative and absolute extrema of the function. 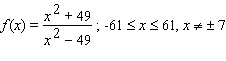
A)(0, -1)- absolute maximum
B)(0, -49)- absolute minimum
C)(0, 49)- absolute maximum
D)(0, -1)- relative minimum
E)(0, -1)- relative maximum
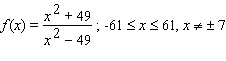
A)(0, -1)- absolute maximum
B)(0, -49)- absolute minimum
C)(0, 49)- absolute maximum
D)(0, -1)- relative minimum
E)(0, -1)- relative maximum

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
13
Find the exact location of all the relative and absolute extrema of the function with domain 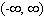 .
. 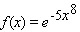
A)(1, 5)- absolute maximum
B)(0, 1)- absolute minimum
C)(1, 0)- absolute maximum
D)(0, 1)- absolute maximum
E)(0, 8)- relative minimum
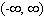 .
. 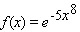
A)(1, 5)- absolute maximum
B)(0, 1)- absolute minimum
C)(1, 0)- absolute maximum
D)(0, 1)- absolute maximum
E)(0, 8)- relative minimum

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
14
Minimize 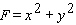 with
with 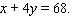
A)F = 68
B)F = 4
C)F = 272
D)F = 256
E)F = 204
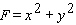 with
with 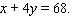
A)F = 68
B)F = 4
C)F = 272
D)F = 256
E)F = 204

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
15
Maximize 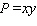 with
with 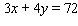 .
.
A)P = 4
B)P = 72
C)P = 1,200
D)P = 108
E)P = 216
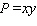 with
with 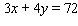 .
.A)P = 4
B)P = 72
C)P = 1,200
D)P = 108
E)P = 216

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
16
Find the exact location of all the relative and absolute extrema of the function with domain  .
. 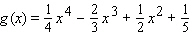
A)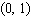 - relative maximum
- relative maximum
B)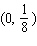 - absolute minimum
- absolute minimum
C)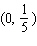 - absolute minimum
- absolute minimum
D)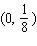 - absolute maximum
- absolute maximum
E)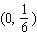 - relative maximum
- relative maximum
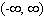 .
. 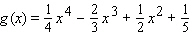
A)
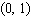 - relative maximum
- relative maximumB)
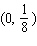 - absolute minimum
- absolute minimumC)
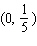 - absolute minimum
- absolute minimumD)
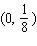 - absolute maximum
- absolute maximumE)
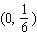 - relative maximum
- relative maximum
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
17
I want to fence in a rectangular vegetable patch. The fencing for the east and west sides costs $5 per foot, while the fencing for the north and south sides costs only $3 per foot. I have a budget of $150 for the project. What is the largest area I can enclose?
A)187.5 square feet
B)93.75 square feet
C)150 square feet
D)15 square feet
E)375 square feet
A)187.5 square feet
B)93.75 square feet
C)150 square feet
D)15 square feet
E)375 square feet

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
18
The graph of the derivative of a function f is shown. Determine the x -coordinates of all stationary and singular points of f . (Assume that f ( x )is defined and continuous everywhere in -10, 1 .) 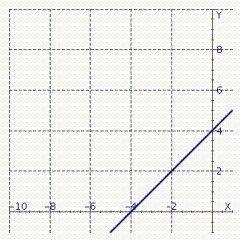
A)x = 3
B)x = -1
C)x = -3
D)x = -4
E)x = 9

A)x = 3
B)x = -1
C)x = -3
D)x = -4
E)x = 9

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
19
The fruit yield per tree in an orchard that contains 50 trees is 100 pounds per tree each year. Due to crowding, the yield decreases by 1 pounds per season per every additional tree planted. How many additional trees should be planted for a maximum total annual yield?
A)25 additional trees
B)50 additional trees
C)15 additional trees
D)75 additional trees
E)20 additional trees
A)25 additional trees
B)50 additional trees
C)15 additional trees
D)75 additional trees
E)20 additional trees

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
20
Your automobile assembly plant has a Cobb-Douglas production function given by 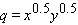 where q is the number of automobiles it produced per year, x is the number of employees, and y is the daily operating budget (in dollars). Annual operating costs amount to an average of $10,000 per employee plus the operating budget of $
where q is the number of automobiles it produced per year, x is the number of employees, and y is the daily operating budget (in dollars). Annual operating costs amount to an average of $10,000 per employee plus the operating budget of $ 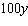 . Assume you wish to produce 1,000 automobiles per year at a minimum cost. How many employees should you hire?
. Assume you wish to produce 1,000 automobiles per year at a minimum cost. How many employees should you hire?
A)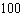 employees
employees
B)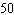 employees
employees
C)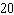 employees
employees
D)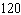 employees
employees
E)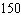 employees
employees
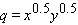 where q is the number of automobiles it produced per year, x is the number of employees, and y is the daily operating budget (in dollars). Annual operating costs amount to an average of $10,000 per employee plus the operating budget of $
where q is the number of automobiles it produced per year, x is the number of employees, and y is the daily operating budget (in dollars). Annual operating costs amount to an average of $10,000 per employee plus the operating budget of $ 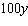 . Assume you wish to produce 1,000 automobiles per year at a minimum cost. How many employees should you hire?
. Assume you wish to produce 1,000 automobiles per year at a minimum cost. How many employees should you hire?A)
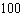 employees
employeesB)
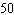 employees
employeesC)
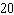 employees
employeesD)
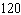 employees
employeesE)
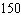 employees
employees
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
21
Calculate 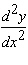 .
. 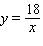
A)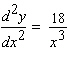
B)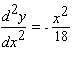
C)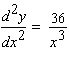
D)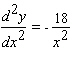
E)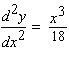
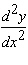 .
. 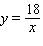
A)
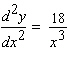
B)
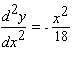
C)
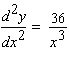
D)
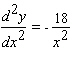
E)
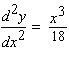

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
22
The position s of a point (in feet)is given as a function of time 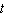 (in seconds).
(in seconds). 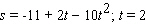 a. Find its acceleration as a function of
a. Find its acceleration as a function of 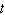 . b. Find its acceleration at the specified time.
. b. Find its acceleration at the specified time.
A)a ( t )= 20 ft/sec2, a ( t = 2)= 20 ft/sec2
B)a ( t )= -20 ft/sec2, a ( t = 2)= -20 ft/sec2
C)a ( t )= 24 ft/sec2, a ( t = 2)= -24 ft/sec2
D)a ( t )= -2 ft/sec2, a ( t = 2)= 2 ft/sec2
E)a ( t )= 5 ft/sec2, a ( t = 2)= 5 ft/sec2
 (in seconds).
(in seconds).  a. Find its acceleration as a function of
a. Find its acceleration as a function of 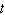 . b. Find its acceleration at the specified time.
. b. Find its acceleration at the specified time.A)a ( t )= 20 ft/sec2, a ( t = 2)= 20 ft/sec2
B)a ( t )= -20 ft/sec2, a ( t = 2)= -20 ft/sec2
C)a ( t )= 24 ft/sec2, a ( t = 2)= -24 ft/sec2
D)a ( t )= -2 ft/sec2, a ( t = 2)= 2 ft/sec2
E)a ( t )= 5 ft/sec2, a ( t = 2)= 5 ft/sec2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
23
The demand for rubies at Royal Ruby Retailers is given by 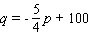 where p is the price RRR charges (in dollars)and q is the number of rubies RRR sells per week. At what price should RRR sell its rubies to maximize its weekly revenue? Please enter your answer in dollars without the units.
where p is the price RRR charges (in dollars)and q is the number of rubies RRR sells per week. At what price should RRR sell its rubies to maximize its weekly revenue? Please enter your answer in dollars without the units.
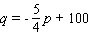 where p is the price RRR charges (in dollars)and q is the number of rubies RRR sells per week. At what price should RRR sell its rubies to maximize its weekly revenue? Please enter your answer in dollars without the units.
where p is the price RRR charges (in dollars)and q is the number of rubies RRR sells per week. At what price should RRR sell its rubies to maximize its weekly revenue? Please enter your answer in dollars without the units.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
24
Maximize 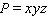 with
with 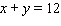 and
and 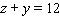 , and x , y , and
, and x , y , and 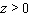 .
.
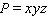 with
with 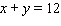 and
and 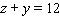 , and x , y , and
, and x , y , and 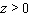 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
25
The Chocolate Box Co. is going to make open-topped boxes out of 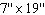 rectangles of cardboard by cutting squares out of the corners and folding up the sides. What is the largest volume box it can make this way?
rectangles of cardboard by cutting squares out of the corners and folding up the sides. What is the largest volume box it can make this way?
A)144 cubic inches
B)120 cubic inches
C)48 cubic inches
D)96 cubic inches
E)72 cubic inches
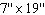 rectangles of cardboard by cutting squares out of the corners and folding up the sides. What is the largest volume box it can make this way?
rectangles of cardboard by cutting squares out of the corners and folding up the sides. What is the largest volume box it can make this way?A)144 cubic inches
B)120 cubic inches
C)48 cubic inches
D)96 cubic inches
E)72 cubic inches

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
26
Calculate 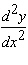 .
. 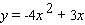
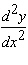 .
. 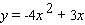

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
27
The position s of a point (in feet)is given as a function of time t (in seconds). 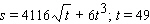 a. Find its acceleration as a function of
a. Find its acceleration as a function of 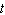 . b. Find its acceleration at the specified time.
. b. Find its acceleration at the specified time.
A)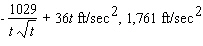
B)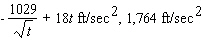
C)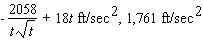
D)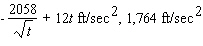
E)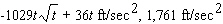
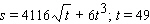 a. Find its acceleration as a function of
a. Find its acceleration as a function of 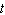 . b. Find its acceleration at the specified time.
. b. Find its acceleration at the specified time.A)
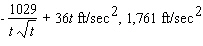
B)
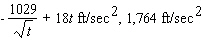
C)
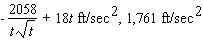
D)
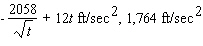
E)
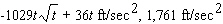

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
28
The FeatureRich Software Company sells its graphing program, Dogwood, with a volume discount. If a customer buys x copies, then that customer pays 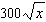 . It costs the company
. It costs the company 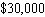 to develop the program and
to develop the program and 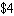 to manufacture each copy. If just one customer were to buy all the copies of Dogwood, how many copies would the customer have to buy for FeatureRich Software s average profit per copy to be maximized?
to manufacture each copy. If just one customer were to buy all the copies of Dogwood, how many copies would the customer have to buy for FeatureRich Software s average profit per copy to be maximized?
A)8,000 copies
B)20,000 copies
C)44,000 copies
D)40,000 copies
E)10,000 copies
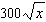 . It costs the company
. It costs the company 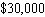 to develop the program and
to develop the program and 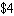 to manufacture each copy. If just one customer were to buy all the copies of Dogwood, how many copies would the customer have to buy for FeatureRich Software s average profit per copy to be maximized?
to manufacture each copy. If just one customer were to buy all the copies of Dogwood, how many copies would the customer have to buy for FeatureRich Software s average profit per copy to be maximized?A)8,000 copies
B)20,000 copies
C)44,000 copies
D)40,000 copies
E)10,000 copies

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
29
Fair Weather Airlines will accept only bags for which the sum of the length and width is 39 inches, while the sum of length, height, and twice the width is 78 inches. What is the largest volume of the bag that it will accept?
A)6,591 cubic inches
B)10,985 cubic inches
C)8,788 cubic inches
D)2,197 cubic inches
E)4,394 cubic inches
A)6,591 cubic inches
B)10,985 cubic inches
C)8,788 cubic inches
D)2,197 cubic inches
E)4,394 cubic inches

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
30
A company finds that the number of new products it develops per year depends on the size if its annual R D budget, x (in thousands of dollars), according to the following formula. 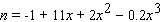 Find
Find 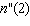 .
.
A)6.6
B)4.6
C)2.6
D)-2.4
E)1.6
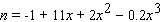 Find
Find 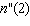 .
.A)6.6
B)4.6
C)2.6
D)-2.4
E)1.6

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
31
The graph of the second derivative, f ( x ), is given. 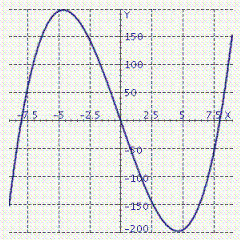 Determine the x -coordinates of all points of inflection of f ( x ), if any. (Assume that f ( x )is defined and continuous everywhere in
Determine the x -coordinates of all points of inflection of f ( x ), if any. (Assume that f ( x )is defined and continuous everywhere in 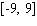 .)
.)
A)x = -5.6, x = 5.6
B)x = 8, x = 0, x = -8
C)x = -4.6, x = 0, x = 4.6
D)x = 0
E)x = -4.6, x = 4.6
 Determine the x -coordinates of all points of inflection of f ( x ), if any. (Assume that f ( x )is defined and continuous everywhere in
Determine the x -coordinates of all points of inflection of f ( x ), if any. (Assume that f ( x )is defined and continuous everywhere in 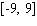 .)
.)A)x = -5.6, x = 5.6
B)x = 8, x = 0, x = -8
C)x = -4.6, x = 0, x = 4.6
D)x = 0
E)x = -4.6, x = 4.6

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
32
The graph of a function 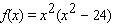 is given.
is given. 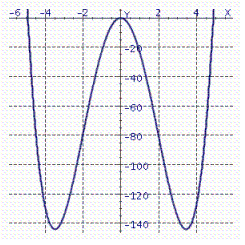 Find the coordinates of all points of inflection of this function (if any).
Find the coordinates of all points of inflection of this function (if any).
A)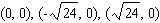
B)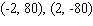
C)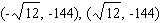
D)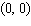
E)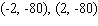
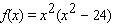 is given.
is given.  Find the coordinates of all points of inflection of this function (if any).
Find the coordinates of all points of inflection of this function (if any).A)
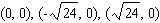
B)
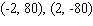
C)
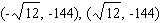
D)
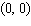
E)
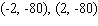

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
33
In 1965 the economist F.M. Scherer modeled the number, n , of patens produced by a firm as a function of the size, s , of the firm (measured in annual sales in millions of dollars). He came up with the following equation based on a study of 448 large firms. 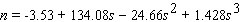 Find
Find 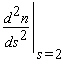 .
.
A)17.14
B)-32.18
C)-35.18
D)-27.18
E)-30.18
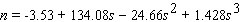 Find
Find 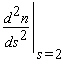 .
.A)17.14
B)-32.18
C)-35.18
D)-27.18
E)-30.18

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
34
Calculate 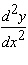 .
. 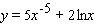
A)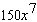
B)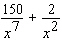
C)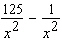
D)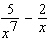
E)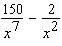
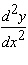 .
. 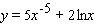
A)
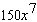
B)
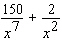
C)
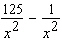
D)
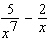
E)
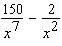

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
35
You manage a small antique store that owns a collection of Louis XVI jewelry boxes. Their value v is increasing according to the formula 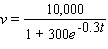 where t is the number of years from now. You anticipate an inflation rate of 2% per year, so that the present value of an item that will be worth $ v in t years time is given by
where t is the number of years from now. You anticipate an inflation rate of 2% per year, so that the present value of an item that will be worth $ v in t years time is given by 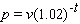 In how many years from now will the greatest rate of increase of the present value of your antiques be attained?
In how many years from now will the greatest rate of increase of the present value of your antiques be attained?
A)t = 17.58 years
B)t = 60.60 years
C)t = 5.45 years
D)t = 18.18 years
E)t = 2.73 years
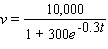 where t is the number of years from now. You anticipate an inflation rate of 2% per year, so that the present value of an item that will be worth $ v in t years time is given by
where t is the number of years from now. You anticipate an inflation rate of 2% per year, so that the present value of an item that will be worth $ v in t years time is given by 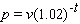 In how many years from now will the greatest rate of increase of the present value of your antiques be attained?
In how many years from now will the greatest rate of increase of the present value of your antiques be attained?A)t = 17.58 years
B)t = 60.60 years
C)t = 5.45 years
D)t = 18.18 years
E)t = 2.73 years

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
36
Calculate 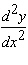 .
. 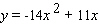
A)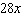
B)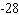
C)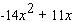
D)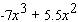
E)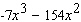
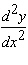 .
. 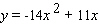
A)
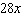
B)
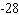
C)
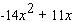
D)
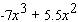
E)
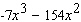

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
37
A packaging company is going to make closed boxes, with square bases, that hold 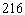 cubic centimeters. What are the dimensions of the box that can be built with the least material?
cubic centimeters. What are the dimensions of the box that can be built with the least material?
A)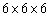 cm
cm
B)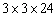 cm
cm
C)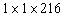 cm
cm
D)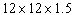 cm
cm
E)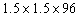 cm
cm
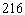 cubic centimeters. What are the dimensions of the box that can be built with the least material?
cubic centimeters. What are the dimensions of the box that can be built with the least material?A)
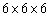 cm
cmB)
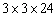 cm
cmC)
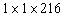 cm
cmD)
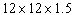 cm
cmE)
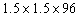 cm
cm
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
38
Calculate 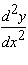 .
. 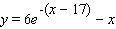
A)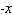
B)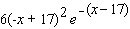
C)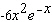
D)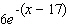
E)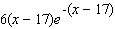
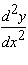 .
. 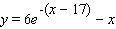
A)
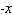
B)
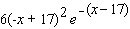
C)
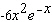
D)
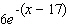
E)
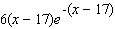

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
39
Calculate 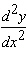 .
. 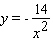
A)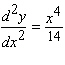
B)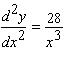
C)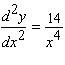
D)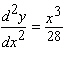
E)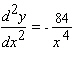
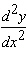 .
. 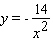
A)
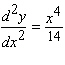
B)
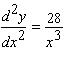
C)
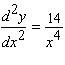
D)
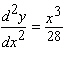
E)
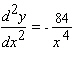

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
40
The position s of a point (in feet)is given as a function of time 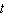 (in seconds).
(in seconds). 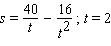 a. Find its acceleration as a function of
a. Find its acceleration as a function of 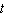 . b. Find its acceleration at the specified time.
. b. Find its acceleration at the specified time.
A)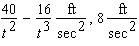
B)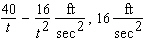
C)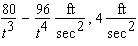
D)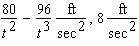
E)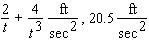
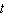 (in seconds).
(in seconds). 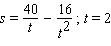 a. Find its acceleration as a function of
a. Find its acceleration as a function of 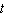 . b. Find its acceleration at the specified time.
. b. Find its acceleration at the specified time.A)
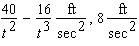
B)
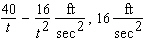
C)
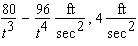
D)
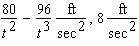
E)
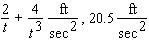

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
41
A baseball diamond is a square with side 90 ft. A batter at the home base hits the ball and runs toward first base with a speed of 26 ft/sec. At what rate is his distance from third base increasing when he is halfway to first base? 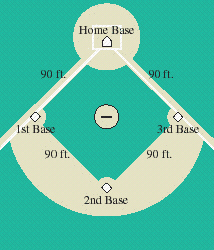
A)8.7 ft/sec
B)11.6 ft/sec
C)58.1 ft/sec
D)13.0 ft/sec
E)18.4 ft/sec

A)8.7 ft/sec
B)11.6 ft/sec
C)58.1 ft/sec
D)13.0 ft/sec
E)18.4 ft/sec

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
42
My aunt and I were approaching the same intersection, she from the south and I from the west. She was travelling at a steady speed of 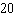 mph, while I was approaching the intersection at
mph, while I was approaching the intersection at 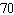 mph. At a certain instant in time, I was
mph. At a certain instant in time, I was 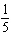 of a mile from the intersection, while she was
of a mile from the intersection, while she was 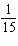 of a mile from it. How fast were we approaching each other at that instant?
of a mile from it. How fast were we approaching each other at that instant?
A)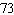 miles per hour
miles per hour
B)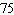 miles per hour
miles per hour
C)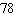 miles per hour
miles per hour
D) miles per hour
miles per hour
E) miles per hour
miles per hour
 mph, while I was approaching the intersection at
mph, while I was approaching the intersection at  mph. At a certain instant in time, I was
mph. At a certain instant in time, I was 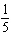 of a mile from the intersection, while she was
of a mile from the intersection, while she was 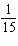 of a mile from it. How fast were we approaching each other at that instant?
of a mile from it. How fast were we approaching each other at that instant?A)
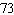 miles per hour
miles per hourB)
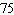 miles per hour
miles per hourC)
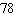 miles per hour
miles per hourD)
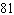 miles per hour
miles per hourE)
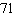 miles per hour
miles per hour
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
43
The population P is currently 30,000 and growing at a rate of 6,000 per year. What is the mathematical notation for the rate?
A)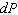
B)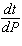
C)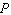
D)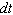
E)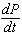
A)
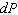
B)
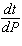
C)
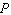
D)
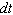
E)
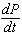

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
44
A rather flimsy spherical balloon is designed to pop at the instant its radius has reached 5 cm. Assuming the balloon is filled with helium at a rate of 5 cm 3 /s, calculate how fast the diameter is growing at the instant it pops. The volume of a sphere of radius r is 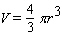 .
.
A)0.016 cm/s
B)0.127 cm/s
C)0.212 cm/s
D)0.159 cm/s
E)0.032 cm/s
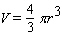 .
.A)0.016 cm/s
B)0.127 cm/s
C)0.212 cm/s
D)0.159 cm/s
E)0.032 cm/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
45
A spherical party balloon is being inflated by helium pumped in at a rate 3 cubic feet per minute. How fast is the radius growing at the instant when the radius has reached 1 foot? The volume of a sphere of radius r is 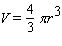 .
.
A)0.64 feet per minute
B)0.72 feet per minute
C)0.76 feet per minute
D)0.14 feet per minute
E)0.24 feet per minute
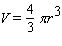 .
.A)0.64 feet per minute
B)0.72 feet per minute
C)0.76 feet per minute
D)0.14 feet per minute
E)0.24 feet per minute

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
46
There are presently N = 200 cases of Bangkok flu, and the number is growing by 50 new cases every month. Rewrite the rate in mathematical notation.
A)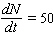
B)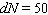
C)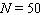
D)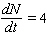
E)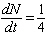
A)
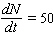
B)
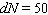
C)
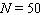
D)
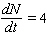
E)
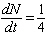

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
47
Find the coordinates of all relative and absolute extrema. 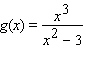
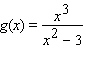

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
48
Combined SAT scores in the United States could be approximated by 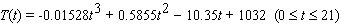 in the years 1965 - 1986. Here t is the number of years since 1965, and T is the combined SAT score average for the United States. Find all points of inflection of the graph of T , and interpret the result. Enter your answers rounded to the nearest hundredth.
in the years 1965 - 1986. Here t is the number of years since 1965, and T is the combined SAT score average for the United States. Find all points of inflection of the graph of T , and interpret the result. Enter your answers rounded to the nearest hundredth.
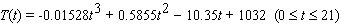 in the years 1965 - 1986. Here t is the number of years since 1965, and T is the combined SAT score average for the United States. Find all points of inflection of the graph of T , and interpret the result. Enter your answers rounded to the nearest hundredth.
in the years 1965 - 1986. Here t is the number of years since 1965, and T is the combined SAT score average for the United States. Find all points of inflection of the graph of T , and interpret the result. Enter your answers rounded to the nearest hundredth.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
49
Demand for your tie-dyed T-shirts is given by the formula 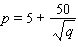 where p is the price in dollars you can charge to sell q T-shirts per month. If you currently sell T-shirts for $10 each and you raise price by $2 each month, how fast will the demand drop?
where p is the price in dollars you can charge to sell q T-shirts per month. If you currently sell T-shirts for $10 each and you raise price by $2 each month, how fast will the demand drop?
A)80 T-shirts per month
B)20,000 T-shirts per month
C)400 T-shirts per month
D)10 T-shirts per month
E)40 T-shirts per month
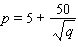 where p is the price in dollars you can charge to sell q T-shirts per month. If you currently sell T-shirts for $10 each and you raise price by $2 each month, how fast will the demand drop?
where p is the price in dollars you can charge to sell q T-shirts per month. If you currently sell T-shirts for $10 each and you raise price by $2 each month, how fast will the demand drop?A)80 T-shirts per month
B)20,000 T-shirts per month
C)400 T-shirts per month
D)10 T-shirts per month
E)40 T-shirts per month

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
50
The base of a 25-foot ladder is being pulled away from a wall at a rate of 12 feet per second. How fast is the top of the ladder sliding down the wall at the instance when the base of the ladder is 15 feet from the wall?
A)36 ft/s
B)3 ft/s
C)48 ft/s
D)16 ft/s
E)9 ft/s
A)36 ft/s
B)3 ft/s
C)48 ft/s
D)16 ft/s
E)9 ft/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
51
Find the coordinates of all relative and absolute extrema. 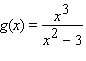
A)(-3, -4.5), (3, 4.5), (0, 0)
B)(0, 0), (3, 4.5)
C)(-3, -4.5), (3, 4.5)
D)(-1, 1), (0, 0)
E)(0, 0)
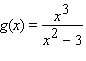
A)(-3, -4.5), (3, 4.5), (0, 0)
B)(0, 0), (3, 4.5)
C)(-3, -4.5), (3, 4.5)
D)(-1, 1), (0, 0)
E)(0, 0)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
52
Sketch the graph of the function, labeling all relative and absolute extrema and points of inflection, and vertical and horizontal asymptotes. Check your graph using technology. 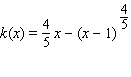
A)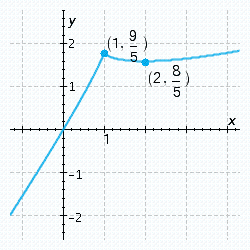
B)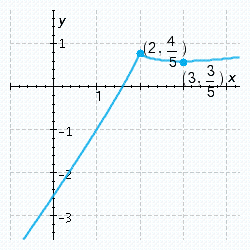
C)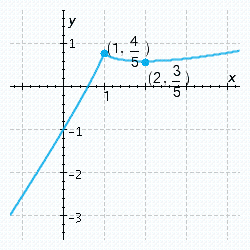
D)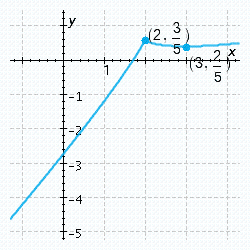
E)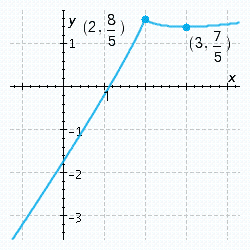
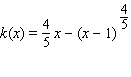
A)

B)
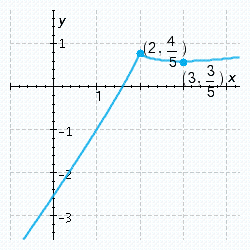
C)

D)

E)
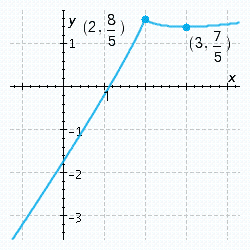

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
53
You can now sell 200 cups of lemonade at 60 cents per cup, but demand is dropping at a rate of 10 cups per week each week. Assuming that raising the price doesn't affect the demand, how fast do you have to raise your price if you want to keep the revenue constant?
A)3 cents per week
B)6 cents per week
C)5 cents per week
D)2 cents per week
E)7 cents per week
A)3 cents per week
B)6 cents per week
C)5 cents per week
D)2 cents per week
E)7 cents per week

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
54
The HMS Dreadnaught is 40 miles north of Montauk and steaming due north at 20 mph, while the USS Mona Lisa is 50 miles east of Montauk and steaming due east at an even 30 mph. How fast is their distance apart increasing?
A)88 miles per hour
B)33 miles per hour
C)41 miles per hour
D)36 miles per hour
E)72 miles per hour
A)88 miles per hour
B)33 miles per hour
C)41 miles per hour
D)36 miles per hour
E)72 miles per hour

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
55
The area of a circular sun spot is growing at a rate of 1,200 km 2/s. How fast is the radius growing at the instant when it equals 10,000 km?
A)8.333 km/s
B)0.000 km/s
C)0.038 km/s
D)0.019 km/s
E)0.060 km/s
A)8.333 km/s
B)0.000 km/s
C)0.038 km/s
D)0.019 km/s
E)0.060 km/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
56
Assume that the demand function for tuna in a small coastal town is given by 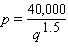 where q is the number of pounds of tuna that can be sold in 1 month at the price of p dollars per pound. The town s fishery finds that the demand for tuna is currently 900 pounds per month and is increasing at a rate of 50 pounds per month. How fast is the price changing?
where q is the number of pounds of tuna that can be sold in 1 month at the price of p dollars per pound. The town s fishery finds that the demand for tuna is currently 900 pounds per month and is increasing at a rate of 50 pounds per month. How fast is the price changing?
A)$0.123 per pound per month
B)$1.111 per pound per month
C)$0.082 per pound per month
D)$0.055 per pound per month
E)$0.041 per pound per month
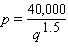 where q is the number of pounds of tuna that can be sold in 1 month at the price of p dollars per pound. The town s fishery finds that the demand for tuna is currently 900 pounds per month and is increasing at a rate of 50 pounds per month. How fast is the price changing?
where q is the number of pounds of tuna that can be sold in 1 month at the price of p dollars per pound. The town s fishery finds that the demand for tuna is currently 900 pounds per month and is increasing at a rate of 50 pounds per month. How fast is the price changing?A)$0.123 per pound per month
B)$1.111 per pound per month
C)$0.082 per pound per month
D)$0.055 per pound per month
E)$0.041 per pound per month

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
57
The radius of a circular puddle is growing at a rate of 2 cm/s. How fast is the area growing at the instant when it equals 20 cm 2?
A)32 cm 2/s
B)10 cm 2/s
C)251 cm 2/s
D)16 cm 2/s
E)18 cm 2/s
A)32 cm 2/s
B)10 cm 2/s
C)251 cm 2/s
D)16 cm 2/s
E)18 cm 2/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
58
Combined SAT scores in the United States could be approximated by 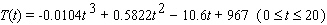 in the years 1968 - 1988. Here t is the number of years since 1968, and T is the combined SAT score average for the United States. Find all points of inflection of the graph of T , and interpret the result.
in the years 1968 - 1988. Here t is the number of years since 1968, and T is the combined SAT score average for the United States. Find all points of inflection of the graph of T , and interpret the result.
A)(20, 904.12)
B)(18.71, 903.81)
C)(0, 0)
D)(15.85, 903.33), (21.58, 904.30)
E)(0, 0), (20, 904.12)
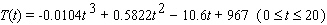 in the years 1968 - 1988. Here t is the number of years since 1968, and T is the combined SAT score average for the United States. Find all points of inflection of the graph of T , and interpret the result.
in the years 1968 - 1988. Here t is the number of years since 1968, and T is the combined SAT score average for the United States. Find all points of inflection of the graph of T , and interpret the result.A)(20, 904.12)
B)(18.71, 903.81)
C)(0, 0)
D)(15.85, 903.33), (21.58, 904.30)
E)(0, 0), (20, 904.12)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
59
The graph of a function 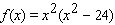 is given.
is given. 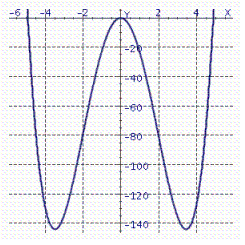 Find the coordinates of all points of inflection of this function (if any). Please enter your answer as ordered pairs in the form ( x , y )separated by commas.
Find the coordinates of all points of inflection of this function (if any). Please enter your answer as ordered pairs in the form ( x , y )separated by commas.
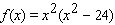 is given.
is given.  Find the coordinates of all points of inflection of this function (if any). Please enter your answer as ordered pairs in the form ( x , y )separated by commas.
Find the coordinates of all points of inflection of this function (if any). Please enter your answer as ordered pairs in the form ( x , y )separated by commas.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
60
The automobile assembly plant you manage has a Cobb-Douglas production function given by 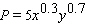 where P is the number of automobiles the plant produces per year, x is the number of employees, and y is the daily operating budget (in dollars). You maintain a production level of 5,000 automobiles per year. If you currently employ 150 workers and are hiring new workers at a rate of 10 per year, how fast is your daily operating budget changing?
where P is the number of automobiles the plant produces per year, x is the number of employees, and y is the daily operating budget (in dollars). You maintain a production level of 5,000 automobiles per year. If you currently employ 150 workers and are hiring new workers at a rate of 10 per year, how fast is your daily operating budget changing?
A)-$9,663.33 per year
B)$45.10 per year
C)$64.42 per year
D)$350.74 per year
E)-$64.42 per year
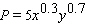 where P is the number of automobiles the plant produces per year, x is the number of employees, and y is the daily operating budget (in dollars). You maintain a production level of 5,000 automobiles per year. If you currently employ 150 workers and are hiring new workers at a rate of 10 per year, how fast is your daily operating budget changing?
where P is the number of automobiles the plant produces per year, x is the number of employees, and y is the daily operating budget (in dollars). You maintain a production level of 5,000 automobiles per year. If you currently employ 150 workers and are hiring new workers at a rate of 10 per year, how fast is your daily operating budget changing?A)-$9,663.33 per year
B)$45.10 per year
C)$64.42 per year
D)$350.74 per year
E)-$64.42 per year

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
61
The consumer demand curve for tissues is given by 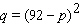 where p is the price per case of tissues and q is the demand in weekly sales. Determine the elasticity of demand E when the price is set at $30. Round the answer to the nearest hundredth.
where p is the price per case of tissues and q is the demand in weekly sales. Determine the elasticity of demand E when the price is set at $30. Round the answer to the nearest hundredth.
A)0.65
B)0.97
C)0.48
D)0.01
E)1.94
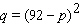 where p is the price per case of tissues and q is the demand in weekly sales. Determine the elasticity of demand E when the price is set at $30. Round the answer to the nearest hundredth.
where p is the price per case of tissues and q is the demand in weekly sales. Determine the elasticity of demand E when the price is set at $30. Round the answer to the nearest hundredth.A)0.65
B)0.97
C)0.48
D)0.01
E)1.94

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
62
The weekly sales in Honolulu Red Oranges is given by the following equation. 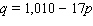 Calculate the elasticity of demand for a price of $23 per orange.
Calculate the elasticity of demand for a price of $23 per orange.
A)-0.63
B)-0.09
C)0.63
D)1.35
E)-1.35
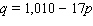 Calculate the elasticity of demand for a price of $23 per orange.
Calculate the elasticity of demand for a price of $23 per orange.A)-0.63
B)-0.09
C)0.63
D)1.35
E)-1.35

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
63
A general hyperbolic demand function has the form to follow. 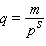 (
( 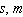 - nonzero constants)Obtain a formula for the elasticity of demand at a unit price of
- nonzero constants)Obtain a formula for the elasticity of demand at a unit price of 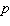 .
.
A)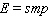
B)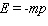
C)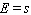
D)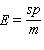
E)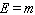
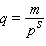 (
( 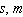 - nonzero constants)Obtain a formula for the elasticity of demand at a unit price of
- nonzero constants)Obtain a formula for the elasticity of demand at a unit price of 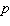 .
.A)
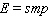
B)
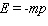
C)
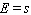
D)
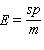
E)
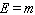

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
64
The consumer demand curve for tissues is given by 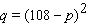 where p is the price per case of tissues and q is the demand in weekly sales. At what price should tissues be sold to maximize the revenue?
where p is the price per case of tissues and q is the demand in weekly sales. At what price should tissues be sold to maximize the revenue?
A)$54.00
B)$108.00
C)$72.00
D)$36.00
E)$32.00
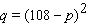 where p is the price per case of tissues and q is the demand in weekly sales. At what price should tissues be sold to maximize the revenue?
where p is the price per case of tissues and q is the demand in weekly sales. At what price should tissues be sold to maximize the revenue?A)$54.00
B)$108.00
C)$72.00
D)$36.00
E)$32.00

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
65
A right conical circular vessel is being filled with green industrial waste at a rate of 150 cubic meters per second. How fast is the level rising after 150  cubic meters have been poured in? (The cone has height 75 m and radius 45 m at its brim. The volume of a cone of height h and cross-sectional radius r at its brim is given by
cubic meters have been poured in? (The cone has height 75 m and radius 45 m at its brim. The volume of a cone of height h and cross-sectional radius r at its brim is given by 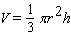 .)
.)
A)3.4 m/s
B)0.2 m/s
C)1.1 m/s
D)0.7 m/s
E)3.6 m/s
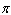 cubic meters have been poured in? (The cone has height 75 m and radius 45 m at its brim. The volume of a cone of height h and cross-sectional radius r at its brim is given by
cubic meters have been poured in? (The cone has height 75 m and radius 45 m at its brim. The volume of a cone of height h and cross-sectional radius r at its brim is given by 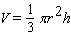 .)
.)A)3.4 m/s
B)0.2 m/s
C)1.1 m/s
D)0.7 m/s
E)3.6 m/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
66
A point on the graph of 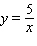 is moving along the curve in such a way that its x -coordinate is increasing at a rate of 2 units per second. At what rate is the y -coordinate decreasing at the instant the y -coordinate is equal to 10?
is moving along the curve in such a way that its x -coordinate is increasing at a rate of 2 units per second. At what rate is the y -coordinate decreasing at the instant the y -coordinate is equal to 10?
A)40 units per second
B)20 units per second
C)5 units per second
D)4 units per second
E)50 units per second
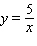 is moving along the curve in such a way that its x -coordinate is increasing at a rate of 2 units per second. At what rate is the y -coordinate decreasing at the instant the y -coordinate is equal to 10?
is moving along the curve in such a way that its x -coordinate is increasing at a rate of 2 units per second. At what rate is the y -coordinate decreasing at the instant the y -coordinate is equal to 10?A)40 units per second
B)20 units per second
C)5 units per second
D)4 units per second
E)50 units per second

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
67
A fried chicken franchise finds that the demand equation for its new roast chicken product, Roasted Rooster , is given by 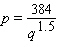 where p is the price (in dollars)per quarter-chicken serving and q is the number of quarter-chicken servings that can be sold per hour at this price. Express q as a function of p , and find the elasticity of demand when the price is set at $6 per serving.
where p is the price (in dollars)per quarter-chicken serving and q is the number of quarter-chicken servings that can be sold per hour at this price. Express q as a function of p , and find the elasticity of demand when the price is set at $6 per serving.
A)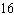
B)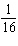
C)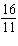
D)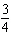
E)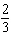
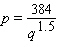 where p is the price (in dollars)per quarter-chicken serving and q is the number of quarter-chicken servings that can be sold per hour at this price. Express q as a function of p , and find the elasticity of demand when the price is set at $6 per serving.
where p is the price (in dollars)per quarter-chicken serving and q is the number of quarter-chicken servings that can be sold per hour at this price. Express q as a function of p , and find the elasticity of demand when the price is set at $6 per serving.A)
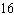
B)
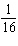
C)
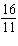
D)
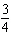
E)
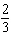

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
68
A general exponential demand function has the form to follow. 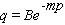 ( B , m - nonzero constants)Obtain a formula for the elasticity of demand at a unit price of p .
( B , m - nonzero constants)Obtain a formula for the elasticity of demand at a unit price of p .
A)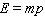
B)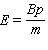
C)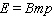
D)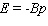
E)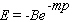
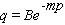 ( B , m - nonzero constants)Obtain a formula for the elasticity of demand at a unit price of p .
( B , m - nonzero constants)Obtain a formula for the elasticity of demand at a unit price of p .A)
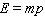
B)
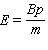
C)
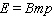
D)
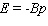
E)
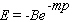

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
69
A general quadratic demand function has the form to follow. 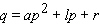 ( a , l , r are constants,
( a , l , r are constants, 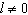 )Obtain a formula for the elasticity of demand at a unit price p .
)Obtain a formula for the elasticity of demand at a unit price p .
A)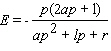
B)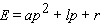
C)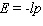
D)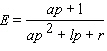
E)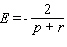
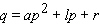 ( a , l , r are constants,
( a , l , r are constants, 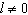 )Obtain a formula for the elasticity of demand at a unit price p .
)Obtain a formula for the elasticity of demand at a unit price p .A)
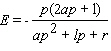
B)
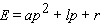
C)
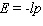
D)
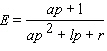
E)
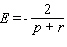

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
70
A cylindrical bucket is being filled with paint at a rate of 4 cm 3/min. How fast is the level rising when the bucket starts to overflow? The bucket has a height of 50 cm and a radius of 10 cm.
A)0.013 cm/min
B)0.315 cm/min
C)0.164 cm/min
D)0.617 cm/min
E)0.768 cm/min
A)0.013 cm/min
B)0.315 cm/min
C)0.164 cm/min
D)0.617 cm/min
E)0.768 cm/min

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
71
The volume of paint in a right cylindrical can is given by 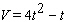 , where
, where 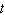 is time in seconds and
is time in seconds and 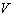 is the volume in cm 3 . How fast is the level rising when the height is 4 cm? The can has a height of 6 cm and a radius of 1 cm. Hint: To get
is the volume in cm 3 . How fast is the level rising when the height is 4 cm? The can has a height of 6 cm and a radius of 1 cm. Hint: To get 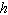 as a function of
as a function of 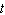 , first solve the volume
, first solve the volume 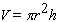 for
for 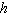 .
.
A)7 cm/s
B)5 cm/s
C)8 cm/s
D)10 cm/s
E)6 cm/s
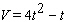 , where
, where 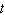 is time in seconds and
is time in seconds and 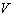 is the volume in cm 3 . How fast is the level rising when the height is 4 cm? The can has a height of 6 cm and a radius of 1 cm. Hint: To get
is the volume in cm 3 . How fast is the level rising when the height is 4 cm? The can has a height of 6 cm and a radius of 1 cm. Hint: To get 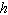 as a function of
as a function of 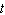 , first solve the volume
, first solve the volume 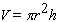 for
for 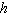 .
.A)7 cm/s
B)5 cm/s
C)8 cm/s
D)10 cm/s
E)6 cm/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
72
A point is moving along the circle 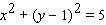 in such a way that its x -coordinate is decreasing at a rate of 3 units per second. At what rate is the y -coordinate decreasing at the instant when the point has reached ( 2, 2)?
in such a way that its x -coordinate is decreasing at a rate of 3 units per second. At what rate is the y -coordinate decreasing at the instant when the point has reached ( 2, 2)?
A)8 units per second
B)6 units per second
C)10 units per second
D)7 units per second
E)5.5 units per second
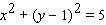 in such a way that its x -coordinate is decreasing at a rate of 3 units per second. At what rate is the y -coordinate decreasing at the instant when the point has reached ( 2, 2)?
in such a way that its x -coordinate is decreasing at a rate of 3 units per second. At what rate is the y -coordinate decreasing at the instant when the point has reached ( 2, 2)?A)8 units per second
B)6 units per second
C)10 units per second
D)7 units per second
E)5.5 units per second

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
73
A general linear demand function has the form to follow. 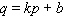 (
( 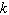 and
and 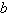 constants, with
constants, with 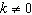 )Obtain a formula for the elasticity of the demand at a unit price
)Obtain a formula for the elasticity of the demand at a unit price 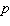 .
.
A)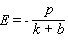
B)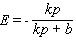
C)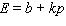
D)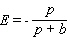
E)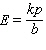
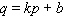 (
( 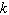 and
and 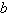 constants, with
constants, with 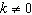 )Obtain a formula for the elasticity of the demand at a unit price
)Obtain a formula for the elasticity of the demand at a unit price 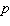 .
.A)
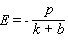
B)
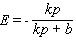
C)
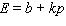
D)
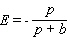
E)
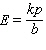

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
74
The estimated monthly sales of Mona Lisa paint-by-number sets is given by the formula 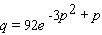 where
where 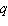 is the demand in monthly sales and
is the demand in monthly sales and 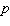 is the retail price in yen. Determine the elasticity of demand
is the retail price in yen. Determine the elasticity of demand 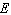 when the retail price is set at 5 yen.
when the retail price is set at 5 yen.
A)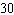
B)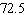
C)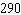
D)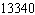
E)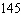
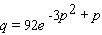 where
where 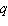 is the demand in monthly sales and
is the demand in monthly sales and 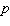 is the retail price in yen. Determine the elasticity of demand
is the retail price in yen. Determine the elasticity of demand 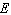 when the retail price is set at 5 yen.
when the retail price is set at 5 yen.A)
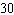
B)
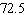
C)
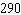
D)
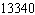
E)
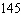

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
75
A study of about 1800 U.S. colleges and universities resulted in the demand equation 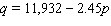 where q is the enrollment at a college or university and p is the average annual tuition (plus fees)it charges. The study also found that the average tuition charged by universities and colleges was $2,127. What is the corresponding elasticity of demand?
where q is the enrollment at a college or university and p is the average annual tuition (plus fees)it charges. The study also found that the average tuition charged by universities and colleges was $2,127. What is the corresponding elasticity of demand?
A)1.55
B)0.30
C)1.16
D)-0.78
E)0.78
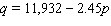 where q is the enrollment at a college or university and p is the average annual tuition (plus fees)it charges. The study also found that the average tuition charged by universities and colleges was $2,127. What is the corresponding elasticity of demand?
where q is the enrollment at a college or university and p is the average annual tuition (plus fees)it charges. The study also found that the average tuition charged by universities and colleges was $2,127. What is the corresponding elasticity of demand?A)1.55
B)0.30
C)1.16
D)-0.78
E)0.78

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
76
The estimated monthly sales of Mona Lisa paint-by-number sets is given by the formula 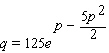 where
where 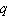 is the demand in monthly sales and
is the demand in monthly sales and 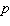 is the retail price in yen. At what price will revenue be a maximum? Round the answer to the nearest hundredth.
is the retail price in yen. At what price will revenue be a maximum? Round the answer to the nearest hundredth.
A)1.22 yen
B)0.78 yen
C)0.99 yen
D)0.56 yen
E)69.78 yen
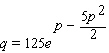 where
where 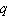 is the demand in monthly sales and
is the demand in monthly sales and 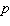 is the retail price in yen. At what price will revenue be a maximum? Round the answer to the nearest hundredth.
is the retail price in yen. At what price will revenue be a maximum? Round the answer to the nearest hundredth.A)1.22 yen
B)0.78 yen
C)0.99 yen
D)0.56 yen
E)69.78 yen

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
77
The weekly sales in Honolulu Red Oranges is given by the following. 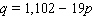 Calculate the price that gives a maximum weekly revenue.
Calculate the price that gives a maximum weekly revenue.
A)$14.50
B)$30.00
C)$58.00
D)$31.00
E)$29.00
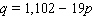 Calculate the price that gives a maximum weekly revenue.
Calculate the price that gives a maximum weekly revenue.A)$14.50
B)$30.00
C)$58.00
D)$31.00
E)$29.00

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
78
The consumer demand curve for Professor Stefan Schwartzenegger dumbbells is given by 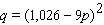 where p is the price per dumbbell and q is the demand in weekly sales. Find the price Professor Schwartzenegger should charge for his dumbbells in order to maximize revenue.
where p is the price per dumbbell and q is the demand in weekly sales. Find the price Professor Schwartzenegger should charge for his dumbbells in order to maximize revenue.
A)$342
B)$38
C)$40
D)$34
E)$29
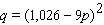 where p is the price per dumbbell and q is the demand in weekly sales. Find the price Professor Schwartzenegger should charge for his dumbbells in order to maximize revenue.
where p is the price per dumbbell and q is the demand in weekly sales. Find the price Professor Schwartzenegger should charge for his dumbbells in order to maximize revenue.A)$342
B)$38
C)$40
D)$34
E)$29

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
79
A general linear demand function has the form that follows. 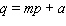 (
( 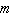 and
and 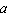 constants, with
constants, with 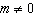 )Obtain a formula for the price that maximizes revenue.
)Obtain a formula for the price that maximizes revenue.
A)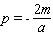
B)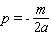
C)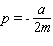
D)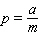
E)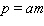
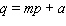 (
( 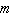 and
and 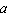 constants, with
constants, with 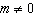 )Obtain a formula for the price that maximizes revenue.
)Obtain a formula for the price that maximizes revenue.A)
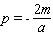
B)
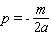
C)
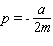
D)
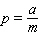
E)
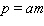

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
80
A study found that the divorce rate d (given as a percentage)appears to depend on the ratio r of available men to available women. This function can be approximated by 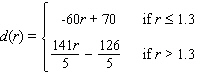 There are currently 0.8 available men per available woman in Littleville, and this ratio is increasing by 0.15 per year. At what percent is the divorce rate decreasing?
There are currently 0.8 available men per available woman in Littleville, and this ratio is increasing by 0.15 per year. At what percent is the divorce rate decreasing?
A)0.12% per year
B)21.15% per year
C)0.75% per year
D)10.5% per year
E)9% per year
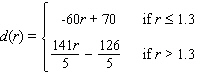 There are currently 0.8 available men per available woman in Littleville, and this ratio is increasing by 0.15 per year. At what percent is the divorce rate decreasing?
There are currently 0.8 available men per available woman in Littleville, and this ratio is increasing by 0.15 per year. At what percent is the divorce rate decreasing?A)0.12% per year
B)21.15% per year
C)0.75% per year
D)10.5% per year
E)9% per year

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck


