Deck 19: Logistic Regression
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/30
Play
Full screen (f)
Deck 19: Logistic Regression
1
In which of the following situations can binary logistic regression be used?
A) Kate wants to examine if gender (0=male, 1=female) can predict the aggression level of teenagers. She uses the number of self-reported aggressive behaviors in the previous month as the measure of aggression level.
B) Amy wants to use aggression level to predict whether a student will finish high school (0=no, 1=yes). The aggression level is measured by the occurrence of self-reported aggressive behaviors in the previous month.
C) Pete wants to predict the starting salary of teachers based on their highest level of education (Associate, Bachelor, Master, Ph. D or professional).
D) Mike wants to use parents' level of education to predict the highest level of education achieved by their children. He codes the level of education into six categories: some school, high school graduate, some college, two-year college, four-year college, and postgraduate.
A) Kate wants to examine if gender (0=male, 1=female) can predict the aggression level of teenagers. She uses the number of self-reported aggressive behaviors in the previous month as the measure of aggression level.
B) Amy wants to use aggression level to predict whether a student will finish high school (0=no, 1=yes). The aggression level is measured by the occurrence of self-reported aggressive behaviors in the previous month.
C) Pete wants to predict the starting salary of teachers based on their highest level of education (Associate, Bachelor, Master, Ph. D or professional).
D) Mike wants to use parents' level of education to predict the highest level of education achieved by their children. He codes the level of education into six categories: some school, high school graduate, some college, two-year college, four-year college, and postgraduate.
B
2
Which one of the following can be used as an appropriate independent variable for binary logistic regression?
A) dichotomous variable
B) multinomial variable
C) continuous variable
D) none of the above
E) all of the above
A) dichotomous variable
B) multinomial variable
C) continuous variable
D) none of the above
E) all of the above
E
3
Which one of the following statements is true about OLS regression and logistic regression?
A) OLS regression uses continuous variables as independent variables, whereas logistic regression uses categorical variables as independent variables.
B) OLS regression assumes that the conditional distribution of the dependent variable is normal, whereas logistic regression makes no such assumption.
C) In OLS regression the predicted value (Y') is continuous, whereas in logistic regression the predicted probability is either 0 or 1.
D) In OLS regression there are always residuals in the model, whereas in logistic regression there are no residuals or errors.
A) OLS regression uses continuous variables as independent variables, whereas logistic regression uses categorical variables as independent variables.
B) OLS regression assumes that the conditional distribution of the dependent variable is normal, whereas logistic regression makes no such assumption.
C) In OLS regression the predicted value (Y') is continuous, whereas in logistic regression the predicted probability is either 0 or 1.
D) In OLS regression there are always residuals in the model, whereas in logistic regression there are no residuals or errors.
B
4
Which of the following would be appropriate outcomes to examine with binary logistic regression?
A) Types of college degree (associate's degree, bachelor's degree)
B) Levels of education (high school, college, postgraduate)
C) Marital status (single, common-law married, married, divorced, separated, widowed)
D) Grades in a test (A, B, C, D, E)
E) All of the above
A) Types of college degree (associate's degree, bachelor's degree)
B) Levels of education (high school, college, postgraduate)
C) Marital status (single, common-law married, married, divorced, separated, widowed)
D) Grades in a test (A, B, C, D, E)
E) All of the above

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
5
Based on a logistic regression model, the odds of Sandy passing a test is 4. Based on the odds, what is the probability that Sandy will pass the test?
A) 0.8
B) 0.4
C) 0.25
D) 0.2
E) cannot be determined.
A) 0.8
B) 0.4
C) 0.25
D) 0.2
E) cannot be determined.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
6
Based on a logistic regression model, Cindy did some calculation and predicted that the probability of her passing a test is 0.5. What are the odds that Sue will pass the test?
A) 1/2
B) 1
C) 2
D) 5
E) cannot be determined.
A) 1/2
B) 1
C) 2
D) 5
E) cannot be determined.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following statements about the relationship between Odds(Y=1) and Logit(Y) is false?
A) When the odds increase, the logit of Y increases.
B) When the odds are larger than 1, the logit of Y has positive value.
C) When the odds are smaller than 1, the logit of Y has negative value.
D) When the odds are 1, the logit of Y may either be positive or negative.
A) When the odds increase, the logit of Y increases.
B) When the odds are larger than 1, the logit of Y has positive value.
C) When the odds are smaller than 1, the logit of Y has negative value.
D) When the odds are 1, the logit of Y may either be positive or negative.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
8
In the logistic regression model, which of the following is assumed to have a linear relationship with the independent variables?
A) the dichotomous variable Y
B) Odds(Y =1)
C) logit(Y), i.e., the log odds ratio
D) error term
A) the dichotomous variable Y
B) Odds(Y =1)
C) logit(Y), i.e., the log odds ratio
D) error term

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
9
A study was conducted to investigate variables associated with dropping out of high school. The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1= dropped out of high school; 0= did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-What is being predicted in this model?
A) The mean difference in cumulative GPA between students who dropped out of high school and those who finished high school.
B) The percentage of students who will drop out before graduating high school.
C) The odds that a student will drop out of high school.
D) The odds that a student had been retained in at least one grade if he dropped out of high school.
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1= dropped out of high school; 0= did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-What is being predicted in this model?
A) The mean difference in cumulative GPA between students who dropped out of high school and those who finished high school.
B) The percentage of students who will drop out before graduating high school.
C) The odds that a student will drop out of high school.
D) The odds that a student had been retained in at least one grade if he dropped out of high school.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
10
A study was conducted to investigate variables associated with dropping out of high school. The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1= dropped out of high school; 0= did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-Based on logistic regression, if a student has been retained in at least one grade, the chance that he/she will drop out of high school
A) increases.
B) decreases.
C) stays the same.
D) is uncertain.
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1= dropped out of high school; 0= did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-Based on logistic regression, if a student has been retained in at least one grade, the chance that he/she will drop out of high school
A) increases.
B) decreases.
C) stays the same.
D) is uncertain.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
11
A study was conducted to investigate variables associated with dropping out of high school. The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1= dropped out of high school; 0= did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-If Mindy has a high school GPA of 3, and has never repeated a grade, which of the following predictions can be derived from the model?
A) Mindy has more than 50% probability of dropping out of high school.
B) Mindy has less than 50% probability of dropping out of high school.
C) Mindy has exactly 50% probability of dropping out of high school.
D) Mindy will drop out of high school.
E) Mindy will not drop out of high school.
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1= dropped out of high school; 0= did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-If Mindy has a high school GPA of 3, and has never repeated a grade, which of the following predictions can be derived from the model?
A) Mindy has more than 50% probability of dropping out of high school.
B) Mindy has less than 50% probability of dropping out of high school.
C) Mindy has exactly 50% probability of dropping out of high school.
D) Mindy will drop out of high school.
E) Mindy will not drop out of high school.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
12
In logistic regression, which of the following statements about probability, odds, and log odds is true?
A) Probability, odds, and log odds can all be computed from the regression line.
B) Probability, odds, and log odds all have the same range of possible values.
C) Probability, odds, and log odds are all assumed to have a linear relationship with the independent variables.
D) Probability, odds, and log odds are all measured on the same scale.
A) Probability, odds, and log odds can all be computed from the regression line.
B) Probability, odds, and log odds all have the same range of possible values.
C) Probability, odds, and log odds are all assumed to have a linear relationship with the independent variables.
D) Probability, odds, and log odds are all measured on the same scale.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
13
Aaron is studying smoking behavior and has coded "smoker" as "1" and "non-smoker" as "0." Which of the following is a correct interpretation if the odds ratio is equal to 1?
A) The probability of being a smoker is equal to that of being a non-smoker.
B) The probability of being a smoker is substantially greater than that of being a non-smoker.
C) The probability of being a smoker is substantially smaller than that of being a non-smoker.
D) Cannot be determined from the information provided.
A) The probability of being a smoker is equal to that of being a non-smoker.
B) The probability of being a smoker is substantially greater than that of being a non-smoker.
C) The probability of being a smoker is substantially smaller than that of being a non-smoker.
D) Cannot be determined from the information provided.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
14
For a logistic regression model, if −2LL = 0, it indicates that
A) the model has perfect fit but the model cannot be estimated.
B) the model is a poor fit to the data.
C) the value of the log likelihood function is 0.
D) a computational error has been made.
A) the model has perfect fit but the model cannot be estimated.
B) the model is a poor fit to the data.
C) the value of the log likelihood function is 0.
D) a computational error has been made.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
15
Herbert is studying the risk factors associated with heart diseases. He identified three risk factors (age, sex, and cholesterol level), and built two different models.
Model 1: Logit(Yi) = -7 + 2.5X1 - X2. -2LL = 3
Model 2: Logit(Yi) = -8.5 + 1.5X3 -2LL = 8
Y: 1= diagnosed with major heart disease; 0 = no major heart disease;
X1: age in years (above 40);
X2: sex, where 0 is male and 1 is female;
X3: cholesterol level (in mmol/L)
Herbert conducted a log likelihood difference test (p = .025) and concluded that Model 1 fit the data significantly better than Model 2. Evaluate his analysis.
A) The analysis is not valid. The two models cannot be compared using the log likelihood difference test because they are not nested models.
B) The interpretation of the test results is erroneous. The fact that the null hypothesis is rejected indicates that Model 2 fit the data better than Model 1.
C) The interpretation of the test results is erroneous. The fact that null hypothesis is rejected indicates that Model 1 and Model 2 do not differ substantially in fit.
D) There is nothing wrong with the analysis.
Model 1: Logit(Yi) = -7 + 2.5X1 - X2. -2LL = 3
Model 2: Logit(Yi) = -8.5 + 1.5X3 -2LL = 8
Y: 1= diagnosed with major heart disease; 0 = no major heart disease;
X1: age in years (above 40);
X2: sex, where 0 is male and 1 is female;
X3: cholesterol level (in mmol/L)
Herbert conducted a log likelihood difference test (p = .025) and concluded that Model 1 fit the data significantly better than Model 2. Evaluate his analysis.
A) The analysis is not valid. The two models cannot be compared using the log likelihood difference test because they are not nested models.
B) The interpretation of the test results is erroneous. The fact that the null hypothesis is rejected indicates that Model 2 fit the data better than Model 1.
C) The interpretation of the test results is erroneous. The fact that null hypothesis is rejected indicates that Model 1 and Model 2 do not differ substantially in fit.
D) There is nothing wrong with the analysis.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
16
If the logistic regression model is a good fit to the data, which of the following test(s) will likely have significant results?
A) log likelihood difference test
B) Hosmer-Lemeshow goodness-of-fit test
C) both a and b
D) neither a nor b
A) log likelihood difference test
B) Hosmer-Lemeshow goodness-of-fit test
C) both a and b
D) neither a nor b

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
17
In logistic regression, the multiple R2 pseudovariance explained values
A) measure the proportion of variance explained in the dichotomous outcome variable.
B) measure the effect size for the model.
C) will increase as more variables are added to the model.
D) are generally small for models with good fit.
A) measure the proportion of variance explained in the dichotomous outcome variable.
B) measure the effect size for the model.
C) will increase as more variables are added to the model.
D) are generally small for models with good fit.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
18
Aaron is studying smoking behavior and has coded "smoker" as "1" and "non-smoker" as "0." The predictor is the number of family members who smoke. Which of the following is a correct interpretation of an odds ratio of +2?
A) For every additional family member who smokes, the odds of being a smoker increase by 100%.
B) For every additional family member who smokes, the odds of being a smoker decrease by 100%.
C) For every one-unit increase in being a smoker, the odds of having a family member who smoke increase by 100%.
D) For every one-unit increase in being a smoker, the odds of having a family member who smoke decrease by 100%.
A) For every additional family member who smokes, the odds of being a smoker increase by 100%.
B) For every additional family member who smokes, the odds of being a smoker decrease by 100%.
C) For every one-unit increase in being a smoker, the odds of having a family member who smoke increase by 100%.
D) For every one-unit increase in being a smoker, the odds of having a family member who smoke decrease by 100%.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
19
In the smoking study, Aaron has obtained the following classification table. 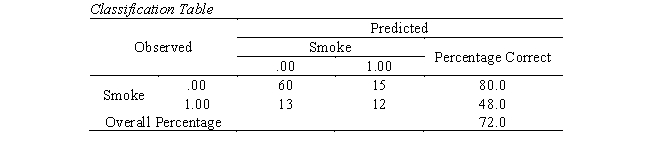
-What is the false positive rate?
A) 20%
B) 28%
C) 48%
D) 52%

-What is the false positive rate?
A) 20%
B) 28%
C) 48%
D) 52%

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
20
In the smoking study, Aaron has obtained the following classification table. 
-What is the false negative rate?
A) 20%
B) 28%
C) 48%
D) 52%

-What is the false negative rate?
A) 20%
B) 28%
C) 48%
D) 52%

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
21
In the smoking study, Aaron has obtained the following classification table. 
-If a person is predicted to be a smoker, we would expect that
A) the person has a good chance of actually being a smoker, because the model has an adequate overall predictive accuracy.
B) the person has a good chance of actually being a smoker, because the model has high specificity.
C) the person may or may not be a smoker, because the model has low sensitivity.
D) the person may or may not be a smoker, because the false positive rate is high.

-If a person is predicted to be a smoker, we would expect that
A) the person has a good chance of actually being a smoker, because the model has an adequate overall predictive accuracy.
B) the person has a good chance of actually being a smoker, because the model has high specificity.
C) the person may or may not be a smoker, because the model has low sensitivity.
D) the person may or may not be a smoker, because the false positive rate is high.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
22
In the likelihood ratio test of the overall regression model, if the null hypothesis, H0: 1 = 2 =... = m = 0, is rejected, it means that
A) the baseline model fits the data well.
B) the baseline model has better fit than the regression model.
C) the baseline model fits the data as well as the regression model.
D) the regression model has better fit than the baseline model.
A) the baseline model fits the data well.
B) the baseline model has better fit than the regression model.
C) the baseline model fits the data as well as the regression model.
D) the regression model has better fit than the baseline model.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
23
Which of the following is NOT a statistic that can be used to evaluate individual regression coefficients for logistic regression models?
A) Cox and Snell R squared
B) 2 in the change in log likelihood test
C) Wald statistic
D) BIC
A) Cox and Snell R squared
B) 2 in the change in log likelihood test
C) Wald statistic
D) BIC

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
24
A logistic regression model is estimated to be logit(Yi) = -40 + 5X1, where X1 is a continuous variable. Which assumption does not need to be examined?
A) noncollineary
B) independence
C) linearity
D) All of the above assumptions need to be examined.
A) noncollineary
B) independence
C) linearity
D) All of the above assumptions need to be examined.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
25
In logistic regression, the assumption of linearity does not need to be examined in which of the following situations?
A) When the dependent variable is categorical.
B) When all the independent variables are categorical.
C) When all the independent variables are continuous.
D) When some of the independent variables are categorical, and some of them are continuous.
E) The assumption of linearity always needs to be examined.
A) When the dependent variable is categorical.
B) When all the independent variables are categorical.
C) When all the independent variables are continuous.
D) When some of the independent variables are categorical, and some of them are continuous.
E) The assumption of linearity always needs to be examined.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
26
Complete the missing information for this table (Y is a dichotomous variable).
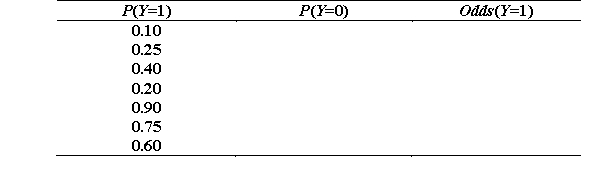


Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
27
You are given the following data, where X1 (high school cumulative GPA) and X2 (having repeated grade; 0 = never repeated any grade and 1 = have repeated at least one grade; use 0 as the reference category) are used to predict Y (dropping out of high school, "1," vs. graduating high school, "0"). ( = .05)
Determine the following values based on simultaneous entry of the independent variables: ?2LL, constant, b1, b2, se(b1), se(b2), odds ratios, Wald1, Wald2.
Determine the following values based on simultaneous entry of the independent variables: ?2LL, constant, b1, b2, se(b1), se(b2), odds ratios, Wald1, Wald2.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
28
Complete the missing information for Table 1, using 0.50 as the cut value. Then complete the classification table (Table 2). Compute sensitivity, specificity, false positive rate, and false negative rate.
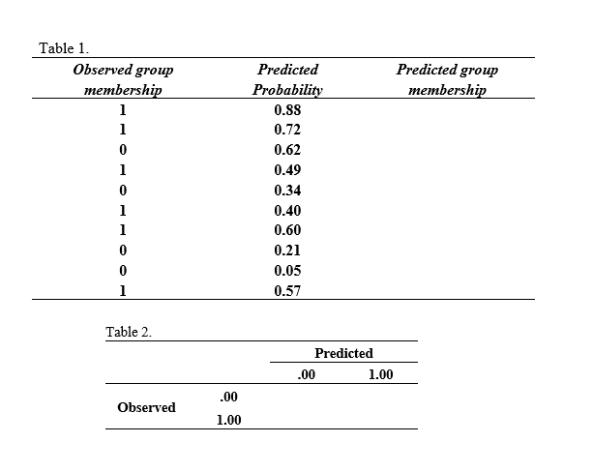


Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
29
You are given the following data, where X1 (sex; male = 0, female =1; use 0 as the reference category) and X2 (having at least one immediate family member who smokes; yes = 1, no = 0; use 0 as the reference category) are used to predict Y (being a smoker = 1 vs. being a nonsmoker = 0). ( = .05)
Determine the following values based on simultaneous entry of independent variables: ?2LL, constant, b1, b2, se(b1), se(b2), odds ratios, Wald1, Wald2.
Determine the following values based on simultaneous entry of independent variables: ?2LL, constant, b1, b2, se(b1), se(b2), odds ratios, Wald1, Wald2.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
30
Professor Pruefung wanted to examine if performance in quizzes can predict whether a student will pass or fail the final exam. The independent variables are scores in two pop quizzes (Quiz1, Quiz2), and the dependent variable is a dichotomous variable (pass = 1 vs. fail = 0). Below is part of the output of the analysis.
(a) Professor Pruefung assumed that the better a student performed in the quizzes (a higher score indicates better performance), the higher the odds that he/she will pass the final exam. If that is the case, what are the expected signs for b1 and b2? Do the results confirm the expectation?
(b) Based on the tables, is there any indication of assumptions violation? If so, which assumption(s) has (have) been violated?
(c) What are the possible consequences of the assumption violation?
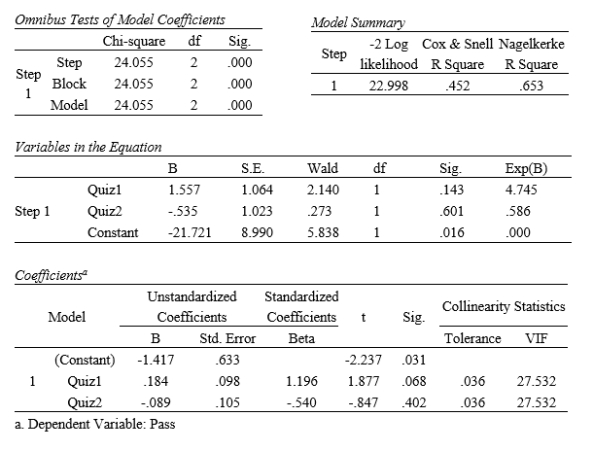
(a) Professor Pruefung assumed that the better a student performed in the quizzes (a higher score indicates better performance), the higher the odds that he/she will pass the final exam. If that is the case, what are the expected signs for b1 and b2? Do the results confirm the expectation?
(b) Based on the tables, is there any indication of assumptions violation? If so, which assumption(s) has (have) been violated?
(c) What are the possible consequences of the assumption violation?


Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck


