Deck 15: Random- and Mixed-Effects Analysis of Variance Models

Question 1

The denominator of the F ratio used to test the main effect of factor A in a two-factor ANOVA is MS_AB in which one of the following?

A) Fixed-effects model
B) Mixed-effects model where A is the fixed factor
C) Mixed-effects model where A is the random factor
D) Split-plot model where A is the between-subjects factor
E) Split-plot model where A is the within-subjects factor

Answer 1

B

Question 2

Candace conducts a study to examine the effect of a professional development program on teachers' content knowledge. Half of the teachers are randomly assigned to participate in the program (the other half are controls). All teachers are then tested on their content knowledge each month over the course of the academic year. Which ANOVA model is most appropriate for analysis of these data?

A) One-factor random-effects model
B) Two-factor random-effects model
C) Two-factor mixed-effects model
D) One-factor repeated measures design
E) Two-factor split-plot design

Answer 2

E

Question 3

Gilbert wants to make generalizations about the class attendance rate in his district. He randomly samples four schools and collects data on the attendance rate of 50 classes (one class represents one observation). Which ANOVA model is most appropriate for analysis of these data?

A) One-factor random-effects model
B) Two-factor random-effects model
C) Two-factor mixed-effects model
D) One-factor repeated measures design
E) Two-factor split-plot design

Answer 3

A

Question 4

In the same study as described in Question 3, Gilbert randomly selected 25 classes from the four sampled schools. All selected classes participated in a program that aimed to increase attendance rate (the remaining classes were controls). Gilbert then collected data on the change of attendance rate to see whether the program made a difference. Which ANOVA model is most appropriate for analysis of these data?

A) One-factor random-effects model
B) Two-factor random-effects model
C) Two-factor mixed-effects model
D) One-factor repeated measures design
E) Two-factor split-plot design

Question 5

Ravi conducts a study where randomly selected patients of a clinic are measured on their blood pressure each month over the course of one year. Which ANOVA model is most appropriate for analysis of these data?

A) One-factor random-effects model
B) Two-factor random-effects model
C) Two-factor mixed-effects model
D) One-factor repeated measures design
E) Two-factor split-plot design

Question 6

In the same study as described in Question 5, suppose Ravi randomly assigned half of the selected patients to follow a specific diet plan (the other half are controls). Patient blood pressure is recorded every month over the course of one year. Ravi wanted to examine whether the diet plan made any difference in blood pressure. Which ANOVA model is most appropriate for analysis of these data?

A) One-factor random-effects model
B) Two-factor random-effects model
C) Two-factor mixed-effects model
D) One-factor repeated measures design
E) Two-factor split-plot design

Question 7

In a taste test, the participants are asked to taste each of the three types of pies (the order is counterbalanced), and then rate how much they like each flavor. To compare the average ratings for each type of pie, which ANOVA model is most appropriate?

A) One-factor random-effects model
B) Two-factor random-effects model
C) Two-factor mixed-effects model
D) One-factor repeated measures design
E) Two-factor split-plot design

Question 8

If a given set of data were analyzed with both a two-factor fixed-effects model and a two-factor random-effects model, which F ratio will definitely stay unchanged?

A) F_A
B) F_B
C) F_AB
D) All of the above
E) None of the above

Question 9

Suppose two researchers perform a one-factor ANOVA on the same data, but researcher A assumes a fixed-effects model, whereas researcher B assumes a random-effects model. Which of the following statements is false?

A) Two researchers will have the same null hypothesis.
B) Two researchers will obtain the same F ratio.
C) Two researchers will obtain the same p value.
D) Two researchers will obtain the same critical F value if they use the same significance level.

Question 10

Which of the following statements regarding a comparison of the fixed- effects and random-effects models is false?

A) One can make generalization about all levels of the factor with random- effects models, but not with fixed-effects models.
B) One can exactly replicate studies using fixed-effects models, but studies using random-effects models cannot be exactly replicated.
C) One can conduct MCP with fixed-effects models, but not with random- effects models.
D) Both fixed-effects model and random-effects models can be used in a repeated design.

Question 11

When testing the interaction effect of a two-factor design, which of the following models does not use MS_with as the denominator for that F ratio?

A) Two-factor fixed-effects model
B) Two-factor random-effects model
C) Two-factor mixed-effects model
D) Two-factor split-plot design
E) All models use MS_with as the denominator for F_AB

Question 12

How many hypotheses are tested in a one-factor repeated measures ANOVA?

A) 1
B) 2
C) 3
D) 4
E) It depends.

Question 13

How many hypotheses are tested in a two-factor split-plot ANOVA?

A) 1
B) 2
C) 3
D) 4
E) It depends.

Question 14

In a two-factor mixed-effects ANOVA, A (fixed factor) has 3 levels, and B (random factor) has 5 levels. Each cell has 5 observations. What is df_with?

A) 15
B) 60
C) 74
D) 75

Question 15

In a two-factor ANOVA, A (fixed factor) has 3 levels, and B (random factor) has 5 levels. Each cell has 5 observations. The F_A ratio has degrees of freedom equal to?

A) 2, 8
B) 2, 15
C) 2, 60
D) 2, 74
E) None of the above.

Question 16

In a one-factor repeated measures ANOVA, A (fixed factor) has 4 levels, and each cell has 10 observations. The F_A ratio has degrees of freedom equal to?

A) 4, 9
B) 4,27
C) 3,27
D) 3,36

Question 17

In a two-factor split-plot ANOVA, A (between-subjects factor) has 3 levels, B (within-subjects factor) has 4 levels, and each cell has 5 observations. The F_A ratio has degrees of freedom equal to?

A) 2, 4
B) 2, 6
C) 2, 12
D) 2, 36

Question 18

In the table below, each cell represents one combination of factor levels. The actual experiment assigns participants only to the combinations represented by the shaded cells (the rows are randomly selected). This experiment is an example of which of the following designs?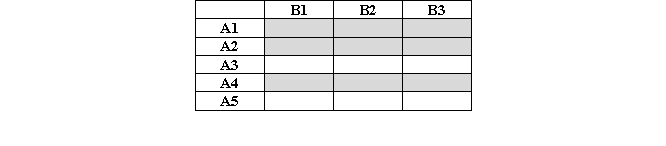

A) A two-factor fixed-effects design.
B) A two-factor random-effects design.
C) A two-factor mixed-effects design, where A is the fixed factor.
D) A two-factor mixed-effects design, where B is the fixed factor.
E) A nested design.

Question 19

In a one-factor random-effects model, suppose we find that the effect of factor A is significant at $\alpha$ = .05.

A) We should conduct MCP on
B) We should conduct MCP only when A has more than two levels.
C) We conclude that not all the $\mu$ _.j. are equal at significance level .05.
D) We are sure that the effect of A will also be significant if we have applied a fixed-effects model to the data.

Question 20

MCP can be used to further examine

A) the significant interaction effect in a two-factor random-effect model.
B) the significant interaction effect in a two-factor mixed-effect model.
C) the significant main effect of a between-subjects fixed factor in a two-factor split plot model.
D) the significant main effect of a within-subjects random factor in a two- factor split plot model.

Question 21

In two-factor mixed-effects ANOVA (A is the fixed-effects factor and B is the random-effects factor), which of the following statements is not always true?

A) E(MS_A) ≥ E(MS_AB)
B) E(MS_B) ≥ E(MS_AB)
C) E(MS_A) ≥ E(MS_with)
D) E(MS_B) ≥ E(MS_with)
E) E(MS_AB) ≥ E(MS_with)

Question 22

In which of the following models can the population variance of the residual errors ( $\sigma$ _{$\varepsilon$} ²) be estimated?

A) Two-factor fixed-effects model.
B) One-factor repeated measures design.
C) Two-factor split-plot design.
D) All of the above.

Question 23

Which model(s) generally requires the assumption of sphericity?

A) One-factor repeated design.
B) Two-factor split plot design.
C) Three-factor design with two between-subjects factors and one within- subjects factor.
D) All of the above.
E) None of the above.

Question 24

In one-factor repeated measures model, scores are collected at three different time points (J = 3). The assumption of sphericity basically states that

A) The variance of scores collected at each time point is the same.
B) The variance of the difference scores between the first time point and the second time point is the same as that between the second time point and the third time point.
C) The variance of the difference scores is the same for each of the three pairs of time points.
D) Both the variance and covariance of the difference scores are the same for each of the three pairs of time points.

Question 25

If the assumption of sphericity (i.e., compound symmetry) is violated, what should the researcher do?

A) Because the effects of assumption violation will be minimal, we should use the results of the usual F test anyway.
B) If H₀ is rejected using the usual F test, we should use alternative F tests to verify the results.
C) If H₀ is not rejected using the usual F test, we should use alternative F tests to verify the results.
D) Because the usual F test is not valid, we cannot analyze the data using this ANOVA model.

Question 26

Complete the following ANOVA summary table for a two-factor model, where there are two levels of factor A (fixed program effect) and five levels of factor B (random school effect). Each cell of the design includes seven students ( $\alpha$ = .05).
$\begin{array}{ccccccc}\hline \text { Source } & S S & d f & M S & F & \text { Critical Value } & \text { Decision } \\\hline \mathrm{A} & 100 & - & - & - & - & - \\\mathrm{B} & 210 & - & - & - & - & - \\\mathrm{AB} & - & - & 20 & - & - & - \\\text { Within } & -& - & - & & & \\\text { Total } & 690 & & & & \\\hline\end{array}$

Question 27

Complete the following ANOVA summary table for a two-factor model, where there are three levels of factor A (random dosage effect) and four levels of factor B (random physician effect). Each cell of the design includes six patients ( $\alpha$ = .05).
$\begin{array}{ccccccc}\hline \text { Source } & S S & d f & M S & F & \text { Critical Value } & \text { Decision } \\\hline \mathrm{A} & 25 & - & - & - & - & - \\\mathrm{B} & - & - & 15 & - & - & - \\\mathrm{AB} & - & - & - & - & - & - \\\text { Within } & - & - & 1 & & & \\\text { Total } & {160} & - & & & & \\\hline\end{array}$

Question 28

To examine development in the pedagogical content knowledge (PCK) of new teachers, 12 novice teachers are measured on their PCK at the beginning of their teaching career, at the end of the first semester, and at the end of the first school year. The scale that measures PCK ranges from 0 to 45 with higher scores reflecting greater levels of PCK. The data are shown below. Conduct a one-factor repeated measures ANOVA to determine the mean differences across time, using $\alpha$ = .05. Use the Bonferroni method to detect exactly where the differences are among the time points (if they are different).
$\begin{array}{|c|c|c|c|}\hline \text { Subject } & \text { Time 1 } & \text { Time 2 } & \text { Time 3 } \\\hline 1 & 16 & 17 & 28 \\\hline 2 & 17 & 23 & 32 \\\hline 3 & 11 & 21 & 30 \\\hline 4 & 15 & 23 & 35 \\\hline 5 & 21 & 32 & 40 \\\hline 6 & 14 & 22 & 31 \\\hline 7 & 12 & 19 & 31 \\\hline 8 & 17 & 21 & 25 \\\hline 9 & 11 & 16 & 24 \\\hline 10 & 8 & 14 & 20 \\\hline 11 & 14 & 24 & 28 \\\hline 12 & 12 & 19 & 25 \\\hline\end{array}$

Question 29

Using the same data as in Problem 3, conduct a two-factor split-plot ANOVA, where the first six teachers participate in a professional development program throughout their first year of teaching, and the last six teachers do not participate in the program ( $\alpha$ = 05). Does the program seem to have an effect on the change in teachers' pedagogical content knowledge?

Question 30

Dr. Bellus wants to study how people's perception of attractiveness is affected by the gender of the subjects, and the facial expression of the object. Each participant views six headshots (in random order) of the same person, who demonstrates different facial expressions (joy, surprise, fear, anger, sadness, and disgust) in each picture. The participants are then asked to rate the attractiveness level of each picture. The rating is the dependent variable. Below is the selected output of a two-factor split plot ANOVA.
Test of Between-Subjects Effects
$\begin{array}{ccccc}\hline \text { Source } & \text { Type III SS } & \text { df } & \text { MS } & \text { F } \\\hline \text { A (between-subjects factor) } & 226.81 & 1 & 226.81 & 3.04 \\\text { S (subject) } & 2084.61 & 28 & 74.45 & \\\hline\end{array}$ Test of Within-Subjects Effects
$\begin{array}{l}\text { Test of Within-Subjects Effects }\\\begin{array}{ccccc}\hline \text { Source } & \text { Type III SS } & \text { df } & \text { MS } & \text { F } \\\hline \text { B (within-subjects factor) } & 18802.53 & 5 & 3760.506 & 38.07 \\\mathrm{~A}^{*} \mathrm{~B} & 324.22 & 5 & 64.84 & 0.66 \\\mathrm{~B}^{*} \mathrm{~S} & 13829.70 & 140 & 98.78 & \\\hline\end{array}\end{array}$
(a) Identify the between-subjects factor and within-subjects factor.
(b) Are the effects significant ( $\alpha$ = .05)? What do these results tell us about people's perception of attractiveness?
(c) Is MCP necessary? If so, which effect(s) should we conduct MCP on?