Deck 11: Repeated-Measures Analysis of Variance
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/3
Play
Full screen (f)
Deck 11: Repeated-Measures Analysis of Variance
What kind of question would be best examined with a repeated-measures ANOVA?
If I wanted to examine differences in the average scores of a sample over time or across trials. For example, if I wanted to determine whether a sample of high school students is more likely to use drugs before experiencing a drug-prevention course, right after finishing a drug-prevention course, or 6 months after finishing a drug prevention course, a repeated-measures ANOVA would be appropriate.
What kinds of variables are required to perform a mixed-model ANOVA that has both within-subject and between-subjects effects?
A dependent variable measured with an interval/ratio scale, at least one independent variable that is categorical/nominal (e.g., gender), and one variable that is measured at least twice for the within-subjects factor.
Suppose that I am the efficiency-control manager at a fast-food restaurant. Part of my job is to determine how long it takes to get orders to our customers. I want to know whether our efficiency changes across all 100 of our restaurants over a 6-month period. I collect data to figure out the average length of time it takes to get orders to customers at the beginning of the 6-month period, three months into the study period, and at the end of the 6-month period. I get the following data (in seconds per order):
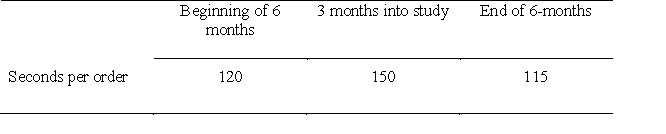 a. Create a line graph to represent the data presented in the table above.
a. Create a line graph to represent the data presented in the table above.
b. Interpret this graph. What does it tell you?
c. Now that I have seen my results and they suggest that we got slower in the middle of the study, I want to know whether this slow-down was consistent across the different regions where we have restaurants. So suppose I divide the restaurants into those in the east coast of the United States and those on the west coast. I get the following results:
 Create a line graph of these means.
Create a line graph of these means.
d. What is the between-subjects variable in this mixed-model ANOVA?
e. Looking at the data presented in the table and figure above, do you think there is a time X region interaction on the dependent variable?
f. Suppose that the ANOVA results produced a value for the interaction between Time of Assessment and Seconds per order of F(2,98) = 4.36. Using an alpha level of .05, is this a statistically significant interaction?
 a. Create a line graph to represent the data presented in the table above.
a. Create a line graph to represent the data presented in the table above.b. Interpret this graph. What does it tell you?
c. Now that I have seen my results and they suggest that we got slower in the middle of the study, I want to know whether this slow-down was consistent across the different regions where we have restaurants. So suppose I divide the restaurants into those in the east coast of the United States and those on the west coast. I get the following results:
 Create a line graph of these means.
Create a line graph of these means.d. What is the between-subjects variable in this mixed-model ANOVA?
e. Looking at the data presented in the table and figure above, do you think there is a time X region interaction on the dependent variable?
f. Suppose that the ANOVA results produced a value for the interaction between Time of Assessment and Seconds per order of F(2,98) = 4.36. Using an alpha level of .05, is this a statistically significant interaction?
a.
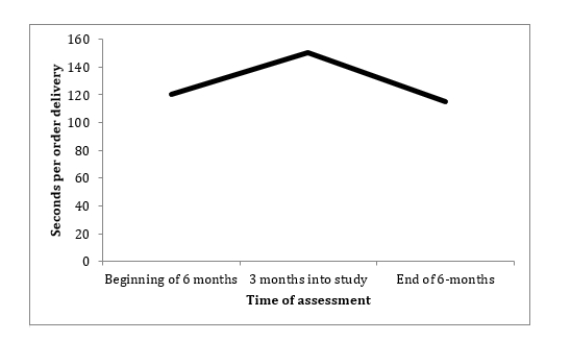 b. It appears that, on average across the 100 restaurants, it took longer to deliver orders to customers in the middle of the 6-month period of this study than it did at the beginning or the end. We would need to calulate the F value to determine whether this difference across the three time points is statistically significant.
b. It appears that, on average across the 100 restaurants, it took longer to deliver orders to customers in the middle of the 6-month period of this study than it did at the beginning or the end. We would need to calulate the F value to determine whether this difference across the three time points is statistically significant.
c.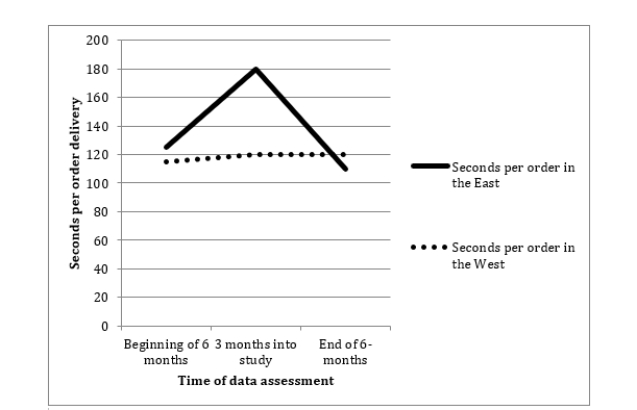 d. Region of the country that the restaurants were in.
d. Region of the country that the restaurants were in.
e. The seconds-per-order in the West remained relatively flat across the three times of data collection, but in the East the seconds-per-order was higher in the second data-collection point than it was in the first or last data collection point.
f. Looking in Appendix C, with 2 and 100 degrees of freedom, the critical F value is 3.09. Because this critical F value is smaller than our observed F value of 4.36, we would conclude that this is a statistically significant interaction.
 b. It appears that, on average across the 100 restaurants, it took longer to deliver orders to customers in the middle of the 6-month period of this study than it did at the beginning or the end. We would need to calulate the F value to determine whether this difference across the three time points is statistically significant.
b. It appears that, on average across the 100 restaurants, it took longer to deliver orders to customers in the middle of the 6-month period of this study than it did at the beginning or the end. We would need to calulate the F value to determine whether this difference across the three time points is statistically significant.c.
 d. Region of the country that the restaurants were in.
d. Region of the country that the restaurants were in.e. The seconds-per-order in the West remained relatively flat across the three times of data collection, but in the East the seconds-per-order was higher in the second data-collection point than it was in the first or last data collection point.
f. Looking in Appendix C, with 2 and 100 degrees of freedom, the critical F value is 3.09. Because this critical F value is smaller than our observed F value of 4.36, we would conclude that this is a statistically significant interaction.


