Deck 5: Z-Scores and Other Standard Scores
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/51
Play
Full screen (f)
Deck 5: Z-Scores and Other Standard Scores
1
Which of the following statements is NOT true regarding z-scores?
A) They describe an average amount that an entire distribution of scores deviates from the mean.
B) They describe how far a particular raw score deviates from the mean.
C) They are in standard deviation units.
D) Negative z-scores reflect deviations below the mean.
A) They describe an average amount that an entire distribution of scores deviates from the mean.
B) They describe how far a particular raw score deviates from the mean.
C) They are in standard deviation units.
D) Negative z-scores reflect deviations below the mean.
A
2
The mean of a z-score distribution is
A) 10.
B) 5.
C) 1.
D) 0.
A) 10.
B) 5.
C) 1.
D) 0.
D
3
The standard deviation of a z-score distribution is
A) 10.
B) 5.
C) 1.
D) 0.
A) 10.
B) 5.
C) 1.
D) 0.
C
4
A z-score is a
A) measure of variability.
B) measure of central tendency.
C) type of standard score.
D) type of raw score.
A) measure of variability.
B) measure of central tendency.
C) type of standard score.
D) type of raw score.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
5
The mean of a z-score distribution is _________ and the standard deviation is __________.
A) 1; 0
B) 0; 1
C) 100; 1
D) 1; 100
A) 1; 0
B) 0; 1
C) 100; 1
D) 1; 100

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
6
A z-score provides information about
A) the distribution's overall variability.
B) a person's relative position in a distribution.
C) the most representative value in a distribution.
D) the range of scores in a distribution.
A) the distribution's overall variability.
B) a person's relative position in a distribution.
C) the most representative value in a distribution.
D) the range of scores in a distribution.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
7
If a person earned 98 points on an exam, you can be certain that
A) the person did quite well.
B) the person did quite poorly.
C) the person passed with flying colors.
D) "a" and "c" are both true.
E) more information is needed.
A) the person did quite well.
B) the person did quite poorly.
C) the person passed with flying colors.
D) "a" and "c" are both true.
E) more information is needed.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
8
A distribution has μ = 40 and σ= 5. Yan scored two standard deviations above the mean. Yan's score was ________.
A) 45
B) 50
C) 55
D) 60
A) 45
B) 50
C) 55
D) 60

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
9
If someone obtains a z-score close to 0, that would indicate that
A) the person scored close to the mean.
B) the person scored very low.
C) there was very little variability in the distribution.
D) the person scored better than most.
A) the person scored close to the mean.
B) the person scored very low.
C) there was very little variability in the distribution.
D) the person scored better than most.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
10
A distribution has a mean of 100 and a standard deviation of 10. Sarah has a z-score of -2.00. What is her raw score?
A) 120
B) 10
C) 90
D) 80
A) 120
B) 10
C) 90
D) 80

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
11
An exam has a mean of 75 and a standard deviation of 8. What exam score is 1.5 standard deviations above the mean?
A) 83.5
B) 76.5
C) 87
D) 91
A) 83.5
B) 76.5
C) 87
D) 91

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
12
In a distribution with μ = 68 and σ = 4, Curtis scored two standard deviations above the mean. His raw score is ________.
A) 70
B) 72
C) 74
D) 76
A) 70
B) 72
C) 74
D) 76

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
13
The numerator in the formula for a z-score is
A) a deviation score.
B) the standard deviation.
C) SS
D) ∑X²
A) a deviation score.
B) the standard deviation.
C) SS
D) ∑X²

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
14
The denominator in the formula for a z-score is
A) a deviation score.
B) the standard deviation.
C) SS
D) ∑X²
A) a deviation score.
B) the standard deviation.
C) SS
D) ∑X²

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
15
A person's raw score is 6 points below the mean and has a z-score of -2. What is the standard deviation for that distribution?
A) 12
B) 9
C) 3
D) -12
A) 12
B) 9
C) 3
D) -12

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
16
A distribution has a mean of 36 and a standard deviation of 2.5. Jeremy scored 32. What is his z-score?
A) -.63
B) 63
C) -1.6
D) 1.6
A) -.63
B) 63
C) -1.6
D) 1.6

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
17
A distribution has a mean of 50 and a standard deviation of 10. Robin scored 35. What is her equivalent z-score?
A) -1.5
B) -15
C) -.67
D) -2
A) -1.5
B) -15
C) -.67
D) -2

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
18
If we wanted to see a person's relative standing from scores on two different tests,
A) we would compare the person's raw scores to the means of each distribution.
B) both of the person's raw scores would have to be transformed into z-scores.
C) the standard deviations would have to be the same for both distributions.
D) It cannot be done if the means and standards deviations are different for each distribution.
A) we would compare the person's raw scores to the means of each distribution.
B) both of the person's raw scores would have to be transformed into z-scores.
C) the standard deviations would have to be the same for both distributions.
D) It cannot be done if the means and standards deviations are different for each distribution.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
19
If a person has a z-score of -2.00, this would mean that they
A) scored two points higher than the mean.
B) scored two standard deviations above the mean.
C) scored two points lower than the mean.
D) scored two standard deviations below the mean.
A) scored two points higher than the mean.
B) scored two standard deviations above the mean.
C) scored two points lower than the mean.
D) scored two standard deviations below the mean.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
20
A distribution has a μ = 46 and a σ = 4. What is the equivalent raw score for a person with a z-score of 1.5?
A) 54
B) 52
C) 50
D) 40
A) 54
B) 52
C) 50
D) 40

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following z-scores is closest to the mean?
A) -.10
B) +.12
C) -1.00
D) +1.00
A) -.10
B) +.12
C) -1.00
D) +1.00

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following z-scores is furthest away from the mean?
A) -1.00
B) 0
C) -.50
D) +2.00
A) -1.00
B) 0
C) -.50
D) +2.00

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
23
A set of scores has a standard deviation of 6. A raw score of 53 converts to a z-score of -1.5. What is the mean of the distribution?
A) 56
B) 62
C) 65
D) 51.5
A) 56
B) 62
C) 65
D) 51.5

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
24
A set of scores has a σ = 4. Susan's score was 93 which converted to a z-score of +2.00. What was the mean of the distribution?
A) 77
B) 81
C) 85
D) 89
A) 77
B) 81
C) 85
D) 89

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
25
Hans scored 16 points above the mean with a z-score of +2.00. What was the standard deviation for the distribution?
A) 8
B) 14
C) 18
D) 32
A) 8
B) 14
C) 18
D) 32

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
26
A set of scores has a mean of 75. Jiang's score of 60 converted to a z-score of -1.5. What was the standard deviation of the distribution?
A) 5
B) 10
C) 15
D) 20
A) 5
B) 10
C) 15
D) 20

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
27
A set of scores has a mean of 36 and a standard deviation of 6. Karim's z-score was -1.50. What was his raw score?
A) 30
B) 24
C) 27
D) 34.5
A) 30
B) 24
C) 27
D) 34.5

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
28
Julie's z-score was +2.50 in a distribution whose μ = 100 with a σ = 10. What was Julie's raw score?
A) 102.5
B) 110
C) 115
D) 125
A) 102.5
B) 110
C) 115
D) 125

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
29
A set of scores has a μ = 65 and a σ = 12. Lucinda's z-score was +1.50. What was her raw score?
A) 53
B) 77
C) 83
D) 89
A) 53
B) 77
C) 83
D) 89

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
30
Elijah's z-score was -.25 in a distribution where the mean was 70 and the standard deviation was 8. What is his raw score?
A) 68
B) 65
C) 69.75
D) 72
A) 68
B) 65
C) 69.75
D) 72

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
31
The WAIS has a mean of 100 and a standard deviation of 15. One of the requirements to become a member of MENSA, an organization for smart people, is to score a minimum of two standard deviations above the mean on this test. What is the minimum score requirement?
A) 120
B) 130
C) 145
D) 150
A) 120
B) 130
C) 145
D) 150

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the following statistics would be helpful for comparing the scores from two different distributions?
A) range
B) interquartile range
C) standard deviation
D) z-score
A) range
B) interquartile range
C) standard deviation
D) z-score

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
33
The mean for a statistics exam was 85. Karen calculated her own z-score to be +1.75 for her test result of 68 points. What is wrong with Karen's calculation?
A) A z-score cannot be calculated for ratio level data.
B) A z-score cannot be calculated for individual score results.
C) Her z-score should be negative.
D) Not enough information is provided.
A) A z-score cannot be calculated for ratio level data.
B) A z-score cannot be calculated for individual score results.
C) Her z-score should be negative.
D) Not enough information is provided.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
34
Jorge scored 70 on an exam and his z-score was -2.00. Michelle scored 82 on the same test and her z-score was +1.00. What was the mean of the exam?
A) 74
B) 78
C) 84
D) Not enough information is provided.
A) 74
B) 78
C) 84
D) Not enough information is provided.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
35
Isabelle scored 98 on an exam and her z-score was +3.00. Isaac scored 80 on the same exam and his z-score was -3.00. What was the mean of the exam?
A) 89
B) 92
C) 93
D) 86
A) 89
B) 92
C) 93
D) 86

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
36
If one z-score from a distribution is -1 for a raw score of 66 and another z-score is +3 for a raw score of 78, what is the standard deviation for the distribution?
A) 2
B) 4
C) 3
D) 6
A) 2
B) 4
C) 3
D) 6

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
37
Ariana's raw score of 33 on her philosophy exam converted to a z-score of -1.50. Claire's raw score on the same exam was 48 and it converted to a z-score of +1.00. What was the standard deviation for the distribution?
A) 3
B) 6
C) 9
D) Not enough information is provided.
A) 3
B) 6
C) 9
D) Not enough information is provided.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
38
You scored at the mean on your statistics exam. What is your z-score?
A) 0
B) 100
C) +1.00
D) Not enough information is provided.
A) 0
B) 100
C) +1.00
D) Not enough information is provided.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
39
To change a raw score to a z-score, you need to
A) specify a new mean and standard deviation.
B) convert all of the raw scores into z-scores.
C) use the TSS formula.
D) know the mean and standard deviation of the distribution.
A) specify a new mean and standard deviation.
B) convert all of the raw scores into z-scores.
C) use the TSS formula.
D) know the mean and standard deviation of the distribution.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
40
To use the TSS formula,
A) raw scores have to first be converted to z-scores.
B) a mean has to be specified.
C) a standard deviation has to be specified.
D) All of the above are true.
A) raw scores have to first be converted to z-scores.
B) a mean has to be specified.
C) a standard deviation has to be specified.
D) All of the above are true.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
41
Amar's raw score of 80 converted to a standard score of +1.63. In terms of location in the distribution,
A) Amar's standard score will be +1.63 standard deviations above 80.
B) Amar's standard score and his raw score will be at the same location in the distribution.
C) Amar's raw score will be 1.63 standard deviations above the mean of the distribution.
D) Both "a" and "b" are correct.
E) Both "b" and "c" are correct.
A) Amar's standard score will be +1.63 standard deviations above 80.
B) Amar's standard score and his raw score will be at the same location in the distribution.
C) Amar's raw score will be 1.63 standard deviations above the mean of the distribution.
D) Both "a" and "b" are correct.
E) Both "b" and "c" are correct.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
42
Briefly define the following terms:
a. z-score
b. Standard score
c. Transformed standard score
a. z-score
b. Standard score
c. Transformed standard score

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
43
Olivia's score was 75 on both her government and history exams. The class mean for the government exam was 80 with a standard deviation of 5. The class mean for the history exam was 70 with a standard deviation of 4. Calculate Olivia's z-scores. On which exam did she perform better?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
44
The average weight of a popular brand of snack crackers is 12.4 ounces with a standard deviation of .3 ounce. The box you purchase weighs 12.8 ounces. What is the z-score for your box of crackers?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
45
Colby's speed was 24 minutes for his most recent 5K race and his z-score was -2.00. The standard deviation for the race was 4 minutes. What was the mean?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
46
Three friends, who are also very competitive, enrolled in three different sections of the same history course. Their raw scores on the first test, along with the means and standard deviations of their respective sections, are listed below.
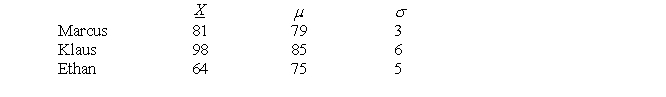 a. Who gets bragging rights? Explain.
a. Who gets bragging rights? Explain.
b. Who should devise a new study strategy? Explain.
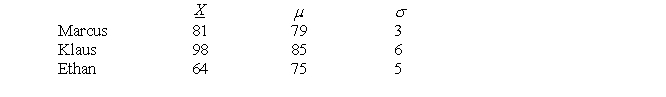 a. Who gets bragging rights? Explain.
a. Who gets bragging rights? Explain.b. Who should devise a new study strategy? Explain.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
47
As a part of learning how to administer various tests, students taking a course in psychological measurement were administered the Wechsler IQ test. The mean for the course was 106 and the standard deviation was 11. The scores are listed below for three students. What are their equivalent standardized Wechsler IQ scores?
a. Student One: X = 98
b. Student Two: X = 108
c. Student Three: X = 110
a. Student One: X = 98
b. Student Two: X = 108
c. Student Three: X = 110

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
48
Wayne is developing a new assessment instrument, called HOPE, designed to measure peoples' degree of optimism. He will standardize the test with a mean of 75 and a standard deviation of 8. As a preliminary measure, Wayne administers the HOPE scale to a group of volunteers. The mean for the group was 110 and the standard deviation was 6. The scores for two of the volunteers are below.
a. Rylee scored 107. What was her HOPE score?
b. Haru scored 115. What was his HOPE score?
a. Rylee scored 107. What was her HOPE score?
b. Haru scored 115. What was his HOPE score?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
49
A set of population scores along with some summary information is listed below.
 a. What is the z-score for a raw score of 8?
a. What is the z-score for a raw score of 8?
b. What is the z-score for a raw score of 3?
 a. What is the z-score for a raw score of 8?
a. What is the z-score for a raw score of 8?b. What is the z-score for a raw score of 3?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
50
Given the following quiz scores: 10, 9, 8, 7, 6
a. What is the z-score for a raw score of 7?
b. What is the z-score for a raw score of 10?
a. What is the z-score for a raw score of 7?
b. What is the z-score for a raw score of 10?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
51
A set of scores has a mean of 58.23 and a standard deviation of 3.12. Lilly scored -.83 standard deviations below the mean and Karina scored 1.53 standard deviations above the mean.
a. What was Lilly's raw score?
b. What was Karina's raw score?
a. What was Lilly's raw score?
b. What was Karina's raw score?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck


