Deck 4: Subspaces
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/60
Play
Full screen (f)
Deck 4: Subspaces
1
Determine if S is a subspace of R2, where S is the subset consisting of all vectors
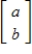 where
where
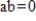
.
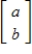 where
where 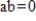
.
S is not a subspace.
2
Determine if S is a subspace of R3, where S is the subset consisting of all vectors
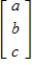 where
where
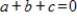
.
 where
where 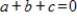
.
S is a subspace.
3
Determine if S is a subspace of R3, where S is the subset consisting of all vectors
 where
where
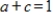
.
 where
where 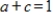
.
S is not a subspace.
4
Determine if S is a subspace of R, where S is the subset consisting of all vectors
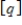 where q is a rational number.
where q is a rational number.
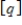 where q is a rational number.
where q is a rational number.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
5
Determine the null space of
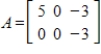
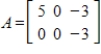

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
6
Determine the null space of
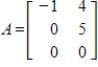
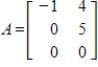

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
7
Determine the null space of
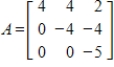
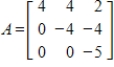

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
8
Determine the null space of
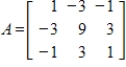
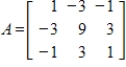

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
9
Let
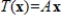 for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T.
for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T. 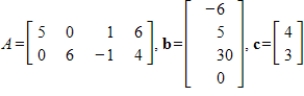
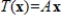 for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T.
for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T. 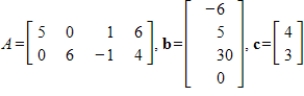

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
10
Let
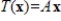 for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T.
for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T. 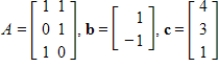
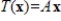 for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T.
for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T. 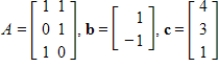

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
11
If
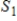
,
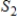
, and
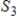 are subspaces of Rn, then their intersection
are subspaces of Rn, then their intersection
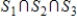 is also a subspace of Rn.
is also a subspace of Rn.
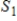
,
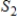
, and
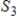 are subspaces of Rn, then their intersection
are subspaces of Rn, then their intersection 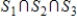 is also a subspace of Rn.
is also a subspace of Rn.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
12
Let A be an
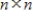 invertible matrix, let b be an
invertible matrix, let b be an
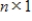 column vector. Let S be the set of all vectors x such that
column vector. Let S be the set of all vectors x such that
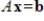
. Then S is a subspace of Rn.
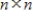 invertible matrix, let b be an
invertible matrix, let b be an 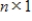 column vector. Let S be the set of all vectors x such that
column vector. Let S be the set of all vectors x such that 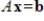
. Then S is a subspace of Rn.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
13
The null space of an
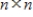 matrix A is a subspace of Rn if and only if A is invertible.
matrix A is a subspace of Rn if and only if A is invertible.
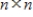 matrix A is a subspace of Rn if and only if A is invertible.
matrix A is a subspace of Rn if and only if A is invertible.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
14
Let A be an
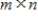 matrix, and B an
matrix, and B an
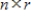 matrix. Then the null space of B is a subspace of the null space of AB.
matrix. Then the null space of B is a subspace of the null space of AB.
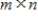 matrix, and B an
matrix, and B an 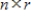 matrix. Then the null space of B is a subspace of the null space of AB.
matrix. Then the null space of B is a subspace of the null space of AB.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
15
Let A be an m×nmatrix, and B an m×rmatrix. Then the range of AB is a subspace of the range of

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
16
By forming matrix rows, find a basis for the given subspace S and give the dimension of S, where
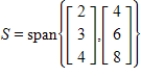


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
17
By forming matrix rows, find a basis for the given subspace S and give the dimension of S, where
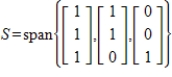
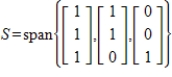

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
18
By forming matrix rows, find a basis for the given subspace S and give the dimension of S, where
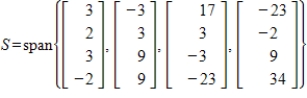
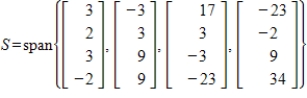

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
19
Find a basis for the given subspace S by deleting linearly dependent vectors, and give the dimension of S. No actual computation is needed.
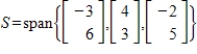
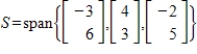

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
20
By forming matrix columns, find a basis for the given subspace S and give the dimension of S, where
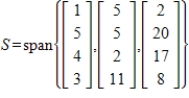


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
21
By forming matrix columns, find a basis for the given subspace S and give the dimension of S, where
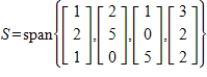
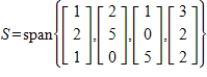

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
22
Expand the given set to form a basis for R3.
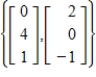
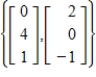

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
23
Expand the given set to form a basis for R4.
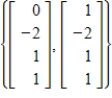


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
24
Find a basis for the null space of the given matrix A and give
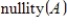
.
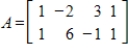
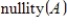
.
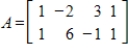

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
25
Find a basis for the null space of the given matrix A and give
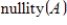
.
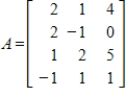
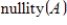
.
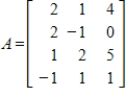

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
26
If
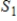 and
and
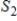 are subspaces of Rn, with
are subspaces of Rn, with
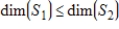
, then
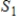 is a subset of
is a subset of
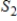
.
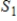 and
and 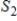 are subspaces of Rn, with
are subspaces of Rn, with 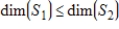
, then
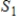 is a subset of
is a subset of 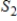
.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
27
If 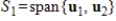 and
and 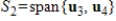
, then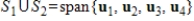 .
.
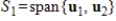 and
and 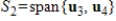
, then
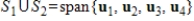 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
28
If
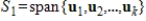 and
and
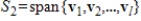
, and
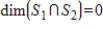
, then
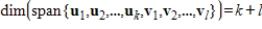
.
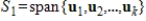 and
and 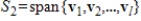
, and
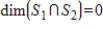
, then
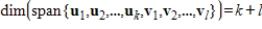
.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
29
If E is an
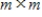 elementary matrix and A is an
elementary matrix and A is an
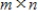 matrix, then the subspace spanned by the columns of A is the same as the subspace spanned by the columns of EA.
matrix, then the subspace spanned by the columns of A is the same as the subspace spanned by the columns of EA.
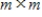 elementary matrix and A is an
elementary matrix and A is an 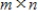 matrix, then the subspace spanned by the columns of A is the same as the subspace spanned by the columns of EA.
matrix, then the subspace spanned by the columns of A is the same as the subspace spanned by the columns of EA.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
30
If E is an
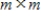 elementary matrix and A is an
elementary matrix and A is an
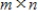 matrix, then the subspace spanned by the rows of A is the same as the subspace spanned by the rows of EA.
matrix, then the subspace spanned by the rows of A is the same as the subspace spanned by the rows of EA.
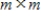 elementary matrix and A is an
elementary matrix and A is an 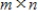 matrix, then the subspace spanned by the rows of A is the same as the subspace spanned by the rows of EA.
matrix, then the subspace spanned by the rows of A is the same as the subspace spanned by the rows of EA.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
31
Find bases for the column space of A, the row space of A, and the null space of A. 


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
32
Find bases for the column space of A, the row space of A, and the null space of A. 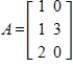
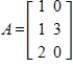

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
33
Find bases for the column space of A, the row space of A, and the null space of A. 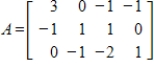
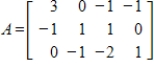

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
34
Find all values of
 so that rank
so that rank
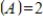
, where
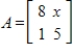
 so that rank
so that rank 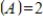
, where
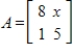

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
35
Find all values of
 so that rank
so that rank
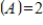
, where
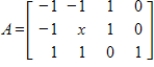
 so that rank
so that rank 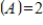
, where
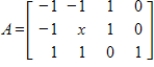

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
36
Suppose that
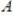 is a
is a
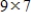 matrix. If the dimension of
matrix. If the dimension of
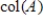 is
is
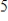
, what are the dimensions of
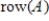 and
and
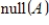
?
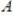 is a
is a 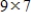 matrix. If the dimension of
matrix. If the dimension of 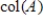 is
is 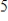
, what are the dimensions of
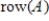 and
and 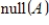
?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
37
Suppose that A is a
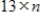 matrix. If the dimension of
matrix. If the dimension of
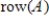 is
is
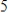
, and the dimension of
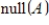 is
is

, what is

?
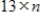 matrix. If the dimension of
matrix. If the dimension of 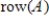 is
is 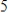
, and the dimension of
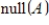 is
is 
, what is

?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose that A is a
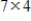 matrix and that
matrix and that
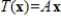
. If
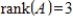
, what is the dimension of the kernel of T ?
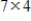 matrix and that
matrix and that 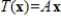
. If
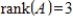
, what is the dimension of the kernel of T ?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose that A is a
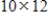 matrix, and that B is an equivalent matrix in echelon form. If B has
matrix, and that B is an equivalent matrix in echelon form. If B has
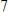 pivot columns, what is
pivot columns, what is
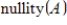
?
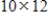 matrix, and that B is an equivalent matrix in echelon form. If B has
matrix, and that B is an equivalent matrix in echelon form. If B has 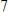 pivot columns, what is
pivot columns, what is 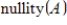
?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose that A is an
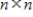 matrix. If
matrix. If
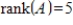
, and
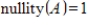
, what is

?
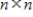 matrix. If
matrix. If 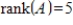
, and
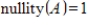
, what is

?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
41
If A and B are equivalent matrices, then
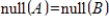
.
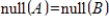
.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
42
If
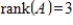 and
and
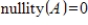
, then
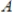 is a
is a
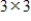 matrix.
matrix.
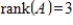 and
and 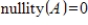
, then
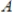 is a
is a 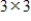 matrix.
matrix.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
43
If T is a one-to-one linear transformation from R3 to R5, and A is a matrix such that
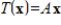
, then
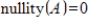
.
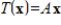
, then
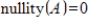
.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
44
If T is an onto linear transformation from R3 to R5, and A is a matrix such that
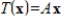
, then
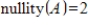
.
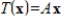
, then
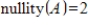
.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
45
If A is an
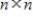 matrix such that
matrix such that
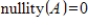
, then
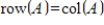
.
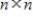 matrix such that
matrix such that 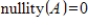
, then
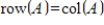
.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
46
Convert the coordinate vector
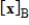 from the given basis B to the standard basis.
from the given basis B to the standard basis.
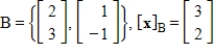
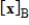 from the given basis B to the standard basis.
from the given basis B to the standard basis.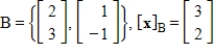

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
47
Convert the coordinate vector
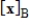 from the given basis B to the standard basis.
from the given basis B to the standard basis.
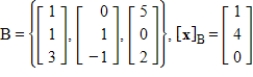
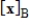 from the given basis B to the standard basis.
from the given basis B to the standard basis.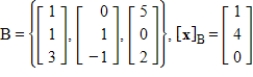

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
48
Find the change of basis matrix from the standard basis to B, and then convert x to the coordinate vector with respect to B. 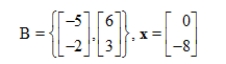
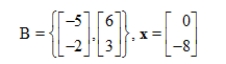

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
49
Find the change of basis matrix from the standard basis to B, and then convert x to the coordinate vector with respect to B. 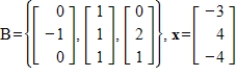
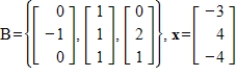

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
50
Find the change of basis matrix from B1 to B2.
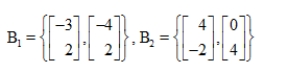
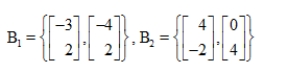

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
51
Find the change of basis matrix from B1 to B2.
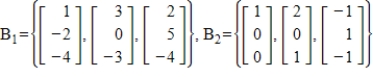
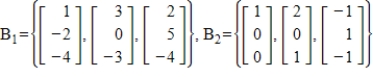

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
52
Find the change of basis matrix from B2 to B1.
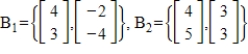
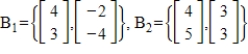

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
53
Find the change of basis matrix from B2 to B1.
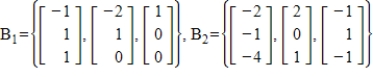
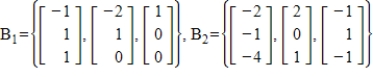

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
54
Find the change of basis matrix from B1 to B2.
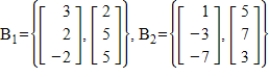
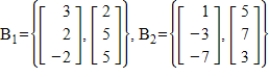

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
55
Find
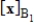 given
given
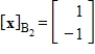
, where
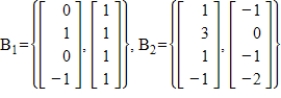
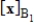 given
given 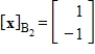
, where
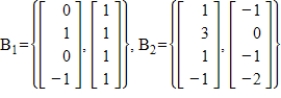

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
56
If B is a basis, then
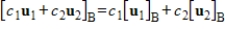 for all scalars
for all scalars
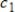
,
 and all vectors
and all vectors
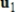
,
 in span (B).
in span (B).
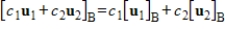 for all scalars
for all scalars 
,
 and all vectors
and all vectors 
,
 in span (B).
in span (B).
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
57
If B1, B2, and B3 are all bases for a given subspace, A is the change of basis matrix from B1 to B2, and B is the change of basis matrix from B2 to B3, then the change of basis matrix from B1 to B3 is given by BA.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
58
If B1, B2 are bases for a given subspace, and A is the change of basis matrix from B1 to B2, then A is invertible, and
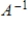 is the change of basis matrix from B2 to B1.
is the change of basis matrix from B2 to B1.
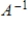 is the change of basis matrix from B2 to B1.
is the change of basis matrix from B2 to B1.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
59
If B is a basis for a given subspace, and u and v are vectors in span (B) such that
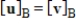
, then

.
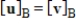
, then

.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
60
If B is a basis for a given subspace, and u is in span (B) with
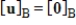
, then
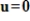
.
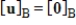
, then
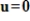
.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck


