Deck 2: Euclidean Space
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/48
Play
Full screen (f)
Deck 2: Euclidean Space
1
Determine
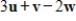
, where
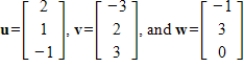
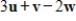
, where
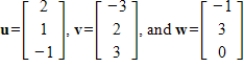
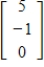
2
Express the given vector equation as a system of linear equations.
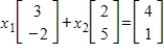
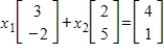
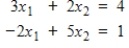
3
Express the given vector equation as a system of linear equations.
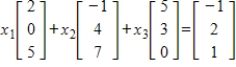
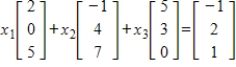
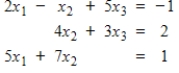
4
Express the given system of linear equations as a single vector equation.
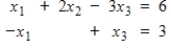
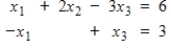

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
5
Express the given system of linear equations as a single vector equation.
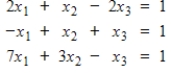
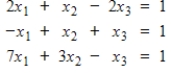

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
6
The general solution to a linear system is given. Express this solution as a linear combination of vectors.
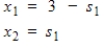
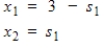

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
7
The general solution to a linear system is given. Express this solution as a linear combination of vectors.
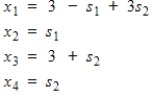
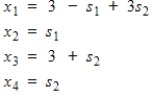

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
8
Find the unknowns in the given vector equation.
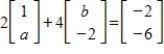
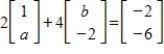

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
9
Find the unknowns in the given vector equation.
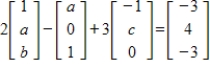
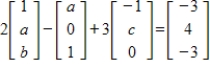

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
10
Express
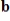 as a linear combination of the other vectors, if possible.
as a linear combination of the other vectors, if possible.
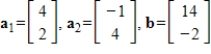
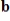 as a linear combination of the other vectors, if possible.
as a linear combination of the other vectors, if possible.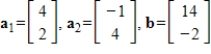

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
11
Express
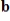 as a linear combination of the other vectors, if possible.
as a linear combination of the other vectors, if possible.
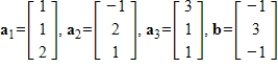
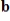 as a linear combination of the other vectors, if possible.
as a linear combination of the other vectors, if possible.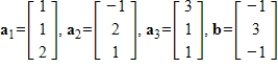

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
12
If
 and
and
 are vectors, and
are vectors, and
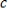 and
and
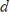 are scalars, then
are scalars, then
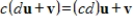
.
 and
and  are vectors, and
are vectors, and 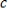 and
and 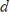 are scalars, then
are scalars, then 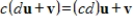
.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
13
If

,

, and
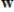 are vectors, then
are vectors, then
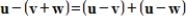
.

,

, and
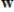 are vectors, then
are vectors, then 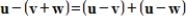
.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
14
If
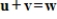
, then
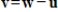
.
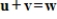
, then
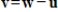
.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
15
Sketch the graph of
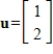 and
and
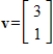
, and then use the Parallelogram Rule to sketch the graph of
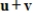
.
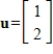 and
and 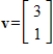
, and then use the Parallelogram Rule to sketch the graph of
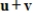
.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
16
Determine how to divide a total mass of 18 kg among the vectors
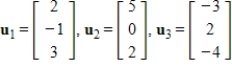 so that the center of mass is
so that the center of mass is

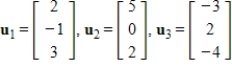 so that the center of mass is
so that the center of mass is

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
17
Find an example of a linear system with two equations and three variables that has
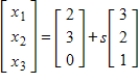 as the general solution.
as the general solution.
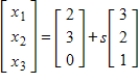 as the general solution.
as the general solution.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
18
Find four vectors that are in the span of the given vectors.
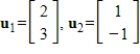
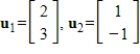

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
19
Find five vectors that are in the span of the given vectors.
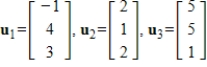
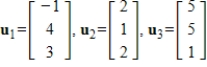

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
20
Determine if
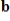 is in the span of the other given vectors. If so, write
is in the span of the other given vectors. If so, write
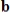 as a linear combination of the other vectors.
as a linear combination of the other vectors.
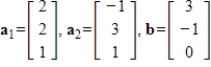
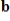 is in the span of the other given vectors. If so, write
is in the span of the other given vectors. If so, write 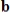 as a linear combination of the other vectors.
as a linear combination of the other vectors.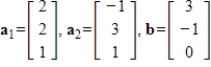

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
21
Determine if
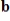 is in the span of the other given vectors. If so, write
is in the span of the other given vectors. If so, write
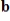 as a linear combination of the other vectors.
as a linear combination of the other vectors.
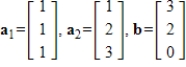
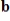 is in the span of the other given vectors. If so, write
is in the span of the other given vectors. If so, write 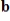 as a linear combination of the other vectors.
as a linear combination of the other vectors.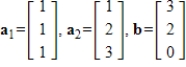

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
22
Find
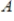
,

, and
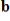 such that
such that
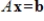 corresponds to the given linear system.
corresponds to the given linear system.
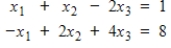
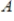
,

, and
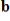 such that
such that 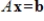 corresponds to the given linear system.
corresponds to the given linear system.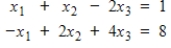

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
23
Find
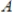
,

, and
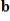 such that
such that
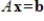 corresponds to the given linear system.
corresponds to the given linear system.
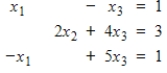
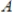
,

, and
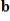 such that
such that 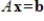 corresponds to the given linear system.
corresponds to the given linear system.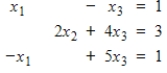

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
24
Express the given system of linear equations as a vector equation.
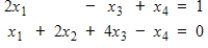
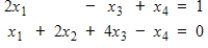

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
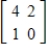
25
Determine if the columns of the given matrix span R2.


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
26
Determine if the columns of the given matrix span R3.



Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
27
Determine if the system
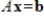 (where
(where
 and
and
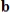 have the appropriate number of components) has a solution for all choices of
have the appropriate number of components) has a solution for all choices of
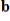
.
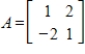
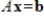 (where
(where  and
and 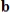 have the appropriate number of components) has a solution for all choices of
have the appropriate number of components) has a solution for all choices of 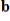
.
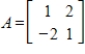

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
28
Find all values of
 such that the vectors span R2.
such that the vectors span R2.
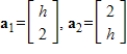
 such that the vectors span R2.
such that the vectors span R2.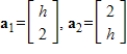

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
29
For what value(s) of h do the given vectors span
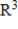
?
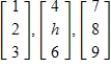
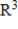
?
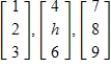

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose a matrix
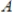 has
has
 rows and
rows and
 columns, with
columns, with
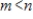
. Then the columns of
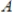 do not span Rn.
do not span Rn.
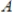 has
has  rows and
rows and  columns, with
columns, with 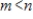
. Then the columns of
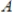 do not span Rn.
do not span Rn.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
31
Suppose a matrix
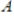 has
has
 rows and
rows and
 columns, with
columns, with
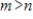
. Then the columns of
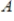 span Rn.
span Rn.
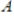 has
has  rows and
rows and  columns, with
columns, with 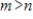
. Then the columns of
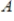 span Rn.
span Rn.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
32
If the columns of a matrix
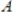 with
with
 rows and
rows and
 columns do not span Rn, then there exists a vector
columns do not span Rn, then there exists a vector
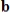 in Rn such that
in Rn such that
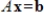 does not have a solution.
does not have a solution.
 with
with  rows and
rows and  columns do not span Rn, then there exists a vector
columns do not span Rn, then there exists a vector 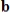 in Rn such that
in Rn such that 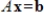 does not have a solution.
does not have a solution.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
33
If the columns of a matrix
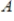 with
with
 rows and
rows and
 columns spans Rn, then
columns spans Rn, then
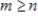
.
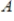 with
with  rows and
rows and  columns spans Rn, then
columns spans Rn, then 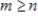
.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
34
Determine if the given vectors are linearly independent.
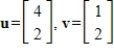
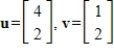

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
35
Determine if the given vectors are linearly independent.
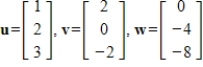
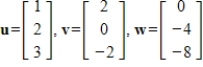

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
36
Determine if the given vectors are linearly independent.
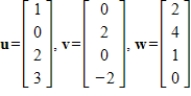
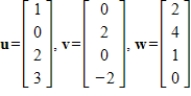

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
37
Determine if the columns of the given matrix are linearly independent.
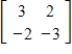
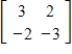

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
38
Determine if the columns of the given matrix are linearly independent.
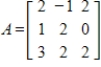
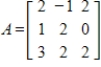

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
39
Determine if the columns of the given matrix are linearly independent.
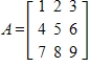
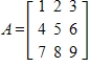

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
40
Determine if the homogeneous system
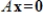 has any nontrivial solutions, where
has any nontrivial solutions, where
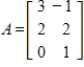
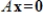 has any nontrivial solutions, where
has any nontrivial solutions, where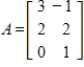

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
41
Determine if the homogeneous system
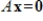 has any nontrivial solutions, where
has any nontrivial solutions, where
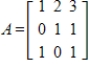
.
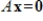 has any nontrivial solutions, where
has any nontrivial solutions, where 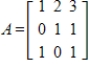
.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
42
Determine by inspection (that is, with only minimal calculations) if the given vectors form a linearly dependent or linearly independent set. Justify your answer.
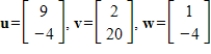
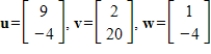

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
43
Determine if one of the given vectors is in the span of the other vectors.
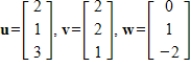
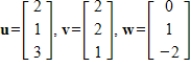

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
44
Suppose matrix
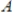 has
has
 rows and
rows and
 columns, with
columns, with
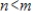
. Then the columns of
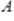 are linearly dependent.
are linearly dependent.
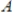 has
has  rows and
rows and  columns, with
columns, with 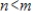
. Then the columns of
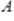 are linearly dependent.
are linearly dependent.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose a matrix
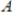 has
has
 rows and
rows and
 columns, with
columns, with
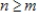
. Then the columns of
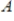 are linearly independent.
are linearly independent.
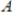 has
has  rows and
rows and  columns, with
columns, with 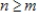
. Then the columns of
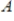 are linearly independent.
are linearly independent.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
46
Suppose there exists a vector
 such that
such that
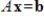
. Then the columns of
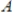 are linearly independent.
are linearly independent.
 such that
such that 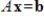
. Then the columns of
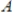 are linearly independent.
are linearly independent.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
47
If
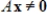 for every
for every
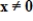
, then the columns of
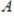 are linearly independent.
are linearly independent.
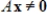 for every
for every 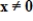
, then the columns of
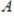 are linearly independent.
are linearly independent.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
48
If
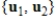
,
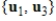
, and
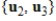 are all linearly independent, then
are all linearly independent, then
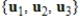 is linearly independent.
is linearly independent.
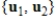
,
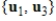
, and
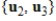 are all linearly independent, then
are all linearly independent, then 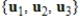 is linearly independent.
is linearly independent.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck


