Deck 18: Multiple Linear Regression
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/10
Play
Full screen (f)
Deck 18: Multiple Linear Regression
1
You are given the following data, where X1 (Pretest score) and X2 (Hours spent in the program) are used to predict Y (Posttest score):
Determine the following values: intercept, b1, b2, SSres, SSreg, F, sres2, s(b1), s(b2), t1, t2.
Determine the following values: intercept, b1, b2, SSres, SSreg, F, sres2, s(b1), s(b2), t1, t2.
Intercept = -70.662, b1 = 1.235, b2 = 8.077.
SSreg = 619.504, SSres = 44.496, F(2,3) = 20.884 (p < .017, reject at .05), s2res = 14.832.
s(b1) = .227, s(b2) = 1.660, t1 = 5.437 (p = .012, reject at .05), t2 = 4.866 (p = .017, reject at .05).
Procedure:
Create a data set with three variables: Posttest (Y), Pretest (X1), and Hour (X2). The data set should have six cases.
1) Go to Analyze Regression Linear.
2) Select Posttest to the Dependent list. Select Pretest and Hour to the Independent(s) list.
"3) Click OK.
Selected SPSS Output:
a. Predictors: (Constant), Hour, Fretest
b. Dependent Variable: Posttest Results:
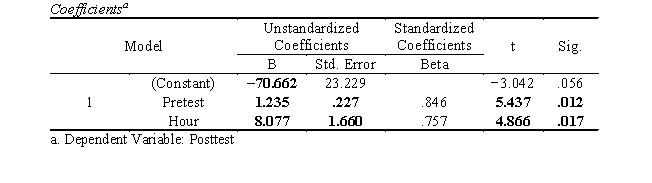
The results of the multiple linear regression suggest that a significant proportion of the total variation in posttest scores was effectively predicted by pretest scores and hours spent in the program, F(2,3) = 20.884, p = .017. For Pretest, the unstandardized partial slope (1.235) and standardized partial slope (.846) are statistically significantly different from 0 (t = 5.437, df = 3, p = .012); with every one-point increase in pretest, posttest score will increase by 1.235 when controlling for Hour. For Hour, the unstandardized partial slope (8.077) and standardized partial slope (.757) are statistically significantly different from 0 (t = 4.866, df = 3, p = .017); with every additional hour spent in the program, posttest score is expected to increase by 8.077 when controlling for Pretest scores. Thus, Pretest and Hour were shown to be statistically significant predictors of Posttest, both individually and collectively. Multiple R2 indicates that 93.3% of the variation in Salary was predicted by Pretest and Hour. This suggests a large effect size.
The intercept was -70.662, which is not statistically significantly different from 0 at the .05 level (t = -3.042, df = 3, p = .056)."
SSreg = 619.504, SSres = 44.496, F(2,3) = 20.884 (p < .017, reject at .05), s2res = 14.832.
s(b1) = .227, s(b2) = 1.660, t1 = 5.437 (p = .012, reject at .05), t2 = 4.866 (p = .017, reject at .05).
Procedure:
Create a data set with three variables: Posttest (Y), Pretest (X1), and Hour (X2). The data set should have six cases.
1) Go to Analyze Regression Linear.
2) Select Posttest to the Dependent list. Select Pretest and Hour to the Independent(s) list.
"3) Click OK.
Selected SPSS Output:
a. Predictors: (Constant), Hour, Fretest
b. Dependent Variable: Posttest Results:

The results of the multiple linear regression suggest that a significant proportion of the total variation in posttest scores was effectively predicted by pretest scores and hours spent in the program, F(2,3) = 20.884, p = .017. For Pretest, the unstandardized partial slope (1.235) and standardized partial slope (.846) are statistically significantly different from 0 (t = 5.437, df = 3, p = .012); with every one-point increase in pretest, posttest score will increase by 1.235 when controlling for Hour. For Hour, the unstandardized partial slope (8.077) and standardized partial slope (.757) are statistically significantly different from 0 (t = 4.866, df = 3, p = .017); with every additional hour spent in the program, posttest score is expected to increase by 8.077 when controlling for Pretest scores. Thus, Pretest and Hour were shown to be statistically significant predictors of Posttest, both individually and collectively. Multiple R2 indicates that 93.3% of the variation in Salary was predicted by Pretest and Hour. This suggests a large effect size.
The intercept was -70.662, which is not statistically significantly different from 0 at the .05 level (t = -3.042, df = 3, p = .056)."
2
Complete the missing information for this regression model (df = 25).
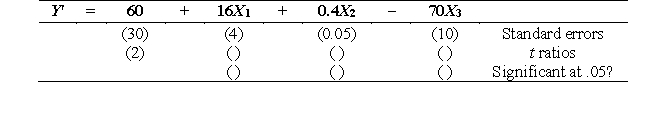
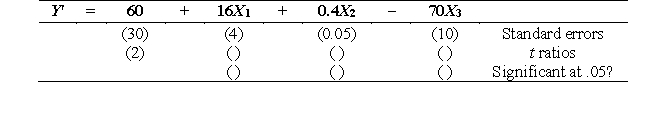
t1 = b1/s(b1) = 16/4 = 4; t2 = b2/s(b2) = .4/.05 = 8; t3 = b3/s(b3) = 70/10 = 7.
The critical t value is /2tdf = 0.025t25 = 2.06.
|t1|, |t2|, |t3| > critical t, so X1, X2, and X3 are all significant predictors of Y.
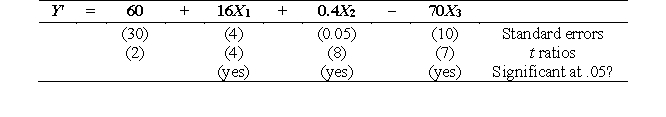
The critical t value is /2tdf = 0.025t25 = 2.06.
|t1|, |t2|, |t3| > critical t, so X1, X2, and X3 are all significant predictors of Y.
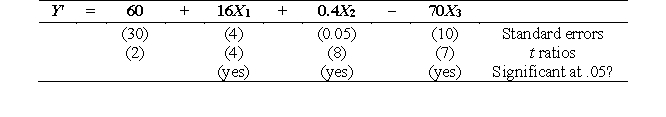
3
A researcher would like to predict GPA from a set of three predictor variables for a sample of 34 college students. Multiple linear regression analysis was utilized. Complete the following summary table
( = .05) for the test of significance of the overall regression model:

( = .05) for the test of significance of the overall regression model:

There are three independent variables, so m = 3. There are 34 students, so n = 34.
dfreg = m = 3, dfres = n - m -1 = 34 - 3 - 1 = 30, dftotal = n - 1 = 34 - 1 = 33.
SSreg = MSreg*dfreg = 6.5*3 = 19.5, SSres = SStotal- SSreg = 66 - 19.5 = 46.5.
MSres = SSres/dfres = 46.5/30 = 1.55
F = MSreg/MSres = 6.5/1.55 = 4.19; critical value = .05F3,30 = 2.92 < F, reject H0.

dfreg = m = 3, dfres = n - m -1 = 34 - 3 - 1 = 30, dftotal = n - 1 = 34 - 1 = 33.
SSreg = MSreg*dfreg = 6.5*3 = 19.5, SSres = SStotal- SSreg = 66 - 19.5 = 46.5.
MSres = SSres/dfres = 46.5/30 = 1.55
F = MSreg/MSres = 6.5/1.55 = 4.19; critical value = .05F3,30 = 2.92 < F, reject H0.

4
You are given the following data, where X1 (attendance rate) and X2 (average SAT score) are to be used to predict Y (average score in graduation test). Each case represents one school.
Determine the following values: intercept, b1, b2, SSres, SSreg, F, sres2, s(b1), s(b2), t1, t2.
Determine the following values: intercept, b1, b2, SSres, SSreg, F, sres2, s(b1), s(b2), t1, t2.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
5
For the regression model, Yi = b1X1i + b2X2i + a + ei, consider the following two situations:
Situation 1: rY1 = ?0.5 rY2 = 0.8 r12 = 0.1
Situation 2: rY1 = 0.2 rY2 = 0.8 r12 = 0.1
In which of the two situations will R2 be larger?
A) Situation 1.
B) Situation 2.
C) R2 will be the same in both situations.
D) Uncertain.
Situation 1: rY1 = ?0.5 rY2 = 0.8 r12 = 0.1
Situation 2: rY1 = 0.2 rY2 = 0.8 r12 = 0.1
In which of the two situations will R2 be larger?
A) Situation 1.
B) Situation 2.
C) R2 will be the same in both situations.
D) Uncertain.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
6
The scatterplot of X and Y are shown as follows.
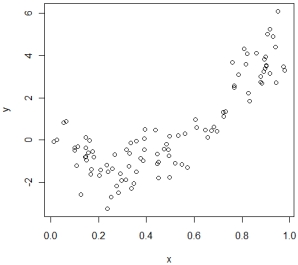 Based on the plot, which model is the most appropriate to use?
Based on the plot, which model is the most appropriate to use?
A) Yi = b1Xi + a + ei.
B) Yi = b1Xi + b2Xi2 + a + ei.
C) Yi = b1Xi2 + a + ei.
D) Yi = b1Xi + b2Xi + b3Xi3 + a + ei.
 Based on the plot, which model is the most appropriate to use?
Based on the plot, which model is the most appropriate to use?A) Yi = b1Xi + a + ei.
B) Yi = b1Xi + b2Xi2 + a + ei.
C) Yi = b1Xi2 + a + ei.
D) Yi = b1Xi + b2Xi + b3Xi3 + a + ei.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following situations will result in the best prediction in multiple regression analysis?
A) rY1 = 0.1 rY2 = 0.4 r12 = 0.1
B) rY1 = 0.1 rY2 = 0.4 r12 = 0.8
C) rY1 = 0.6 rY2 = 0.4 r12 = 0.1
D) rY1 = 0.6 rY2 = 0.4 r12 = 0.8
A) rY1 = 0.1 rY2 = 0.4 r12 = 0.1
B) rY1 = 0.1 rY2 = 0.4 r12 = 0.8
C) rY1 = 0.6 rY2 = 0.4 r12 = 0.1
D) rY1 = 0.6 rY2 = 0.4 r12 = 0.8

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
8
Which one of the following reflects variables appropriate for a multiple linear regression model?
A) One categorical dependent variable and one continuous independent variable
B) One continuous dependent variable and one continuous or categorical independent variable
C) One continuous dependent variable and two or more continuous independent variables
D) Two or more continuous dependent variables and one continuous or categorical independent variable
A) One categorical dependent variable and one continuous independent variable
B) One continuous dependent variable and one continuous or categorical independent variable
C) One continuous dependent variable and two or more continuous independent variables
D) Two or more continuous dependent variables and one continuous or categorical independent variable

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
9
In a multiple linear regression with three independent variables, X1, X2, and X3, which one of the following reflects an example of a semipartial correlation?
A) The correlation between X1 and X2 and X3 where both X2 and X3 are removed from X1 and X2
B) The correlation between X1 and X2 where X3 is held constant
C) The correlation between X2 and X3 where X1 is partialed out
D) The correlation between X1 and X2 where X3 is removed from X2 only
A) The correlation between X1 and X2 and X3 where both X2 and X3 are removed from X1 and X2
B) The correlation between X1 and X2 where X3 is held constant
C) The correlation between X2 and X3 where X1 is partialed out
D) The correlation between X1 and X2 where X3 is removed from X2 only

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
10
Partial correlations allow for which one of the following in multiple linear regression?
A) Design control
B) Experiential control
C) Experimental control
D) Statistical control
A) Design control
B) Experiential control
C) Experimental control
D) Statistical control

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck


