Deck 15: Multiple Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/105
Play
Full screen (f)
Deck 15: Multiple Integration
1
Use the Riemann sum corresponding to a subdivision of the rectangular region R defined by 0 x 6, 0 y 4, into six squares of edge length 2 and sample points at the upper-right corner of each square to estimate 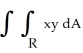 .
.
A) 72
B) 288
C) 144
D) 36
E) 168
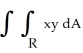 .
.A) 72
B) 288
C) 144
D) 36
E) 168
288
2
Use the Riemann sum corresponding to a subdivision of the rectangular region R defined by 0 x 6, 0 y 4, into six squares of edge length 2 and sample points at the centre of each square to estimate 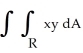 .
.
A) 72
B) 288
C) 144
D) 36
E) 120
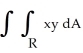 .
.A) 72
B) 288
C) 144
D) 36
E) 120
144
3
Evaluate 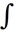
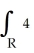 dA, where R is the rectangle 6 x 9, -3 y 2, by interpreting it as a known volume.
dA, where R is the rectangle 6 x 9, -3 y 2, by interpreting it as a known volume.
A) 4
B) 15
C) 72
D) 60
E) 12
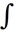
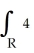 dA, where R is the rectangle 6 x 9, -3 y 2, by interpreting it as a known volume.
dA, where R is the rectangle 6 x 9, -3 y 2, by interpreting it as a known volume.A) 4
B) 15
C) 72
D) 60
E) 12
60
4
Evaluate 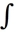
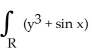 dA, where R is the square -2 x 2, -2 y 2.
dA, where R is the square -2 x 2, -2 y 2.
A) 0
B) 2
C)
D) 17.68
E) 2
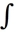
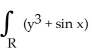 dA, where R is the square -2 x 2, -2 y 2.
dA, where R is the square -2 x 2, -2 y 2.A) 0
B) 2
C)
D) 17.68
E) 2

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate 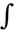
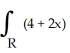 dA, where R is the rectangle -2 x 2, -3 y 3, by interpreting it as a known volume.
dA, where R is the rectangle -2 x 2, -3 y 3, by interpreting it as a known volume.
A) 144
B) 48
C) 96
D) 24
E) 0
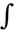
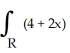 dA, where R is the rectangle -2 x 2, -3 y 3, by interpreting it as a known volume.
dA, where R is the rectangle -2 x 2, -3 y 3, by interpreting it as a known volume.A) 144
B) 48
C) 96
D) 24
E) 0

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate 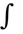
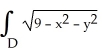 dA, where D is the disk
dA, where D is the disk 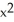 +
+ 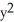 9, by interpreting it as a known volume.X
9, by interpreting it as a known volume.X
A) 12
B) 18
C) 24
D) 36
E) 9
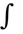
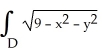 dA, where D is the disk
dA, where D is the disk 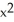 +
+ 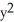 9, by interpreting it as a known volume.X
9, by interpreting it as a known volume.XA) 12
B) 18
C) 24
D) 36
E) 9

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate 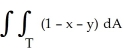 , where T is the triangle in the xy-plane bounded by the coordinate axes and the line x + y = 1, by interpreting the double integral as a known volume.
, where T is the triangle in the xy-plane bounded by the coordinate axes and the line x + y = 1, by interpreting the double integral as a known volume.
A)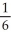
B)
C)
D)
E)
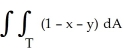 , where T is the triangle in the xy-plane bounded by the coordinate axes and the line x + y = 1, by interpreting the double integral as a known volume.
, where T is the triangle in the xy-plane bounded by the coordinate axes and the line x + y = 1, by interpreting the double integral as a known volume.A)
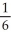
B)

C)

D)

E)


Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate 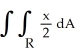 , where R is the rectangle 0 x 5, 2 y 10, by interpreting the double integral as a known volume.
, where R is the rectangle 0 x 5, 2 y 10, by interpreting the double integral as a known volume.
A) 25
B) 50
C) 75
D) 100
E) 20
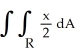 , where R is the rectangle 0 x 5, 2 y 10, by interpreting the double integral as a known volume.
, where R is the rectangle 0 x 5, 2 y 10, by interpreting the double integral as a known volume.A) 25
B) 50
C) 75
D) 100
E) 20

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate 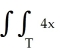 dA over the triangle T with vertices (0, 0), (0, 1), and (1,1).
dA over the triangle T with vertices (0, 0), (0, 1), and (1,1).
A)
B)
C)
D)
E)
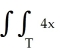 dA over the triangle T with vertices (0, 0), (0, 1), and (1,1).
dA over the triangle T with vertices (0, 0), (0, 1), and (1,1).A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate 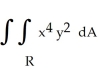 over the rectangle -1 x 2, 0 y 3.
over the rectangle -1 x 2, 0 y 3.
A)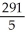
B)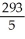
C)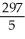
D)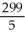
E) 59
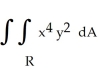 over the rectangle -1 x 2, 0 y 3.
over the rectangle -1 x 2, 0 y 3.A)
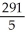
B)
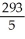
C)
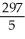
D)
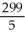
E) 59

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate the double integral 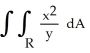 over the rectangle R bounded by the lines x = 0, x = 2, y = 1, and y = 2.
over the rectangle R bounded by the lines x = 0, x = 2, y = 1, and y = 2.
A)
B)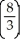 ln 2
ln 2
C)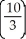 ln 2
ln 2
D)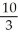
E) 2
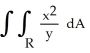 over the rectangle R bounded by the lines x = 0, x = 2, y = 1, and y = 2.
over the rectangle R bounded by the lines x = 0, x = 2, y = 1, and y = 2.A)

B)
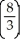 ln 2
ln 2C)
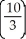 ln 2
ln 2D)
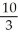
E) 2

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate 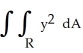 , where R is the region bounded by y = 2x, y = 5x, and x = 2.
, where R is the region bounded by y = 2x, y = 5x, and x = 2.
A) 144
B) 156
C) 160
D) 172
E) 184
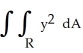 , where R is the region bounded by y = 2x, y = 5x, and x = 2.
, where R is the region bounded by y = 2x, y = 5x, and x = 2.A) 144
B) 156
C) 160
D) 172
E) 184

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate 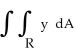 , where R is the bounded region bounded by y = x and y = x2.
, where R is the bounded region bounded by y = x and y = x2.
A)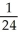
B)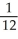
C)
D)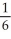
E)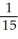
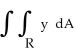 , where R is the bounded region bounded by y = x and y = x2.
, where R is the bounded region bounded by y = x and y = x2.A)
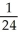
B)
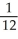
C)

D)
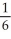
E)
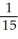

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate 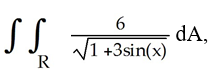 where R is the planar region described by 0 ≤ x ≤
where R is the planar region described by 0 ≤ x ≤ 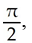 0 ≤ y ≤ cos(x).
0 ≤ y ≤ cos(x).
A) 4
B) 12
C) 0
D) - 3
E) 8
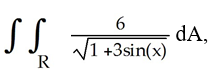 where R is the planar region described by 0 ≤ x ≤
where R is the planar region described by 0 ≤ x ≤ 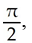 0 ≤ y ≤ cos(x).
0 ≤ y ≤ cos(x). A) 4
B) 12
C) 0
D) - 3
E) 8

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the double integral 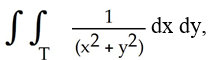 where T is the quadrilateral bounded by the lines x = 1, x = 2, y = x, and y =
where T is the quadrilateral bounded by the lines x = 1, x = 2, y = x, and y = 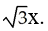
A)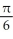 ln 2
ln 2
B)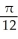 ln 2
ln 2
C)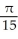 ln 2
ln 2
D)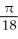 ln 2
ln 2
E)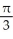 ln 2
ln 2
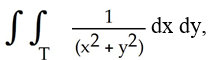 where T is the quadrilateral bounded by the lines x = 1, x = 2, y = x, and y =
where T is the quadrilateral bounded by the lines x = 1, x = 2, y = x, and y = 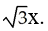
A)
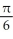 ln 2
ln 2B)
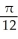 ln 2
ln 2C)
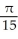 ln 2
ln 2D)
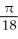 ln 2
ln 2E)
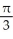 ln 2
ln 2
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the iterated integral 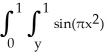 dx dy by first reiterating it in the opposite direction.
dx dy by first reiterating it in the opposite direction.
A)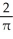
B)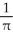
C)
D)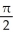
E)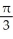
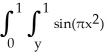 dx dy by first reiterating it in the opposite direction.
dx dy by first reiterating it in the opposite direction.A)
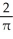
B)
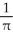
C)
D)
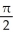
E)
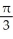

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate 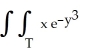 dA, where T is the triangle with vertices (0, 0), (0, 2), and (2, 2).
dA, where T is the triangle with vertices (0, 0), (0, 2), and (2, 2).
A) -
- 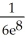
B)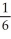 -
- 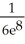
C) -
- 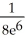
D)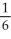 -
- 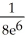
E)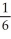 +
+ 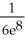
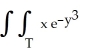 dA, where T is the triangle with vertices (0, 0), (0, 2), and (2, 2).
dA, where T is the triangle with vertices (0, 0), (0, 2), and (2, 2).A)
 -
- 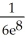
B)
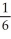 -
- 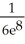
C)
 -
- 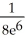
D)
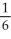 -
- 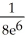
E)
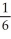 +
+ 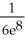

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate 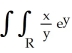 dA, where R is the region defined by the inequalities x2 y x.
dA, where R is the region defined by the inequalities x2 y x.
A) - 1
- 1
B) 1 -
C)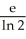
D)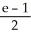
E) e -
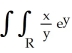 dA, where R is the region defined by the inequalities x2 y x.
dA, where R is the region defined by the inequalities x2 y x.A)
 - 1
- 1B) 1 -

C)
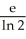
D)
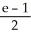
E) e -


Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
19
Find the volume of the solid bounded above by the paraboloid z = 9x2 + y2, below by the plane 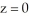 , and laterally by the planes x = 0, y = 0, x = 3, and y = 2.
, and laterally by the planes x = 0, y = 0, x = 3, and y = 2.
A) 170 cubic units
B) 180 cubic units
C) 190 cubic units
D) 200 cubic units
E) 90 cubic units
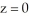 , and laterally by the planes x = 0, y = 0, x = 3, and y = 2.
, and laterally by the planes x = 0, y = 0, x = 3, and y = 2.A) 170 cubic units
B) 180 cubic units
C) 190 cubic units
D) 200 cubic units
E) 90 cubic units

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate 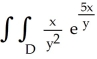 dA, where D is the rectangular region described by the inequalities 0 x 10 ln(13), 25 y 50.
dA, where D is the rectangular region described by the inequalities 0 x 10 ln(13), 25 y 50.
A) 144
B) 1
C)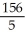
D) 143
E)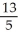
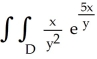 dA, where D is the rectangular region described by the inequalities 0 x 10 ln(13), 25 y 50.
dA, where D is the rectangular region described by the inequalities 0 x 10 ln(13), 25 y 50.A) 144
B) 1
C)
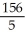
D) 143
E)
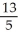

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
21
Find the volume of the solid in the first octant inside the cylinder x2 + y2 = 2y and under the plane z = 2 - x.
A)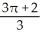 cubic units
cubic units
B)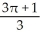 cubic units
cubic units
C)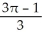 cubic units
cubic units
D)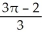 cubic units
cubic units
E)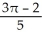 cubic units
cubic units
A)
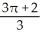 cubic units
cubic unitsB)
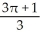 cubic units
cubic unitsC)
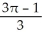 cubic units
cubic unitsD)
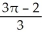 cubic units
cubic unitsE)
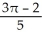 cubic units
cubic units
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate the iterated integral 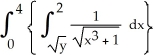 dy by first reversing the order of the integration.
dy by first reversing the order of the integration.
A)
B) 4
C)
D) 2
E)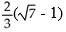
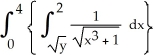 dy by first reversing the order of the integration.
dy by first reversing the order of the integration.A)

B) 4
C)

D) 2
E)
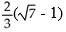

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
23
Find the volume of the solid lying inside the cylinder x2 + y2 = 4, above the plane z = x - y - 8, and below the surface z = 8 - x3.
A) 72 cubic units
B) 64 cubic units
C) 48 cubic units
D) 32 cubic units
E) 56 cubic units
A) 72 cubic units
B) 64 cubic units
C) 48 cubic units
D) 32 cubic units
E) 56 cubic units

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate 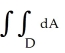 where D is the region in the xy-plane enclosed by the parallelogram with vertices at the points (2, 4), (4, 9), (10, 9), and (8, 4).
where D is the region in the xy-plane enclosed by the parallelogram with vertices at the points (2, 4), (4, 9), (10, 9), and (8, 4).
A) 12
B) 15
C) 0
D) 6
E) 30
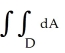 where D is the region in the xy-plane enclosed by the parallelogram with vertices at the points (2, 4), (4, 9), (10, 9), and (8, 4).
where D is the region in the xy-plane enclosed by the parallelogram with vertices at the points (2, 4), (4, 9), (10, 9), and (8, 4).A) 12
B) 15
C) 0
D) 6
E) 30

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
25
Find the volume of the solid below the surface z = 3y2 and above the triangular region in the xy-plane bounded by the straight lines x = 0, y = 0, and x + 2y = 2.
A) 6
B) 2
C)
D) 12
E)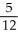
A) 6
B) 2
C)

D) 12
E)
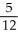

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
26
The iterated integral 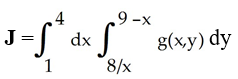 is the double integral of g(x,y) over a planar region R.
is the double integral of g(x,y) over a planar region R.
(i) Sketch the planar region R.
(ii) Express the double integral J as a sum of two iterated integrals with the order of the integrals reversed.
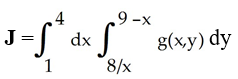 is the double integral of g(x,y) over a planar region R.
is the double integral of g(x,y) over a planar region R.(i) Sketch the planar region R.
(ii) Express the double integral J as a sum of two iterated integrals with the order of the integrals reversed.

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
27
Find the volume of the solid bounded by the paraboloid z = 16 - x2 - 4y2 and the planez = 0.
A) 48 cubic units
B) 64 cubic units
C) 96 cubic units
D) 128 cubic units
E) 81 cubic units
A) 48 cubic units
B) 64 cubic units
C) 96 cubic units
D) 128 cubic units
E) 81 cubic units

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
28
The planar region enclosed by the straight lines y = x, y = 1 + x, y = -x, and y = 1 -x is both x-simple and y-simple.

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the double integral 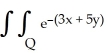 dx dy, where Q is the first quadrant of the xy-plane.
dx dy, where Q is the first quadrant of the xy-plane.
A)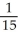
B) 15
C) 1
D) (integral diverges)
E) -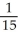
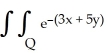 dx dy, where Q is the first quadrant of the xy-plane.
dx dy, where Q is the first quadrant of the xy-plane.A)
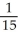
B) 15
C) 1
D) (integral diverges)
E) -
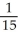

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate the double integral 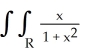 dx dy, where R is the region under the curve xy = 1, above the x-axis, and to the right of the line x = 1.
dx dy, where R is the region under the curve xy = 1, above the x-axis, and to the right of the line x = 1.
A)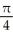
B)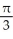
C)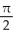
D) (integral diverges)
E)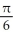
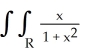 dx dy, where R is the region under the curve xy = 1, above the x-axis, and to the right of the line x = 1.
dx dy, where R is the region under the curve xy = 1, above the x-axis, and to the right of the line x = 1.A)
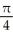
B)
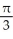
C)
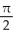
D) (integral diverges)
E)
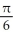

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the double integral 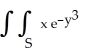 dx dy, where S is the part of the first quadrant of the xy-plane lying above the line x = 2y.
dx dy, where S is the part of the first quadrant of the xy-plane lying above the line x = 2y.
A)
B)
C)
D) (integral diverges)
E) 1
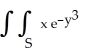 dx dy, where S is the part of the first quadrant of the xy-plane lying above the line x = 2y.
dx dy, where S is the part of the first quadrant of the xy-plane lying above the line x = 2y.A)

B)

C)

D) (integral diverges)
E) 1

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate 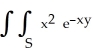 dx dy, where S is the semi-infinite strip 0 x 1, 0 y < .
dx dy, where S is the semi-infinite strip 0 x 1, 0 y < .
A) 1
B)
C)
D) (integral diverges)
E) 2
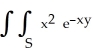 dx dy, where S is the semi-infinite strip 0 x 1, 0 y < .
dx dy, where S is the semi-infinite strip 0 x 1, 0 y < .A) 1
B)

C)

D) (integral diverges)
E) 2

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate 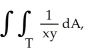 where T is the triangle with vertices (0, 0), (1, 1), and (1, 2).
where T is the triangle with vertices (0, 0), (1, 1), and (1, 2).
A) ln(2)
B) 2 ln(2)
C) 2
D) (integral diverges)
E)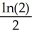
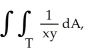 where T is the triangle with vertices (0, 0), (1, 1), and (1, 2).
where T is the triangle with vertices (0, 0), (1, 1), and (1, 2).A) ln(2)
B) 2 ln(2)
C) 2
D) (integral diverges)
E)
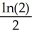

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate 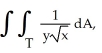 where T is the triangle with vertices (0, 0), (1, 1), and (1, 2).
where T is the triangle with vertices (0, 0), (1, 1), and (1, 2).
A) ln(2)
B) 2 ln(2)
C) 2
D) (integral diverges)
E)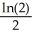
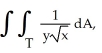 where T is the triangle with vertices (0, 0), (1, 1), and (1, 2).
where T is the triangle with vertices (0, 0), (1, 1), and (1, 2).A) ln(2)
B) 2 ln(2)
C) 2
D) (integral diverges)
E)
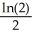

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
35
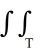
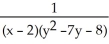 dA, where T is the triangular region enclosed by the straight lines y = -x, y = 7x, and y = x + 6 is an improper integral.
dA, where T is the triangular region enclosed by the straight lines y = -x, y = 7x, and y = x + 6 is an improper integral.
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
36
The improper double integral 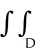
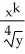 dA, where D is the planar region described by1 x < , 0 y x8, converges for all real numbers k such that
dA, where D is the planar region described by1 x < , 0 y x8, converges for all real numbers k such that
A) k - 7
B) k > 5
C) k < 9
D) k <- 7
E) k 5
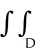
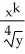 dA, where D is the planar region described by1 x < , 0 y x8, converges for all real numbers k such that
dA, where D is the planar region described by1 x < , 0 y x8, converges for all real numbers k such thatA) k - 7
B) k > 5
C) k < 9
D) k <- 7
E) k 5

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
37
Find 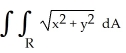 if R is the unit circular disk x2 + y2 9.
if R is the unit circular disk x2 + y2 9.
A) 9
B) 18
C)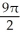
D) 18
E) 9
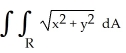 if R is the unit circular disk x2 + y2 9.
if R is the unit circular disk x2 + y2 9.A) 9
B) 18
C)
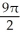
D) 18
E) 9

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
38
Find the average value of x2 + y2 over the disk x2 + y2 4.
A) 2
B)
C)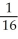
D) 4
E)
A) 2
B)

C)
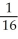
D) 4
E)


Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
39
Find 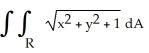 if R is the unit circular disk.
if R is the unit circular disk.
A)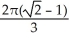
B)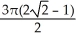
C)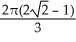
D)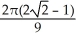
E)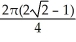
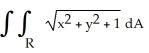 if R is the unit circular disk.
if R is the unit circular disk.A)
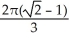
B)
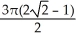
C)
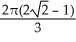
D)
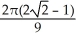
E)
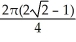

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
40
Find 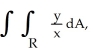 where R is the region in the first quadrant lying between the circles x2 + y2 = 1 and x2 + y2 = 4 and between the lines y = 0 and y = x.
where R is the region in the first quadrant lying between the circles x2 + y2 = 1 and x2 + y2 = 4 and between the lines y = 0 and y = x.
A) ln 2
ln 2
B) ln 2
ln 2
C) ln 2
ln 2
D)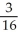 ln 2
ln 2
E) ln 2
ln 2
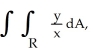 where R is the region in the first quadrant lying between the circles x2 + y2 = 1 and x2 + y2 = 4 and between the lines y = 0 and y = x.
where R is the region in the first quadrant lying between the circles x2 + y2 = 1 and x2 + y2 = 4 and between the lines y = 0 and y = x.A)
 ln 2
ln 2B)
 ln 2
ln 2C)
 ln 2
ln 2D)
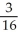 ln 2
ln 2E)
 ln 2
ln 2
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
41
Find the volume of the given solid by transforming to a double integral in polar coordinates.The solid is bounded by x2 + y2 = 36, z = 0, and z = x2 + y2.
A) 618 cubic units
B) 628 cubic units
C) 638 cubic units
D) 648 cubic units
E) 658 cubic units
A) 618 cubic units
B) 628 cubic units
C) 638 cubic units
D) 648 cubic units
E) 658 cubic units

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
42
Use polar coordinates to find the volume of the solid lying under the cone z = 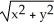 , above the plane z = 0, and inside the cylinder x2 + y2 = 2x.
, above the plane z = 0, and inside the cylinder x2 + y2 = 2x.
A)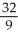 cubic units
cubic units
B)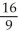 cubic units
cubic units
C)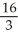 cubic units
cubic units
D) cubic units
cubic units
E) cubic units
cubic units
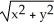 , above the plane z = 0, and inside the cylinder x2 + y2 = 2x.
, above the plane z = 0, and inside the cylinder x2 + y2 = 2x.A)
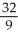 cubic units
cubic units B)
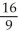 cubic units
cubic units C)
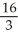 cubic units
cubic units D)
 cubic units
cubic units E)
 cubic units
cubic units 
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
43
Find the volume remaining after a cylindrical hole of radius b is drilled through the centre of a ball of radius a > b.
A) a
a 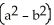 cubic units
cubic units
B)
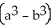 cubic units
cubic units
C)
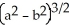 cubic units
cubic units
D)
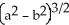 cubic units
cubic units
E)
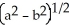 cubic units
cubic units
A)
 a
a 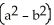 cubic units
cubic unitsB)

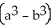 cubic units
cubic unitsC)

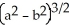 cubic units
cubic unitsD)

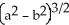 cubic units
cubic unitsE)

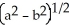 cubic units
cubic units
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
44
Use polar coordinates to evaluate 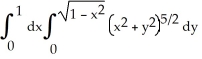 .
.
A)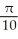
B)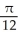
C)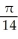
D)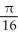
E)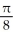
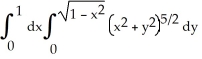 .
.A)
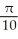
B)
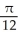
C)
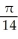
D)
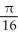
E)
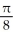

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
45
Expressed in polar coordinates, the area enclosed by a planar region D is equal to 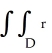 dr d .
dr d .
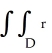 dr d .
dr d . 
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
46
Find 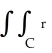 dA, where C is the cardioid disk 0 r 1 + cos .
dA, where C is the cardioid disk 0 r 1 + cos .
A)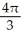
B)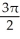
C)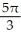
D)
E)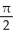
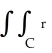 dA, where C is the cardioid disk 0 r 1 + cos .
dA, where C is the cardioid disk 0 r 1 + cos .A)
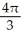
B)
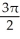
C)
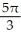
D)
E)
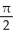

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
47
Find the volume of the solid of revolution obtained by rotating the plane region bounded by the cardioid r = 1 + sin about the y-axis.
A)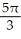 cubic units
cubic units
B)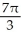 cubic units
cubic units
C)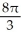 cubic units
cubic units
D)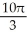 cubic units
cubic units
E)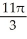
A)
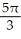 cubic units
cubic unitsB)
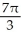 cubic units
cubic unitsC)
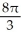 cubic units
cubic unitsD)
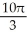 cubic units
cubic unitsE)
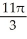

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate the iterated integral 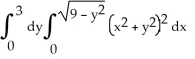 by first transforming it to an iterated integral in polar coordinates.
by first transforming it to an iterated integral in polar coordinates.
A)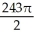
B)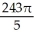
C)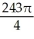
D)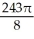
E) 243
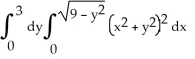 by first transforming it to an iterated integral in polar coordinates.
by first transforming it to an iterated integral in polar coordinates.A)
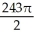
B)
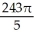
C)
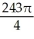
D)
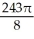
E) 243

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate the integral 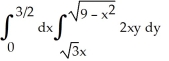 using polar coordinates.
using polar coordinates.
A)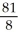
B)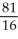
C)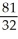
D)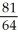
E)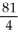
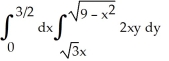 using polar coordinates.
using polar coordinates.A)
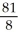
B)
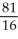
C)
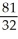
D)
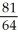
E)
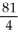

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
50
Find 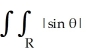 dA, where R is the region outside the circle r = 1 and inside the cardioid r = 1 + cos .
dA, where R is the region outside the circle r = 1 and inside the cardioid r = 1 + cos .
A)
B)
C)
D)
E)
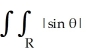 dA, where R is the region outside the circle r = 1 and inside the cardioid r = 1 + cos .
dA, where R is the region outside the circle r = 1 and inside the cardioid r = 1 + cos .A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
51
If I = 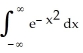 , then I =
, then I = 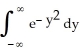 , and so
, and so 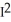 =
= 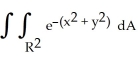 , where R2 is the entire xy-plane. Evaluate this double integral by iterating it in polar coordinates and hence find the value of I.
, where R2 is the entire xy-plane. Evaluate this double integral by iterating it in polar coordinates and hence find the value of I.
A) I =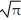
B) I =
C) I =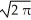
D) I =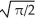
E) I = 2
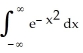 , then I =
, then I = 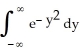 , and so
, and so 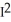 =
= 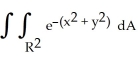 , where R2 is the entire xy-plane. Evaluate this double integral by iterating it in polar coordinates and hence find the value of I.
, where R2 is the entire xy-plane. Evaluate this double integral by iterating it in polar coordinates and hence find the value of I.A) I =
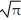
B) I =
C) I =
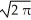
D) I =
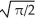
E) I = 2

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
52
Use polar coordinates to find the volume of the solid enclosed by the surfaces z = 3 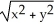 and
and 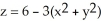 .
.
A) 16
B)
C) 4
D) 8
E) 7
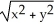 and
and 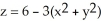 .
.A) 16
B)

C) 4
D) 8
E) 7

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
53
Let R be the region in the first quadrant of the xy-plane bounded by the curves xy = 1 and xy = 4 and the lines y = x and y = 2x. Use a suitable coordinate transformation to evaluate 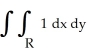 and hence find the area of R.
and hence find the area of R.
A) 8 square units
B) 4 ln(3) square units
C) 5 ln(3) square units
D) 3 ln(2) square units
E) 16 square units
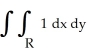 and hence find the area of R.
and hence find the area of R.A) 8 square units
B) 4 ln(3) square units
C) 5 ln(3) square units
D) 3 ln(2) square units
E) 16 square units

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
54
Use a suitable change of variables to evaluate 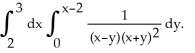
A)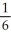 (1 + ln(2))
(1 + ln(2))
B)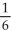 (1 - ln(2))
(1 - ln(2))
C)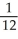 (1 + ln(2))
(1 + ln(2))
D)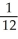 (1 - ln(2))
(1 - ln(2))
E)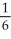 ln(2)
ln(2)
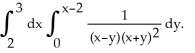
A)
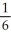 (1 + ln(2))
(1 + ln(2))B)
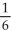 (1 - ln(2))
(1 - ln(2))C)
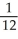 (1 + ln(2))
(1 + ln(2))D)
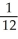 (1 - ln(2))
(1 - ln(2))E)
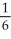 ln(2)
ln(2)
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
55
Use the transformation u = x + y, v = 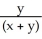 to evaluate the double integral of f(x, y) =
to evaluate the double integral of f(x, y) = 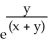 over the triangular region bounded by the lines x + y = 1, x = 0, and y = 0.
over the triangular region bounded by the lines x + y = 1, x = 0, and y = 0.
A)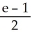
B)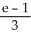
C)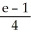
D)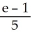
E)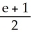
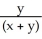 to evaluate the double integral of f(x, y) =
to evaluate the double integral of f(x, y) = 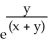 over the triangular region bounded by the lines x + y = 1, x = 0, and y = 0.
over the triangular region bounded by the lines x + y = 1, x = 0, and y = 0.A)
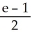
B)
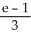
C)
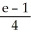
D)
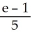
E)
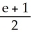

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
56
Evaluate 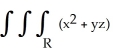 dV, where R is the rectangular box 0 x 1, 1 y 2, 1 z 2.
dV, where R is the rectangular box 0 x 1, 1 y 2, 1 z 2.
A)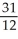
B)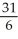
C)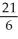
D)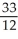
E)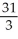
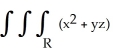 dV, where R is the rectangular box 0 x 1, 1 y 2, 1 z 2.
dV, where R is the rectangular box 0 x 1, 1 y 2, 1 z 2.A)
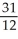
B)
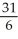
C)
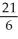
D)
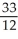
E)
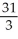

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
57
Compute the integral 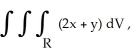 where R is the tetrahedral region bounded by the planes x = 0, y = 0, z = 0, and x + y + z = 4.
where R is the tetrahedral region bounded by the planes x = 0, y = 0, z = 0, and x + y + z = 4.
A) 16
B) 8
C) 32
D) 24
E)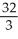
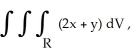 where R is the tetrahedral region bounded by the planes x = 0, y = 0, z = 0, and x + y + z = 4.
where R is the tetrahedral region bounded by the planes x = 0, y = 0, z = 0, and x + y + z = 4.A) 16
B) 8
C) 32
D) 24
E)
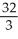

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the integral 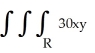 dV, where R is the region defined by the inequalities0 y 1, 0 z y, 0 x z.
dV, where R is the region defined by the inequalities0 y 1, 0 z y, 0 x z.
A)
B) 2
C)
D)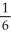
E) 1
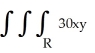 dV, where R is the region defined by the inequalities0 y 1, 0 z y, 0 x z.
dV, where R is the region defined by the inequalities0 y 1, 0 z y, 0 x z.A)

B) 2
C)

D)
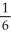
E) 1

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the integral 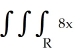 dV, where R is the region in the first octant bounded by the four planes x = 1, y = x, z = 0, and z = y.
dV, where R is the region in the first octant bounded by the four planes x = 1, y = x, z = 0, and z = y.
A) 3
B) 2
C) 1
D) 4
E) 5
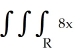 dV, where R is the region in the first octant bounded by the four planes x = 1, y = x, z = 0, and z = y.
dV, where R is the region in the first octant bounded by the four planes x = 1, y = x, z = 0, and z = y.A) 3
B) 2
C) 1
D) 4
E) 5

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
60
Evaluate the triple integral over the region 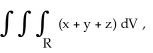 where R is the finite region bounded by z = 0, y + z = 4, y = x2.
where R is the finite region bounded by z = 0, y + z = 4, y = x2.
A)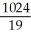
B)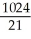
C)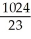
D)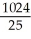
E)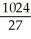
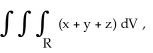 where R is the finite region bounded by z = 0, y + z = 4, y = x2.
where R is the finite region bounded by z = 0, y + z = 4, y = x2.A)
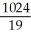
B)
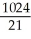
C)
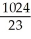
D)
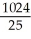
E)

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
61
Express the iterated integral 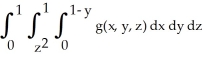 as an equivalent integral in which the outermost integral is with respect to x and the innermost is with respect to y.
as an equivalent integral in which the outermost integral is with respect to x and the innermost is with respect to y.
A)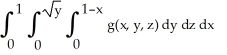
B)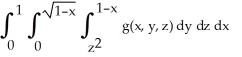
C)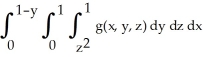
D)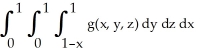
E)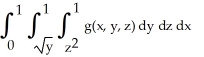
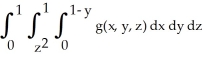 as an equivalent integral in which the outermost integral is with respect to x and the innermost is with respect to y.
as an equivalent integral in which the outermost integral is with respect to x and the innermost is with respect to y.A)
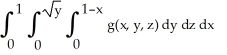
B)
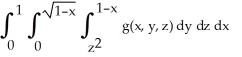
C)
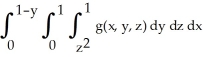
D)
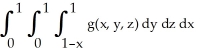
E)
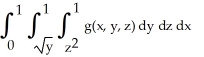

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate 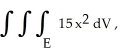 where E is the region in 3-space described by the inequalities0 ≤ x ≤ 2 - y - z, 0 ≤ z ≤ 2 - y, and 0 ≤ y ≤ 2.
where E is the region in 3-space described by the inequalities0 ≤ x ≤ 2 - y - z, 0 ≤ z ≤ 2 - y, and 0 ≤ y ≤ 2.
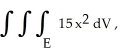 where E is the region in 3-space described by the inequalities0 ≤ x ≤ 2 - y - z, 0 ≤ z ≤ 2 - y, and 0 ≤ y ≤ 2.
where E is the region in 3-space described by the inequalities0 ≤ x ≤ 2 - y - z, 0 ≤ z ≤ 2 - y, and 0 ≤ y ≤ 2.
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate 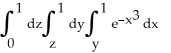 by completely reversing the order in which the integrals are performed.
by completely reversing the order in which the integrals are performed.
A)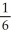 +
+ 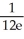
B)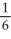 -
- 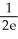
C)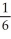 +
+ 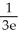
D)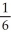 -
- 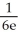
E)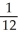 -
- 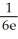
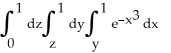 by completely reversing the order in which the integrals are performed.
by completely reversing the order in which the integrals are performed.A)
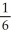 +
+ 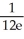
B)
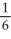 -
- 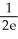
C)
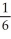 +
+ 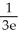
D)
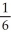 -
- 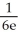
E)
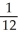 -
- 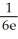

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
64
Find the volume of the solid that lies below the surface z = 1 + 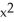 and above the region in the xy-plane bounded by the straight lines y = -x, y = x, and y = 1.
and above the region in the xy-plane bounded by the straight lines y = -x, y = x, and y = 1.
A) V =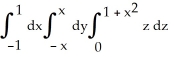
B) V =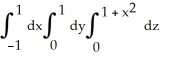
C) V =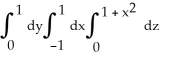
D) V =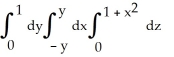
E) V =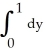
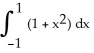
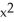 and above the region in the xy-plane bounded by the straight lines y = -x, y = x, and y = 1.
and above the region in the xy-plane bounded by the straight lines y = -x, y = x, and y = 1.A) V =
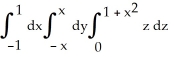
B) V =
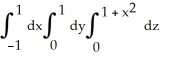
C) V =
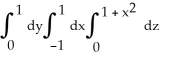
D) V =
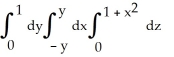
E) V =
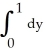
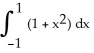

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
65
Use a triple integral to find the volume V of the solid inside the cylinder x2 + y2 = 16 and between the planes z = x - y - 2 and z = 6 + x - y.
A) 64 cubic units
B) 32 cubic units
C) 128 cubic units
D) 256 cubic units
E) 144 cubic units
A) 64 cubic units
B) 32 cubic units
C) 128 cubic units
D) 256 cubic units
E) 144 cubic units

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate the iterated integral 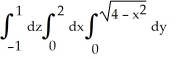 by transforming it to cylindrical coordinates.
by transforming it to cylindrical coordinates.
A) 5
B) 4
C) 3
D) 2
E)
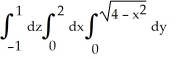 by transforming it to cylindrical coordinates.
by transforming it to cylindrical coordinates.A) 5
B) 4
C) 3
D) 2
E)

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate 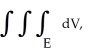 where E is the region in space enclosed by the sphere(x - 1)2 + y2 + z2 = 3.
where E is the region in space enclosed by the sphere(x - 1)2 + y2 + z2 = 3.
A) 9
B) 12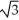
C) 27
D) 36
E) 4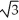
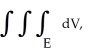 where E is the region in space enclosed by the sphere(x - 1)2 + y2 + z2 = 3.
where E is the region in space enclosed by the sphere(x - 1)2 + y2 + z2 = 3.A) 9
B) 12
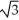
C) 27
D) 36
E) 4
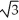

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate the triple integral 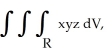 where R is the first octant region abovez = x2 + y2 and below
where R is the first octant region abovez = x2 + y2 and below 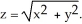
A)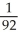
B)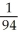
C)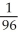
D)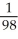
E)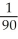
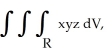 where R is the first octant region abovez = x2 + y2 and below
where R is the first octant region abovez = x2 + y2 and below 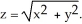
A)
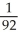
B)
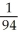
C)
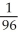
D)
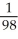
E)

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
69
Use a triple integral iterated in spherical coordinates to find the volume of the region lying above the cone 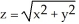 and inside the sphere x2 + y2 + z2 = a2.
and inside the sphere x2 + y2 + z2 = a2.
A)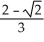
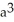 cubic units
cubic units
B)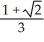
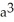 cubic units
cubic units
C)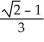
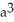 cubic units
cubic units
D)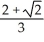
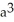 cubic units
cubic units
E)
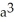 cubic units
cubic units
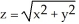 and inside the sphere x2 + y2 + z2 = a2.
and inside the sphere x2 + y2 + z2 = a2.A)
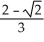
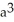 cubic units
cubic unitsB)
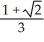
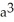 cubic units
cubic unitsC)
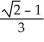
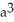 cubic units
cubic unitsD)
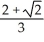
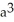 cubic units
cubic unitsE)

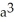 cubic units
cubic units
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate 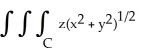 dV, where C is the right circular cylinder consisting of all points (x, y, z) satisfying x2 + y2 3 and -1 z 2.
dV, where C is the right circular cylinder consisting of all points (x, y, z) satisfying x2 + y2 3 and -1 z 2.
A) 33/2
B) 3-(3/2)
C) 35/2
D) 33/2
E) 27
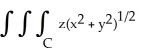 dV, where C is the right circular cylinder consisting of all points (x, y, z) satisfying x2 + y2 3 and -1 z 2.
dV, where C is the right circular cylinder consisting of all points (x, y, z) satisfying x2 + y2 3 and -1 z 2.A) 33/2
B) 3-(3/2)
C) 35/2
D) 33/2
E) 27

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
71
The plane x + y + z = 1 slices the ball x2 + y2 + z2 1 into two pieces. Find the volume of the smaller piece. (Hint: Replace the plane by a horizontal plane at the same distance from the origin.)
A)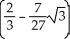 cubic units
cubic units
B)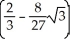 cubic units
cubic units
C)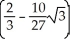 cubic units
cubic units
D)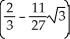 cubic units
cubic units
E)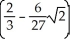 cubic units
cubic units
A)
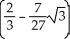 cubic units
cubic unitsB)
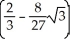 cubic units
cubic unitsC)
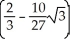 cubic units
cubic unitsD)
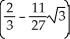 cubic units
cubic unitsE)
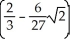 cubic units
cubic units
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
72
Use the transformation x = au, y = bv, z = cw (where a, b, c are positive constants) to evaluate the triple integral of z over the first-octant region bounded by the coordinate planes and the ellipsoid 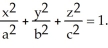
A)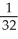
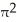
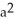
B)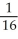
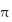
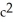
C)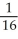
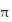 a
a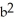 c
c
D)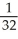
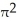
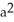 bc
bc
E)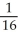 ab
ab 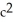
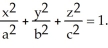
A)
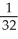
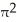
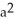
B)
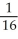
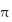
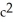
C)
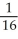
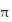 a
a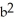 c
cD)
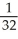
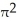
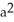 bc
bcE)
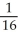 ab
ab 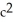

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate the iterated integral 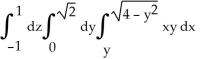 by transforming it to cylindrical coordinates.
by transforming it to cylindrical coordinates.
A) 2
B) 2
C)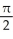
D)
E) 0
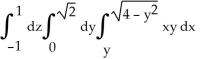 by transforming it to cylindrical coordinates.
by transforming it to cylindrical coordinates.A) 2
B) 2
C)
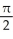
D)

E) 0

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
74
Evaluate 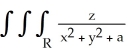 dV, a > 0, where R is the right circular cylinder consisting of all points (x, y, z) satisfying x2 + y2 b, b > 0 and -3 z 5 by using cylindrical coordinates.
dV, a > 0, where R is the right circular cylinder consisting of all points (x, y, z) satisfying x2 + y2 b, b > 0 and -3 z 5 by using cylindrical coordinates.
A) 4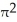 ln
ln 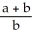
B) 8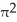 ln
ln 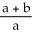
C) 4 ln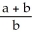
D) 8 ln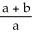
E) 2 ln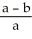
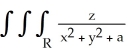 dV, a > 0, where R is the right circular cylinder consisting of all points (x, y, z) satisfying x2 + y2 b, b > 0 and -3 z 5 by using cylindrical coordinates.
dV, a > 0, where R is the right circular cylinder consisting of all points (x, y, z) satisfying x2 + y2 b, b > 0 and -3 z 5 by using cylindrical coordinates.A) 4
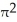 ln
ln 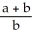
B) 8
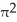 ln
ln 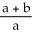
C) 4 ln
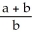
D) 8 ln
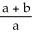
E) 2 ln
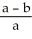

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
75
A solid S has the shape of the region E enclosed by the sphere R = 3cos(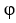 ). Evaluate
). Evaluate 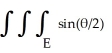 dV .
dV .
Note: R ,11ee7b54_ddf4_a0dd_ae82_79cd253742f9_TB9661_11 , are the spherical coordinates.
A) 12
B) 3
C) 6
D) 9
E)
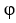 ). Evaluate
). Evaluate 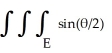 dV .
dV .Note: R ,11ee7b54_ddf4_a0dd_ae82_79cd253742f9_TB9661_11 , are the spherical coordinates.
A) 12
B) 3
C) 6
D) 9
E)


Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
76
Use cylindrical coordinates to compute 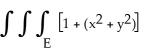 dV where E is the region bounded by the paraboloid z = 6x2 + 4y2 and the cylinder z = 6 - 2y2.
dV where E is the region bounded by the paraboloid z = 6x2 + 4y2 and the cylinder z = 6 - 2y2.
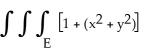 dV where E is the region bounded by the paraboloid z = 6x2 + 4y2 and the cylinder z = 6 - 2y2.
dV where E is the region bounded by the paraboloid z = 6x2 + 4y2 and the cylinder z = 6 - 2y2.
Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate 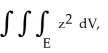 where E is the region enclosed by the ellipsoid
where E is the region enclosed by the ellipsoid 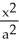 +
+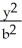 +
+ 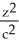 = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw.
= 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw.
A)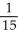 ab
ab 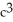
B) ab
ab 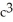
C)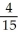 ab
ab 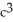
D) ab
ab 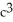
E) ab
ab 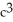
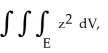 where E is the region enclosed by the ellipsoid
where E is the region enclosed by the ellipsoid  +
+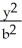 +
+ 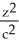 = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw.
= 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw.A)
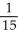 ab
ab 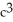
B)
 ab
ab 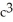
C)
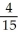 ab
ab 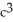
D)
 ab
ab 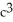
E)
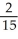 ab
ab 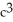

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
78
Let J = ![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_883d_a0f8_e34ffec13eb7_TB9661_11.jpg) where E is the region enclosed by the paraboloids z = 2(
where E is the region enclosed by the paraboloids z = 2( ![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_883e_a0f8_015368bb5f50_TB9661_11.jpg) +
+ ![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_883f_a0f8_71c32f41917f_TB9661_11.jpg) ) and
) and ![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8840_a0f8_bf989c02fab9_TB9661_11.jpg) . Express J in cylindrical coordinates [r, , z]. Do not evaluate.
. Express J in cylindrical coordinates [r, , z]. Do not evaluate.
A)![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8841_a0f8_63ebb4a2c43d_TB9661_11.jpg)
B)![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8842_a0f8_b58e9615aec0_TB9661_11.jpg)
C)![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8843_a0f8_5dcdbb65d6c6_TB9661_11.jpg)
D)![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8844_a0f8_53352620bb66_TB9661_11.jpg)
E)![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8845_a0f8_8ddb9a6cfc0e_TB9661_11.jpg)
![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_883d_a0f8_e34ffec13eb7_TB9661_11.jpg) where E is the region enclosed by the paraboloids z = 2(
where E is the region enclosed by the paraboloids z = 2( ![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_883e_a0f8_015368bb5f50_TB9661_11.jpg) +
+ ![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_883f_a0f8_71c32f41917f_TB9661_11.jpg) ) and
) and ![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8840_a0f8_bf989c02fab9_TB9661_11.jpg) . Express J in cylindrical coordinates [r, , z]. Do not evaluate.
. Express J in cylindrical coordinates [r, , z]. Do not evaluate.A)
![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8841_a0f8_63ebb4a2c43d_TB9661_11.jpg)
B)
![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8842_a0f8_b58e9615aec0_TB9661_11.jpg)
C)
![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8843_a0f8_5dcdbb65d6c6_TB9661_11.jpg)
D)
![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8844_a0f8_53352620bb66_TB9661_11.jpg)
E)
![<strong>Let J = where E is the region enclosed by the paraboloids z = 2( + ) and . Express J in cylindrical coordinates [r, \theta , z]. Do not evaluate.</strong> A) B) C) D) E)](https://storage.examlex.com/TB9661/11ee77e1_77a9_8845_a0f8_8ddb9a6cfc0e_TB9661_11.jpg)

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate 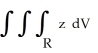 , where R is the region x2 + y2 + z2 4,
, where R is the region x2 + y2 + z2 4, 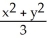 z2 3(x2 + y2), z 0.(Hint: Use spherical coordinates.)
z2 3(x2 + y2), z 0.(Hint: Use spherical coordinates.)
A) 8
B) 2
C) 16
D) 4
E) 32
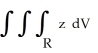 , where R is the region x2 + y2 + z2 4,
, where R is the region x2 + y2 + z2 4, 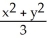 z2 3(x2 + y2), z 0.(Hint: Use spherical coordinates.)
z2 3(x2 + y2), z 0.(Hint: Use spherical coordinates.)A) 8
B) 2
C) 16
D) 4
E) 32

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate 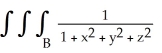 dV, where B is the ball x2 + y2 + z2 a2, a > 0.
dV, where B is the ball x2 + y2 + z2 a2, a > 0.
A) 4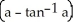
B) 2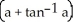
C) 8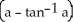
D) 4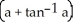
E) 8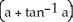
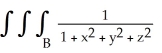 dV, where B is the ball x2 + y2 + z2 a2, a > 0.
dV, where B is the ball x2 + y2 + z2 a2, a > 0.A) 4
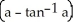
B) 2
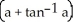
C) 8
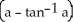
D) 4
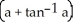
E) 8
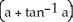

Unlock Deck
Unlock for access to all 105 flashcards in this deck.
Unlock Deck
k this deck


