Deck 6: Regression Analysis

Question 1

This represents which relationship?

A) Positive linear
B) Negative linear
C) No linear
D) Multiple linear

Answer 1

Positive linear

Question 2

The Department of Natural Resources conducted a study examining the condition of fish in the Wolfe River (Wisconsin). In total 110 fish were captured. The variables that were measured are: mile marker of location in river, species (rainbow trout, northern pike, musky, walleye, and panfish ), length, and weight. Which item is not quantitative?

A) amount of fish captured
B) length
C) species
D) mile marker

Answer 2

species

Question 3

In a simple linear regression based on 20 observations, it is found b₁ = 3.20 and se(b₁) = 1.15. Consider the hypothesis : H₀ : $\beta$ ₁ = 0 and H_A : $\beta$ ₁ $\neq$ 0 . Calculate the value of the test statistic.

A) 2.78
B) 2.410
C) 0.415
D) 0.359

Answer 3

2.78

Question 4

In a simple linear regression based on 20 observations, it is found b₁ = 3.25 and se(b₁) = 1.35. Consider the hypothesis: H₀ : $\beta$ ₁ $\neq$ 0 and H_A : $\beta$ ₁ $\neq$ 0 . Calculate the value of the test statistic.

A) 2.41
B) 0.415
C) 1.42
D) 0.121

Question 5

In the following equation $\hat{y}$ = 40,000 + 2x with given sales (y in $500) and marketing (x in dollars), what does the equation imply?

A) An increase of $2 in marketing is associated with an increase of $41,000 in sales.
B) An increase of $1 in marketing is associated with an increase of $1,000 in sales.
C) An increase of $2 in marketing is associated with an increase of $1,000 in sales.
D) An increase of $1 in marketing is associated with an increase of $41,000 in sales.

Question 6

In the following equation $\hat{y}$ = 30,000 + 4x with given sales (y in $500) and marketing (x in dollars), what does the equation imply?

A) An increase of $1 in marketing is associated with an increase of $32,000 in sales.
B) An increase of $1 in marketing is associated with an increase of $2,000 in sales.
C) An increase of $4 in marketing is associated with an increase of $2,000 in sales.
D) An increase of $4 in marketing is associated with an increase of $32,000 in sales.

Question 7

Which of the following is not another name for a predictor variable?

A) control variable
B) independent variable
C) regressors
D) sample variable

Question 8

If R² = 0.42, then how much of the sample variation is y?

A) 3.5%
B) 48.0%
C) 62%
D) 42%

Question 9

If R² = 0.62, then how much of the sample variation is y?

A) 31%
B) 7.8%
C) 38%
D) 62%

Question 10

If SST = 6,000 and SSE = 600, then the coefficient of determination is

A) 0.77
B) 0.43
C) 0.90
D) 0.57

Question 11

If SST = 2,500 and SSE = 575, then the coefficient of determination is

A) 0.43
B) 0.23
C) 0.77
D) 0.57

Question 12

If the coefficient of the determination is 0.61, what is the percent of the R²?

A) 61%
B) 39%
C) -0.61
D) -0.39

Question 13

If the coefficient of the determination is 0.60, what is the percent of the R²?

A) 60%
B) 40%
C) -0.60
D) -0.40

Question 14

In a linear regression, $\varepsilon$ , read as epsilon, is

A) a dummy variable.
B) the unrounded number.
C) the random error.
D) is the relationship between variables.

Question 15

In a linear regression model, the competing hypotheses take all but which form?

A) H₀: $\beta$ _j = $\beta$ _{j0 and} H_A: $\beta$ _j $\neq$ $\beta$ _j0
B) H₀: $\beta$ _j $\le$ $\beta$ _{j0 and} H_A: $\beta$ _j > $\beta$ _j0
C) H₀: $\beta$ _{j $\ge$} $\beta$ _{j0 and} H_A: $\beta$ _j < $\beta$ _j0
D) H₀: $\beta$ _{j >} $\beta$ _{j0 and} H_A: $\beta$ _j $\neq$ $\beta$ _j0

Question 16

The slope coefficient $\beta$ , is called

A) regression.
B) beta.
C) alpha.
D) intercept.

Question 17

Which of the following is not a goodness-of-fit measure?

A) adjusted coefficient of determination
B) coefficient of determination
C) standard error of the estimate
D) simple regression model

Question 18

When determining if there is evidence of a linear relationship between variables, OLS estimators must be __________ for the test to be valid.

A) normally distributed
B) scattered
C) a single variable
D) predicted

Question 19

Based on the following table, what is the sample regression equation?

A) Earnings = 10,625.6413 + 0.3731Cost + 174.0756Grad + 127.3845Debt
B) Earnings = 10,625.6413 + 0.373Cost + 174.0756Grad ? 127.385Debt
C) Earnings = 10,625.6413 ? 0.373Cost + 174.0756Grad ? 127.385Debt
D) Earnings = 10,625.6413 ? 0.373Cost + 174.0756Grad + 127.385 Debt

Question 20

Based on the following table, what is the sample regression equation?

A) Earnings = 10,004.9665 + 0.4349Cost + 178.0989Grad + 141.4783Debt
B) Earnings = 10,004.9665 ? 0.4349Cost + 178.0989Grad + 141.4783Debt
C) Earnings = 10,004.9665 + 0.4349Cost + 178.0989Grad ? 141.4783Debt
D) Earnings = 10,004.9665 ? 0.4349Cost + 178.0989Grad ? 141.4783 Debt

Question 21

If there is a 30,000 average Service Cost in marketing services, with a 70% Cost Increase and 60% of client Payment for services upfront in addition to advantages of City, the predicted annual earnings for the firm are: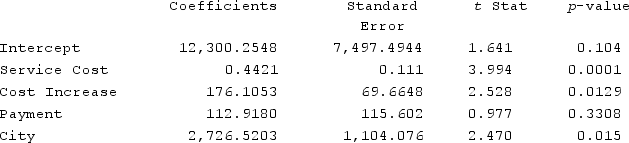

A) $44,665.71
B) $37,890.63
C) $36,722.90
D) $47,392.23

Question 22

If there is a 30,000 average Service Cost in marketing services, with a 70% Cost Increase and 60% of client Payment for services upfront in addition to advantages of City, the predicted annual earnings for the firm are: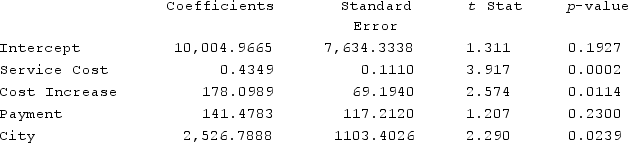

A) $44,007.59
B) $35,518.89
C) $34,351.16
D) $46,534.38

Question 23

If SSE = 180 and SSR = 320, then the coefficient of determination is

A) 0.20
B) 0.64
C) 0.60
D) 0.67

Question 24

If $\hat{y}$ = 120 - 3x with y = product and x = price of product, what happens to the demand if the price is increased by 2 units?

A) increases by 6 units
B) increases by 9 units
C) decreases by 6 units
D) decreases by 9 units

Question 25

If $\hat{y}$ = 110 - 5x with y = product and x = price of product, what happens to the demand if the price is increased by 3 units?

A) increases by 15 units
B) increases by 125 units
C) decreases by 15 units
D) decreases by 95 units

Question 26

The standard error of the estimate is S_e = . What result best fits the sample data?< / p>

A) when S_e = 1.526
B) when S_e = 2.001
C) when S_e = 0.543
D) when S_e = 0.005

Question 27

Based on goodness-of-fit measures, which is the preferred model based on the results below:

A) model 1
B) model 2
C) model 3
D) Both model 1 & model 2

Question 28

In the goodness-of-fit measures, interpret the coefficient of determination for Earnings with Model 3 and what the sample variation of earnings explains.

A) 93.3700% of the sample variation in Earnings is explained by the regression model.
B) 0.8475 of the sample variation in Earnings determines the model selection.
C) 0.01 of the sample variation in Earnings determines the model selection.
D) 71.77% of the sample variation in Earnings is explained by the regression model.

Question 29

In the goodness-of-fit measures, interpret the coefficient of determination for Earnings with Model 3 and what the sample variation of earnings explains.

A) 41.87% of the sample variation in Earnings is explained by the regression model.
B) 0.8475 of the sample variation in Earnings determines the model selection.
C) 0.010 of the sample variation in Earnings determines the model selection.
D) 42.88% of the sample variation in Earnings is explained by the regression model.

Question 30

Based on goodness-of-fit measures, what is the percentage of the sample variation unexplained by Model 2?

A) 81.74%
B) 2.56%
C) 83.61%
D) 18.26%

Question 31

Based on goodness-of-fit measures, what is the percentage of the sample variation unexplained by Model 2?

A) 38.90%
B) 40.23%
C) 41.87%
D) 59.77%

Question 32

Conduct a test to determine if the predictor variables are jointly significant in explaining Earnings at $\alpha$ = 0.05.

A) P(F1,18) $\ge$ 74.608, p-value is less than $\alpha$ = 0.05, we reject H0, but jointly significant in explaining earnings.
B) P(F1,19) $\ge$ 82.818, p-value is less than $\alpha$ = 0.05, we accept H0, jointly do not explain earnings.
C) P(F1,18) $\ge$ 74.608, p-value is less than $\alpha$ = 0.05, we accept H0, but jointly significant in explaining earnings.
D) P(F1,19) $\ge$ 82.818, p-value is less than $\alpha$ = 0.05, we reject H0, jointly do not explain earnings.

Question 33

Conduct a test to determine if the predictor variables are jointly significant in explaining Earnings at $\alpha$ = 0.05.

A) P(F_1,18) $\ge$ 57.737, p-value is less than $\alpha$ = 0.05, we reject H₀, but jointly significant in explaining earnings.
B) P(F_1,19) $\ge$ 60.945, p-value is less than $\alpha$ = 0.05, we accept H₀, but jointly significant in explain earnings.
C) P(F_1,18) $\ge$ 57.737, p-value is less than $\alpha$ = 0.05, we accept H₀, but jointly significant in explaining earnings.
D) P(F_1,19) $\ge$ 60.945, p-value is less than $\alpha$ = 0.05, we reject H₀, jointly do not explain earnings.

Question 34

Camber Seal is a financial planner hired to review KMB stock. She is considering the CAPM where the KMB risk-adjusted stock return R - R_f is used as the response variable and the risk-adjusted market return R_m - R f is used as the predictor variable. KMB stock is considered staple products, whether the economy is good or bad. Given estimates for the beta coefficient is 0.7528, standard error of 0.1600, and a p-value of 0.028 with a formulated hypothesis of H ₀ : $\beta$ $\ge$ 1 H A : $\beta$ < 1. At a 5% significance level, what is the risk determination of the stock against the market?

A) $\beta$ is significantly less than one, thus, H0 : is rejected and less risky than the market.
B) $\beta$ is significantly higher than one, thus, H0 : is accepted and less risky than the market.
C) $\beta$ is significantly less than one, thus, H0 : is accepted and riskier than the market.
D) $\beta$ is significantly higher than one, thus, H0 : is rejected and riskier than the market.

Question 35

Camber Seal is a financial planner hired to review KMB stock. She is considering the CAPM where the KMB risk-adjusted stock return R - R_f is used as the response variable and the risk-adjusted market return R_m - R f is used as the predictor variable. KMB stock is considered staple products, whether the economy is good or bad. Given estimates for the beta coefficient is 0.7503, standard error of 0.1391, and a p-value of 0.039 with a formulated hypothesis of H ₀ : $\beta$ $\ge$ 1 H A : $\beta$ < 1. At a 5% significance level, what is the risk determination of the stock against the market?

A) $\beta$ is significantly less than one, thus, H ₀ : is rejected and less risky than the market.
B) $\beta$ is significantly higher than one, thus, H ₀ : is accepted and less risky than the market.
C) $\beta$ is significantly less than one, thus, H₀ : is accepted and riskier than the market.
D) $\beta$ is significantly higher than one, thus, H₀ : is rejected and riskier than the market.

Question 36

To conduct a test of joint significance, you want to employ which test?

A) regressed mean F test
B) left-tailed F test
C) double-tailed F test
D) right-tailed F test

Question 37

The simple linear regression model y = $\beta$ ₀ + $\beta$ ₁x + $\varepsilon$ implies that if x ________, we expect y to change by $\beta$ ₁, irrespective of the value of x.

A) is a straight line
B) goes down by one unit
C) goes up by one unit
D) curves by one unit

Question 38

Abe is calculating a stock investment risk. If the hypothesis is H₀ : $\beta$ $\ge$ 1 H_A : $\beta$ < 1, and the p-value 0.027, and $\alpha$ = 0.05 is the investment riskier than the market?

A) $\beta$ is equal to one, so the investment is less risky than the market.
B) $\beta$ is more than one, so the investment is riskier than the market.
C) $\beta$ is less than one, so the investment is less risky than the market.
D) $\beta$ is less than one, so the investment is riskier than the market.

Question 39

Which one of the following is not a common violation in the test of validity?

A) estimation
B) multicollinearity
C) changing variability
D) nonlinear patterns

Question 40

In a study where the least squares estimates were based on 34 sets of sample observations, the total sum of squares and regression sum of squares were found to be: SST = 4.32 and SSR = 4.00. What is the error sum of squares?

A) 1.07
B) 0.32
C) 0.929
D) 8.74

Question 41

In a study where the least squares estimates were based on 34 sets of sample observations, the total sum of squares and regression sum of squares were found to be: SST = 4.53 and SSR = 4.21. What is the error sum of squares?

A) 1.07
B) 0.32
C) 0.929
D) 8.74

Question 42

It is important to review residual plots to identify any signs of _____ and correlated observations in cross-sectional and time-series studies.

A) variable studies
B) residual plot crosses
C) changing variability
D) standard error

Question 43

In Excel, to construct a residual plot, input of a y range and an x range is needed. Aimee is examining the relationship between age and square foot range (sqft) of living space. In the scenario provided, what would be the y and what would be the x range data?

A) In selecting a regression, residual plot is the first selection before range input.
B) Input y range would be age and Input x range would be sqft.
C) Input y range would be blank to produce a concise x range.
D) Input y range would be sqft and Input x range would be age.

Question 44

Regression analysis captures the relationship between only two distinct variables.

Question 45

The response variable is the outcome of a variable, whereas the predictor is the input variable(s).

Question 46

Quantitative variables are numeric, whereas qualitative variables are descriptors reflecting categories.

Question 47

R² in linear regression is the correlation coefficient.

Question 48

Analysis of covariance (ANCOVA) is used in the context of linear regression to derive R².

Question 49

The total sum of squares (SST) can be broken into two: explained variation and unexplained variation.

Question 50

When using Excel for a one-tailed test, the returned p-value will need to be divided in half.

Question 51

When working with big data, a sample size is significantly large if the variability virtually disappears.

Question 52

If the Ordinary Lease Squares (OLS) required assumptions of linear regression are met, OLS estimators of the regression coefficients $\beta$ _j are unbiased.

Question 53

If residual plots exhibit strong nonlinear patterns, the inferences made by a linear regression model can be quite accurate.