Deck 5: Production Theory and Estimation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/42
Play
Full screen (f)
Deck 5: Production Theory and Estimation
1
Suppose that three isoquants that represent 10, 20, and 30 units of output are plotted on a graph and a straight line is drawn from the origin through the isoquants. If the portion of the line between the isoquants that represent 10 and 20 units of output is longer than the portion of the line between the isoquants that represent 20 and 30 units of output, then the firm represented by these isoquants
A) has engaged in product innovation.
B) is experiencing increasing returns to scale.
C) is experiencing decreasing returns to scale.
D) will maximize profits by producing 10 units of output.
A) has engaged in product innovation.
B) is experiencing increasing returns to scale.
C) is experiencing decreasing returns to scale.
D) will maximize profits by producing 10 units of output.
is experiencing increasing returns to scale.
2
Production refers to all activities involved in the production of goods and services.
True
3
Scale is a short-run concept.
False
4
The firm plans in the short run and operates in the long run.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
5
The slope of the short-run production function is equal to the average product of the variable input.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
6
The marginal resource cost of an input is equal to the change in total cost that results from hiring an additional unit of a variable input.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
7
Ridge lines drawn on an isoquant map separate Stage II from Stages I and III of production.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
8
Firms will only operate at points on an isoquant map that are between the ridge lines.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
9
The absolute value of the slope of an isoquant is equal to the ratio of the marginal products of the inputs.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
10
The closer an isoquant is to a straight line, the closer the inputs are to being perfect complements.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
11
If the marginal rate of technical substitution is the same at all points on an isoquant, then the two inputs are perfect substitutes.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
12
The absolute value of the slope of the isocost line is equal to the ratio of input prices.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
13
If two isocost lines are parallel, then both have the same input price ratio but the one further from the origin represents a higher level of total cost.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
14
The point of tangency between a convex isoquant and an isocost line represents an optimal combination of inputs.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
15
Every point on an expansion path represents a combination of inputs that minimizes the cost of producing a given level of output.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
16
All expansion paths are straight lines through the origin.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
17
If a firm is maximizing profit, then it must be employing a combination of inputs that is on its expansion path.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
18
If a firm is employing a combination of inputs that is on its expansion path, then it must be maximizing profits.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
19
If the price of an input increases, then the firm will use more of it.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
20
If a firm is experiencing increasing returns to scale, then a doubling of output will require more than a doubling of all inputs.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
21
Decreasing returns to scale arise because of increased specialization and division of labor at higher levels of output.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
22
Most firms operate at a level of output that results in nearly constant returns to scale.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
23
A country will import goods in which it has a comparative advantage and export goods in which it has a comparative disadvantage.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
24
A country that has a relative abundance of cheap labor will tend to have a comparative advantage in the production of goods that are produced using a lot of labor.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
25
Most innovations involve revolutionary departures from previous practices and products.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
26
The product cycle model asserts that innovating firms tend to achieve long-term domination of markets.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
27
Innovation tends to be stimulated by an environment where firms are protected from competitive forces.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
28
American firms generally stress product innovation while Japanese firms stress process innovation.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
29
One disadvantage of modern computerized production methods is that they tend to reduce the optimal lot size, thus reducing total profits.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
30
Most innovations are based on new technologies and ideas.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
31
The use of robots on automobile assembly lines is an example of product innovation.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
32
CAD is an acronym that stands for capital-assisted development.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
33
CAM is an acronym that stands for computer-aided manufacturing.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
34
CAD-CAM allows firms to develop products more rapidly and at a lower cost.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
35
The table below presents estimates of the maximum levels of output possible with various combinations of two inputs.
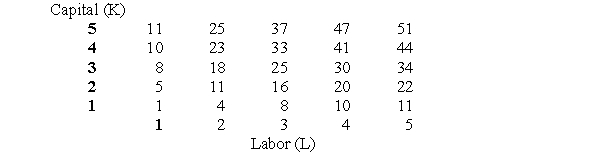 Assume that a unit of output sells for $2 and that the firm currently employs two units of capital (K = 2).
Assume that a unit of output sells for $2 and that the firm currently employs two units of capital (K = 2).
(i) What is the marginal product of labor when L = 4?
(ii) What is the average product of labor when L = 4?
(iii) What is the marginal revenue product of labor when L = 4? What is the output elasticity of labor when L = 4?
(iv) If the wage rate of labor is $10, how many units of labor should the firm hire and how many units of output should it produce?
 Assume that a unit of output sells for $2 and that the firm currently employs two units of capital (K = 2).
Assume that a unit of output sells for $2 and that the firm currently employs two units of capital (K = 2).(i) What is the marginal product of labor when L = 4?
(ii) What is the average product of labor when L = 4?
(iii) What is the marginal revenue product of labor when L = 4? What is the output elasticity of labor when L = 4?
(iv) If the wage rate of labor is $10, how many units of labor should the firm hire and how many units of output should it produce?

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
36
The table below presents estimates of the maximum levels of output possible with various combinations of two inputs.
 Assume that a unit of output sells for $3 and that the firm currently employs three units of capital (K = 3).
Assume that a unit of output sells for $3 and that the firm currently employs three units of capital (K = 3).
(i) What is the marginal product of labor when L = 4?
(ii) What is the average product of labor when L = 4?
(iii) What is the marginal revenue product of labor when L = 4? What is the output elasticity of labor when L = 4?
(iv) If the wage rate of labor is $12, how many units of labor should the firm hire and how many units of output should it produce?
 Assume that a unit of output sells for $3 and that the firm currently employs three units of capital (K = 3).
Assume that a unit of output sells for $3 and that the firm currently employs three units of capital (K = 3).(i) What is the marginal product of labor when L = 4?
(ii) What is the average product of labor when L = 4?
(iii) What is the marginal revenue product of labor when L = 4? What is the output elasticity of labor when L = 4?
(iv) If the wage rate of labor is $12, how many units of labor should the firm hire and how many units of output should it produce?

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
37
The table below presents estimates of the maximum levels of output possible with various combinations of two inputs.
 Assume that a unit of output sells for $5 and that the firm currently employs one unit of capital (K = 1).
Assume that a unit of output sells for $5 and that the firm currently employs one unit of capital (K = 1).
(i) What is the marginal product of labor when L = 2?
(ii) What is the average product of labor when L = 2?
(iii) What is the marginal revenue product of labor when L = 2? What is the output elasticity of labor when L = 2?
(iv) If the wage rate of labor is $10, how many units of labor should the firm hire and how many units of output should it produce?
 Assume that a unit of output sells for $5 and that the firm currently employs one unit of capital (K = 1).
Assume that a unit of output sells for $5 and that the firm currently employs one unit of capital (K = 1).(i) What is the marginal product of labor when L = 2?
(ii) What is the average product of labor when L = 2?
(iii) What is the marginal revenue product of labor when L = 2? What is the output elasticity of labor when L = 2?
(iv) If the wage rate of labor is $10, how many units of labor should the firm hire and how many units of output should it produce?

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
38
The table below presents estimates of the maximum levels of output possible with various combinations of two inputs.
 Assume that a unit of output sells for $10 and that the firm currently employs four units of capital (K = 4).
Assume that a unit of output sells for $10 and that the firm currently employs four units of capital (K = 4).
(i) What is the marginal product of labor when L = 5?
(ii) What is the average product of labor when L = 5?
(iii) What is the marginal revenue product of labor when L = 5? What is the output elasticity of labor when L = 5?
(iv) If the wage rate of labor is $80, how many units of labor should the firm hire and how many units of output should it produce?
 Assume that a unit of output sells for $10 and that the firm currently employs four units of capital (K = 4).
Assume that a unit of output sells for $10 and that the firm currently employs four units of capital (K = 4).(i) What is the marginal product of labor when L = 5?
(ii) What is the average product of labor when L = 5?
(iii) What is the marginal revenue product of labor when L = 5? What is the output elasticity of labor when L = 5?
(iv) If the wage rate of labor is $80, how many units of labor should the firm hire and how many units of output should it produce?

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
39
A firm currently employs 40 production workers and 5 supervisors. The marginal product of the last production worker employed is 36 units of output per hour and production workers are paid $8 per hour. The marginal product of the last supervisor employed is 120 units of output per hour and supervisors are paid $20 per hour. Every employee works 40 hours per week.
(i) What is the firm's total labor cost per week?
(ii) Assume that hours of labor by supervisors (Ls) is plotted on the vertical axis and hours of labor by production workers (Lp) is plotted on the horizontal axis. What is the equation for the firm's isocost line? What are the two intercepts of the isocost line?
(iii) Assume that the firm's isoquants are smooth curves and that labor hours can be varied continuously. Is the firm producing the maximum level of output given its current level of cost? If it is, explain how you can tell. If it isn't, explain what it should do to increase output.
(i) What is the firm's total labor cost per week?
(ii) Assume that hours of labor by supervisors (Ls) is plotted on the vertical axis and hours of labor by production workers (Lp) is plotted on the horizontal axis. What is the equation for the firm's isocost line? What are the two intercepts of the isocost line?
(iii) Assume that the firm's isoquants are smooth curves and that labor hours can be varied continuously. Is the firm producing the maximum level of output given its current level of cost? If it is, explain how you can tell. If it isn't, explain what it should do to increase output.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
40
A firm currently employs 25 production workers and 4 supervisors. The marginal product of the last production worker employed is 50 units of output per hour and production workers are paid $10 per hour. The marginal product of the last supervisor employed is 160 units of output per hour and supervisors are paid $40 per hour. Every employee works 40 hours per week.
(i) What is the firm's total labor cost per week?
(ii) Assume that hours of labor by supervisors (Ls) is plotted on the vertical axis and hours of labor by production workers (Lp) is plotted on the horizontal axis. What is the equation for the firm's isocost line? What are the two intercepts of the isocost line?
(iii) Assume that the firm's isoquants are smooth curves and that labor hours can be varied continuously. Is the firm producing the maximum level of output given its current level of cost? If it is, explain how you can tell. If it isn't, explain what it should do to increase output.
(i) What is the firm's total labor cost per week?
(ii) Assume that hours of labor by supervisors (Ls) is plotted on the vertical axis and hours of labor by production workers (Lp) is plotted on the horizontal axis. What is the equation for the firm's isocost line? What are the two intercepts of the isocost line?
(iii) Assume that the firm's isoquants are smooth curves and that labor hours can be varied continuously. Is the firm producing the maximum level of output given its current level of cost? If it is, explain how you can tell. If it isn't, explain what it should do to increase output.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
41
A firm currently employs 45 production workers and 6 supervisors. The marginal product of the last production worker employed is 50 units of output per hour and production workers are paid $10 per hour. The marginal product of the last supervisor employed is 150 units of output per hour and supervisors are paid $30 per hour. Every employee works 40 hours per week.
(i) What is the firm's total labor cost per week?
(ii) Assume that hours of labor by supervisors (Ls) is plotted on the vertical axis and hours of labor by production workers (Lp) is plotted on the horizontal axis. What is the equation for the firm's isocost line? What are the two intercepts of the isocost line?
(iii) Assume that the firm's isoquants are smooth curves and that labor hours can be varied continuously. Is the firm producing the maximum level of output given its current level of cost? If it is, explain how you can tell. If it isn't, explain what it should do to increase output.
(i) What is the firm's total labor cost per week?
(ii) Assume that hours of labor by supervisors (Ls) is plotted on the vertical axis and hours of labor by production workers (Lp) is plotted on the horizontal axis. What is the equation for the firm's isocost line? What are the two intercepts of the isocost line?
(iii) Assume that the firm's isoquants are smooth curves and that labor hours can be varied continuously. Is the firm producing the maximum level of output given its current level of cost? If it is, explain how you can tell. If it isn't, explain what it should do to increase output.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
42
A firm wants to minimize the cost of producing 2,800 units of output per week. It has hired a production engineer to identify alternative production technologies that will accomplish this goal. The production technologies use the different combinations of capital (K) and labor (L) that are listed below.
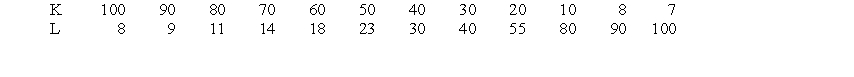 Assume that the rental price of capital is $5 and the wage rate of labor is $4. Determine the minimum cost of producing 2,800 units of output and then show how the combination of inputs that yield the minimum cost can be determined using the marginal approach.
Assume that the rental price of capital is $5 and the wage rate of labor is $4. Determine the minimum cost of producing 2,800 units of output and then show how the combination of inputs that yield the minimum cost can be determined using the marginal approach.
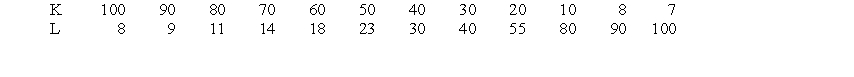 Assume that the rental price of capital is $5 and the wage rate of labor is $4. Determine the minimum cost of producing 2,800 units of output and then show how the combination of inputs that yield the minimum cost can be determined using the marginal approach.
Assume that the rental price of capital is $5 and the wage rate of labor is $4. Determine the minimum cost of producing 2,800 units of output and then show how the combination of inputs that yield the minimum cost can be determined using the marginal approach.
Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck


