Deck 19: Magnetic Forces and Fields
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/33
Play
Full screen (f)
Deck 19: Magnetic Forces and Fields
1
A proton is moving at in a magnetic field of . What is the magnitude of the magnetic force on the proton?
A) 0.0
B)
C)
D)
E) More information is needed.
A) 0.0
B)
C)
D)
E) More information is needed.
More information is needed.
2
A proton is moving perpendicular to a magnetic field at and experiences a magnetic force of magnitude . What is the magnitude of the magnetic field?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
An electron is moving at perpendicular to a uniform magnetic field. What is the radius of its path?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
An electron is moving at perpendicular to a uniform magnetic field. If the radius of the motion is , what is the magnitude of the magnetic field?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
5
A proton cyclotron has a magnetic field of between its poles and a radius of . What is the maximum energy for the protons from this machine?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
6
What is the speed of a proton in a cyclotron having a magnetic field when the proton is at a distance of from the center?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
7
A proton is moving at and experiences a magnetic force of magnitude . If the magnetic field makes an angle of with respect to the velocity of the proton, what is the field's magnitude?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
8
Find the force (magnitude and direction) exerted on an electron moving vertically upward at a speed of by a horizontal magnetic field of directed north.
A) west
B) east
C) east
D) west
A) west
B) east
C) east
D) west

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
9
An electron is moving at at an angle of to a magnetic field. What is the magnitude of the force on the electron?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
10
An electron is moving at at an angle of to a magnetic field. What is the magnitude of the acceleration of the electron?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
11
The magnetic field in a cyclotron is . Find the magnitude of the magnetic force on a proton with velocity of in a plane perpendicular to the field.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
12
The magnetic field in a cyclotron is . What is the radius of the vacuum chamber for a maximum proton velocity of ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
13
An electric field perpendicular to a magnetic field is used as a velocity selector for ions, selecting the velocity . Next, ions are sent through the same velocity selector, selecting velocity . If neither the electric nor magnetic fields have changed between the two processes, how do and compare?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
14
In a velocity selector for ions, when the velocity of the ions is double the value for which the selector is set, how do the magnetic force and the electric force compare?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
15
A flat conductor of thickness is placed in a magnetic field of perpendicular to the flat surface. If there are charge carriers (i.e., electrons) per , what is the Hall voltage generated when 3.40 A flows along the conductor?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
16
A long wire carrying a current of 22 A makes an angle of with the Earth's magnetic field of 0.51 . What is the magnetic force on the wire?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
17
If the magnetic field from a long, straight, current-carrying wire has a magnitude at a distance , what is the magnitude of the field at a distance ?
A) also
B)
C)
D)
E)
A) also
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
18
A power line carries at a height of above the ground. What is the resulting magnetic field at ground level?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
19
Two parallel wires are each carrying and are separated by . If the currents are in opposite directions, what is the magnitude of the magnetic field halfway between them?
A)
B)
C) 0.0
D)
E)
A)
B)
C) 0.0
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
20
If magnetic field inside a solenoid having 100 turns per and a current of is
A) .
B) .
C) .
D) .
E)
A) .
B) .
C) .
D) .
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
21
Two long straight wires each carry a current of . One wire lies on the -axis with its current in the positive -direction. The other wire lies on the -axis with its current in the positive -direction. In the plane, which quadrant (quadrants) has/have points where the magnetic field is zero?
A) I
B) I and III
C) II
D) II and IV
E) none of them
F) all of them
A) I
B) I and III
C) II
D) II and IV
E) none of them
F) all of them

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
22
One wire, lying on the -axis, carries a current of in the positive -direction. Another wire, lying on the -axis, carries a current of in the positive -direction. What is the magnitude of the magnetic field at ( , y) ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
23
A solenoid of radius , carrying a current of , produces a magnetic field at its center of . How many turns per unit length does the solenoid have?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
24
Find the circulation for the path shown.
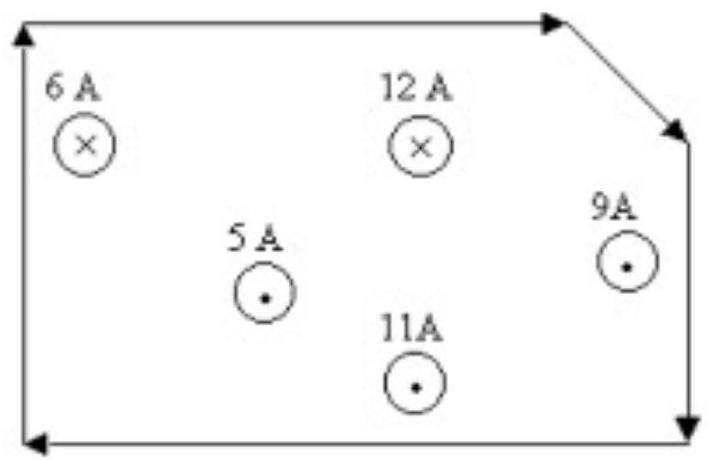
A) A
B) A)
C)
D)
E)

A) A
B) A)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
25
Find the circulation for the path shown.
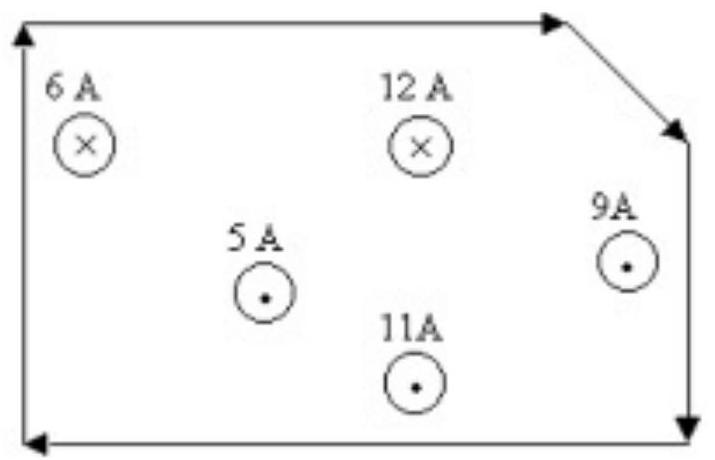
A) A)
B)
C)
D)
E)

A) A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
26
A proton and electron, each travelling with the same velocity, enter a region of uniform magnetic field. They experience
A) forces in the same direction and having ratio .
B) the same force.
C) forces equal in magnitude, but opposite in direction.
D) forces opposite in direction and having ratio .
A) forces in the same direction and having ratio .
B) the same force.
C) forces equal in magnitude, but opposite in direction.
D) forces opposite in direction and having ratio .

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
27
A proton and electron, travelling with the same velocity in the direction, enter separate regions, each with a uniform magnetic field in the direction (magnitude for the proton, for the electron). They each experience the same acceleration. What can we conclude?
A) The magnetic fields were in the same direction and have ratio .
B) The magnetic fields were in the opposite direction and have ratio .
C) The magnetic fields were identical in magnitude and direction.
D) The magnetic fields were in the opposite direction and have ratio .
E) The magnetic fields were identical in magnitude and opposite in direction.
F) The magnetic fields were in the same direction and have ratio .
A) The magnetic fields were in the same direction and have ratio .
B) The magnetic fields were in the opposite direction and have ratio .
C) The magnetic fields were identical in magnitude and direction.
D) The magnetic fields were in the opposite direction and have ratio .
E) The magnetic fields were identical in magnitude and opposite in direction.
F) The magnetic fields were in the same direction and have ratio .

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
28
A proton and electron, each travelling with the same velocity in the direction, enter a region of uniform magnetic field in the direction. If the acceleration of the electron is in the direction, what is the acceleration of the proton?
A) in the direction
B) in the direction
C) in the direction
D) in the direction
E) in the direction
F) in the direction
A) in the direction
B) in the direction
C) in the direction
D) in the direction
E) in the direction
F) in the direction

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
29
A cyclotron is designed to accelerate protons (mass ) up to a kinetic energy of . If the magnetic field in the cyclotron is , what is the radius of the dipole magnets in the cyclotron?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
30
A cyclotron is designed to accelerate protons (mass ) up to a kinetic energy of . If the radius of the dipole magnets is , what is the magnetic field used in the cyclotron?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
31
A cyclotron is designed to accelerate protons to a maximum kinetic energy K. Assuming one then tried to accelerate alpha particles (about four times the mass and twice the charge), what kinetic energy could be achieved?
A)
B)
C)
D)
E)
F)
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
32
A charged particle of mass enters a region of uniform magnetic field at a speed of , at an angle of 37 degrees relative to the magnetic field direction. If the magnetic field strength is and the charge of the particle is , what will be the radius of the helical path it takes?
A)
B) Insufficient information is given.
C)
D)
A)
B) Insufficient information is given.
C)
D)

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck
33
A charged particle of mass enters a region of uniform magnetic field at a speed of , at an angle of 37 degrees relative to the magnetic field direction. If the magnetic field strength is what will be the radius of the helical path it takes?
A) .
B)
C)
D) Insufficient information given.
A) .
B)
C)
D) Insufficient information given.

Unlock Deck
Unlock for access to all 33 flashcards in this deck.
Unlock Deck
k this deck


