Deck 8: Systems of Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/102
Play
Full screen (f)
Deck 8: Systems of Equations and Inequalities
1
The length of a rectangle is 9 in. more than twice its width. If the perimeter of the rectangle is 54 in., find the width of the rectangle.
A) 5 in.
B) 6 in.
C) 7 in.
D) 8 in.
A) 5 in.
B) 6 in.
C) 7 in.
D) 8 in.
6 in.
2
Solve using any method and identify the system as consistent, inconsistent, or dependent. 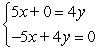
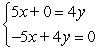
{(x, y) | 5x + 0 = 4y}; consistent/dependent
3
Solve using any method and identify the system as consistent, inconsistent, or dependent. 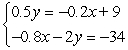
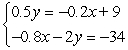
Ø; inconsistent
4
Adult tickets for a play cost $9 and child tickets cost $1. If there were 22 people at a performance and the theatre collected $182 from ticket sales, how many children attended the play?
A) 1 child
B) 2 children
C) 3 children
D) 20 children
A) 1 child
B) 2 children
C) 3 children
D) 20 children

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
5
Substitute the x- and y-values indicated by the ordered pair (-3, -2) to determine if it solves the system. 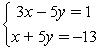
A) Yes
B) No
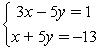
A) Yes
B) No

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
6
Solve using any method and identify the system as consistent, inconsistent, or dependent. 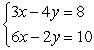
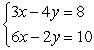

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the system using substitution. Write your answer as an ordered pair. 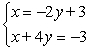
A) (9, -3)
B) (8, -3)
C) (9, -2)
D) (8, -2)
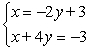
A) (9, -3)
B) (8, -3)
C) (9, -2)
D) (8, -2)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the system by graphing. If the solution does not appear to be a lattice point, estimate the solution to the nearest tenth (indicate that your solution is an estimate) 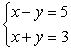
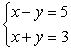

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the system using substitution. Write your answer as an ordered pair. 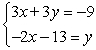

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the system by graphing. If the solution does not appear to be a lattice point, estimate the solution to the nearest tenth (indicate that your solution is an estimate). 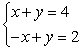

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the system by elimination. 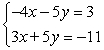
A) (8, -8)
B) (9, -7)
C) (8, -7)
D) (9, -8)
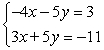
A) (8, -8)
B) (9, -7)
C) (8, -7)
D) (9, -8)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
12
Identify the equation and variable that makes the substitution method easiest to use. Then solve the system. 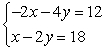
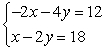

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the system by elimination. The system must first be written in standard form. 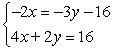
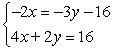

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
14
Solve using any method and identify the system as consistent, inconsistent, or dependent. 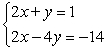
A) (-1, 3); consistent/independent
B) (-1, 3); consistent/dependent
C) {(-1, 3) | 2x + y = 1}; consistent/dependent
D) Ø; inconsistent
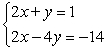
A) (-1, 3); consistent/independent
B) (-1, 3); consistent/dependent
C) {(-1, 3) | 2x + y = 1}; consistent/dependent
D) Ø; inconsistent

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the system by graphing. If the solution does not appear to be a lattice point, estimate the solution to the nearest tenth (indicate that your solution is an estimate). 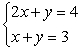

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
16
Whitney invested $8,000, part at 14% and part at 8%. If the total interest at the end of the year is $940, how much did she invest at each rate?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
17
Substitute the x- and y-values indicated by the ordered pair (9, -5) to determine if it solves the system. 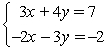
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the system by graphing. If the solution does not appear to be a lattice point, estimate the solution to the nearest tenth (indicate that your solution is an estimate). 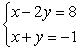

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the system by graphing. If the solution does not appear to be a lattice point, estimate the solution to the nearest tenth (indicate that your solution is an estimate). 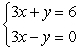

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
20
Find any four ordered triples that satisfy the equation.
x - y + z = -3
x - y + z = -3

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the linear inequality by shading the appropriate half plane.
-3x + y 0
-3x + y 0

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
22
Solve using the elimination method. If the system is inconsistent or dependent, so state. For a system with linear dependence, write the answer in terms of a parameter. For coincident dependence, state the solution in set notation. 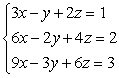
A) (-2, -1, 3)
B) (-z + 1, -z + 2, z)
C)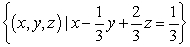
D) no solution, inconsistent
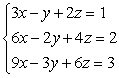
A) (-2, -1, 3)
B) (-z + 1, -z + 2, z)
C)
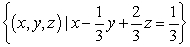
D) no solution, inconsistent

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
23
Determine if the ordered triple (2, -1, 1) is a solution of the system. 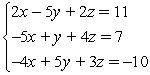
A) Yes
B) No
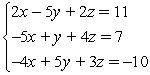
A) Yes
B) No

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
24
A coin jar contains nickels, dimes, and quarters. There are 38 coins in all. There are 2 more nickels than quarters. The value of the dimes is $2.70 less than the value of the quarters. How many coins of each type are in the jar?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the system using the elimination method. If the system is inconsistent or dependent, so state. 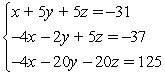
A) (4, -2, -5)
B) (4, -3, -4)
C) dependent
D) no solution, inconsistent
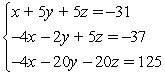
A) (4, -2, -5)
B) (4, -3, -4)
C) dependent
D) no solution, inconsistent

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
26
Determine whether the ordered pair (0, 0) is a solution. 10x - 3y > 5
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the system using elimination and back-substitution. 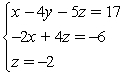

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the linear inequality by shading the appropriate half plane.
x - y 2
x - y 2

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
29
Decompose the rational expression into partial fractions. 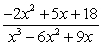

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
30
Solve using the elimination method. If the system is inconsistent or dependent, so state. For a system with linear dependence, write the answer in terms of a parameter. For coincident dependence, state the solution in set notation. 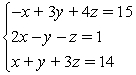
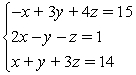

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the system using the elimination method. 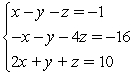
A) (4, 0, 4)
B) (3, 1, 4)
C) (3, 1, 3)
D) (4, 0, 3)
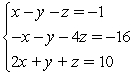
A) (4, 0, 4)
B) (3, 1, 4)
C) (3, 1, 3)
D) (4, 0, 3)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the system using the elimination method. If the system is inconsistent or dependent, so state. For systems with linear dependence, write the answer as an ordered triple in terms of a parameter. 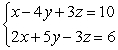

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the system using the elimination method. If the system has coincident dependence, state the solution in set notation. 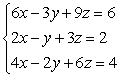

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the linear inequality by shading the appropriate half plane.
2x + 3y > 6
2x + 3y > 6

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
35
Decompose the rational expression into partial fractions. 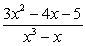
A)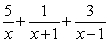
B)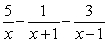
C)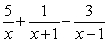
D)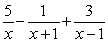
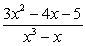
A)
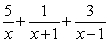
B)
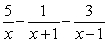
C)
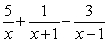
D)
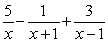

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the linear inequality by shading the appropriate half plane.
3x + y 5
3x + y 5

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
37
Decompose the rational expression into partial fractions. 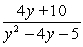
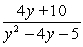

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
38
Determine if the ordered triple (0, -2, 1) is a solution of the system. 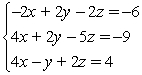
A) Yes
B) No
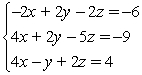
A) Yes
B) No

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the system using elimination. If the system is linearly dependent, state the general solution in terms of a parameter. 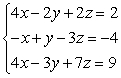
A) (-1, -7, 0)
B) (3, 3, 2)
C) (2z - 3, 5z - 7, z)
D) no solution, inconsistent
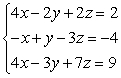
A) (-1, -7, 0)
B) (3, 3, 2)
C) (2z - 3, 5z - 7, z)
D) no solution, inconsistent

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
40
Solve using the elimination method. If the system is inconsistent or dependent, so state. For a system with linear dependence, write the answer in terms of a parameter. For coincident dependence, state the solution in set notation. 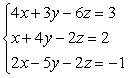
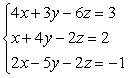

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the system of inequalities by graphing the solution region. 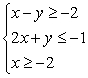
A)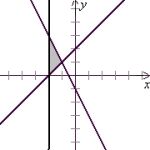
(Tickmarks are spaced one unit apart.)
B)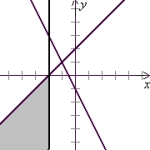
(Tickmarks are spaced one unit apart.)
C)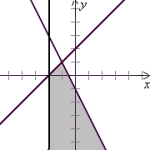
(Tickmarks are spaced one unit apart.)
D)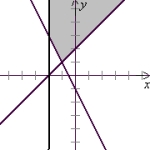
(Tickmarks are spaced one unit apart.)
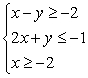
A)

(Tickmarks are spaced one unit apart.)
B)

(Tickmarks are spaced one unit apart.)
C)

(Tickmarks are spaced one unit apart.)
D)

(Tickmarks are spaced one unit apart.)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
42
Determine the size of the matrix and identify the entry located in the second row and first column. 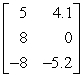
A) 3 * 2; 8
B) 2 * 3; 8
C) 3 * 2; 4.1
D) 2 * 3; 4.1

A) 3 * 2; 8
B) 2 * 3; 8
C) 3 * 2; 4.1
D) 2 * 3; 4.1

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the system of inequalities by graphing the solution region. 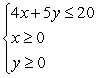
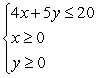

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the system of inequalities by graphing the solution region. 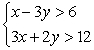
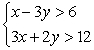

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
45
Write the system of equations for the matrix. Then use back-substitution to find its solution. 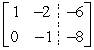
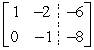

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
46
Determine whether the ordered pairs given are solutions to the system. 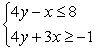 (0, 0), (3, -1), (-3, -3), and (-5, 1)
(0, 0), (3, -1), (-3, -3), and (-5, 1)
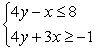 (0, 0), (3, -1), (-3, -3), and (-5, 1)
(0, 0), (3, -1), (-3, -3), and (-5, 1)
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the system of inequalities by graphing the solution region. 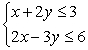
A)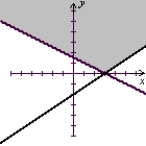
(Tickmarks are spaced one unit apart.)
B)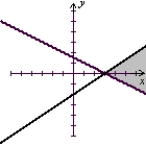
(Tickmarks are spaced one unit apart.)
C)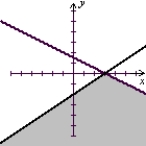
(Tickmarks are spaced one unit apart.)
D)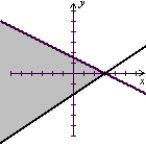
(Tickmarks are spaced one unit apart.)
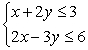
A)

(Tickmarks are spaced one unit apart.)
B)

(Tickmarks are spaced one unit apart.)
C)

(Tickmarks are spaced one unit apart.)
D)

(Tickmarks are spaced one unit apart.)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
48
Determine the size of the matrix and identify the entry located in the second row and first column. 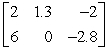
A) 3 * 2; 6
B) 2 * 3; 6
C) 3 * 2; 1.3
D) 2 * 3; 1.3
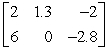
A) 3 * 2; 6
B) 2 * 3; 6
C) 3 * 2; 1.3
D) 2 * 3; 1.3

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the system of inequalities by graphing the solution region. 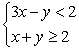
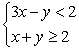

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
50
Perform the indicated row operation, then write the new matrix. 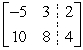 -2R1 + R2 → R2
-2R1 + R2 → R2
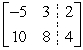 -2R1 + R2 → R2
-2R1 + R2 → R2
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
51
Use the following to answer questions : 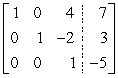
Use back-substitution to find the solution.
A) (27, -7, -5)
B) (-5, -7, 27)
C) (25, -7, -5)
D) (-5, -7, 25)
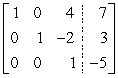
Use back-substitution to find the solution.
A) (27, -7, -5)
B) (-5, -7, 27)
C) (25, -7, -5)
D) (-5, -7, 25)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
52
Form the augmented matrix, then name the diagonal entries of the coefficient matrix. 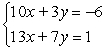
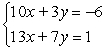

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the system of inequalities by graphing the solution region. 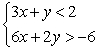
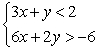

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the system of inequalities by graphing the solution region. 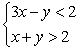

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
55
A stationary store sells rolls of standard gift wrap and deluxe gift wrap. They can stock a total of 110 rolls of gift wrap, of which at least 40 must be standard wrap and at least 20 must be deluxe wrap. The profit on a roll of standard wrap is $4 and the profit on a roll of deluxe wrap is $5. How many rolls of each type of gift wrap should the store stock to maximize their profit?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
56
Use the following to answer questions :
Esther wants to spend no more than $60 buying gifts for her friends Barb and Wanda. She wants to spend at least $20 on Wanda's gift.
Solve the system of linear inequalities.
A)
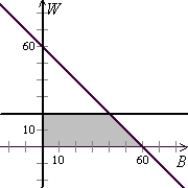
B)
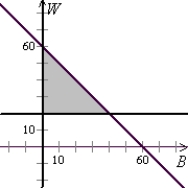
C)
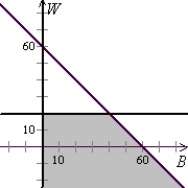
D)
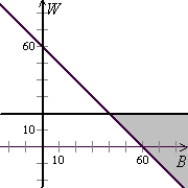
Esther wants to spend no more than $60 buying gifts for her friends Barb and Wanda. She wants to spend at least $20 on Wanda's gift.
Solve the system of linear inequalities.
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
57
Use the following to answer questions : 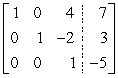
Write the system of equations corresponding to the matrix.
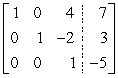
Write the system of equations corresponding to the matrix.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
58
Use the following to answer questions :
Esther wants to spend no more than $60 buying gifts for her friends Barb and Wanda. She wants to spend at least $20 on Wanda's gift.
Let B represent the amount Esther spends on Barb's gift and W represent the amount she spends on Wanda's gift. Write a system of linear inequalities that models the information.
A)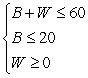
B)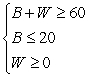
C)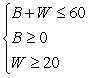
D)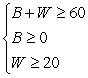
Esther wants to spend no more than $60 buying gifts for her friends Barb and Wanda. She wants to spend at least $20 on Wanda's gift.
Let B represent the amount Esther spends on Barb's gift and W represent the amount she spends on Wanda's gift. Write a system of linear inequalities that models the information.
A)
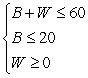
B)
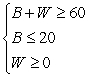
C)
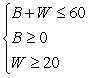
D)
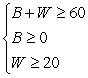

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
59
Determine which of the ordered pairs given produces the maximum value of P(x, y). P(x, y) = 20x + 50y; (0, 0), (5, 2), (4, 0), (0, 6)
A) (0, 0)
B) (5, 2)
C) (4, 0)
D) (0, 6)
A) (0, 0)
B) (5, 2)
C) (4, 0)
D) (0, 6)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
60
Form the augmented matrix, then name the diagonal entries of the coefficient matrix. 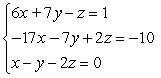
A)
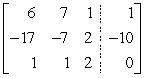
Diagonal entries 6, -7, 2
B)
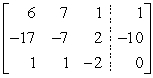
Diagonal entries 6, -7, -2
C)
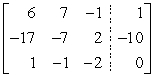
Diagonal entries 6, -7, -2
D)
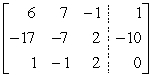
Diagonal entries 6, -7, 2
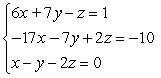
A)
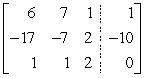
Diagonal entries 6, -7, 2
B)
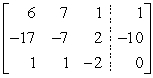
Diagonal entries 6, -7, -2
C)
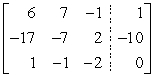
Diagonal entries 6, -7, -2
D)
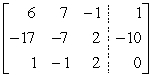
Diagonal entries 6, -7, 2

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
61
Perform the indicated operation, if possible. Do not use a calculator. 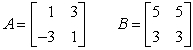 AB
AB
A)
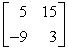
B)
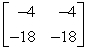
C)
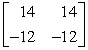
D) matrix multiplication not possible
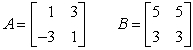 AB
ABA)
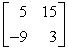
B)
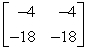
C)
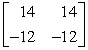
D) matrix multiplication not possible

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
62
Perform the indicated operation, if possible. Do not use a calculator. If the operation cannot be completed, state why. 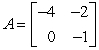 A2
A2
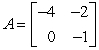 A2
A2
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
63
Perform the indicated operation, if possible. Do not use a calculator. 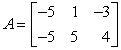 A2
A2
A)
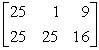
B)

C)
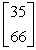
D) matrix multiplication not possible
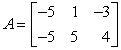 A2
A2A)
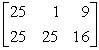
B)

C)

D) matrix multiplication not possible

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
64
Perform the indicated operation, if possible. Do not use a calculator. If the operation cannot be completed, state why. 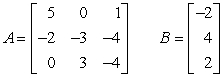 AB
AB
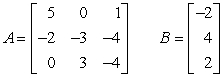 AB
AB
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the system by triangularizing the augmented matrix and using back substitution. If the system is linearly dependent, give the solution in terms of a parameter. 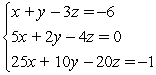
A) (2, 1, 3)
B) (2, 1, 2)
C) coincident dependence; {(x, y, z) | x + y - 3z = -6}
D) no solution, inconsistent
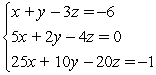
A) (2, 1, 3)
B) (2, 1, 2)
C) coincident dependence; {(x, y, z) | x + y - 3z = -6}
D) no solution, inconsistent

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
66
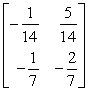
Find the inverse of the 2 * 2 matrix using matrix multiplication, equality of matrices, and a system of equations. 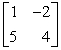
A)
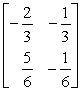
B)
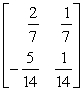
C)
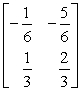
D)
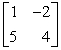
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
67
Model the problem using a system of linear equations. Then solve using the augmented matrix. Suppose $24,000 is invested in three different accounts paying 3%, 4%, and 7%
Annual interest. The interest earned after 1 year is $1270, and the amount
Invested at 7% is equal to the sum of the amounts invested at 3% and 4%.
Find the amount invested at 3%.
A) $5000
B) $6000
C) $7000
D) $8000
Annual interest. The interest earned after 1 year is $1270, and the amount
Invested at 7% is equal to the sum of the amounts invested at 3% and 4%.
Find the amount invested at 3%.
A) $5000
B) $6000
C) $7000
D) $8000

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
68
Perform the indicated operation, if possible. Do not use a calculator. If the operation cannot be completed, state why. 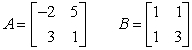 2A - 3B
2A - 3B
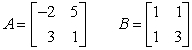 2A - 3B
2A - 3B
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
69
Find the values of a, b, and c that will make the statement true. 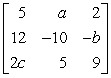 =
= 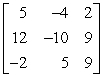
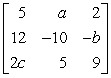 =
= 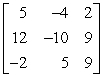

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
70
Perform the indicated operation, if possible. Do not use a calculator. If an operation cannot be completed, state why. 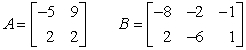 A + B
A + B
A)
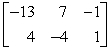
B)
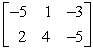
C)
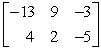
D) different orders, sum not possible
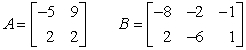 A + B
A + BA)
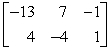
B)
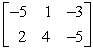
C)
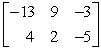
D) different orders, sum not possible

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the system by triangularizing the augmented matrix and using back substitution. If the system is linearly dependent, give the solution in terms of a parameter. 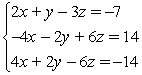
A) (1, -3, 2)
B) (1, -3, 1)
C) coincident dependence; {(x, y, z) | 2x + y - 3z = -7}
D) no solution, inconsistent
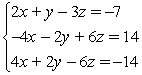
A) (1, -3, 2)
B) (1, -3, 1)
C) coincident dependence; {(x, y, z) | 2x + y - 3z = -7}
D) no solution, inconsistent

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
72
Perform the indicated operation(s), if possible. Do not use a calculator. If the operation cannot be completed, state why. 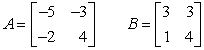 AB and BA
AB and BA
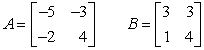 AB and BA
AB and BA
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
73
Perform the indicated operation, if possible. Do not use a calculator. If the operation cannot be completed, state why. 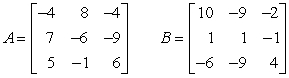 A + B
A + B
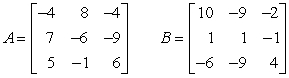 A + B
A + B
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the system by triangularizing the augmented matrix and using back substitution. 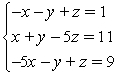
A) (-2, -2, -3)
B) (-2, -2, -2)
C) (-1, -3, -2)
D) (-1, -3, -3)
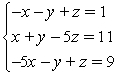
A) (-2, -2, -3)
B) (-2, -2, -2)
C) (-1, -3, -2)
D) (-1, -3, -3)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
75
Perform the indicated row operations, then write the new matrix. 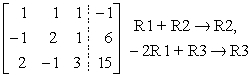
A)
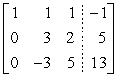
B)
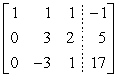
C)
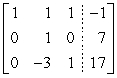
D)
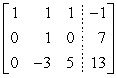
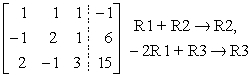
A)
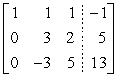
B)
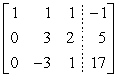
C)
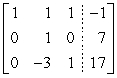
D)
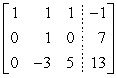

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the system by triangularizing the augmented matrix and using back substitution. If the system is linearly dependent, give the solution in terms of a parameter. 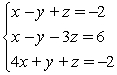
A) (0, 0, -3)
B) (0, 0, -2)
C) coincident dependence; {(x, y, z) | x - y + z = -2}
D) no solution, inconsistent
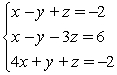
A) (0, 0, -3)
B) (0, 0, -2)
C) coincident dependence; {(x, y, z) | x - y + z = -2}
D) no solution, inconsistent

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
77
What row operation would produce zero beneath the first entry in the diagonal? 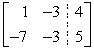
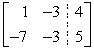

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the system by triangularizing the augmented matrix and using back substitution. 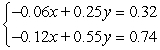
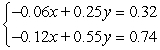

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
79
Perform the indicated operation, if possible. Do not use a calculator. If the operation cannot be completed, state why. 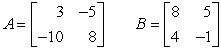 A + B
A + B
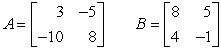 A + B
A + B
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the system by triangularizing the augmented matrix and using back substitution. 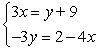
A) (5, 5)
B) (6, 6)
C) (6, 5)
D) (5, 6)
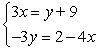
A) (5, 5)
B) (6, 6)
C) (6, 5)
D) (5, 6)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck


