Deck 4: Extension E: Applications of Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/12
Play
Full screen (f)
Deck 4: Extension E: Applications of Differentiation
1
What is the minimum vertical distance between the parabolas 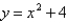 and
and 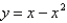 ?
?
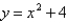 and
and 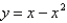 ?
?31/8
2
A steel pipe is being carried down a hallway 14 ft wide.At the end of the hall there is a right-angled turn into a narrower hallway 6 ft wide.What is the length of the longest pipe that can be carried horizontally around the corner? 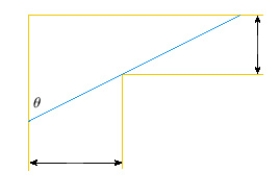

27.50 ft
3
Find the maximum area of a rectangle that can be circumscribed about a given rectangle with length L = 8 and width W = 3. 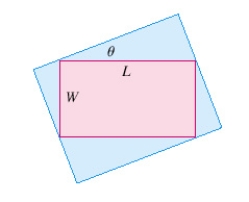

60.5
4
The sum of two positive numbers is 16. What is the smallest possible value of the sum of their squares?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
5
A farmer with 710 ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle.What is the largest possible total area of the four pens?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
6
Find the dimensions of the rectangle of largest area that can be inscribed in an equilateral triangle of side L = 9 cm if one side of the rectangle lies on the base of the triangle. Round your answer to the nearest tenth.
A) 5.5 cm, 4.4 cm
B) 4 cm, 3.91 cm
C) 4.5 cm, 4 cm
D) 4.5 cm, 3.9 cm
E) 7.5 cm, 2.9 cm
F) 9.5 cm, 3.9 cm
A) 5.5 cm, 4.4 cm
B) 4 cm, 3.91 cm
C) 4.5 cm, 4 cm
D) 4.5 cm, 3.9 cm
E) 7.5 cm, 2.9 cm
F) 9.5 cm, 3.9 cm

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
7
A woman at a point A on the shore of a circular lake with radius 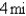 wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time.She can walk at the rate of
wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time.She can walk at the rate of 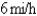 and row a boat at
and row a boat at 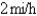 How should she proceed? (Find
How should she proceed? (Find 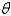 ).Round the result,if necessary,to the nearest hundredth.
).Round the result,if necessary,to the nearest hundredth. 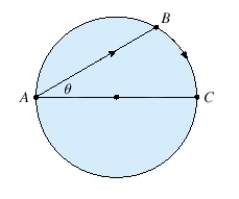
A)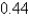 radians
radians
B) She should row from point A to point C radians
C)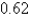 radians
radians
D)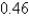 radians
radians
E) She should walk around the lake from point A to point C.
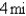 wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time.She can walk at the rate of
wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time.She can walk at the rate of 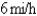 and row a boat at
and row a boat at 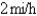 How should she proceed? (Find
How should she proceed? (Find 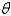 ).Round the result,if necessary,to the nearest hundredth.
).Round the result,if necessary,to the nearest hundredth. 
A)
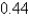 radians
radiansB) She should row from point A to point C radians
C)
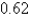 radians
radiansD)
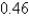 radians
radiansE) She should walk around the lake from point A to point C.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
8
Find two positive numbers whose product is 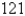 and whose sum is a minimum.
and whose sum is a minimum.
A)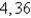
B) 3, 48
C)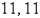
D) 6, 24
E) 2, 72
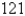 and whose sum is a minimum.
and whose sum is a minimum.A)
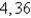
B) 3, 48
C)
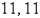
D) 6, 24
E) 2, 72

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
9
Find an equation of the line through the point (8,16) that cuts off the least area from the first quadrant.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
10
A rectangular storage container with an open top is to have a volume of 10 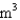 The length of its base is twice the width.Material for the base costs $12 per square meter.Material for the sides costs $5 per square meter.Find the cost of materials for the cheapest such container.
The length of its base is twice the width.Material for the base costs $12 per square meter.Material for the sides costs $5 per square meter.Find the cost of materials for the cheapest such container.
A) $158.1
B) $153.92
C) $152.4
D) $153.9
E) $152.9
F) $151.6
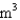 The length of its base is twice the width.Material for the base costs $12 per square meter.Material for the sides costs $5 per square meter.Find the cost of materials for the cheapest such container.
The length of its base is twice the width.Material for the base costs $12 per square meter.Material for the sides costs $5 per square meter.Find the cost of materials for the cheapest such container.A) $158.1
B) $153.92
C) $152.4
D) $153.9
E) $152.9
F) $151.6

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
11
Find the point on the line 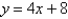 that is closest to the origin.
that is closest to the origin.
A)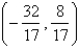
B)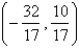
C)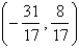
D)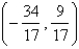
E)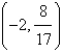
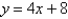 that is closest to the origin.
that is closest to the origin.A)
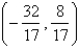
B)
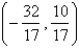
C)
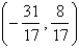
D)
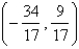
E)
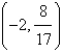

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
12
A piece of wire 10 m long is cut into two pieces.One piece is bent into a square and the other is bent into an equilateral triangle.How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
A) 4.35 m
B) 3.25 m
C) 0 m
D) 5.35 m
E) 4.4 m
A) 4.35 m
B) 3.25 m
C) 0 m
D) 5.35 m
E) 4.4 m

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck


