Deck 14: Section 2: Sequences and Series Available Online at Www.mhhe.com/dugopolski
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/21
Play
Full screen (f)
Deck 14: Section 2: Sequences and Series Available Online at Www.mhhe.com/dugopolski
1
Complete the rewriting of the given series using the new index as indicated. 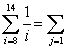
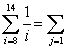
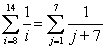
2
Write the given series in summation notation. Use the index i, and let i begin at 1.
ln(6) + ln(7) + ln(8)
ln(6) + ln(7) + ln(8)
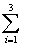
ln(i + 5)
3
Find the sum of the given infinite geometric series. 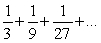
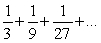
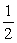
4
Find the sum of the given series. 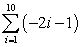
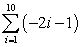

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
5
Find r for the geometric sequence that has a1 = 3 and a4 = 192.

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
6
Write a formula for the general term of the given sequence and match your result to the correct answer below.
-4, -3, -2, -1, 0, ...
-4, -3, -2, -1, 0, ...

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
7
Use the binomial theorem to expand the given binomial.
(b + 2)4
(b + 2)4

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
8
List all terms of the finite sequence an = 3n + 2 for 1 ≤ n ≤ 5.

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
9
List the first four terms of the given sequence and match your result to the correct answer below.
cn = (-1)n(-4n + 3)2
cn = (-1)n(-4n + 3)2

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
10
Find the sum of the given geometric series. 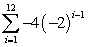
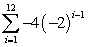

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
11
Find 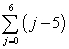 .
.
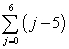 .
.
Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
12
List all terms of the given finite sequence and match your result to the correct answer below.
cn = (-2)n-3 for 3 n 7
cn = (-2)n-3 for 3 n 7

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
13
Write the first five terms of the arithmetic sequence whose nth term is given.
an = -1 + (n + 1)(2)
an = -1 + (n + 1)(2)

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
14
Write a formula for the nth term of the given geometric sequence.
3, -9, 27, ...
3, -9, 27, ...

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
15
Find 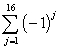 .
.
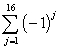 .
.
Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
16
Write the first four terms of the geometric sequence whose nth term is given.
an = (-3)n-1
an = (-3)n-1

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
17
Suppose a deposit of $2000 is made at the beginning of each year for 45 years into an account that pays 11% compounded annually. What is the amount of this annuity at the end of the 45th year?

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate 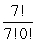 .
.
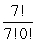 .
.
Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
19
Each time an aluminum beverage can is recycled, some amount of the material is lost due to a variety of reasons. If each recycling step is 80% efficient, what percent of the original material remains if a can is recycled 3 times? Round to the nearest tenth of a percent.

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
20
Write a formula for the nth term of the given arithmetic sequence.
1, 7, 13, 19, 25, . . .
1, 7, 13, 19, 25, . . .

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
21
Use the binomial theorem to write out the first four terms of the given binomial.
(x2 + 1)22
(x2 + 1)22

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck


