Deck 18: Probability Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/30
Play
Full screen (f)
Deck 18: Probability Models
1
A collection of possible outcomes from a random phenomenon is called
A) a standard deviation.
B) a median.
C) an event.
D) an average.
E) a probability.
A) a standard deviation.
B) a median.
C) an event.
D) an average.
E) a probability.
an event.
2
If a coin has 0.6 probability of coming up tails, the probability that it comes up heads is
A) 0.5.
B) -0.2.
C) 0.4.
D) 0.6.
E) 1.0.
A) 0.5.
B) -0.2.
C) 0.4.
D) 0.6.
E) 1.0.
0.4.
3
Here is an assignment of probabilities to the face that comes up when rolling a die once:

Which of the following is true?
A) This isn't a legitimate assignment of probability, because every face of a die must have probability 1/6.
B) This isn't a legitimate assignment of probability, because it gives probability zero to rolling a 3 or a 5.
C) This isn't a legitimate assignment of probability, because the probabilities do not add to exactly 1.
D) This isn't a legitimate assignment of probability, because we must actually roll the die many times to learn the true probabilities.
E) This is a legitimate assignment of probability.

Which of the following is true?
A) This isn't a legitimate assignment of probability, because every face of a die must have probability 1/6.
B) This isn't a legitimate assignment of probability, because it gives probability zero to rolling a 3 or a 5.
C) This isn't a legitimate assignment of probability, because the probabilities do not add to exactly 1.
D) This isn't a legitimate assignment of probability, because we must actually roll the die many times to learn the true probabilities.
E) This is a legitimate assignment of probability.
This is a legitimate assignment of probability.
4
In many popular board games, a player rolls two dice and moves the number of spaces equal to the sum shown on the dice. Here is the assignment of probabilities to the sum of the numbers on the up faces when two fair dice are rolled: 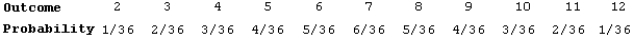 Suppose Scott rolls a sum of 9 on his first roll. What is the probability that Jennifer will have the same sum on her first roll?
Suppose Scott rolls a sum of 9 on his first roll. What is the probability that Jennifer will have the same sum on her first roll?
A) 0
B) 4/6
C) 4/36
D) 9/36
E) 30/36
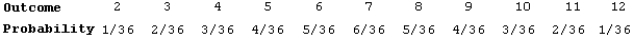 Suppose Scott rolls a sum of 9 on his first roll. What is the probability that Jennifer will have the same sum on her first roll?
Suppose Scott rolls a sum of 9 on his first roll. What is the probability that Jennifer will have the same sum on her first roll?A) 0
B) 4/6
C) 4/36
D) 9/36
E) 30/36

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
5
If an American household were chosen at random and asked how many tablet computers it owned, here are the probabilities as determined by a recent survey:
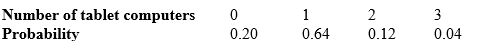
This is a legitimate assignment of probabilities because it satisfies these rules:
A) all the probabilities are between 0 and 1.
B) all the probabilities are between -1 and 1.
C) the sum of all the probabilities is exactly 1.
D) All the probabilities are between 0 and 1, and the sum of all the probabilities is exactly 1.
E) All the probabilities are between -1 and 1, and the sum of all the probabilities is exactly 1..
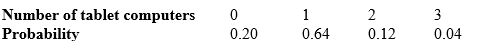
This is a legitimate assignment of probabilities because it satisfies these rules:
A) all the probabilities are between 0 and 1.
B) all the probabilities are between -1 and 1.
C) the sum of all the probabilities is exactly 1.
D) All the probabilities are between 0 and 1, and the sum of all the probabilities is exactly 1.
E) All the probabilities are between -1 and 1, and the sum of all the probabilities is exactly 1..

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
6
If we roll a pair of fair dice and count the number of aces (one dot) showing, the probability model is as follows:

Back in the 17th century, some gamblers thought that the probability of at least one ace (i.e., one or more aces) when rolling two dice was 1/6 + 1/6. Is that true?
A) Yes.
B) No, it's larger than 1/6 + 1/6.
C) No, it's smaller than 1/6 + 1/6.
D) Sometimes it's larger and sometimes it's smaller.
E) Impossible to say.

Back in the 17th century, some gamblers thought that the probability of at least one ace (i.e., one or more aces) when rolling two dice was 1/6 + 1/6. Is that true?
A) Yes.
B) No, it's larger than 1/6 + 1/6.
C) No, it's smaller than 1/6 + 1/6.
D) Sometimes it's larger and sometimes it's smaller.
E) Impossible to say.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
7
If an American household were chosen at random and asked how many tablet computers it owned, here are the probabilities as determined by a recent survey:
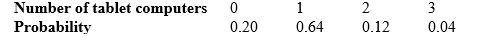
What is the probability that a randomly chosen household owns fewer than two tablet computers?
A) 0.20
B) 0.64
C) 0.84
D) 0.96
E) It is not possible to tell from the given information.
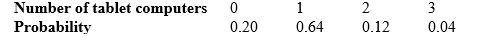
What is the probability that a randomly chosen household owns fewer than two tablet computers?
A) 0.20
B) 0.64
C) 0.84
D) 0.96
E) It is not possible to tell from the given information.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
8
A game involving a pair of dice pays you $4 with probability 16/36, costs you $2 with probability 14/36, and costs you $6 with probability 6/36. What is your approximate probability of losing money in one play of the game?
A) 0
B) 0.167
C) 0.444
D) 0.500
E) 0.556
A) 0
B) 0.167
C) 0.444
D) 0.500
E) 0.556

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
9
Only 20 of a sample of 275 students say they are vegetarians. Of these, nine eat both milk products and eggs (lacto-ovo vegetarians), three eat eggs but not milk products, and eight eat neither (vegans.) If we choose one of those 275 students at random and the chosen student turns out to be a vegetarian, what is the probability that the chosen student eats neither milk products nor eggs?
A) 8/275
B) 20/275
C) 8/20
D) 0.5
E) 1
A) 8/275
B) 20/275
C) 8/20
D) 0.5
E) 1

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
10
In many popular board games, a player rolls two dice and moves the number of spaces equal to the sum shown on the dice. Here is the assignment of probabilities to the sum of the numbers on the up faces when two fair dice are rolled: 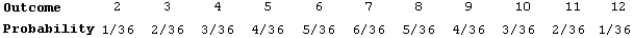 Suppose Scott and Jennifer each rolls a sum of 9 on their first rolls. What is the probability that Quint will have a greater sum on his first roll?
Suppose Scott and Jennifer each rolls a sum of 9 on their first rolls. What is the probability that Quint will have a greater sum on his first roll?
A) 0
B) 1/6
C) 1/12
D) 5/18
E) 1
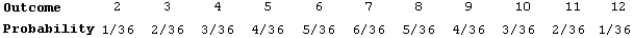 Suppose Scott and Jennifer each rolls a sum of 9 on their first rolls. What is the probability that Quint will have a greater sum on his first roll?
Suppose Scott and Jennifer each rolls a sum of 9 on their first rolls. What is the probability that Quint will have a greater sum on his first roll?A) 0
B) 1/6
C) 1/12
D) 5/18
E) 1

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
11
The _______________ of a statistic indicates what values the statistic takes in repeated samples from the same population and how often it takes those values.
A) formula
B) parameter
C) line graph
D) sampling distribution
E) standard deviation
A) formula
B) parameter
C) line graph
D) sampling distribution
E) standard deviation

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
12
The probability that the sum is 7 when you roll two dice is 1/6; the probability that the sum is 11 is 1/18. Suppose you play a game where you win if the sum is 7 or 11. What is the probability that you win?
A) 2/6
B) 2/18
C) 7/6
D) 2/9
E) 2/24
A) 2/6
B) 2/18
C) 7/6
D) 2/9
E) 2/24

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
13
A friend rolls a cheap 6-sided die many times. He reports that the probabilities of the possible outcomes are about as follows:
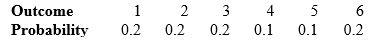
Is this a legitimate assignment of probabilities?
A) Yes.
B) No, the faces must all have the same probability.
C) No, the 3 and 4 faces are opposite each other, so they must have the same probability.
D) No, the total probability for all faces is wrong.
E) No, not all the values given are possible values for a probability.
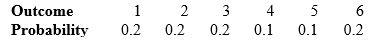
Is this a legitimate assignment of probabilities?
A) Yes.
B) No, the faces must all have the same probability.
C) No, the 3 and 4 faces are opposite each other, so they must have the same probability.
D) No, the total probability for all faces is wrong.
E) No, not all the values given are possible values for a probability.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
14
A household is a group of people living together at the same address. According to the 2015 Current Population Survey's Annual Social and Economic (CPS ASEC) Supplement, if an American household were chosen at random and asked how many people lived there, here are the probabilities:

What is the probability that a randomly chosen household contains four or more people?
A) 0.09
B) 0.14
C) 0.23
D) 0.91
E) It is not possible to tell from the information given.

What is the probability that a randomly chosen household contains four or more people?
A) 0.09
B) 0.14
C) 0.23
D) 0.91
E) It is not possible to tell from the information given.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
15
An experiment has four possible outcomes: A, B, C, and D. Which of the following is a legitimate assignment of probabilities for these four events?
A) 0.3, 0.3, 0.3, 0.3
B) 0.2, 0.4, 0.1, 0.3
C) 0.6, 0.2, 0.3, -0.1
D) 0.2, 0.2, 0.4, 0.4
A) 0.3, 0.3, 0.3, 0.3
B) 0.2, 0.4, 0.1, 0.3
C) 0.6, 0.2, 0.3, -0.1
D) 0.2, 0.2, 0.4, 0.4

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
16
A die has six faces, showing 1 to 6 pips (spots). If a die is balanced, all six faces are equally likely. What must be the probability of each face?
A) 1/10
B) 1/6
C) 1/36
D) Could be any number between 0 and 1.
A) 1/10
B) 1/6
C) 1/36
D) Could be any number between 0 and 1.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
17
A household is a group of people living together at the same address. According to the 2015 Current Population Survey's Annual Social and Economic (CPS ASEC) Supplement, if an American household were chosen at random and asked how many people lived there, here are the probabilities:
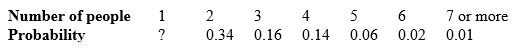
What is the probability that the household chosen contains only one person?
A) 0.52
B) 0.27
C) 0.14
D) 0.73
E) It is not possible to tell from the information given.
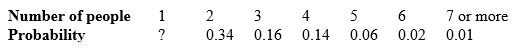
What is the probability that the household chosen contains only one person?
A) 0.52
B) 0.27
C) 0.14
D) 0.73
E) It is not possible to tell from the information given.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose a sorority sells 500 raffle tickets to raise money for a local charity. You purchase 17 of the tickets. If the winning ticket is chosen at random, what is the probability that one of your tickets is chosen as the winning ticket?
A) 0.17
B) 0.017
C) 0.034
D) 0.500
E) 0.002
A) 0.17
B) 0.017
C) 0.034
D) 0.500
E) 0.002

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
19
If we roll a pair of fair dice and count the number of aces (one dot) showing, the probability model is as follows:

The probability of no aces is
A) 0
B) 1/36.
C) 2/3.
D) 25/36.
E) impossible to determine.

The probability of no aces is
A) 0
B) 1/36.
C) 2/3.
D) 25/36.
E) impossible to determine.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
20
A _______________ for a random phenomenon describes all the possible outcomes and indicates how to assign probabilities to any collection of outcomes.
A) standard deviation
B) median
C) probability model
D) boxplot
E) scatterplot
A) standard deviation
B) median
C) probability model
D) boxplot
E) scatterplot

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
21
In backgammon, one rolls a pair of two fair dice. The probability of getting a sum of 7 is
A) 3/36.
B) 4/36.
C) 5/36.
D) 6/36.
E) None of the answers are correct.
A) 3/36.
B) 4/36.
C) 5/36.
D) 6/36.
E) None of the answers are correct.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
22
A grocery chain runs a prize game by giving each customer a ticket that may win a prize when a box is scratched. Printed on the ticket are the following probabilities for a customer who shops once a week:
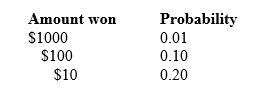
What is the probability of winning nothing?
A) 0.31
B) 0.50
C) 0.69
D) 0.80
E) 0

What is the probability of winning nothing?
A) 0.31
B) 0.50
C) 0.69
D) 0.80
E) 0

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
23
A multiple-choice exam offers five choices for each question. Jason just guesses the answers, so he has probability 1/5 of getting any one answer right. One of your math major friends tells you that the assignment of probabilities to the number of questions Jason gets right out of 10 is (rounded to three decimal places):
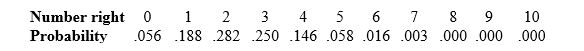
What is the probability that Jason will get no more than two of the ten questions right?
A) 0.244
B) 0.282
C) 0.526
D) 0.718
E) 0.756
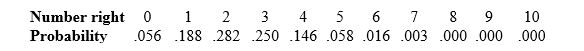
What is the probability that Jason will get no more than two of the ten questions right?
A) 0.244
B) 0.282
C) 0.526
D) 0.718
E) 0.756

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
24
Suppose a sorority is selling 500 raffle tickets to raise money for a local charity. You are going to be the first person to purchase any of the tickets. What is the smallest number of tickets you need to purchase to ensure that your probability of winning is greater than anyone else's probability of winning?
A) 251
B) 250
C) 500
D) 0.5
E) 2
A) 251
B) 250
C) 500
D) 0.5
E) 2

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
25
A household is a group of people living together at the same address. According to the 2015 Current Population Survey's Annual Social and Economic (CPS ASEC) Supplement, if an American household were chosen at random and asked how many people lived there, here are the probabilities:

What is the probability that a randomly chosen household contains 8 people?
A) 0
B) 0.01
C) 0.001
D) 0.99
E) It is not possible to tell from the information given.

What is the probability that a randomly chosen household contains 8 people?
A) 0
B) 0.01
C) 0.001
D) 0.99
E) It is not possible to tell from the information given.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
26
If a ball game of a certain National League Central Division squad were chosen at random, here is the probability distribution for the number of hits per game this team's utility infielder would have had:
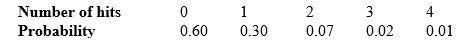
In the randomly chosen game, the probability that the utility infielder has three or more hits is:
A) 0.99.
B) 0.97.
C) 0.02.
D) 0.03.
E) 0.01.
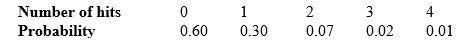
In the randomly chosen game, the probability that the utility infielder has three or more hits is:
A) 0.99.
B) 0.97.
C) 0.02.
D) 0.03.
E) 0.01.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
27
If a woman of 25 years of age or over were chosen at random from the entire U.S. population, here are the probabilities for her highest level of educational attainment:

To make this a legitimate assignment of probabilities, the probability that the woman chosen has less than a high school diploma as her highest level of educational attainment must be:
A)1)
B) 0.8.
C) 0.12.
D) -0.12.
E) 0.

To make this a legitimate assignment of probabilities, the probability that the woman chosen has less than a high school diploma as her highest level of educational attainment must be:
A)1)
B) 0.8.
C) 0.12.
D) -0.12.
E) 0.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
28
A psychologist thinks that listening to Bach helps people think. She gives subjects a set of puzzles and measures how many they solve in five minutes while listening to Bach. From data on many people, the psychologist gets this probability model:
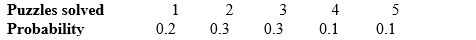
The probability that a subject solves more than one puzzle is
A) 0.2.
B) 0.8.
C) 2.3.
D)
1)E)
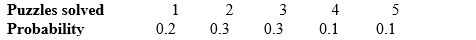
The probability that a subject solves more than one puzzle is
A) 0.2.
B) 0.8.
C) 2.3.
D)
1)E)

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
29
For a certain random experiment, let's consider four different outcomes, which we'll call A, B, C, and D. It has been determined that the probabilities of these outcomes are as follows:
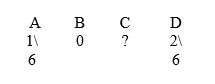
What is the probability of outcome C?
A) 0.75
B) 0.50
C) 0.25
D) 0
E) There is a mistake in the table, because a probability cannot be 0.
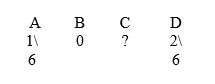
What is the probability of outcome C?
A) 0.75
B) 0.50
C) 0.25
D) 0
E) There is a mistake in the table, because a probability cannot be 0.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
30
When you choose a card at random from a well-shuffled deck, the probability is 1/4 that your card belongs to any one of the four suits: clubs, diamonds, hearts, and spades. Clubs and spades are black, hearts and diamonds are red. The probability that your randomly chosen card is red is
A)0)
B) 1/4.
C) 1/2.
D) 3/4.
E) 1.
A)0)
B) 1/4.
C) 1/2.
D) 3/4.
E) 1.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck


