Deck 11: Taylor Polynomials and Infinite Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/132
Play
Full screen (f)
Deck 11: Taylor Polynomials and Infinite Series
1
Is this the graph of y = 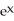 and are its first two Taylor polynomials at x = 0 on the same axis?
and are its first two Taylor polynomials at x = 0 on the same axis? 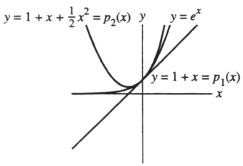
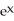 and are its first two Taylor polynomials at x = 0 on the same axis?
and are its first two Taylor polynomials at x = 0 on the same axis? 
True
2
Write down the fourth Taylor polynomial of f(x) = 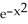 at x = 0.
at x = 0.
Enter your answer an an unlabeled polynomial in x in standard Taylor polynomial form (i.e., constant first, highest power last ).
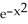 at x = 0.
at x = 0.Enter your answer an an unlabeled polynomial in x in standard Taylor polynomial form (i.e., constant first, highest power last ).
1 - 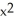 +
+ 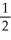
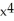
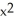 +
+ 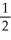
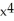
3
Suppose f(x) = 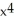 - 7
- 7 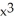 + 2. The fifth Taylor polynomial of f(x) at x = 0 is
+ 2. The fifth Taylor polynomial of f(x) at x = 0 is 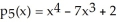 .
.
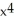 - 7
- 7 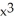 + 2. The fifth Taylor polynomial of f(x) at x = 0 is
+ 2. The fifth Taylor polynomial of f(x) at x = 0 is 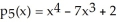 .
.True
4
Let f(x) = 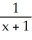 . Determine the second Taylor polynomial
. Determine the second Taylor polynomial 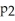 (x) of f(x) at x = 0.
(x) of f(x) at x = 0.
A) 1 - x
B) 1 - 2x + 2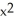
C) 1 - x -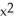
D) 1 - x +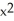
E) none of these
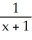 . Determine the second Taylor polynomial
. Determine the second Taylor polynomial  (x) of f(x) at x = 0.
(x) of f(x) at x = 0.A) 1 - x
B) 1 - 2x + 2
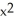
C) 1 - x -
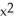
D) 1 - x +
E) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
5
Find the third Taylor polynomial of f(x) = 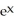 at x = 0 and use it to approximate e.
at x = 0 and use it to approximate e.
Enter just a reduced fraction of form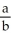 .
.
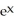 at x = 0 and use it to approximate e.
at x = 0 and use it to approximate e.Enter just a reduced fraction of form
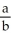 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose f(x) = 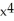 - 7
- 7 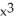 + 2. The third Taylor polynomial of f(x) at x = 0 is
+ 2. The third Taylor polynomial of f(x) at x = 0 is 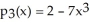 .
.
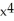 - 7
- 7 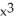 + 2. The third Taylor polynomial of f(x) at x = 0 is
+ 2. The third Taylor polynomial of f(x) at x = 0 is 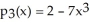 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
7
Let f(x) = ln(1 + x). Determine the third Taylor polynomial of f(x) at x = 0.
A) x +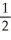
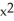 +
+ 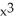
B) x +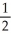
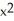 +
+ 
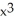
C) x -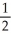
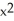 +
+ 
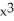
D) x +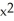 +
+ 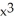
A) x +
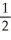
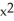 +
+ 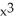
B) x +
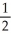
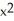 +
+ 
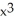
C) x -
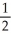
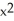 +
+ 
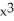
D) x +
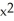 +
+ 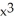

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
8
Find the third Taylor polynomial of f(x) = sin x at x = 0 and use it to approximate 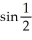 .
.
Enter just a real number rounded off to two decimal places.
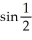 .
.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
9
Find the second Taylor polynomial for f(x) = 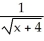 at x = 0 and use it to approximate
at x = 0 and use it to approximate 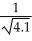 .
.
Enter just a real number rounded off to two decimal places.
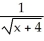 at x = 0 and use it to approximate
at x = 0 and use it to approximate 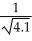 .
.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
10
Estimate 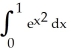 by using the second Taylor polynomial for f(x) =
by using the second Taylor polynomial for f(x) = 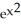 . Is
. Is 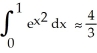 the solution?
the solution?
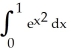 by using the second Taylor polynomial for f(x) =
by using the second Taylor polynomial for f(x) = 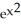 . Is
. Is 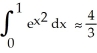 the solution?
the solution?
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
11
If f(x) = 2 + 3x - 2 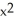 + 2
+ 2 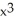 , then what i f'''(0)?
, then what i f'''(0)?
Enter just an integer.
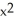 + 2
+ 2 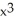 , then what i f'''(0)?
, then what i f'''(0)?Enter just an integer.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
12
The function f(x) = sin 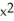 is approximated by its second Taylor polynomial
is approximated by its second Taylor polynomial 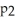 (x) at x = 0. Which of the following statements is NOT true?
(x) at x = 0. Which of the following statements is NOT true?
A) f'(0) = 0
B)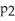 (x) =
(x) =  +
+ 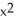
C)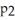 (x) =
(x) = 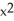
D) f''(0) = 2
E) none of these
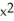 is approximated by its second Taylor polynomial
is approximated by its second Taylor polynomial 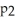 (x) at x = 0. Which of the following statements is NOT true?
(x) at x = 0. Which of the following statements is NOT true?A) f'(0) = 0
B)
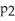 (x) =
(x) =  +
+ 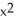
C)
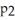 (x) =
(x) = 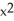
D) f''(0) = 2
E) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
13
Let f(x) = 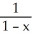 . Determine the fourth Taylor polynomial at x = 0.
. Determine the fourth Taylor polynomial at x = 0.
A) 1 + x +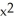 +
+ 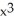 +
+ 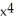
B) 1 + x + 2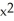 +
+ 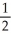
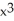 +
+ 
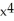
C) 1 - x +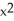 -
- 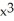 +
+ 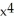
D) 1 - x + 2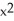 -
- 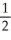
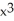 +
+ 
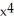
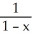 . Determine the fourth Taylor polynomial at x = 0.
. Determine the fourth Taylor polynomial at x = 0.A) 1 + x +
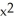 +
+ 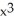 +
+ 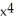
B) 1 + x + 2
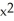 +
+ 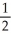
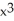 +
+ 
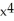
C) 1 - x +
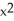 -
- 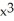 +
+ 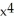
D) 1 - x + 2
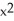 -
- 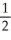
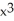 +
+ 
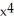

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
14
Determine the second Taylor polynomial of sin 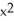 at x = 0.
at x = 0.
Enter an unlabeled polynomial in x in standard form (i.e., highest powers first).
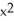 at x = 0.
at x = 0.Enter an unlabeled polynomial in x in standard form (i.e., highest powers first).

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
15
Find the third Taylor polynomial of f(x) = 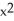 + sin x at x = 0.
+ sin x at x = 0.
Enter an unlabeled polynomial in x in standard form (i.e., highest powers first).
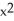 + sin x at x = 0.
+ sin x at x = 0.Enter an unlabeled polynomial in x in standard form (i.e., highest powers first).

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
16
Find the second Taylor polynomial of f(x) = sin 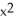 at x = 0 and use it to approximate the area under the curve f(x) between 0 and
at x = 0 and use it to approximate the area under the curve f(x) between 0 and 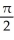 .
.
Enter an unlabeled polynomial in x in standard form followed by a comma and then just a quotient representing the area (π in the numerator).
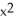 at x = 0 and use it to approximate the area under the curve f(x) between 0 and
at x = 0 and use it to approximate the area under the curve f(x) between 0 and 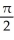 .
.Enter an unlabeled polynomial in x in standard form followed by a comma and then just a quotient representing the area (π in the numerator).

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
17
Determine the third Taylor polynomial of f(x) = 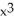 - 3x at x = 0.
- 3x at x = 0.
Enter an unlabeled polynomial in x in standard form (i.e., highest powers first).
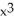 - 3x at x = 0.
- 3x at x = 0.Enter an unlabeled polynomial in x in standard form (i.e., highest powers first).

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
18
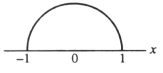
The area of a circle with radius 1 is π. If f(x) = 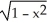 gives the top half of this circle, as illustrated below, use the second Taylor polynomial of f(x) at x = 0 to find an approximate value for π. Is the following correct?
gives the top half of this circle, as illustrated below, use the second Taylor polynomial of f(x) at x = 0 to find an approximate value for π. Is the following correct? 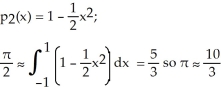
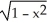 gives the top half of this circle, as illustrated below, use the second Taylor polynomial of f(x) at x = 0 to find an approximate value for π. Is the following correct?
gives the top half of this circle, as illustrated below, use the second Taylor polynomial of f(x) at x = 0 to find an approximate value for π. Is the following correct? 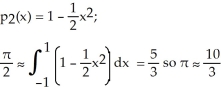


Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
19
Let f(x) =  - 4x - 1. Which of the following statements is true? (All Taylor polynomials are at x = 0.)
- 4x - 1. Which of the following statements is true? (All Taylor polynomials are at x = 0.)
A) (-1) = 0
(-1) = 0
B) (1) = 7
(1) = 7
C) = f(x) for all n ≥ 3
= f(x) for all n ≥ 3
D) (3) = -11
(3) = -11
E) none of these
 - 4x - 1. Which of the following statements is true? (All Taylor polynomials are at x = 0.)
- 4x - 1. Which of the following statements is true? (All Taylor polynomials are at x = 0.)A)
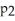 (-1) = 0
(-1) = 0B)
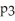 (1) = 7
(1) = 7C)
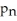 = f(x) for all n ≥ 3
= f(x) for all n ≥ 3D)
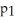 (3) = -11
(3) = -11E) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
20
Determine the third Taylor polynomial of f(x) = 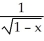 at x = 0.
at x = 0.
Enter your answer as an unlabeled polynomial in x in standard form (i.e., highest powers first).
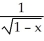 at x = 0.
at x = 0.Enter your answer as an unlabeled polynomial in x in standard form (i.e., highest powers first).

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose f(x) = 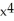 - 7
- 7 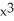 + 2. The fifth Taylor polynomial of f(x) at x = 1 is
+ 2. The fifth Taylor polynomial of f(x) at x = 1 is 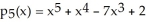 .
.
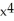 - 7
- 7 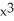 + 2. The fifth Taylor polynomial of f(x) at x = 1 is
+ 2. The fifth Taylor polynomial of f(x) at x = 1 is 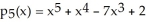 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
22
Find the third Taylor polynomial of f(x) = cos x at x = 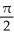 .
.
Enter your answer as an unlabeled polynomial in x -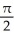 in standard form (i.e., highest powers first).
in standard form (i.e., highest powers first).
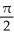 .
.Enter your answer as an unlabeled polynomial in x -
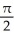 in standard form (i.e., highest powers first).
in standard form (i.e., highest powers first).
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose f(0) = 1, f'(0) = 1, and f''(0) = -1. Use a Taylor polynomial of degree two to approximate f 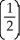 . Is
. Is 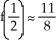 the solution?
the solution?
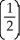 . Is
. Is 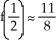 the solution?
the solution?
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
24
The Newton-Raphson algorithm is applied to estimate 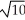 . If
. If 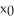 = 3, find
= 3, find 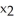 .
.
A)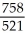
B)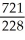
C)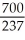
D)
E) none of these
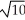 . If
. If 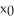 = 3, find
= 3, find 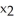 .
.A)
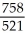
B)
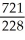
C)
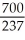
D)

E) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
25
Suppose the second Taylor polynomial for f(x) at x = 3 is 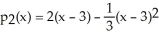 . Find f''(3).
. Find f''(3).
Enter just a reduced fraction.
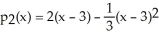 . Find f''(3).
. Find f''(3).Enter just a reduced fraction.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose f(x) = 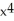 - 7
- 7 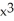 + 2. The third Taylor polynomial of f(x) at x = 1 is
+ 2. The third Taylor polynomial of f(x) at x = 1 is 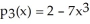 .
.
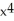 - 7
- 7 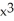 + 2. The third Taylor polynomial of f(x) at x = 1 is
+ 2. The third Taylor polynomial of f(x) at x = 1 is 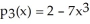 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
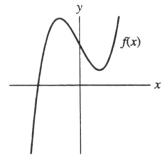
27
If the following is a graph of f(x), which of the following could be the first Taylor polynomial of f at 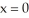 ?
? 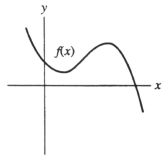
A)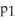 (x) = 2 + 2x
(x) = 2 + 2x
B)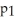 (x) = 2 - 2x
(x) = 2 - 2x
C)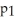 (x) = 2x - 2
(x) = 2x - 2
D)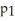 (x) = 2x + 5
(x) = 2x + 5
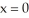 ?
? 
A)
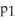 (x) = 2 + 2x
(x) = 2 + 2xB)
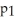 (x) = 2 - 2x
(x) = 2 - 2xC)
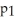 (x) = 2x - 2
(x) = 2x - 2D)
 (x) = 2x + 5
(x) = 2x + 5
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
28
Determine the third Taylor polynomial of f(x) = 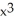 - 2x + 4 at x = 1.
- 2x + 4 at x = 1.
Enter an unlabeled polynomial in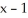 in standard form (i.e., highest powers first).
in standard form (i.e., highest powers first).
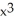 - 2x + 4 at x = 1.
- 2x + 4 at x = 1.Enter an unlabeled polynomial in
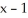 in standard form (i.e., highest powers first).
in standard form (i.e., highest powers first).
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
29
Use the second Taylor polynomial at x = 1 to estimate 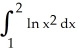 .
.
Enter just a reduced fraction.
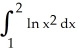 .
.Enter just a reduced fraction.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose that the first Taylor polynomial of a function f(x) at x = 0 is 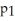 (x) = 2 - 3x. Which of the following could be a graph of f(x) ?
(x) = 2 - 3x. Which of the following could be a graph of f(x) ?
A)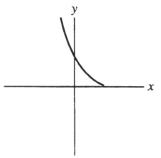
B)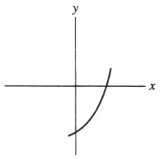
C)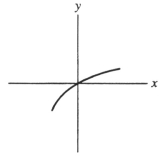
D)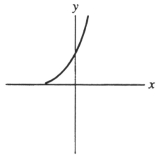
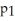 (x) = 2 - 3x. Which of the following could be a graph of f(x) ?
(x) = 2 - 3x. Which of the following could be a graph of f(x) ?A)

B)

C)

D)


Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
31
Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate ![Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate [Hint: .] Enter your answer as an unlabeled polynomial in in standard form :](https://storage.examlex.com/TB3874/11ea9846_6936_72a1_b1f1_b72e4cefea87_TB3874_11.jpg) [Hint:
[Hint: ![Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate [Hint: .] Enter your answer as an unlabeled polynomial in in standard form :](https://storage.examlex.com/TB3874/11ea9846_6936_72a2_b1f1_9d71ffff1eb7_TB3874_11.jpg) .]
.]
Enter your answer as an unlabeled polynomial in![Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate [Hint: .] Enter your answer as an unlabeled polynomial in in standard form :](https://storage.examlex.com/TB3874/11ea9846_6936_99b3_b1f1_6f399cd92351_TB3874_11.jpg) in standard form :
in standard form : ![Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate [Hint: .] Enter your answer as an unlabeled polynomial in in standard form :](https://storage.examlex.com/TB3874/11ea9846_6936_99b4_b1f1_29313b7130b9_TB3874_11.jpg)
![Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate [Hint: .] Enter your answer as an unlabeled polynomial in in standard form :](https://storage.examlex.com/TB3874/11ea9846_6936_72a1_b1f1_b72e4cefea87_TB3874_11.jpg) [Hint:
[Hint: ![Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate [Hint: .] Enter your answer as an unlabeled polynomial in in standard form :](https://storage.examlex.com/TB3874/11ea9846_6936_72a2_b1f1_9d71ffff1eb7_TB3874_11.jpg) .]
.]Enter your answer as an unlabeled polynomial in
![Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate [Hint: .] Enter your answer as an unlabeled polynomial in in standard form :](https://storage.examlex.com/TB3874/11ea9846_6936_99b3_b1f1_6f399cd92351_TB3874_11.jpg) in standard form :
in standard form : ![Determine the third Taylor polynomial of f(x) = ln(2 - x) at x = 1 and use it to estimate [Hint: .] Enter your answer as an unlabeled polynomial in in standard form :](https://storage.examlex.com/TB3874/11ea9846_6936_99b4_b1f1_29313b7130b9_TB3874_11.jpg)

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
32
Below is a graph of the function f(x). Which of the following could be the first Taylor polynomial of f(x) at 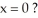
A)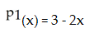
B)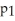 (x) = -2 - 3x
(x) = -2 - 3x
C)
D)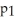 (x) = 3 + 4x
(x) = 3 + 4x
E) none of these
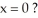

A)
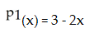
B)
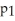 (x) = -2 - 3x
(x) = -2 - 3xC)
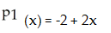
D)
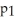 (x) = 3 + 4x
(x) = 3 + 4xE) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
33
The Newton-Raphson algorithm is used to approximate the zero of f(x) = 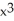 + x - 5 between x = 1 and x=2 . If x0 = 1, find x1.
+ x - 5 between x = 1 and x=2 . If x0 = 1, find x1.
A) 7/4
B) 1/4
C) 3/4
D) 7/3
E) none of these
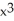 + x - 5 between x = 1 and x=2 . If x0 = 1, find x1.
+ x - 5 between x = 1 and x=2 . If x0 = 1, find x1.A) 7/4
B) 1/4
C) 3/4
D) 7/3
E) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
34
If f(x) = 1 - 3(x - 2) + 4 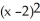 + 6
+ 6 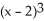 , then what is f''(2)? Enter just an integer.
, then what is f''(2)? Enter just an integer.
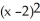 + 6
+ 6 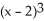 , then what is f''(2)? Enter just an integer.
, then what is f''(2)? Enter just an integer.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
35
Find the second Taylor polynomial of f(x) = 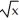 at x = 9 and use it to approximate
at x = 9 and use it to approximate 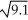 .
.
Enter just a real number rounded off to two decimal places.
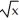 at x = 9 and use it to approximate
at x = 9 and use it to approximate 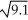 .
.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
36
Below is a graph of function f(x). Which of the following could be the second Taylor polynomial of f(x) at 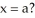
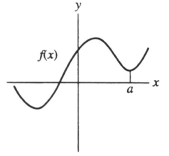
A)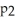 (x) =
(x) = 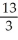 +
+  (x - a)
(x - a)
B)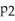 (x) =
(x) = 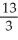 +
+ 
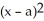
C)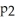 (x) =
(x) =  -
- 
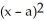
D)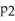 (x) =
(x) = 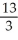 -
-  (x - a) +
(x - a) + 
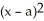
E)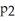 (x) =
(x) =  (x - a) -
(x - a) - 
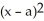
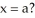

A)
 (x) =
(x) = 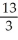 +
+  (x - a)
(x - a)B)
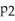 (x) =
(x) = 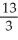 +
+ 
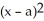
C)
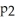 (x) =
(x) = 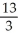 -
- 
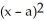
D)
 (x) =
(x) = 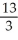 -
-  (x - a) +
(x - a) + 
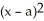
E)
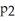 (x) =
(x) =  (x - a) -
(x - a) - 

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
37
Let f(x) = 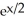 . Determine the second Taylor polynomial of f(x) at x = 2.
. Determine the second Taylor polynomial of f(x) at x = 2.
A) 1 +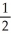 (x - 2) +
(x - 2) + 
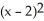
B) 1 -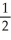 (x - 2) +
(x - 2) + 
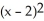
C) 1 +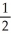 (x - 2) +
(x - 2) + 
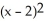
D) e +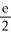 (x - 2) +
(x - 2) + 
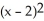
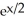 . Determine the second Taylor polynomial of f(x) at x = 2.
. Determine the second Taylor polynomial of f(x) at x = 2.A) 1 +
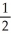 (x - 2) +
(x - 2) + 
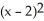
B) 1 -
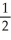 (x - 2) +
(x - 2) + 
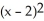
C) 1 +
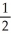 (x - 2) +
(x - 2) + 
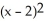
D) e +
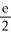 (x - 2) +
(x - 2) + 
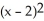

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
38
The Newton-Raphson algorithm is applied to estimate a zero of f(x) with 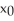 = 3. Which of the following statements is true?
= 3. Which of the following statements is true?
A)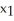 = 3 -
= 3 - 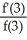
B) = 3 +
= 3 + 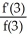
C) = 3 -
= 3 - 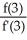
D)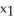 =
= 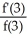
E) none of these
 = 3. Which of the following statements is true?
= 3. Which of the following statements is true?A)
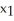 = 3 -
= 3 - 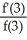
B)
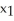 = 3 +
= 3 + 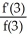
C)
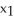 = 3 -
= 3 - 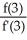
D)
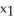 =
= 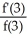
E) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
39
Let f(x) = ln x. Find the second Taylor polynomial of f(x) at x = 2.
A) 1 +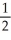 (x - 2) +
(x - 2) + 
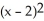
B) ln 2 -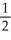 (x - 2) -
(x - 2) - 
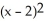
C) 1 +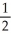 (x - 2) -
(x - 2) - 
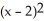
D) ln 2 +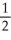 (x - 2) -
(x - 2) - 
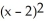
A) 1 +
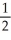 (x - 2) +
(x - 2) + 
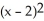
B) ln 2 -
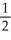 (x - 2) -
(x - 2) - 
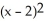
C) 1 +
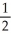 (x - 2) -
(x - 2) - 
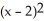
D) ln 2 +
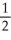 (x - 2) -
(x - 2) - 

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
40
A polynomial f(x) of degree 3 for which f(1) = -1, f'(1) = 2, f''(1) = -1, and f'''(1) = -2 is given by
A) f(x) = -1 + 2(x - 1) -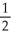
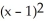 -
- 
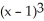
B) f(x) = -1 + 2(x - 1) - 1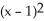 - 2
- 2 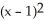
C) f(x) = -1 + 2x -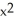 - 2
- 2 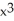
D) f(x) =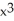 - 2
- 2 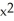 - 3x + 2
- 3x + 2
E) none of these
A) f(x) = -1 + 2(x - 1) -
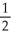
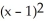 -
- 
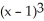
B) f(x) = -1 + 2(x - 1) - 1
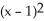 - 2
- 2 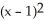
C) f(x) = -1 + 2x -
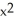 - 2
- 2 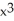
D) f(x) =
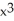 - 2
- 2 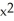 - 3x + 2
- 3x + 2E) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
41
f(x) = 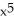 + x - 3 has a zero between 1 and 2 .
+ x - 3 has a zero between 1 and 2 .
Use two repetitions of the Newton-Raphson algorithm to approximate this zero with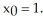 Enter just a real number rounded off to two decimal places.
Enter just a real number rounded off to two decimal places.
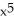 + x - 3 has a zero between 1 and 2 .
+ x - 3 has a zero between 1 and 2 .Use two repetitions of the Newton-Raphson algorithm to approximate this zero with
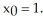 Enter just a real number rounded off to two decimal places.
Enter just a real number rounded off to two decimal places.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
42
Below is a graph of the functions h(x) and g(x). In using the Newton-Raphson algorithm to find where  , which of the following statements is false?
, which of the following statements is false? 
A)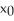 = 3 could be used as the initial approximation.
= 3 could be used as the initial approximation.
B) Use the Newton-Raphson algorithm to find the zeroes of f(x) = h(x) - g(x).
C) Use the Newton-Raphson algorithm to find the zeroes of f(x) = h(x) + g(x).
D)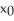 = 4 could be used as the initial approximation.
= 4 could be used as the initial approximation.
E) Use the Newton-Raphson algorithm to find the zeroes of f(x) = g(x) - h(x).
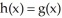 , which of the following statements is false?
, which of the following statements is false? 
A)
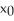 = 3 could be used as the initial approximation.
= 3 could be used as the initial approximation.B) Use the Newton-Raphson algorithm to find the zeroes of f(x) = h(x) - g(x).
C) Use the Newton-Raphson algorithm to find the zeroes of f(x) = h(x) + g(x).
D)
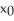 = 4 could be used as the initial approximation.
= 4 could be used as the initial approximation.E) Use the Newton-Raphson algorithm to find the zeroes of f(x) = g(x) - h(x).

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
43
Use two repetitions of the Newton-Raphson algorithm to approximate the zero of f(x) = sin x - cos x near x = 0.
Enter just a real number rounded off to two decimal places.
Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
44
Determine the sum of the series 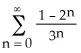 .
.
A) -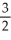
B) 3
C)
D) none of these
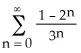 .
.A) -
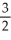
B) 3
C)

D) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
45
Use three repetitions of the Newton-Raphson algorithm to approximate 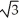 . Let
. Let 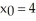 .
.
Enter just a real number rounded off to two decimal places.
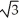 . Let
. Let 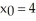 .
.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
46
Use the Newton-Raphson algorithm with three repetitions to approximate the solution to 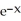 = 2 - x near x = 2.
= 2 - x near x = 2.
Enter just a real number rounded off to two decimal places.
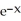 = 2 - x near x = 2.
= 2 - x near x = 2.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
47
Use the Newton-Raphson algorithm with three repetitions to approximate the zero of f(x) = 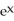 - 2 near
- 2 near 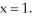 Enter just a real number rounded off to two decimal places.
Enter just a real number rounded off to two decimal places.
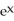 - 2 near
- 2 near 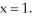 Enter just a real number rounded off to two decimal places.
Enter just a real number rounded off to two decimal places.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
48
Use the Newton-Raphson algorithm with three repetitions to approximate the zero of 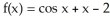 near
near 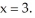 Enter just a real number rounded off to two decimal places.
Enter just a real number rounded off to two decimal places.
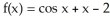 near
near 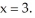 Enter just a real number rounded off to two decimal places.
Enter just a real number rounded off to two decimal places.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
49
Use two repetitions of the Newton-Raphson algorithm to find the value of x near zero for which 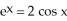 .
.
Enter just a real number rounded off to two decimal places.
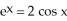 .
.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
50
Below is a graph of the function f(x). If 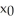 is taken as the initial approximation of the zero of f(x), then which of the following points, A, B, C, or D could be given by the Newton-Raphson algorithm as the next approximation?
is taken as the initial approximation of the zero of f(x), then which of the following points, A, B, C, or D could be given by the Newton-Raphson algorithm as the next approximation? 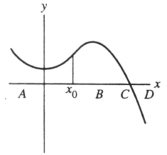
A) A
B) B
C) C
D) D
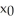 is taken as the initial approximation of the zero of f(x), then which of the following points, A, B, C, or D could be given by the Newton-Raphson algorithm as the next approximation?
is taken as the initial approximation of the zero of f(x), then which of the following points, A, B, C, or D could be given by the Newton-Raphson algorithm as the next approximation? 
A) A
B) B
C) C
D) D

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
51
Let 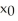 = 2. Use three repetitions of the Newton-Raphson algorithm to approximate
= 2. Use three repetitions of the Newton-Raphson algorithm to approximate 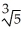 .
.
Enter just a real number rounded off to two decimal places (no label).
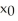 = 2. Use three repetitions of the Newton-Raphson algorithm to approximate
= 2. Use three repetitions of the Newton-Raphson algorithm to approximate 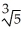 .
.Enter just a real number rounded off to two decimal places (no label).

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
52
Use two repetitions of the Newton-Raphson algorithm to find the value of x near zero for which 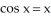 .
.
Enter just a real number rounded off to two decimal places.
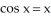 .
.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
53
Determine the sum of the series 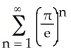 .
.
A)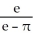
B)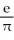
C)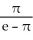
D) none of these
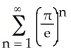 .
.A)
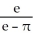
B)
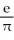
C)
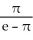
D) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
54
Determine the sum of the series 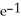 +
+ 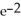 +
+ 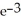 + ... if it converges.
+ ... if it converges.
A) diverges
B)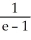
C)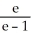
D) e
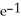 +
+ 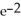 +
+ 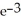 + ... if it converges.
+ ... if it converges.A) diverges
B)
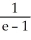
C)
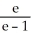
D) e

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose 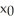 is an initial approximation of a zero of the function f(x). Using the Newton-Raphson algorithm, a second approximation,
is an initial approximation of a zero of the function f(x). Using the Newton-Raphson algorithm, a second approximation, 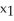 is obtained. Which of the following must be true?
is obtained. Which of the following must be true?
A)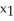 is the x-coordinate of the x-intercept of the tangent line to f(x) at
is the x-coordinate of the x-intercept of the tangent line to f(x) at 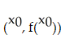
B) f(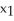 ) = 0
) = 0
C)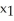 =
= 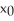 -
- 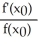
D)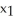 is closer to the zero of f(x) than
is closer to the zero of f(x) than 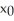 .
.
E) all of these
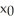 is an initial approximation of a zero of the function f(x). Using the Newton-Raphson algorithm, a second approximation,
is an initial approximation of a zero of the function f(x). Using the Newton-Raphson algorithm, a second approximation, 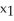 is obtained. Which of the following must be true?
is obtained. Which of the following must be true?A)
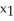 is the x-coordinate of the x-intercept of the tangent line to f(x) at
is the x-coordinate of the x-intercept of the tangent line to f(x) at 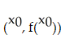
B) f(
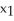 ) = 0
) = 0C)
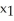 =
= 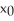 -
- 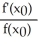
D)
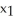 is closer to the zero of f(x) than
is closer to the zero of f(x) than 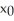 .
.E) all of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
56
Determine the sum of the series 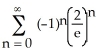 .
.
A)
B)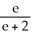
C) 1 -
D) none of these
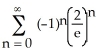 .
.A)

B)
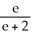
C) 1 -

D) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
57
Use two repetitions of the Newton-Raphson algorithm to approximate 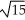 .
.
Enter just a real number rounded off to two decimal places.
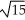 .
.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
58
Determine the sum of the series 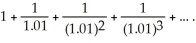
A) 101
B)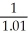
C) 10.1
D) none of these
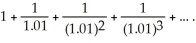
A) 101
B)
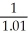
C) 10.1
D) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
59
Use two repetitions of the Newton-Raphson algorithm to approximate the value of x for which 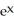 = 3x. Use
= 3x. Use 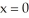 as the first approximation.
as the first approximation.
Enter just a real number rounded off to two decimal places.
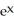 = 3x. Use
= 3x. Use 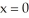 as the first approximation.
as the first approximation.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
60
Use the Newton-Raphson algorithm with two repetitions to estimate the positive solution of sin x = 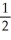 x. Use
x. Use 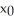 = 2.
= 2.
Enter just a real number rounded off to two decimal places.
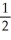 x. Use
x. Use 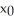 = 2.
= 2.Enter just a real number rounded off to two decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
61
Sum an appropriate infinite series to find the rational number whose decimal expansion is: 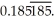 Enter just a reduced fraction of form
Enter just a reduced fraction of form 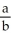 .
.
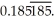 Enter just a reduced fraction of form
Enter just a reduced fraction of form 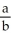 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
62
Determine the sum of the following geometric series: 1 - 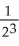 +
+ 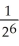 -
- 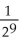 +
+ 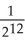 - ... .
- ... .
Enter just a reduced fraction of form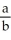 .
.
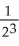 +
+ 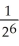 -
- 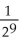 +
+ 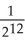 - ... .
- ... .Enter just a reduced fraction of form
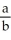 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
63
Sum an appropriate infinite series to find the rational number whose decimal expansion is: 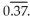 Enter just a reduced fraction of form
Enter just a reduced fraction of form 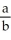 .
.
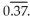 Enter just a reduced fraction of form
Enter just a reduced fraction of form 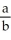 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
64
Determine the sum of the series 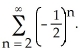
A)
B)
C)
D) none of these
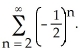
A)

B)

C)

D) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
65
Determine the sum of the series 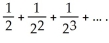
A) 2
B) 1
C)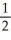
D) none of these
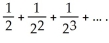
A) 2
B) 1
C)
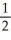
D) none of these

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
66
Determine the sum of the infinite geometric series 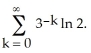 Enter your answer exactly in the reduced form
Enter your answer exactly in the reduced form 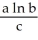 .
.
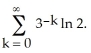 Enter your answer exactly in the reduced form
Enter your answer exactly in the reduced form 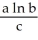 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
67
Determine the sum of the following infinite series: 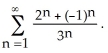 Enter just a reduced fraction of form
Enter just a reduced fraction of form 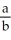 .
.
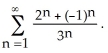 Enter just a reduced fraction of form
Enter just a reduced fraction of form 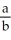 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
68
Sum an appropriate infinite series to find the rational number whose decimal expansion is: 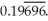 Enter just a reduced fraction of form
Enter just a reduced fraction of form 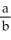 .
.
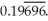 Enter just a reduced fraction of form
Enter just a reduced fraction of form 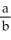 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
69
Determine the sum of the following geometric series: 2 +  +
+  + ... .
+ ... .
Enter just an integer.
 +
+  + ... .
+ ... .Enter just an integer.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
70
Determine the sum of the following infinite series: 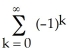
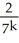 .
.
Enter just a reduced fraction of form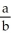 .
.
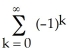
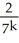 .
.Enter just a reduced fraction of form
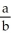 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
71
Determine the sum of the following infinite series: 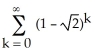 .
.
Enter your answer exactly in the reduced form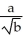 .
.
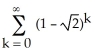 .
.Enter your answer exactly in the reduced form
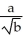 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
72
Determine the sum of the following geometric series: 1 + 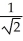 +
+ 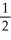 + ... .
+ ... .
Enter your answer exactly in the form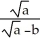 .
.
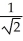 +
+ 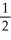 + ... .
+ ... .Enter your answer exactly in the form
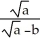 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
73
Determine the sum of the following geometric series: 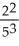 +
+ 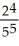 +
+ 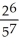 +
+ 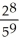 +
+ 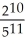 + ... .
+ ... .
Enter just a reduced fraction of form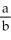 .
.
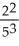 +
+ 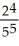 +
+ 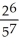 +
+ 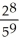 +
+ 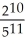 + ... .
+ ... .Enter just a reduced fraction of form
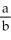 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
74
Determine the sum of the following geometric series: 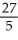 +
+ 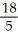 +
+ 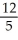 +
+ 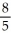 + ... .
+ ... .
Enter a reduced fraction of form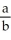 .
.
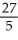 +
+ 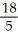 +
+ 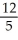 +
+ 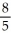 + ... .
+ ... .Enter a reduced fraction of form
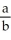 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
75
Determine the sum of the following infinite series: 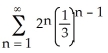 .
.
Enter just an integer.
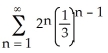 .
.Enter just an integer.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
76
Determine the sum of the following infinite series: 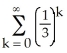
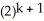 .
.
Enter just an integer.
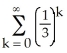
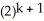 .
.Enter just an integer.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
77
Determine the sum of the following geometric series: 3 - 1.8 + 1.08 + .648 - ... .
Enter just a real number rounded off to three decimal places.
Enter just a real number rounded off to three decimal places.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
78
Sum an appropriate infinite series to find the rational number whose decimal expansion is: 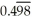 .
.
Enter just a reduced fraction of form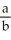 .
.
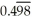 .
.Enter just a reduced fraction of form
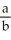 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
79
Determine the sum of the series 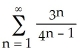 .
.
A)
B) 3
C)
D) 12
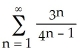 .
.A)

B) 3
C)

D) 12

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
80
Determine the sum of the following geometric series: 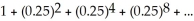 .
.
Enter a reduced fraction of form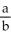 .
.
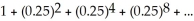 .
.Enter a reduced fraction of form
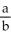 .
.
Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck


