Deck 9: Numerical Solutions of Ordinary Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 9: Numerical Solutions of Ordinary Differential Equations
1
When entering the number 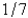 into a three digit base ten calculator, the round-off error is
into a three digit base ten calculator, the round-off error is
A) 0.00143
B) 0.000143
C)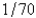
D)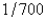
E)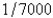
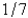 into a three digit base ten calculator, the round-off error is
into a three digit base ten calculator, the round-off error isA) 0.00143
B) 0.000143
C)
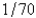
D)
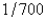
E)
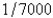
E
2
In the previous problem, the local truncation error in 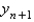 is
is
A)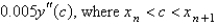
B)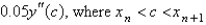
C)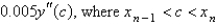
D)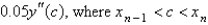
E) unknown
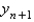 is
isA)
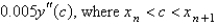
B)
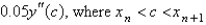
C)
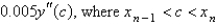
D)
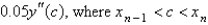
E) unknown
A
3
The improved Euler's method is what type of Runge-Kutta method?
A) first order
B) second order
C) third order
D) fourth order
E) It is not a Runge-Kutta method
A) first order
B) second order
C) third order
D) fourth order
E) It is not a Runge-Kutta method
B
4
The most popular fourth order Runge-Kutta method for the solution of 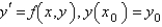 is
is
A)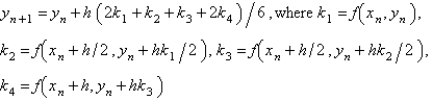
B)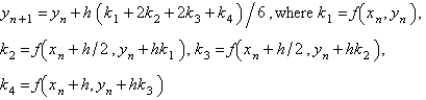
C)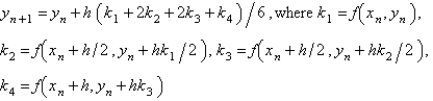
D)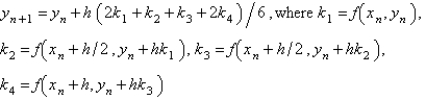
E)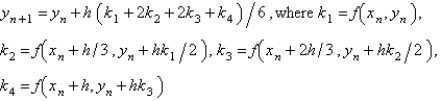
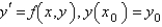 is
isA)
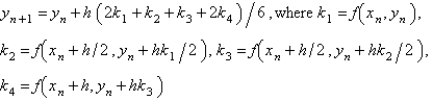
B)
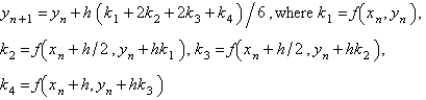
C)
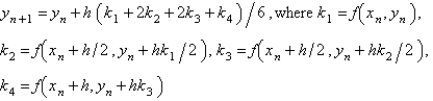
D)
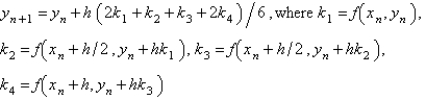
E)
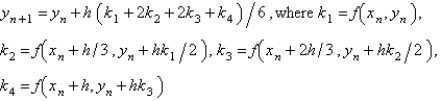

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
The local truncation error for the improved Euler's method is
A)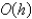
B)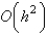
C)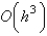
D)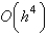
E) unknown
A)
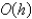
B)
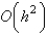
C)
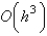
D)
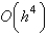
E) unknown

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
The standard central difference approximation of 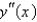 is
is
A)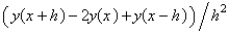
B)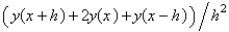
C)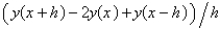
D)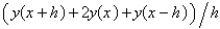
E)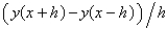
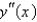 is
isA)
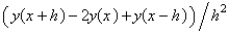
B)
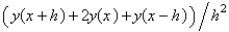
C)
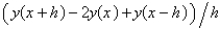
D)
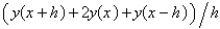
E)
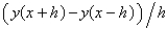

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
Using the Adams-Bashforth-Moulton method from the previous three problems, the solution of 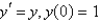 for
for 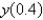 with
with 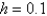 is
is
A) 1.5003
B) 1.4978
C) 1.4919
D) 1.4967
E) none of the above
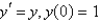 for
for 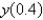 with
with 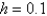 is
isA) 1.5003
B) 1.4978
C) 1.4919
D) 1.4967
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
Using the Adams-Bashforth method from the previous problem, and using the values 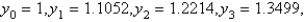 the solution
the solution 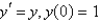 for
for 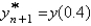 with
with 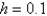 is
is
A) 1.4978
B) 1.5003
C) 1.4919
D) 1.4967
E) none of the above
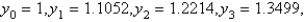 the solution
the solution 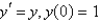 for
for 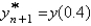 with
with 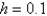 is
isA) 1.4978
B) 1.5003
C) 1.4919
D) 1.4967
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
Using the value of 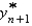 from the previous problem, the Adams-Moulton corrector value for the solution of
from the previous problem, the Adams-Moulton corrector value for the solution of 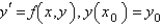 is
is
A)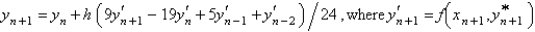
B)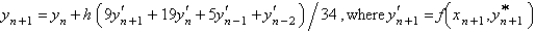
C)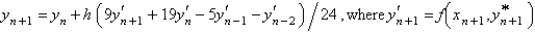
D)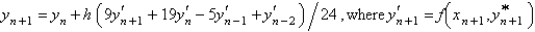
E) none of the above
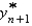 from the previous problem, the Adams-Moulton corrector value for the solution of
from the previous problem, the Adams-Moulton corrector value for the solution of 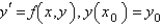 is
isA)
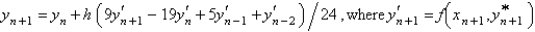
B)
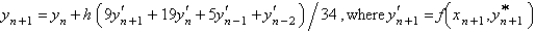
C)
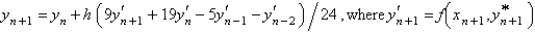
D)
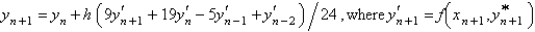
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
The Euler's method solution for 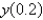 of
of 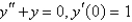 using
using 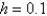 is
is
A) 0.14
B) 0.2
C) 0.21
D) 0.11
E) 0.12
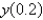 of
of 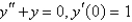 using
using 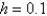 is
isA) 0.14
B) 0.2
C) 0.21
D) 0.11
E) 0.12

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
The Adams-Bashforth formula for finding the solution of 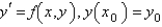 is
is
A)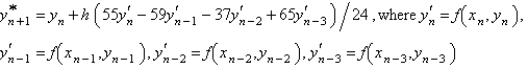
B)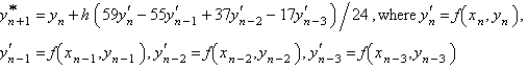
C)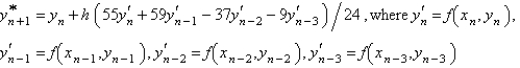
D)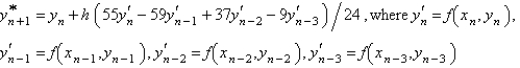
E) none of the above
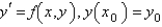 is
isA)
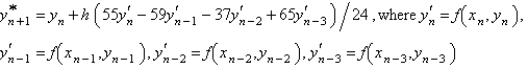
B)
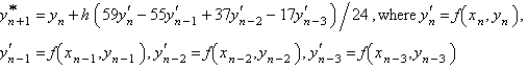
C)
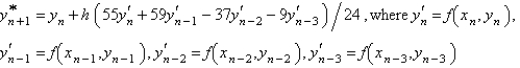
D)
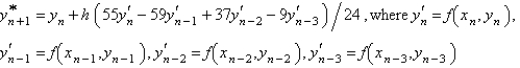
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following are second order Runge-Kutta methods for the solution of 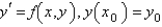 ? Select all that apply.
? Select all that apply.
A)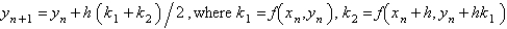
B)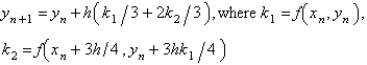
C)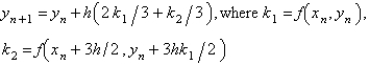
D)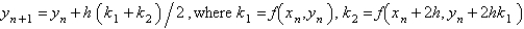
E)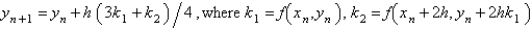
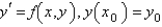 ? Select all that apply.
? Select all that apply.A)
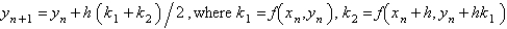
B)
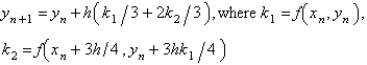
C)
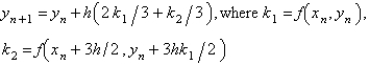
D)
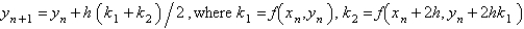
E)
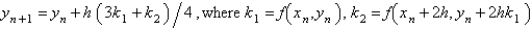

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
The improved Euler's formula for solving 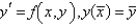 is
is
A)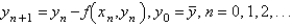
B)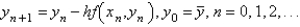
C)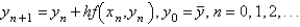
D)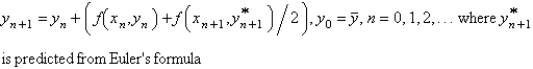
E)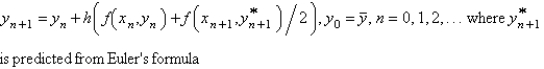
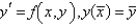 is
isA)
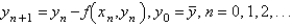
B)
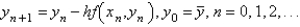
C)
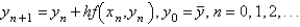
D)
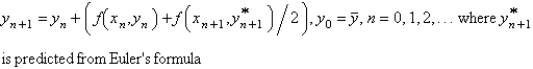
E)
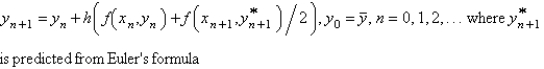

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
The standard backward difference approximation of 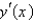 is
is
A)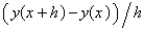
B)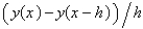
C)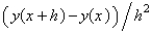
D)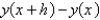
E)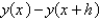
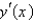 is
isA)
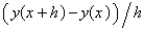
B)
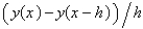
C)
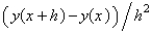
D)
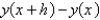
E)
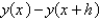

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
The solution of 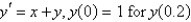 , using the improved Euler's method with
, using the improved Euler's method with 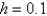 is
is
A) 1.2055
B) 1.21625
C) 1.24205
D) 1.226525
E) 1.235625
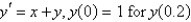 , using the improved Euler's method with
, using the improved Euler's method with 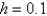 is
isA) 1.2055
B) 1.21625
C) 1.24205
D) 1.226525
E) 1.235625

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
The solution of 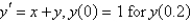 , using Euler's method with
, using Euler's method with 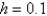 is
is
A) 1.01
B) 1.11
C) 1.21
D) 1.22
E) 1.23
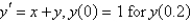 , using Euler's method with
, using Euler's method with 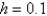 is
isA) 1.01
B) 1.11
C) 1.21
D) 1.22
E) 1.23

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
Using the notation from the text, the finite difference equation for solving the boundary value problem 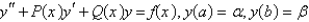 is
is
A)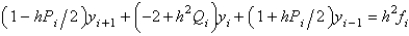
B)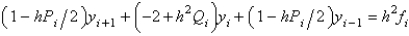
C)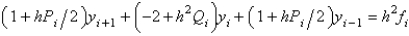
D)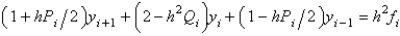
E)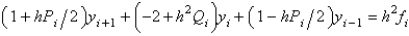
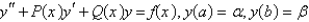 is
isA)
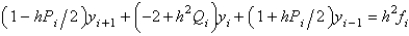
B)
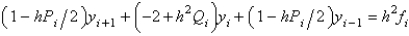
C)
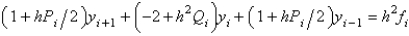
D)
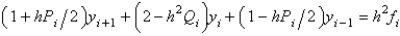
E)
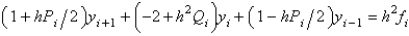

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
Using the method from the previous problem, the solution of 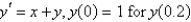 with
with 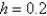 is
is
A) 1.222
B) 1.22
C) 1.2213
D) 1.24
E) 1.21
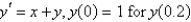 with
with 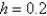 is
isA) 1.222
B) 1.22
C) 1.2213
D) 1.24
E) 1.21

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
Using the method from the previous problem, the solution of 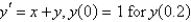 with
with 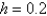 is
is
A) 1.241
B) 1.242
C) 1.2422
D) 1.2426
E) 1.2428
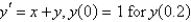 with
with 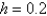 is
isA) 1.241
B) 1.242
C) 1.2422
D) 1.2426
E) 1.2428

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
When entering the number 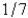 into a three digit base ten calculator, the actual value entered is
into a three digit base ten calculator, the actual value entered is
A)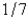
B)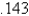
C)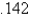
D)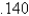
E)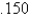
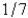 into a three digit base ten calculator, the actual value entered is
into a three digit base ten calculator, the actual value entered isA)
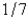
B)
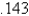
C)
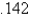
D)
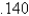
E)
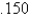

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
The solution of 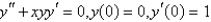 for
for 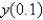 , using the Runge-Kutta method of order four, and using
, using the Runge-Kutta method of order four, and using 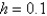 , is
, is
A) 0.0909
B) 0.09999
C) 0.09099
D) 0.09899
E) 0.08899
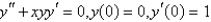 for
for 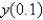 , using the Runge-Kutta method of order four, and using
, using the Runge-Kutta method of order four, and using 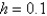 , is
, isA) 0.0909
B) 0.09999
C) 0.09099
D) 0.09899
E) 0.08899

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
Using the method from the previous problem, the solution of 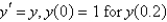 with
with 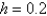 is
is
A) 1.24
B) 1.241
C) 1.214
D) 1.2214
E) 1.224
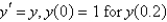 with
with 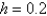 is
isA) 1.24
B) 1.241
C) 1.214
D) 1.2214
E) 1.224

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
The Euler formula for solving the system 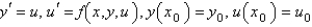 is
is
A)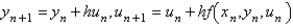
B)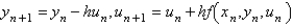
C)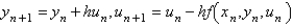
D)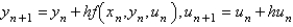
E) none of the above
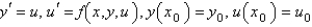 is
isA)
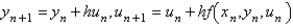
B)
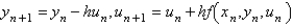
C)
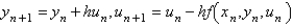
D)
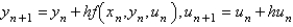
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
A popular second order Runge-Kutta method for the solution of 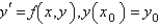 is
is
A)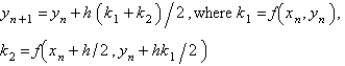
B)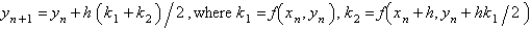
C)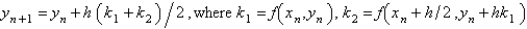
D)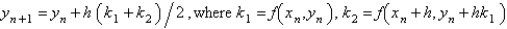
E) none of the above
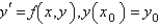 is
isA)
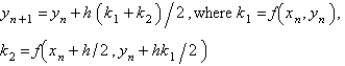
B)
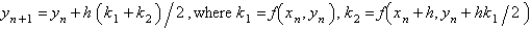
C)
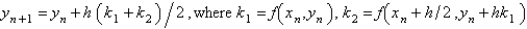
D)
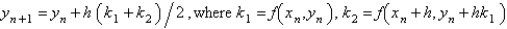
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
The Adams-Bashforth formula for finding the solution of 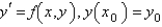 is
is
A)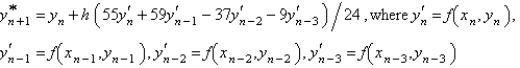
B)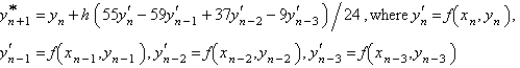
C)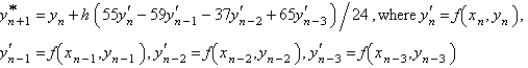
D)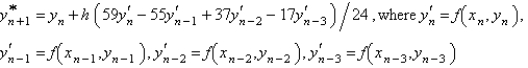
E) none of the above
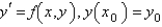 is
isA)
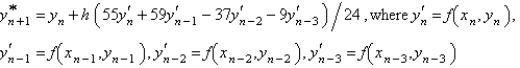
B)
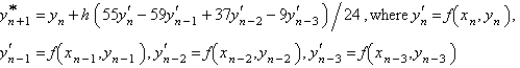
C)
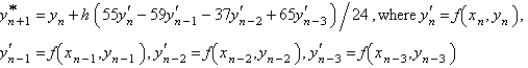
D)
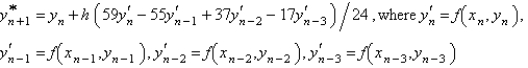
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
Using the method from the previous two problems, using the values 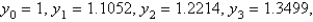 the solution of
the solution of 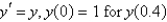 with
with 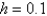 is
is
A) 1.4919
B) 1.4967
C) 1.4978
D) 1.5003
E) none of the above
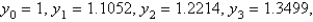 the solution of
the solution of 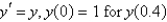 with
with 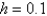 is
isA) 1.4919
B) 1.4967
C) 1.4978
D) 1.5003
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
The solution of 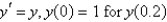 , using the improved Euler's method with
, using the improved Euler's method with 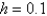 is
is
A) 1.22125
B) 1.210625
C) 1.226525
D) 1.21525
E) 1.221025
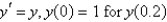 , using the improved Euler's method with
, using the improved Euler's method with 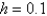 is
isA) 1.22125
B) 1.210625
C) 1.226525
D) 1.21525
E) 1.221025

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
When entering the number 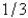 into a three digit base ten calculator, the actual value entered is
into a three digit base ten calculator, the actual value entered is
A)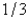
B)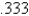
C)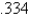
D)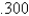
E)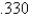
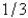 into a three digit base ten calculator, the actual value entered is
into a three digit base ten calculator, the actual value entered isA)
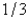
B)
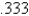
C)
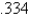
D)
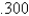
E)
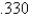

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
The fourth order Runge-Kutta method for solving 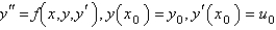 is
is
A)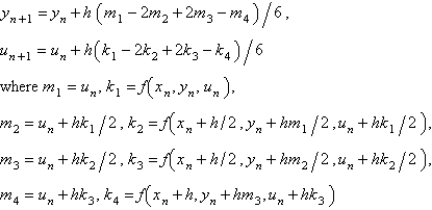
B)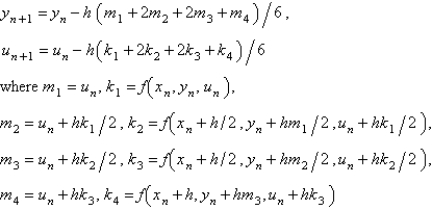
C)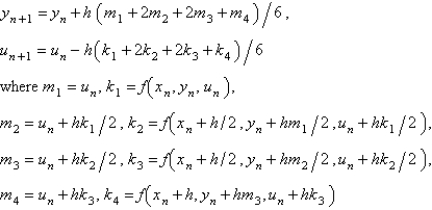
D)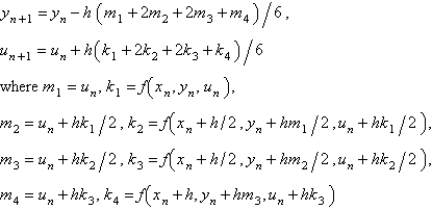
E)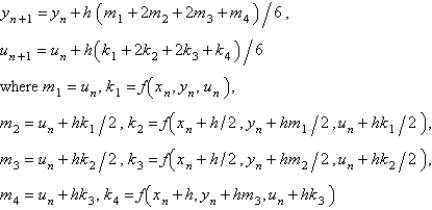
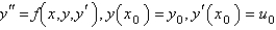 is
isA)
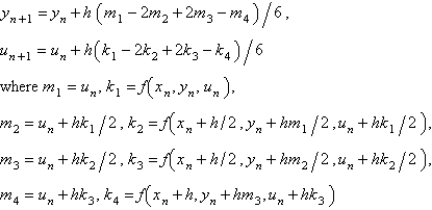
B)
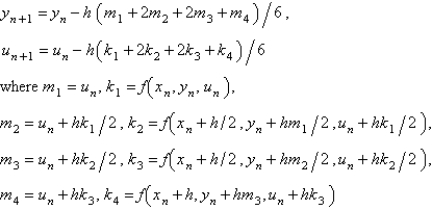
C)
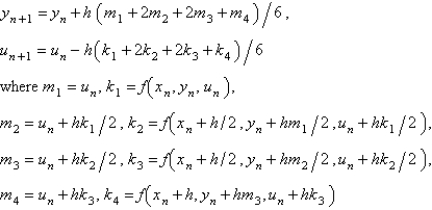
D)
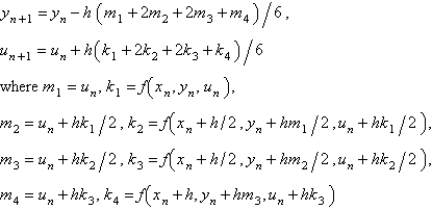
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
The problem 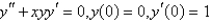 can be written as a system of two equations as follows.
can be written as a system of two equations as follows.
A)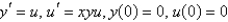
B)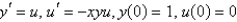
C)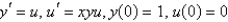
D)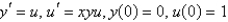
E)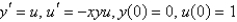
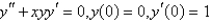 can be written as a system of two equations as follows.
can be written as a system of two equations as follows.A)
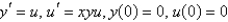
B)
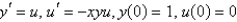
C)
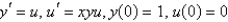
D)
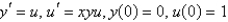
E)
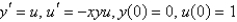

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
Using the value of 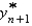 from the previous problem, the Adams-Moulton corrector value for the solution of
from the previous problem, the Adams-Moulton corrector value for the solution of 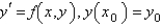 is
is
A)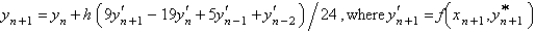
B)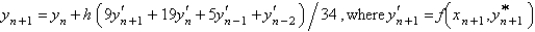
C)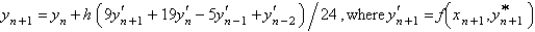
D)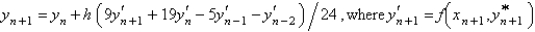
E) none of the above
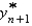 from the previous problem, the Adams-Moulton corrector value for the solution of
from the previous problem, the Adams-Moulton corrector value for the solution of 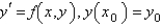 is
isA)
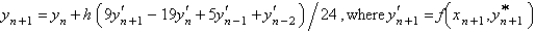
B)
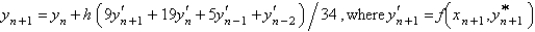
C)
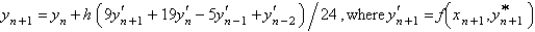
D)
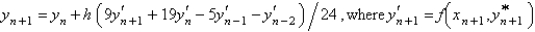
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
In the previous problem, the local truncation error in 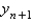 is
is
A)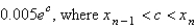
B)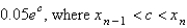
C)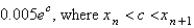
D)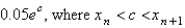
E) unknown
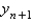 is
isA)
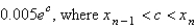
B)
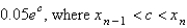
C)
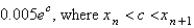
D)
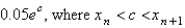
E) unknown

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
Euler's formula for solving 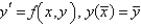 is
is
A)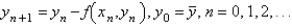
B)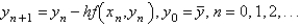
C)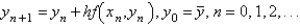
D)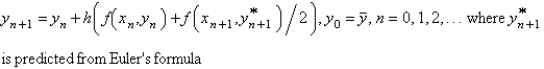
E)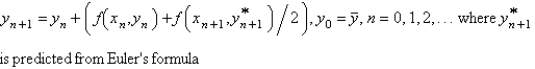
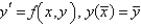 is
isA)
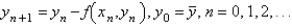
B)
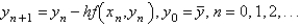
C)
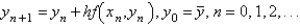
D)
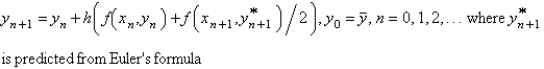
E)
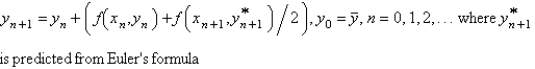

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
When entering the number 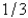 into a three digit base ten calculator, the round-off error is
into a three digit base ten calculator, the round-off error is
A)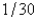
B)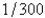
C)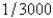
D)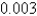
E)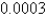
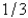 into a three digit base ten calculator, the round-off error is
into a three digit base ten calculator, the round-off error isA)
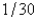
B)
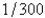
C)
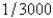
D)
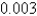
E)
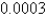

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
Euler's method is what type of Runge-Kutta method?
A) first order
B) second order
C) third order
D) fourth order
E) It is not a Runge-Kutta method
A) first order
B) second order
C) third order
D) fourth order
E) It is not a Runge-Kutta method

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
The most popular fourth order Runge-Kutta method for the solution of 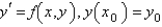 is
is
A)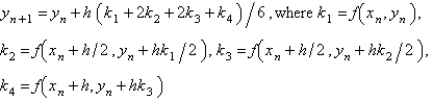
B)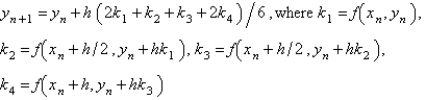
C)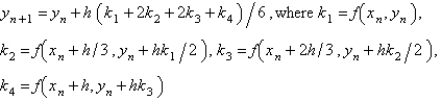
D)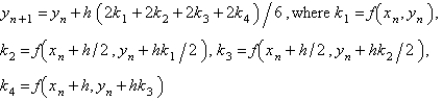
E)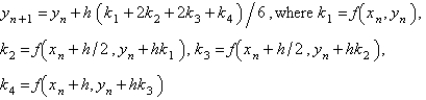
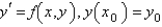 is
isA)
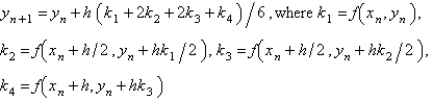
B)
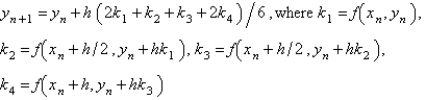
C)
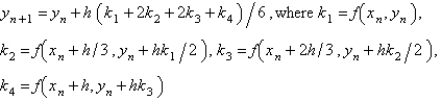
D)
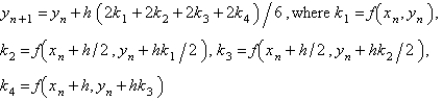
E)
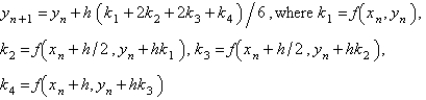

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
The solution of 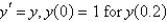 , using Euler's method with
, using Euler's method with 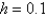 is
is
A) 1.01
B) 1.1
C) 1.11
D) 1.21
E) 1.22
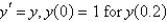 , using Euler's method with
, using Euler's method with 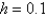 is
isA) 1.01
B) 1.1
C) 1.11
D) 1.21
E) 1.22

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
Using the method from the previous problem, the solution of 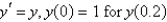 with
with 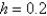 is
is
A) 1.2
B) 1.21
C) 1.214
D) 1.22
E) 1.24
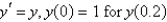 with
with 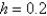 is
isA) 1.2
B) 1.21
C) 1.214
D) 1.22
E) 1.24

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
Using Euler's method on the previous problem and using a value of 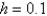 , the solution for
, the solution for 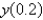 is
is
A) 0.11
B) 0.2
C) 0.21
D) 0.22
E) 0.221
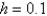 , the solution for
, the solution for 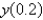 is
isA) 0.11
B) 0.2
C) 0.21
D) 0.22
E) 0.221

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
The local truncation error for the improved Euler's method is
A) unknown
B)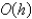
C)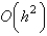
D)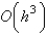
E)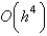
A) unknown
B)
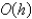
C)
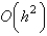
D)
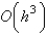
E)
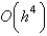

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


