Deck 9: Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/67
Play
Full screen (f)
Deck 9: Differential Equations
1
Solve the initial-value problem. 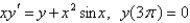
A)
B)
C)
D)
E)
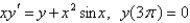
A)

B)

C)

D)

E)


2
Solve the differential equation. 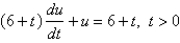
A)
B)
C)
D)
E)
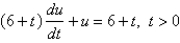
A)

B)

C)

D)

E)


3
Solve the initial-value problem. 
A)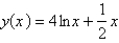
B)
C)
D)
E)

A)
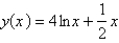
B)

C)

D)

E)


4
Determine whether the differential equation is linear. 
A)the equation is not linear
B)the equation is linear

A)the equation is not linear
B)the equation is linear

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the differential equation. 
A)
B)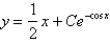
C)
D)
E)

A)

B)
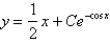
C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
6
In the circuit shown in Figure, a generator supplies a voltage of  volts, the inductance is 2 H, the resistance is 40
volts, the inductance is 2 H, the resistance is 40  , and
, and  . Find the current 0.2 s after the switch is closed. Round your answer to two decimal places.
. Find the current 0.2 s after the switch is closed. Round your answer to two decimal places. 
A) 0.75 A
B)
C)
D)
E)
 volts, the inductance is 2 H, the resistance is 40
volts, the inductance is 2 H, the resistance is 40  , and
, and  . Find the current 0.2 s after the switch is closed. Round your answer to two decimal places.
. Find the current 0.2 s after the switch is closed. Round your answer to two decimal places. 
A) 0.75 A
B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
7
An object with mass m is dropped from rest and we assume that the air resistance is proportional to the speed of the object. If  is the distance dropped after t seconds, then the speed is
is the distance dropped after t seconds, then the speed is  and the acceleration is
and the acceleration is  . If g is the acceleration due to gravity, then the downward force on the object is
. If g is the acceleration due to gravity, then the downward force on the object is 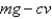 , where c is a positive constant, and Newton's Second Law gives
, where c is a positive constant, and Newton's Second Law gives  .
.
Find the limiting velocity.
 is the distance dropped after t seconds, then the speed is
is the distance dropped after t seconds, then the speed is  and the acceleration is
and the acceleration is  . If g is the acceleration due to gravity, then the downward force on the object is
. If g is the acceleration due to gravity, then the downward force on the object is 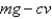 , where c is a positive constant, and Newton's Second Law gives
, where c is a positive constant, and Newton's Second Law gives  .
.Find the limiting velocity.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the initial-value problem. 
A)
B)
C)
D)
E)

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
9
We modeled populations of aphids and ladybugs with a Lotka-Volterra system. Suppose we modify those equations as follows:  ,
, 
A)
B)
C)
D)
E)
 ,
, 
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
10
A phase trajectory is shown for populations of rabbits 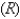 and foxes
and foxes 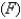 . Describe how each population changes as time goes by.
. Describe how each population changes as time goes by. 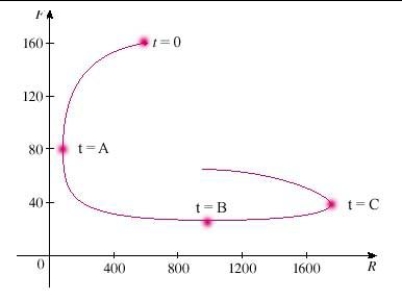 Select the correct statement.
Select the correct statement.
A)At the population of foxes reaches a minimum of about 30.
the population of foxes reaches a minimum of about 30.
B)At the number of rabbits rebounds to 500.
the number of rabbits rebounds to 500.
C)At the number of foxes reaches a maximum of about 2400.
the number of foxes reaches a maximum of about 2400.
 and foxes
and foxes  . Describe how each population changes as time goes by.
. Describe how each population changes as time goes by.  Select the correct statement.
Select the correct statement.A)At
 the population of foxes reaches a minimum of about 30.
the population of foxes reaches a minimum of about 30.B)At
 the number of rabbits rebounds to 500.
the number of rabbits rebounds to 500.C)At
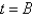 the number of foxes reaches a maximum of about 2400.
the number of foxes reaches a maximum of about 2400.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following functions is a solution of the differential equation? 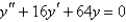
A)
B)
C)
D)
E)
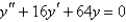
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the differential equation. 
A)
B)
C)
D)
E)

A)

B)

C)

D)

E)

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the differential equation. 


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
14
Determine whether the differential equation is linear. 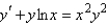
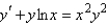

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the initial-value problem. 
A)
B)
C)
D)
E)

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the initial-value problem. 


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the initial-value problem. 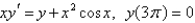
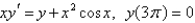

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
18
Find the solution of the initial-value problem and use it to find the population when 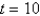 .
. 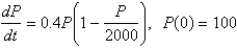
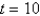 .
. 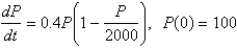

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
19
Let  be the performance level of someone learning a skill as a function of the training time t. The graph of P is called a learning curve. We propose the differential equation
be the performance level of someone learning a skill as a function of the training time t. The graph of P is called a learning curve. We propose the differential equation  as a reasonable model for learning, where r is a positive constant. Solve it as a linear differential equation.
as a reasonable model for learning, where r is a positive constant. Solve it as a linear differential equation.
A)
B)
C)
D)
E)
 be the performance level of someone learning a skill as a function of the training time t. The graph of P is called a learning curve. We propose the differential equation
be the performance level of someone learning a skill as a function of the training time t. The graph of P is called a learning curve. We propose the differential equation  as a reasonable model for learning, where r is a positive constant. Solve it as a linear differential equation.
as a reasonable model for learning, where r is a positive constant. Solve it as a linear differential equation.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the initial-value problem. 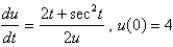
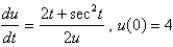

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose that a population grows according to a logistic model with carrying capacity  and
and  per year. Choose the logistic differential equation for these data.
per year. Choose the logistic differential equation for these data.
A)
B)
C)
D)
E)
 and
and  per year. Choose the logistic differential equation for these data.
per year. Choose the logistic differential equation for these data.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
22
Let  .
.
What are the equilibrium solutions?
 .
.What are the equilibrium solutions?

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
23
The population of the world was about 5.3 billion in 1990. Birth rates in the 1990s range from 35 to 40 million per year and death rates range from 15 to 20 million per year. Let's assume that the carrying capacity for world population is 100 billion. Use the logistic model to predict the world population in the 2,450 year. Calculate your answer in billions to one decimal place. (Because the initial population is small compared to the carrying capacity, you can take k to be an estimate of the initial relative growth rate.)
A)59.2 billion
B)32.9 billion
C)78.3 billion
D)17.1 billion
E)24.1 billion
A)59.2 billion
B)32.9 billion
C)78.3 billion
D)17.1 billion
E)24.1 billion

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
24
The rate of change of atmospheric pressure P with respect to altitude h is proportional to P provided that the temperature is constant. At 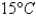 the pressure is
the pressure is 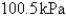 at sea level and
at sea level and 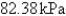 at
at 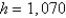 . What is the pressure at an altitude of
. What is the pressure at an altitude of 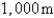 ?
?
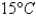 the pressure is
the pressure is 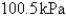 at sea level and
at sea level and 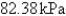 at
at 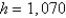 . What is the pressure at an altitude of
. What is the pressure at an altitude of 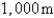 ?
?
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
25
Let c be a positive number. A differential equation of the form  where k is a positive constant, is called a doomsday equation because the exponent in the expression
where k is a positive constant, is called a doomsday equation because the exponent in the expression  is larger than the exponent 1for natural growth. An especially prolific breed of rabbits has the growth term
is larger than the exponent 1for natural growth. An especially prolific breed of rabbits has the growth term  . If
. If  such rabbits breed initially and the warren has
such rabbits breed initially and the warren has  rabbits after
rabbits after  months, then when is doomsday?
months, then when is doomsday?
 where k is a positive constant, is called a doomsday equation because the exponent in the expression
where k is a positive constant, is called a doomsday equation because the exponent in the expression  is larger than the exponent 1for natural growth. An especially prolific breed of rabbits has the growth term
is larger than the exponent 1for natural growth. An especially prolific breed of rabbits has the growth term  . If
. If  such rabbits breed initially and the warren has
such rabbits breed initially and the warren has  rabbits after
rabbits after  months, then when is doomsday?
months, then when is doomsday?
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the differential equation  as a model for a fish population, where t is measured in weeks and c is a constant. For what values of c does the fish population always die out?
as a model for a fish population, where t is measured in weeks and c is a constant. For what values of c does the fish population always die out?
 as a model for a fish population, where t is measured in weeks and c is a constant. For what values of c does the fish population always die out?
as a model for a fish population, where t is measured in weeks and c is a constant. For what values of c does the fish population always die out?
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
27
One model for the spread of a rumor is that the rate of spread is proportional to the product of the fraction of the population who have heard the rumor and the fraction who have not heard the rumor. Let's assume that the constant of proportionality is  . Write a differential equation that is satisfied by y.
. Write a differential equation that is satisfied by y.
 . Write a differential equation that is satisfied by y.
. Write a differential equation that is satisfied by y.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
28
The Pacific halibut fishery has been modeled by the differential equation  where
where  is the biomass (the total mass of the members of the population) in kilograms at time t (measured in years), the carrying capacity is estimated to be
is the biomass (the total mass of the members of the population) in kilograms at time t (measured in years), the carrying capacity is estimated to be  and
and  per year. If
per year. If  , find the biomass a year later.
, find the biomass a year later.
 where
where  is the biomass (the total mass of the members of the population) in kilograms at time t (measured in years), the carrying capacity is estimated to be
is the biomass (the total mass of the members of the population) in kilograms at time t (measured in years), the carrying capacity is estimated to be  and
and  per year. If
per year. If  , find the biomass a year later.
, find the biomass a year later.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose that a population grows according to a logistic model with carrying capacity 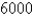 and
and 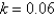 per year. Write the logistic differential equation for these data.
per year. Write the logistic differential equation for these data.
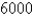 and
and 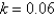 per year. Write the logistic differential equation for these data.
per year. Write the logistic differential equation for these data.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
30
Let c be a positive number. A differential equation of the form  where k is a positive constant is called a doomsday equation because the exponent in the expression
where k is a positive constant is called a doomsday equation because the exponent in the expression  is larger than the exponent 1 for natural growth. An especially prolific breed of rabbits has the growth term
is larger than the exponent 1 for natural growth. An especially prolific breed of rabbits has the growth term  . If
. If  such rabbits breed initially and the warren has
such rabbits breed initially and the warren has  rabbits after
rabbits after  months, then when is doomsday?
months, then when is doomsday?
A)
B)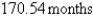
C)
D)
E)
 where k is a positive constant is called a doomsday equation because the exponent in the expression
where k is a positive constant is called a doomsday equation because the exponent in the expression  is larger than the exponent 1 for natural growth. An especially prolific breed of rabbits has the growth term
is larger than the exponent 1 for natural growth. An especially prolific breed of rabbits has the growth term  . If
. If  such rabbits breed initially and the warren has
such rabbits breed initially and the warren has  rabbits after
rabbits after  months, then when is doomsday?
months, then when is doomsday?A)

B)
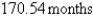
C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
31
A curve passes through the point 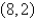 and has the property that the slope of the curve at every point P is
and has the property that the slope of the curve at every point P is 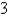 times the y-coordinate P. What is the equation of the curve?
times the y-coordinate P. What is the equation of the curve?
A)
B)
C)
D)
E)
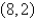 and has the property that the slope of the curve at every point P is
and has the property that the slope of the curve at every point P is 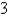 times the y-coordinate P. What is the equation of the curve?
times the y-coordinate P. What is the equation of the curve?A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
32
Biologists stocked a lake with  fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be
fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be  . The number of fish tripled in the first year. Assuming that the size of the fish population satisfies the logistic equation, find an expression for the size of the population after t years.
. The number of fish tripled in the first year. Assuming that the size of the fish population satisfies the logistic equation, find an expression for the size of the population after t years.
 fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be
fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be  . The number of fish tripled in the first year. Assuming that the size of the fish population satisfies the logistic equation, find an expression for the size of the population after t years.
. The number of fish tripled in the first year. Assuming that the size of the fish population satisfies the logistic equation, find an expression for the size of the population after t years.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the differential equation. 
A)
B)
C)
D)
E)

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
34
The population of the world was about 5.3 billion in 1990. Birth rates in the 1990s range from 35 to 40 million per year and death rates range from 15 to 20 million per year. Let's assume that the carrying capacity for world population is 100 billion. Use the logistic model to predict the world population in the 2,450 year. Calculate your answer in billions to one decimal place. (Because the initial population is small compared to the carrying capacity, you can take k to be an estimate of the initial relative growth rate.)
A)24.1 billion
B)32.9 billion
C)59.2 billion
D)78.3 billion
E)17.1 billion
A)24.1 billion
B)32.9 billion
C)59.2 billion
D)78.3 billion
E)17.1 billion

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
35
One model for the spread of an epidemic is that the rate of spread is jointly proportional to the number of infected people and the number of uninfected people. In an isolated town of  inhabitants,
inhabitants,  people have a disease at the beginning of the week and
people have a disease at the beginning of the week and  have it at the end of the week. How long does it take for
have it at the end of the week. How long does it take for  of the population to be infected?
of the population to be infected?
A)
B)
C)
D)
E)
 inhabitants,
inhabitants,  people have a disease at the beginning of the week and
people have a disease at the beginning of the week and  have it at the end of the week. How long does it take for
have it at the end of the week. How long does it take for  of the population to be infected?
of the population to be infected?A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
36
A sum of 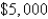 is invested at
is invested at 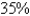 interest. If
interest. If 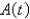 is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by
is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by 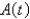 .
.
A)
B)
C)
D)
E)
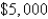 is invested at
is invested at 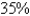 interest. If
interest. If 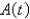 is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by
is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by 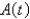 .
.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
37
Suppose that a population develops according to the logistic equation 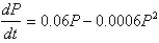 , where t is measured in weeks. What is the carrying capacity?
, where t is measured in weeks. What is the carrying capacity?
A)
B)
C)
D)
E)
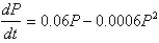 , where t is measured in weeks. What is the carrying capacity?
, where t is measured in weeks. What is the carrying capacity?A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
38
One model for the spread of an epidemic is that the rate of spread is jointly proportional to the number of infected people and the number of uninfected people. In an isolated town of  inhabitants,
inhabitants,  people have a disease at the beginning of the week and
people have a disease at the beginning of the week and  have it at the end of the week. How long does it take for
have it at the end of the week. How long does it take for  of the population to be infected?
of the population to be infected?
 inhabitants,
inhabitants,  people have a disease at the beginning of the week and
people have a disease at the beginning of the week and  have it at the end of the week. How long does it take for
have it at the end of the week. How long does it take for  of the population to be infected?
of the population to be infected?
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
39
A common inhabitant of human intestines is the bacterium Escherichia coli. A cell of this bacterium in a nutrient-broth medium divides into two cells every 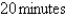 . The initial population of a culture is
. The initial population of a culture is 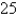 cells. Find the number of cells after
cells. Find the number of cells after 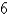 hours.
hours.
A)
B)
C)
D)
E)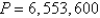
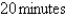 . The initial population of a culture is
. The initial population of a culture is 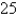 cells. Find the number of cells after
cells. Find the number of cells after 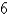 hours.
hours.A)

B)

C)

D)

E)
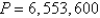

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the differential equation. 
A)
B)
C)
D)
E)

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
41
Experiments show that if the chemical reaction 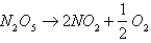 takes place at
takes place at 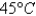 , the rate of reaction of dinitrogen pentoxide is proportional to its concentration as follows :
, the rate of reaction of dinitrogen pentoxide is proportional to its concentration as follows : 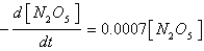 How long will the reaction take to reduce the concentration of
How long will the reaction take to reduce the concentration of 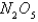 to 50% of its original value?
to 50% of its original value?
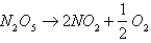 takes place at
takes place at 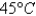 , the rate of reaction of dinitrogen pentoxide is proportional to its concentration as follows :
, the rate of reaction of dinitrogen pentoxide is proportional to its concentration as follows : 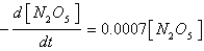 How long will the reaction take to reduce the concentration of
How long will the reaction take to reduce the concentration of 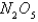 to 50% of its original value?
to 50% of its original value?
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the differential equation. 


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
43
A certain small country has $20 billion in paper currency in circulation, and each day $70 million comes into the country's banks. The government decides to introduce new currency by having the banks replace old bills with new ones whenever old currency comes into the banks. Let  denote the amount of new currency in circulation at time t with
denote the amount of new currency in circulation at time t with  . Formulate and solve a mathematical model in the form of an initial-value problem that represents the "flow" of the new currency into circulation (in billions per day).
. Formulate and solve a mathematical model in the form of an initial-value problem that represents the "flow" of the new currency into circulation (in billions per day).
 denote the amount of new currency in circulation at time t with
denote the amount of new currency in circulation at time t with  . Formulate and solve a mathematical model in the form of an initial-value problem that represents the "flow" of the new currency into circulation (in billions per day).
. Formulate and solve a mathematical model in the form of an initial-value problem that represents the "flow" of the new currency into circulation (in billions per day).
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the differential equation. 


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
45
Find the solution of the differential equation that satisfies the initial condition  .
. 
 .
. 

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
46
Find the orthogonal trajectories of the family of curves. 
A)
B)
C)
D)
E)

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
47
Select a direction field for the differential equation  from a set of direction fields labeled I-IV.
from a set of direction fields labeled I-IV. 
 from a set of direction fields labeled I-IV.
from a set of direction fields labeled I-IV. 

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
48
A population is modeled by the differential equation.  For what values of P is the population increasing?
For what values of P is the population increasing?
A)
B)
C)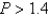
D)
E)
 For what values of P is the population increasing?
For what values of P is the population increasing?A)

B)

C)
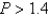
D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
49
Choose the differential equation corresponding to this direction field. 
A)
B)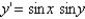
C)
D)
E)

A)

B)
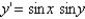
C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
50
Find the orthogonal trajectories of the family of curves. 


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the differential equation. 


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
52
A tank contains  L of brine with
L of brine with  kg of dissolved salt. Pure water enters the tank at a rate of
kg of dissolved salt. Pure water enters the tank at a rate of  L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank after
L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank after  minutes?
minutes?
 L of brine with
L of brine with  kg of dissolved salt. Pure water enters the tank at a rate of
kg of dissolved salt. Pure water enters the tank at a rate of  L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank after
L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank after  minutes?
minutes?
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
53
Which equation does the function 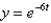 satisfy?
satisfy?
A)
B)
C)
D)
E)
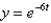 satisfy?
satisfy?A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the initial-value problem. 
A)
B)
C)
D)
E)

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
55
Find the solution of the differential equation 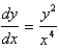 that satisfies the initial condition
that satisfies the initial condition 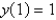 .
.
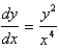 that satisfies the initial condition
that satisfies the initial condition 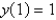 .
.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
56
Use Euler's method with step size 0.1 to estimate  , where
, where  is the solution of the initial-value problem. Round your answer to four decimal places.
is the solution of the initial-value problem. Round your answer to four decimal places. 
 , where
, where  is the solution of the initial-value problem. Round your answer to four decimal places.
is the solution of the initial-value problem. Round your answer to four decimal places. 

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
57
Use Euler's method with step size 0.25 to estimate 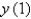 , where
, where 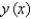 is the solution of the initial-value problem. Round your answer to four decimal places.
is the solution of the initial-value problem. Round your answer to four decimal places. 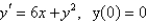
A)
B)
C)
D)
E)
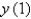 , where
, where 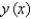 is the solution of the initial-value problem. Round your answer to four decimal places.
is the solution of the initial-value problem. Round your answer to four decimal places. 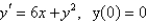
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the differential equation. 
A)
B)
C)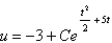
D)
E)

A)

B)

C)
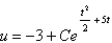
D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
59
The solution of the differential equation  satisfies the initial condition
satisfies the initial condition  .
.
Find the limit.
 satisfies the initial condition
satisfies the initial condition  .
.Find the limit.


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
60
Kirchhoff's Law gives us the derivative equation  .
.
If , use Euler's method with step size 0.1 to estimate
, use Euler's method with step size 0.1 to estimate  after 0.3 second.
after 0.3 second.
 .
.If
 , use Euler's method with step size 0.1 to estimate
, use Euler's method with step size 0.1 to estimate  after 0.3 second.
after 0.3 second.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
61
For what nonzero values of k does the function 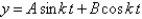 satisfy the differential equation
satisfy the differential equation 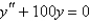 for all values of A and B?
for all values of A and B?
A)
B)
C)
D)
E)
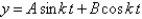 satisfy the differential equation
satisfy the differential equation 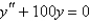 for all values of A and B?
for all values of A and B? A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
62
For what values of k does the function  satisfy the differential equation
satisfy the differential equation  ?
?
A)
B)
C)
D)
E)
 satisfy the differential equation
satisfy the differential equation  ?
? A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
63
Newton's Law of Cooling states that the rate of cooling of an object is proportional to the temperature difference between the object and its surroundings. Suppose that a roast turkey is taken from an oven when its temperature has reached  and is placed on a table in a room where the temperature is
and is placed on a table in a room where the temperature is  . If
. If  is the temperature of the turkey after t minutes, then Newton's Law of Cooling implies that
is the temperature of the turkey after t minutes, then Newton's Law of Cooling implies that 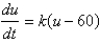 . This could be solved as a separable differential equation. Another method is to make the change of variable
. This could be solved as a separable differential equation. Another method is to make the change of variable  . If the temperature of the turkey is
. If the temperature of the turkey is  after half an hour, what is the temperature after 35 min?
after half an hour, what is the temperature after 35 min?
A)
B)
C)
D)
E)
 and is placed on a table in a room where the temperature is
and is placed on a table in a room where the temperature is  . If
. If  is the temperature of the turkey after t minutes, then Newton's Law of Cooling implies that
is the temperature of the turkey after t minutes, then Newton's Law of Cooling implies that 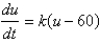 . This could be solved as a separable differential equation. Another method is to make the change of variable
. This could be solved as a separable differential equation. Another method is to make the change of variable  . If the temperature of the turkey is
. If the temperature of the turkey is  after half an hour, what is the temperature after 35 min?
after half an hour, what is the temperature after 35 min?A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
64
A population is modeled by the differential equation 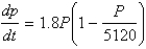 .
.
For what values of P is the population decreasing?
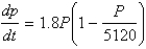 .
.For what values of P is the population decreasing?

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
65
Which of the following functions are the constant solutions of the equation 
a.
b.
c.
d.
e.

a.

b.

c.

d.

e.


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
66
A sum of  is invested at
is invested at  interest. If
interest. If  is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by
is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by  .
.
 is invested at
is invested at  interest. If
interest. If  is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by
is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by  .
.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
67
A function 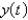 satisfies the differential equation
satisfies the differential equation 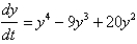 .
.
What are the constant solutions of the equation?
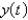 satisfies the differential equation
satisfies the differential equation 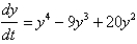 .
.What are the constant solutions of the equation?

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck


