Deck 11: Waiting Line Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/56
Play
Full screen (f)
Deck 11: Waiting Line Models
1
Little's flow equations indicate that the relationship of L to Lq is the same as that of W to Wq.
False
2
Before waiting lines can be analyzed economically,the arrivals' cost of waiting must be estimated.
True
3
Waiting line models describe the transient-period operating characteristics of a waiting line.
False
4
For a single-server queuing system,the average number of customers in the waiting line is one less than the average number in the system.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
5
In waiting line applications,the exponential probability distribution indicates that approximately 63% of the service times are less than the mean service time.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
6
Kendall's notation is helpful when classifying the wide variety of different waiting line models and can indicate that the waiting line system is assumed to have infinite capacity.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
7
After the startup or transient period,a waiting system is in steady-state operation and considered to be the normal operation of the waiting line.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
8
When blocked customers are cleared,an important decision is how many servers to provide.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
9
Use of the Poisson probability distribution assumes that arrivals are not random.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
10
A waiting line situation with a single server is referred to as an M/M/1 model with a finite calling population.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
11
For an M/M/1 queuing system,if the service rate,µ,is doubled,the average wait in the system,W,is cut in half.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
12
A multiple-server waiting line is one that has two or more parallel service facilities.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
13
Queue discipline refers to the assumption that a customer has the patience to remain in a slow moving queue.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
14
Adding more servers always improves the operating characteristics of the waiting line and reduces the waiting cost.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
15
For a single-server waiting line,the utilization factor is the probability that an arriving unit must wait for service.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
16
Queue discipline refers to the manner in which waiting units are arranged for service.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
17
In developing the total cost for a waiting line,waiting cost takes into consideration both the time spent waiting in line and the time spent being served.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
18
In waiting line systems where the length of the waiting line is limited,the mean number of units entering the system might be less than the arrival rate.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
19
A variation of the waiting line models involves a system in which no waiting is allowed,and arriving units are denied access to the system.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
20
If service time follows an exponential probability distribution,approximately 63% of the service times are less than the mean service time.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
21
Single-booth ticket sales at a theater are an example of which of the following queuing models?
A)single-server,Poisson service rate distribution,unlimited queue length
B)single-server,Poisson service rate distribution,limited queue length
C)single-server,constant service rate distribution,unlimited queue length
D)single-server,normal service rate distribution,unlimited queue length
A)single-server,Poisson service rate distribution,unlimited queue length
B)single-server,Poisson service rate distribution,limited queue length
C)single-server,constant service rate distribution,unlimited queue length
D)single-server,normal service rate distribution,unlimited queue length

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
22
Little's flow equations can apply to a single-server as well as multiple-server waiting line model.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
23
The body of knowledge dealing with waiting lines is known as queueing theory.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
24
The equations provided in the textbook for computing operating characteristics apply to a waiting line operating
A)at start-up.
B)at steady state.
C)at peak demand times.
D)in transition.
A)at start-up.
B)at steady state.
C)at peak demand times.
D)in transition.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
25
If arrivals occur according to the Poisson distribution every 20 minutes,then which of the following is NOT true?
A)λ = 20 arrivals per hour
B)λ = 3 arrivals per hour
C)λ = 1/20 arrivals per minute
D)λ = 72 arrivals per day
A)λ = 20 arrivals per hour
B)λ = 3 arrivals per hour
C)λ = 1/20 arrivals per minute
D)λ = 72 arrivals per day

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
26
The mean number of units that can be served per time period is called
A)the service rate and is denoted by λ.
B)the service rate and is denoted by μ.
C)the steady state.
D)None of these are correct.
A)the service rate and is denoted by λ.
B)the service rate and is denoted by μ.
C)the steady state.
D)None of these are correct.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
27
The assumption of exponentially distributed service times indicates that
A)37% of the service times are less than the mean service time.
B)50% of the service times are less than the mean service time.
C)63% of the service times are less than the mean service time.
D)service time increase at an exponential rate as the waiting line grows.
A)37% of the service times are less than the mean service time.
B)50% of the service times are less than the mean service time.
C)63% of the service times are less than the mean service time.
D)service time increase at an exponential rate as the waiting line grows.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
28
The arrival rate in queuing formulas is expressed as the
A)mean time between arrivals.
B)minimum number of arrivals per time period.
C)mean number of arrivals per server.
D)mean number of arrivals per time period.
A)mean time between arrivals.
B)minimum number of arrivals per time period.
C)mean number of arrivals per server.
D)mean number of arrivals per time period.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
29
Decision makers in queuing situations attempt to balance
A)operating characteristics against the arrival rate.
B)service levels against service cost.
C)the number of units in the system against the time in the system.
D)the service rate against the arrival rate.
A)operating characteristics against the arrival rate.
B)service levels against service cost.
C)the number of units in the system against the time in the system.
D)the service rate against the arrival rate.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
30
Little's flow equations
A)require Poisson and exponential assumptions.
B)are applicable to any waiting line model.
C)require independent calculation of W,L,Wq,and Lq.
D)All of these are correct.
A)require Poisson and exponential assumptions.
B)are applicable to any waiting line model.
C)require independent calculation of W,L,Wq,and Lq.
D)All of these are correct.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
31
Models with a finite calling population
A)have an arrival rate independent of the number of units in the system.
B)have a service rate dependent on the number of units in the system.
C)have no limit placed on how many units may seek service.
D)All of these are correct.
A)have an arrival rate independent of the number of units in the system.
B)have a service rate dependent on the number of units in the system.
C)have no limit placed on how many units may seek service.
D)All of these are correct.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
32
The manner in which units receive their service,such as FCFS,is the
A)queue discipline.
B)server.
C)steady state.
D)operating characteristic.
A)queue discipline.
B)server.
C)steady state.
D)operating characteristic.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
33
The total cost for a waiting line does NOT specifically depend on the
A)cost of waiting.
B)cost of service.
C)number of units in the system.
D)cost of a lost customer.
A)cost of waiting.
B)cost of service.
C)number of units in the system.
D)cost of a lost customer.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
34
Performance measures dealing with the number of units in line and the time spent waiting are called
A)queuing facts.
B)performance queues.
C)system measures.
D)operating characteristics.
A)queuing facts.
B)performance queues.
C)system measures.
D)operating characteristics.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
35
In a waiting line situation,arrivals occur,on average,every 10 minutes,and 10 units can be received every hour.Which of the following represents λ and μ in this situation?
A)λ = 10,μ = 10
B)λ = 6,μ = 6
C)λ = 6,μ = 10
D)λ = 10,μ = 6
A)λ = 10,μ = 10
B)λ = 6,μ = 6
C)λ = 6,μ = 10
D)λ = 10,μ = 6

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
36
Operating characteristics formulas for the single-server queue do NOT require
A)λ ≥ μ.
B)Poisson distribution of arrivals.
C)an exponential distribution of service times.
D)an FCFS queue discipline.
A)λ ≥ μ.
B)Poisson distribution of arrivals.
C)an exponential distribution of service times.
D)an FCFS queue discipline.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
37
Waiting line models consist of mathematical formulas and relationships that can be used to determine the operating characteristics (also known as performance measures)for a waiting line.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
38
When no limit is placed on how many units may seek service,the waiting line model
A)can assume that no units are in the system.
B)is said to have an infinite calling population.
C)maintains a constant arrival rate.
D)None of these are correct.
A)can assume that no units are in the system.
B)is said to have an infinite calling population.
C)maintains a constant arrival rate.
D)None of these are correct.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
39
For many waiting line situations,the arrivals occur randomly and independently of other arrivals and it has been found that a good description of the arrival pattern is provided by a(n)
A)normal probability distribution.
B)exponential probability distribution.
C)uniform probability distribution.
D)Poisson probability distribution.
A)normal probability distribution.
B)exponential probability distribution.
C)uniform probability distribution.
D)Poisson probability distribution.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following queue disciplines is assumed by the waiting line models presented in the textbook?
A)first-come,first-served
B)last-in,first-out
C)shortest processing,time first
D)first-in,last-out
A)first-come,first-served
B)last-in,first-out
C)shortest processing,time first
D)first-in,last-out

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
41
Arrivals at a box office in the hour before the show follow the Poisson distribution with λ = 7 per minute.Service times are constant at 7.5 seconds.Find the average length of the waiting line.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
42
For an M/G/1 system with λ = 20,μ = 35,and σ = 0.005,find
a.the probability the system is idle.
b.the average length of the queue.
c.the average number in the system.
a.the probability the system is idle.
b.the average length of the queue.
c.the average number in the system.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
43
During summer weekdays,boats arrive at the inlet drawbridge according to the Poisson distribution at a rate of three per hour.In a two-hour period,
a.what is the probability that no boats arrive?
b.what is the probability that two boats arrive?
c.what is the probability that eight boats arrive?
a.what is the probability that no boats arrive?
b.what is the probability that two boats arrive?
c.what is the probability that eight boats arrive?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
44
Circle Electric Supply is considering opening a second service counter to better serve the electrical contractor customers.The arrival rate is 10 per hour.The service rate is 14 per hour.If the cost of waiting is $30 and the cost of each service counter is $22 per hour,should the second counter be opened?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
45
Two new checkout scanning systems are under consideration by a retail store.Arrivals to the checkout stand follow the Poisson distribution with λ = 2 per minute.The cost for waiting is $18 per hour.The first system has an exponential service rate of five per minute and costs $10 per hour to operate.The second system has an exponential service rate of eight per minute and costs $20 per hour to operate.Which system should be chosen?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
46
Quick Clean Rooter cleans out clogged drains.Due to the competitive nature of the drain cleaning business,if a customer calls Quick Clean and finds the line busy,they immediately try another company and Quick Clean loses the business.Quick Clean management estimates that,on average,a customer tries to call Quick Clean every three minutes and the average time to take a service order is 200 seconds.The company wishes to hire enough operators so that at most 4% of its potential customers get the busy signal.
a.How many operators should be hired to meet this objective?
b.Given your answer to part (a),what is the probability that all the operators are idle?
a.How many operators should be hired to meet this objective?
b.Given your answer to part (a),what is the probability that all the operators are idle?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
47
The time to process a registration at the Sea View Resort follows the exponential distribution and has a mean of six minutes.
a.What is the probability of a registration time shorter than three minutes?
b.What is the probability of a registration time shorter than six minutes?
c.What is the probability of a registration time between three and six minutes?
a.What is the probability of a registration time shorter than three minutes?
b.What is the probability of a registration time shorter than six minutes?
c.What is the probability of a registration time between three and six minutes?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
48
The eight students in a seminar class must come to the professor's office to turn in a paper and give a five-minute oral summary.Assume there is a service rate of 10 per hour and adequate time is available for all.The arrival rate for each unit is five per hour.What is the probability there is no one in the office or waiting when you come?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
49
The insurance department at Shear's has two agents,each working at a mean speed of eight customers per hour.Customers arrive at the insurance desk at a mean rate of one every six minutes and form a single queue.Management feels that some customers are going to find the wait at the desk too long and take their business to Word's,Shear's competitor.
In order to reduce the time required by an agent to serve a customer,Shear's is contemplating installing one of two minicomputer systems: System A that leases for $18 per day and will increase an agent's efficiency by 25% or System B that leases for $23 per day and will increase an agent's efficiency by 50%.Agents work eight-hour days.
If Shear's estimates its cost of having a customer in the system at $3 per hour,determine if it should install a new minicomputer system,and if so,which one?
In order to reduce the time required by an agent to serve a customer,Shear's is contemplating installing one of two minicomputer systems: System A that leases for $18 per day and will increase an agent's efficiency by 25% or System B that leases for $23 per day and will increase an agent's efficiency by 50%.Agents work eight-hour days.
If Shear's estimates its cost of having a customer in the system at $3 per hour,determine if it should install a new minicomputer system,and if so,which one?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
50
The Arctic Flyers minor league hockey team has one box office clerk.On average,each customer that comes to see a game can be sold a ticket at the rate of eight per minute.For normal games,customers arrive at the rate of five per minute.Assume arrivals follow the Poisson distribution and service times follow the exponential distribution.
a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Flyers are playing in the league playoffs and anticipate more fans,estimating that the arrival rate will increase to 12 per minute.Output is supplied for two- and three-cashier systems.
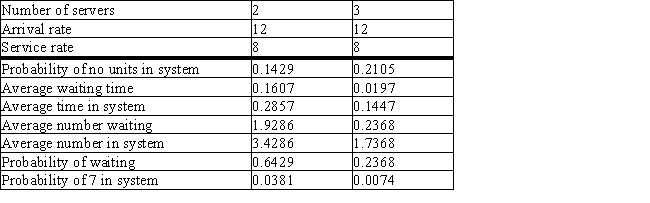

a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Flyers are playing in the league playoffs and anticipate more fans,estimating that the arrival rate will increase to 12 per minute.Output is supplied for two- and three-cashier systems.



Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
51
A company has tool cribs where workmen draw parts.Two men have applied for the position of distributing parts to the workmen.George Fuller is fresh out of trade school and expects a $6 per hour salary.His average service time is four minutes.John Cox is a veteran who expects $12 per hour.His average service time is two minutes.A workman's time is figured at $10 per hour.Workmen arrive to draw parts at an average rate of 12 per hour.
a.What is the average waiting time a workman would spend in the system under each applicant?
b.Which applicant should be hired?
a.What is the average waiting time a workman would spend in the system under each applicant?
b.Which applicant should be hired?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
52
Andy Archer,Ph.D.,is a training consultant for six mid-sized manufacturing firms.On average,each of his six clients calls him for consulting assistance once every 25 days.Andy typically spends an average of five days at the client's firm during each consultation.Assuming the time between client calls follows an exponential distribution,determine
a.the average number of clients Andy has on backlog.
b.the average time a client must wait before Andy arrives.
c.the proportion of time Andy is busy.
a.the average number of clients Andy has on backlog.
b.the average time a client must wait before Andy arrives.
c.the proportion of time Andy is busy.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
53
The Grand Movie Theater has one box office clerk.On average,each customer that comes to see a movie can be sold a ticket at the rate of six per minute.For the theater's normal offerings of older movies,customers arrive at the rate of three per minute.Assume arrivals follow the Poisson distribution and service times follow the exponential distribution.
a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Grand has booked the Stars Wars Trilogy and expects more customers.From conversations with other theater owners,it estimates that the arrival rate will increase to 10 per minute.Output is supplied for two- and three-cashier systems.
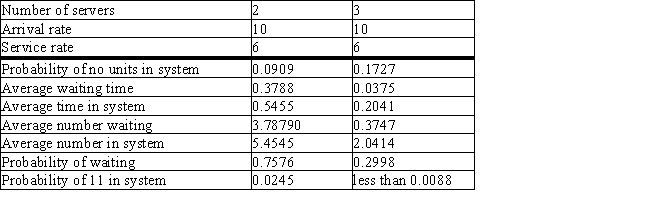
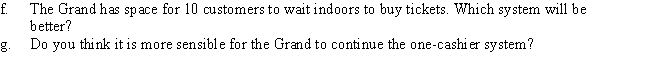
a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Grand has booked the Stars Wars Trilogy and expects more customers.From conversations with other theater owners,it estimates that the arrival rate will increase to 10 per minute.Output is supplied for two- and three-cashier systems.


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
54
For an M/G/1 system with λ = 6,μ = 9,and σ = 0.03,find
a.the probability the system is idle.
b.the average length of the queue.
c.the average number in the system.
a.the probability the system is idle.
b.the average length of the queue.
c.the average number in the system.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
55
The postmaster at the Oak Hill Post Office expects that the mean arrival rate of people to her customer counter will soon increase by 50% due to a large apartment complex being built.Currently,the mean arrival rate is 15 people per hour.The postmaster can serve an average of 25 people per hour.By what percentage must the postmaster's mean service rate increase when the apartment complex is completed in order that the average time spent at the post office remains at its current value?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
56
The Quick Snap photo machine at the Lemon County bus station takes four snapshots in exactly 75 seconds.Customers arrive at the machine according to a Poisson distribution at the mean rate of 20 per hour.On the basis of this information,determine
a.the average number of customers waiting to use the photo machine.
b.the average time a customer spends using the system.
c.the probability an arriving customer must wait for service.
a.the average number of customers waiting to use the photo machine.
b.the average time a customer spends using the system.
c.the probability an arriving customer must wait for service.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck


