Deck 10: Conservation of Angular Momentum
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/67
Play
Full screen (f)
Deck 10: Conservation of Angular Momentum
1
A wheel is set spinning and is then hung by a rope placed at one end of the axle. If the wheel is spinning as shown, the angular momentum of the wheel could be represented by vector 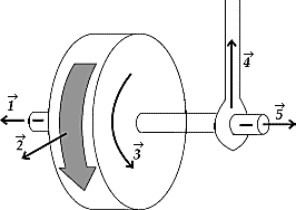
A)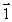
B)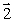
C)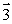
D)
E)

A)
B)
C)
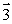
D)
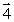
E)
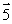
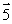
2
We would like to compare the angular momentum of Mars about its axis of rotation with that of Earth's. The mass of Mars is 11% that of Earth, with a radius 53% that of Earth, and a rotational period 103% that of Earth. Assuming both planets to be uniform spheres calculate the ratio of the angular momentum of Mars to that of Earth.
A) 6.0 10-2
B) 5.7 10-2
C) 3.2 10-2
D) 3.0 10-2
E) 3.1 10-2
A) 6.0 10-2
B) 5.7 10-2
C) 3.2 10-2
D) 3.0 10-2
E) 3.1 10-2
3.0 10-2
3
The vector 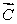 represents
represents 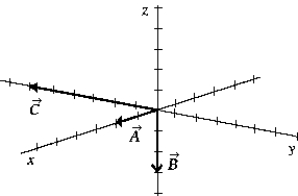
A)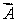
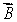
B)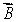 ·
· 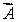
C)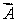
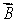
D)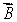
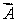
E) None of these is correct.
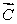 represents
represents 
A)
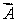
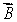
B)
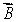 ·
· 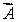
C)
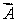
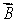
D)
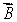
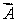
E) None of these is correct.
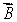
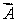
4
A phonograph turntable in the xz plane is rotating clockwise as viewed from above. The vector that represents the torque with which the motor turns the table is 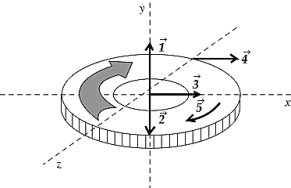
A)
B)
C)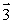
D)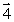
E)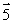

A)
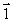
B)
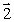
C)
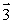
D)
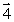
E)
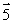

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
5
Large meteors can impact the earth with speeds of 80,000 km/h. If such a meteor were to impact at a point on the plane of Earth's equator, resulting in a change of Earth's angular momentum by 80 × 1012 kg • m2/s (an insignificant change, thankfully), calculate the mass of the meteor. (The radius of Earth = 6.38 106 m.)
A) 3.4 104 kg
B) 5.6 102 kg
C) 3.6 103 kg
D) 4.5 104 kg
E) 56 kg
A) 3.4 104 kg
B) 5.6 102 kg
C) 3.6 103 kg
D) 4.5 104 kg
E) 56 kg

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
6
A force  x in the negative x direction is applied to a particle in the xy plane. The arrow that best represents the torque produced by
x in the negative x direction is applied to a particle in the xy plane. The arrow that best represents the torque produced by 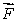 x on the particle with respect to the origin is
x on the particle with respect to the origin is 
A)
B)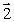
C)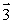
D)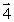
E)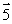
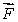 x in the negative x direction is applied to a particle in the xy plane. The arrow that best represents the torque produced by
x in the negative x direction is applied to a particle in the xy plane. The arrow that best represents the torque produced by 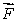 x on the particle with respect to the origin is
x on the particle with respect to the origin is 
A)
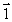
B)
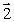
C)
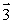
D)
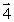
E)
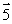

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
7
The angular momentum of a system is conserved only if
A) the angular velocity is a function of time.
B) the sum of the external torques equals the sum of the internal torques.
C) the moment of inertia of the system is constant.
D) the sum of the external torques is zero.
E) the sum of the internal torques is zero.
A) the angular velocity is a function of time.
B) the sum of the external torques equals the sum of the internal torques.
C) the moment of inertia of the system is constant.
D) the sum of the external torques is zero.
E) the sum of the internal torques is zero.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
8
Let us compare the angular momentum of Mars (LM) in its orbit around the Sun to that of Earth (LE). The mean orbital speed of Mars is 24 km/s, whereas that of Earth is 30 km/s. The mean orbital radius of Mars is 228 106 km, whereas that of Earth is 150 106 km. If the mass of Mars is 11% that of Earth, calculate the ratio LM / LE.
A) 0.21
B) 0.090
C) 7.7
D) 11
E) 0.13
A) 0.21
B) 0.090
C) 7.7
D) 11
E) 0.13

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
9
The angular momentum of a flywheel about its axis is 925 kg · m2/s. If its moment of inertia about the same axis is 2.50 kg · m2, its angular velocity is
A) 370 rev/min
B) 62 rev/min
C) 36 rev/min
D) 2210 rad/s
E) 370 rad/s
A) 370 rev/min
B) 62 rev/min
C) 36 rev/min
D) 2210 rad/s
E) 370 rad/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
10
Vectors 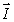 and
and 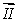 lie in the xy plane. The vector product
lie in the xy plane. The vector product 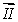 (
( 
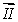 ) could be represented by vector
) could be represented by vector 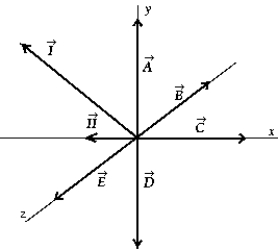
A)
B)
C)
D)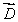
E)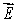
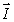 and
and 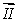 lie in the xy plane. The vector product
lie in the xy plane. The vector product 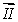 (
( 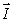
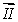 ) could be represented by vector
) could be represented by vector 
A)
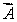
B)
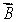
C)
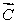
D)
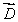
E)
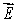

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
11
A wheel is rotating clockwise on a fixed axis perpendicular to the page (x). A torque that causes the wheel to slow down is best represented by the vector 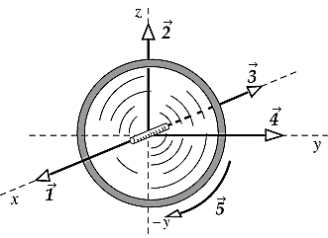
A)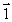
B)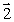
C)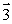
D)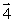
E)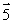

A)
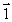
B)
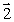
C)
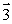
D)
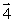
E)
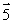

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
12
Particles 1, 2, and 3 have equal masses and equal speeds. The angular momentum with respect to the origin for these three masses is 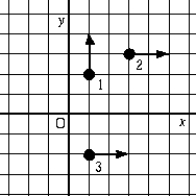
A) the same for each particle.
B) greatest for particle 1.
C) greatest for particle 2.
D) greatest for particle 3.
E) least for particle 2.

A) the same for each particle.
B) greatest for particle 1.
C) greatest for particle 2.
D) greatest for particle 3.
E) least for particle 2.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
13
A disc rotates clockwise in the plane of the page. What is the direction of the angular momentum vector?
A) clockwise
B) counterclockwise
C) into the page
D) out of the page
E) angular momentum has no direction
A) clockwise
B) counterclockwise
C) into the page
D) out of the page
E) angular momentum has no direction

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
14
Coriolis acceleration is a result of fictitious force when an observer is in a rotating frame. It is expressed as 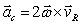 where
where 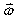 is the angular velocity of the rotating frame and
is the angular velocity of the rotating frame and  is the velocity of an object in the rotating frame. Suppose
is the velocity of an object in the rotating frame. Suppose 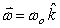 and
and 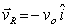 what is
what is 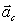 ?
?
A)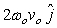
B)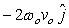
C)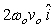
D)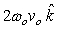
E) None of these is correct.
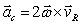 where
where 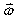 is the angular velocity of the rotating frame and
is the angular velocity of the rotating frame and  is the velocity of an object in the rotating frame. Suppose
is the velocity of an object in the rotating frame. Suppose 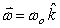 and
and 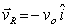 what is
what is 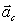 ?
?A)
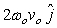
B)
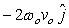
C)
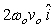
D)
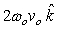
E) None of these is correct.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
15
As a particle with a velocity 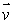 in the negative x direction passes through the point (0, 0, 1), it has an angular velocity relative to the origin that is best represented by vector
in the negative x direction passes through the point (0, 0, 1), it has an angular velocity relative to the origin that is best represented by vector 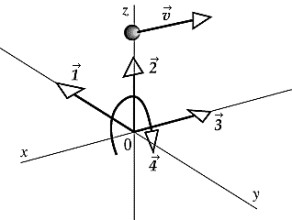
A)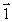
B)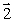
C)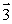
D)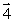
E) zero
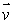 in the negative x direction passes through the point (0, 0, 1), it has an angular velocity relative to the origin that is best represented by vector
in the negative x direction passes through the point (0, 0, 1), it has an angular velocity relative to the origin that is best represented by vector 
A)
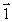
B)
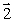
C)
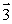
D)
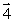
E) zero

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
16
The angular momentum of a rotating object is initially 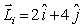 and 2s later it is
and 2s later it is 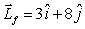 . The units are in kg.m2/s. The torque that produces the change in angular momentum is
. The units are in kg.m2/s. The torque that produces the change in angular momentum is
A)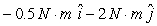
B)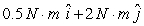
C)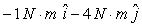
D)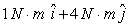
E) none of the above
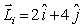 and 2s later it is
and 2s later it is 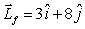 . The units are in kg.m2/s. The torque that produces the change in angular momentum is
. The units are in kg.m2/s. The torque that produces the change in angular momentum isA)
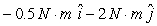
B)
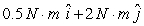
C)
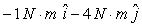
D)
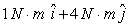
E) none of the above

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
17
A particle of mass m is moving with a velocity 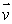 , in the yz plane as shown. The vector that most nearly represents the angular momentum about the x axis is
, in the yz plane as shown. The vector that most nearly represents the angular momentum about the x axis is 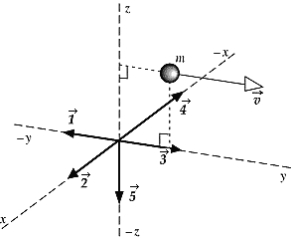
A)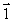
B)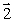
C)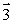
D)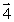
E)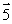
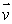 , in the yz plane as shown. The vector that most nearly represents the angular momentum about the x axis is
, in the yz plane as shown. The vector that most nearly represents the angular momentum about the x axis is 
A)
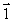
B)
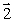
C)
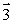
D)
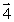
E)
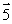

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
18
A 7-kg mass and a 4-kg mass are mounted on a spindle that is free to turn about the x axis as shown. Assume the mass of the arms and the spindle to be negligible. If the system is free to rotate and is released from rest, there will initially be a resultant torque in which of the following directions? 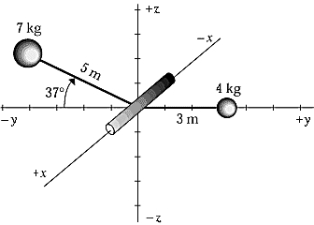
A) z
B) -z
C) y
D) -x
E) x

A) z
B) -z
C) y
D) -x
E) x

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
19
A torque is applied to a bolt by hanging a weight w from the end of the wrench, as shown. The coordinate axis along which the torque vector is directed is 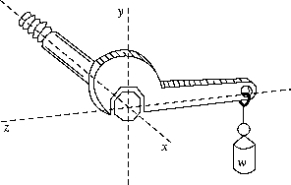
A) y
B) x
C) -y
D) -x
E) z

A) y
B) x
C) -y
D) -x
E) z

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
20
If the angular momentum of a system is constant, which of the following statements must be true?
A) No torque acts on any part of the system.
B) A constant torque acts on each part of the system.
C) Zero net torque acts on each part of the system.
D) A constant external torque acts on the system.
E) Zero net torque acts on the system.
A) No torque acts on any part of the system.
B) A constant torque acts on each part of the system.
C) Zero net torque acts on each part of the system.
D) A constant external torque acts on the system.
E) Zero net torque acts on the system.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
21
The angular momentum vector for a spinning wheel lies along its axle and is pointed east. To make this vector point south, it is necessary to exert a force on the east end of the axle in which direction?
A) up
B) down
C) north
D) south
E) east
A) up
B) down
C) north
D) south
E) east

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
22
A man stands on the center of a platform that is rotating on frictionless bearings at a speed of 1.00 rad/s. Originally his arms are outstretched and he holds a 4.54-kg mass in each hand. He then pulls the weights in toward his body. Assume the moment of inertia of the man, including his arms, to remain constant at 5.42 kg · m2. If the original distance of the weights from the axis is 0.914 m and their final distance is 0.305 m, the final angular velocity is
A) 1.14 rad/s
B) 1.27 rad/s
C) 1.58 rad/s
D) 2.08 rad/s
E) 7.70 rad/s
A) 1.14 rad/s
B) 1.27 rad/s
C) 1.58 rad/s
D) 2.08 rad/s
E) 7.70 rad/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
23
A hoop rotates about an axis through its center with an angular velocity of 40.0 rad/s. If the rotational kinetic energy of the hoop is 400 J, its angular momentum is
A) 800 kg · m2/s
B) 400 kg · m2/s
C) 200 kg · m2/s
D) 20 kg · m2/s
E) 5 kg · m2/s
A) 800 kg · m2/s
B) 400 kg · m2/s
C) 200 kg · m2/s
D) 20 kg · m2/s
E) 5 kg · m2/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
24
If the sum of the external torques acting on an isolated system of particles is zero, it must be true that
A) the system can have no kinetic energy.
B) the angular momentum of the system does not change.
C) the system can have no angular velocity.
D) the system can have no linear velocity.
E) the angular momentum of the system must be continually decreasing.
A) the system can have no kinetic energy.
B) the angular momentum of the system does not change.
C) the system can have no angular velocity.
D) the system can have no linear velocity.
E) the angular momentum of the system must be continually decreasing.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
25
A man turns with an angular velocity on a rotating table, holding two equal masses at arms' length. If he drops the two masses without moving his arms, his angular velocity
A) decreases.
B) remains the same.
C) increases.
D) increases as the angular velocity of the masses decreases.
E) decreases as the angular velocity of the masses increases.
A) decreases.
B) remains the same.
C) increases.
D) increases as the angular velocity of the masses decreases.
E) decreases as the angular velocity of the masses increases.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
26
A disc-shaped grindstone of mass 3.0 kg and radius 8.0 cm is spinning at 600 rev/min. After the power is shut off, a man continues to sharpen his axe by holding it against the grindstone until it stops 10 s later. What was the stone's initial kinetic energy when the power was turned off?
A) 19 J
B) 3.8 10-3 J
C) 4.8 10-5 J
D) 1.9 10-3 J
E) 2.4 10-2 J
A) 19 J
B) 3.8 10-3 J
C) 4.8 10-5 J
D) 1.9 10-3 J
E) 2.4 10-2 J

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
27
A wheel is rotating freely with an angular speed of 20 rad/s on a shaft whose moment of inertia is negligible. A second identical wheel, initially at rest, is suddenly coupled to the same shaft. The angular speed of the coupled wheels is
A) 10 rad/s
B) 14 rad/s
C) 20 rad/s
D) 28 rad/s
E) 40 rad/s
A) 10 rad/s
B) 14 rad/s
C) 20 rad/s
D) 28 rad/s
E) 40 rad/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
28
A woman sits on a stool that can turn friction-free about its vertical axis. She is handed a spinning bicycle wheel that has angular momentum 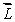 0 and she turns it over (that is, through 180º). She thereby acquires an angular momentum of magnitude
0 and she turns it over (that is, through 180º). She thereby acquires an angular momentum of magnitude 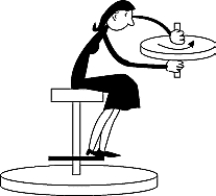
A) 0
B)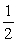
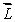 0
0
C)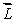 0
0
D) 2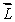 0
0
E) 4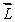 0
0
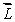 0 and she turns it over (that is, through 180º). She thereby acquires an angular momentum of magnitude
0 and she turns it over (that is, through 180º). She thereby acquires an angular momentum of magnitude 
A) 0
B)
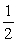
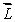 0
0 C)
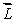 0
0 D) 2
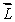 0
0E) 4
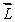 0
0 
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
29
A merry-go-round with a moment of inertia of 6.78 103 kg · m2 is coasting at 2.20 rad/s. When a 72.6-kg man steps onto the rim, the angular velocity decreases to 2.0 rad/s. The radius of the merry-go-round is
A) 3.06 m
B) 3.66 m
C) 4.27 m
D) 4.88 m
E) 5.49 m
A) 3.06 m
B) 3.66 m
C) 4.27 m
D) 4.88 m
E) 5.49 m

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
30
The velocity a planet of mass m with circular orbit is given by 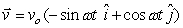 where vo in m/s is a constant, and is the angular velocity. Its position vector is
where vo in m/s is a constant, and is the angular velocity. Its position vector is 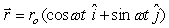 .The angular momentum of the planet about the center of the orbit is
.The angular momentum of the planet about the center of the orbit is
A) mvoro
mvoro 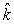
B) mvoro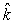
C) mvoro (2 sin t cos t)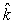
D) mvoro (2 sin t cos t)
mvoro (2 sin t cos t) 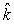
E) none of the above
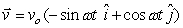 where vo in m/s is a constant, and is the angular velocity. Its position vector is
where vo in m/s is a constant, and is the angular velocity. Its position vector is 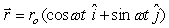 .The angular momentum of the planet about the center of the orbit is
.The angular momentum of the planet about the center of the orbit isA)
 mvoro
mvoro 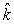
B) mvoro
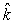
C) mvoro (2 sin t cos t)
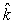
D)
 mvoro (2 sin t cos t)
mvoro (2 sin t cos t) 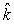
E) none of the above

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
31
The angular momentum of a body about a particular axis as a function of time is shown in the graph. The external torque acting on the body along this axis at t = 2 s is 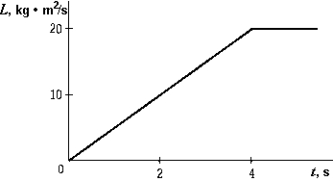
A) 0
B) 5 N · m
C) 10 N · m
D) 20 N · m
E) 40 N · m

A) 0
B) 5 N · m
C) 10 N · m
D) 20 N · m
E) 40 N · m

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
32
In a playground there is a small merry-go-round of radius 1.25 m and mass 175 kg. Assume the merry-go-round to be a uniform disc. A child of mass 45 kg runs at a speed of 3.0 m/s tangent to the rim of the merry-go-round (initially at rest) and jumps on. If we neglect friction, what is the angular speed of the merry-go-round after the child has jumped on and is standing at its outer rim?
A) 0.82 rad/s
B) 2.4 rad/s
C) 0.49 rad/s
D) 1.2 rad/s
E) 0.41 rad/s
A) 0.82 rad/s
B) 2.4 rad/s
C) 0.49 rad/s
D) 1.2 rad/s
E) 0.41 rad/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
33
If the sum of the torques on a body about a fixed axis is not zero, the body most certainly
A) experiences translational acceleration.
B) experiences angular acceleration.
C) experiences precession.
D) experiences rotational inertia.
E) remains in equilibrium.
A) experiences translational acceleration.
B) experiences angular acceleration.
C) experiences precession.
D) experiences rotational inertia.
E) remains in equilibrium.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
34
An athletic can twirl a baton so that it reaches an angular velocity of 12 rad/s from rest in 0.5 s. If the length of a uniform baton is 0.8 m and the mass is 0.5 kg, what is the torque needed to reach the angular velocity?
A) 0.4 N.m
B) 0.5 N.m
C) 0.8 N.m
D) 0.64 N.m
E) 1.24 N.m
A) 0.4 N.m
B) 0.5 N.m
C) 0.8 N.m
D) 0.64 N.m
E) 1.24 N.m

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
35
A constant torque of 15 N · m acts for 3.0 s on a system of mass 2.0 kg. The change in angular momentum of the system during this period of time is
A) 5.0 kg · m2/s
B) 7.5 kg · m2/s
C) 10 kg · m2/s
D) 23 kg · m2/s
E) 45 kg · m2/s
A) 5.0 kg · m2/s
B) 7.5 kg · m2/s
C) 10 kg · m2/s
D) 23 kg · m2/s
E) 45 kg · m2/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
36
A spinning bicycle wheel is supported as shown by a line fastened to one end of its axle. The resultant torque acting on the wheel lies along which of the following axes? 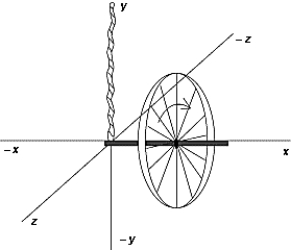
A) x
B) y
C) -y
D) z
E) -z

A) x
B) y
C) -y
D) z
E) -z

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
37
A woman sits on a spinning piano stool with her arms folded. When she extends her arms, which of the following occurs?
A) She increases her moment of inertia, thereby increasing her angular speed.
B) She increases her moment of inertia, thereby decreasing her angular speed.
C) She decreases her moment of inertia, thereby increasing her angular speed.
D) She decreases her moment of inertia, thereby decreasing her angular speed.
E) Both her moment of inertia and her angular speed remain constant.
A) She increases her moment of inertia, thereby increasing her angular speed.
B) She increases her moment of inertia, thereby decreasing her angular speed.
C) She decreases her moment of inertia, thereby increasing her angular speed.
D) She decreases her moment of inertia, thereby decreasing her angular speed.
E) Both her moment of inertia and her angular speed remain constant.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
38
Two identical cylindrical discs have a common axis. Initially one of the discs is spinning. When the two discs are brought into contact, they stick together. Which of the following is true?
A) The total kinetic energy and the total angular momentum are unchanged from their initial values.
B) Both the total kinetic energy and the total angular momentum are reduced to half of their original values.
C) The total angular momentum is unchanged, but the total kinetic energy is reduced to half its original value.
D) The total angular momentum is reduced to half its original value, but the total kinetic energy is unchanged.
E) The total angular momentum is unchanged, and the total kinetic energy is reduced to one-quarter of its original value.
A) The total kinetic energy and the total angular momentum are unchanged from their initial values.
B) Both the total kinetic energy and the total angular momentum are reduced to half of their original values.
C) The total angular momentum is unchanged, but the total kinetic energy is reduced to half its original value.
D) The total angular momentum is reduced to half its original value, but the total kinetic energy is unchanged.
E) The total angular momentum is unchanged, and the total kinetic energy is reduced to one-quarter of its original value.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
39
If the sum of the external torques on a system is zero, there is
A) a change in the system's moment of inertia.
B) no change in the system's moment of inertia.
C) a change in the system's angular momentum.
D) no change in the system's angular momentum.
E) a precessional angular velocity.
A) a change in the system's moment of inertia.
B) no change in the system's moment of inertia.
C) a change in the system's angular momentum.
D) no change in the system's angular momentum.
E) a precessional angular velocity.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
40
Two balls, each of mass m, are attached to the ends of a rod of length l and mass M. The system is then rotated about a frictionless pivot located at the center of mass with angular velocity . The angular momentum of the system in vector form about the pivot is 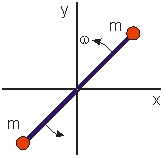
A)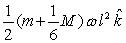
B)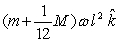
C)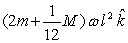
D)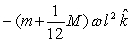
E) none of the above

A)
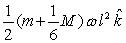
B)
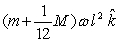
C)
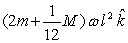
D)
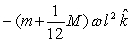
E) none of the above

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
41
A gyroscopic wheel spins clockwise as shown. The set of vectors that correctly describes the directions of the torque 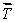 , angular momentum
, angular momentum 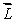 , and angular velocity of precession
, and angular velocity of precession 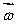 p, is
p, is 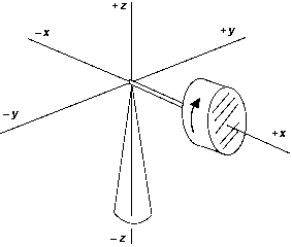
A)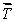 (+z);
(+z); 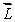 (-x);
(-x); 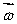 (+y)
(+y)
B)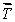 (-z);
(-z); 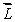 (+x);
(+x); 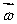 (-y)
(-y)
C)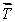 (+y);
(+y); 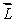 (-x);
(-x); 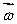 (+z)
(+z)
D)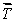 (-y);
(-y); 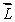 (-z);
(-z); 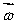 (-x)
(-x)
E)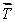 (+y);
(+y); 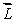 (-x);
(-x); 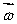 (-z)
(-z)
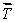 , angular momentum
, angular momentum 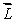 , and angular velocity of precession
, and angular velocity of precession 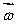 p, is
p, is 
A)
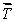 (+z);
(+z); 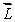 (-x);
(-x); 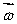 (+y)
(+y)B)
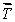 (-z);
(-z); 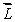 (+x);
(+x); 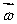 (-y)
(-y)C)
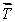 (+y);
(+y); 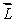 (-x);
(-x); 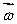 (+z)
(+z)D)
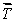 (-y);
(-y); 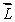 (-z);
(-z); 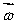 (-x)
(-x)E)
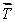 (+y);
(+y); 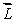 (-x);
(-x); 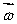 (-z)
(-z)
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
42
The propeller of a motorboat turns clockwise relative to a water skier being towed by the boat. As the boat makes a sharp turn to the left, gyroscopic action tends to
A) cause the front of the boat to rise.
B) cause the front of the boat to dip.
C) cause the boat to tip to the left.
D) cause the boat to tip to the right.
E) keep the boat headed in its original direction.
A) cause the front of the boat to rise.
B) cause the front of the boat to dip.
C) cause the boat to tip to the left.
D) cause the boat to tip to the right.
E) keep the boat headed in its original direction.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
43
Spin  particles
particles
A) are called bosons.
B) have spin angular momenta that can be changed by applying a net torque to them.
C) can have angular momenta that change continuously from one value to another.
D) can very accurately be thought of as spinning spheres.
E) are described by none of the above.
 particles
particlesA) are called bosons.
B) have spin angular momenta that can be changed by applying a net torque to them.
C) can have angular momenta that change continuously from one value to another.
D) can very accurately be thought of as spinning spheres.
E) are described by none of the above.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
44
A wheel of moment of inertia 0.136 kg · m2 is spinning with an angular speed of 5000 rad/s. A torque is applied about an axis perpendicular to the spin axis. If the applied torque has a magnitude of 67.8 N · m, the angular velocity of precession will be
A) 1.00 rad/s
B) 0.100 rad/s
C) 10.0 rad/s
D) 100 rad/s
E) 1000 rad/s
A) 1.00 rad/s
B) 0.100 rad/s
C) 10.0 rad/s
D) 100 rad/s
E) 1000 rad/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
45
A certain airplane engine rotates counterclockwise when viewed from aft (that is, from the back of the airplane). When the plane turns to the left,
A) the engine makes it turn faster than when it turns to the right.
B) the engine makes it turn slower than when it turns to the right.
C) it tends to dive.
D) it tends to climb.
E) the engine has no effect on the turn.
A) the engine makes it turn faster than when it turns to the right.
B) the engine makes it turn slower than when it turns to the right.
C) it tends to dive.
D) it tends to climb.
E) the engine has no effect on the turn.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
46
If an object were to suddenly shrink and decrease its moment of inertia by a factor of 3, what is the difference in energy between the final and initial rotational kinetic energies?
A) 3 times initial Krot
B) 9 times initial Krot
C) 8 times initial Krot
D) 2 times initial Krot
E) zero, Krot remains the same
A) 3 times initial Krot
B) 9 times initial Krot
C) 8 times initial Krot
D) 2 times initial Krot
E) zero, Krot remains the same

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
47
A spinning bicycle wheel with a loaded rim (essentially a hoop) is supported by a line at one end of its axle. The radius of the wheel is 0.305 m, and the wheel has a mass of 3.63 kg. It is spinning at 80.0 rad/s, and the center of mass is 15.2 cm from the point of support. The angular velocity of precession is
A) 0.0125 rad/s
B) 0.0318 rad/s
C) 0.200 rad/s
D) 0.100 rad/s
E) 0.625 rad/s
A) 0.0125 rad/s
B) 0.0318 rad/s
C) 0.200 rad/s
D) 0.100 rad/s
E) 0.625 rad/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
48
A disc with moment of inertia I1 = 40 kg.m2 and angular velocity 1 = 20 rad/s is dropped on to a stationary second disc along the axis of rotation. The second disc has moment of inertia I2 = 60 kg.m2. How much rotational kinetic energy is lost?
A) 3200 J
B) 4800 J
C) 8000 J
D) 11300 J
E) 15000 J
A) 3200 J
B) 4800 J
C) 8000 J
D) 11300 J
E) 15000 J

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
49
A man is walking north carrying a suitcase that contains a spinning gyroscope mounted on an axle attached to the front and back of the case. The angular velocity of the gyroscope points north. The man now begins to turn to walk east. As a result, the front end of the suitcase 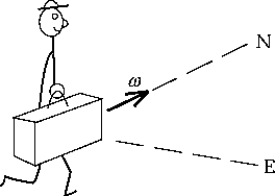
A) resists his attempt to turn and tries to remain pointed north.
B) fights his attempt to turn and pulls to the west.
C) rises upward.
D) dips downward.
E) does nothing whatever unusual.

A) resists his attempt to turn and tries to remain pointed north.
B) fights his attempt to turn and pulls to the west.
C) rises upward.
D) dips downward.
E) does nothing whatever unusual.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
50
Two wheels with identical moments of inertia are rotating about the same axle. The first is rotating clockwise at 2.0 rad/s, and the second is rotating counterclockwise at 6.0 rad/s. If the two wheels are brought into contact so that they rotate together, their final angular velocity will be
A) 2.0 rad/s, counterclockwise.
B) 3.0 rad/s, clockwise.
C) 4.0 rad/s, counterclockwise.
D) 5.0 rad/s, clockwise.
E) 6.0 rad/s, clockwise.
A) 2.0 rad/s, counterclockwise.
B) 3.0 rad/s, clockwise.
C) 4.0 rad/s, counterclockwise.
D) 5.0 rad/s, clockwise.
E) 6.0 rad/s, clockwise.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
51
Which of the following statements is true?
A) The angular momentum of a particle due to its motion is its orbital angular momentum.
B) Spin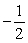 particles are called fermions.
particles are called fermions.
C) The fundamental unit of angular momentum is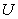 .
.
D) The units of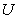 are J·s.
are J·s.
E) All of these are correct.
A) The angular momentum of a particle due to its motion is its orbital angular momentum.
B) Spin
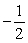 particles are called fermions.
particles are called fermions.C) The fundamental unit of angular momentum is
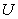 .
.D) The units of
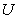 are J·s.
are J·s.E) All of these are correct.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
52
A disc with moment of inertia I1 = 40 kg.m2 and angular velocity 1 = 20 rad/s is dropped on to a stationary second disc along the axis of rotation. The second disc has moment of inertia I2 = 60 kg.m2. What is the angular velocity of the two discs?
A) 4 rad/s
B) 6 rad/s
C) 8 rad/s
D) 12 rad/s
E) 20 rad/s
A) 4 rad/s
B) 6 rad/s
C) 8 rad/s
D) 12 rad/s
E) 20 rad/s

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
53
Use the figure to the right to answer the next problem.
A ball of mass of mass m is tied with a light string to a vertical post of radius Rp and slides on a frictionless horizontal surface. As the ball travels around the post, the string wraps around the post, shortening the length. At t = 0 s, its speed is vo and radius is ro.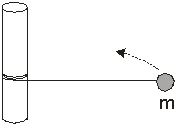
-As the string wraps around the post, which of the following statements is true?
A) Angular momentum is conserved but not the mechanical energy.
B) Angular momentum is not conserved but the mechanical energy is conserved.
C) Both the angular momentum and the mechanical energy are conserved.
D) Angular momentum increases as the string gets shorter.
E) Whether the angular momentum and mechanical energy are conserved depends on vo and ro.
A ball of mass of mass m is tied with a light string to a vertical post of radius Rp and slides on a frictionless horizontal surface. As the ball travels around the post, the string wraps around the post, shortening the length. At t = 0 s, its speed is vo and radius is ro.

-As the string wraps around the post, which of the following statements is true?
A) Angular momentum is conserved but not the mechanical energy.
B) Angular momentum is not conserved but the mechanical energy is conserved.
C) Both the angular momentum and the mechanical energy are conserved.
D) Angular momentum increases as the string gets shorter.
E) Whether the angular momentum and mechanical energy are conserved depends on vo and ro.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
54
A wheel is rotating in the direction indicated. If you pull down on the end of the axle nearest you, that end of the axle tends to move 
A) up.
B) to the right.
C) down.
D) to the left.
E) directly inward.

A) up.
B) to the right.
C) down.
D) to the left.
E) directly inward.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
55
Consider Earth as a uniform sphere of diameter 12.7 106 m, with a mass of the 5.98 1030 kg, and a rotational period of 1 day. If Earth suddenly had a diameter of half this value without any loss of mass, calculate the new period of rotation.
A) 0.5 days
B) 2.0 days
C) 0.25 days
D) 4.0 days
E) 1.4 days
A) 0.5 days
B) 2.0 days
C) 0.25 days
D) 4.0 days
E) 1.4 days

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
56
The figure shows vectors representing the angular velocity of precession p and the spin velocity s. The associated torque vector points along which of the axes? 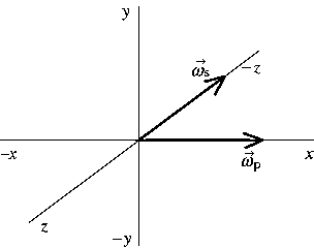
A) -x
B) y
C) z
D) -z
E) None of these is correct.

A) -x
B) y
C) z
D) -z
E) None of these is correct.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
57
A solid cylinder is spinning counterclockwise about a longitudinal axis when a net torque is applied, as shown. The cylinder 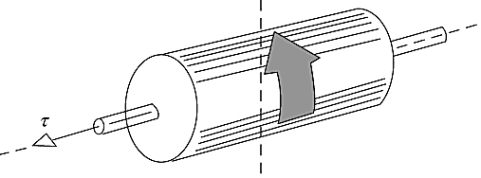
A) speeds up.
B) slows down.
C) precesses about a vertical axis.
D) precesses about a horizontal axis.
E) does none of these.

A) speeds up.
B) slows down.
C) precesses about a vertical axis.
D) precesses about a horizontal axis.
E) does none of these.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
58
A wheel is set spinning and then is hung by a rope placed at one end of the axle. The precession vector of the spinning wheel points in the direction of 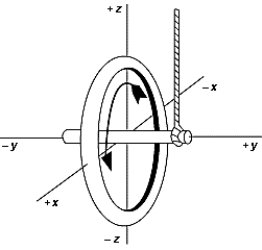
A) z
B) -y
C) -z
D) -x
E) y

A) z
B) -y
C) -z
D) -x
E) y

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
59
Use the figure to the right to answer the next problem.
A ball of mass of mass m is tied with a light string to a vertical post of radius Rp and slides on a frictionless horizontal surface. As the ball travels around the post, the string wraps around the post, shortening the length. At t = 0 s, its speed is vo and radius is ro.
-What is the angular momentum of the ball after the string has wrapped once around the post?
A)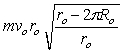
B)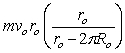
C)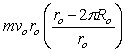
D)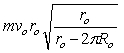
E) cannot be determined
A ball of mass of mass m is tied with a light string to a vertical post of radius Rp and slides on a frictionless horizontal surface. As the ball travels around the post, the string wraps around the post, shortening the length. At t = 0 s, its speed is vo and radius is ro.

-What is the angular momentum of the ball after the string has wrapped once around the post?
A)
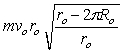
B)
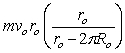
C)
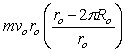
D)
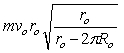
E) cannot be determined

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
60
Which of the following are required for the total momentum (both angular and linear) of a system to be conserved?
1.The sum of the external torques acting on the system must be zero.
2.The sum of the external forces acting on the system must be zero.
3.The total kinetic energy must remain constant.
4.There can be no external torques or forces acting on the system.
5.There can be no internal torques or forces acting on the system.
A)1 and 2
B)1, 2, and 3
C)1, 2, and 4
D)1, 2, 3, and 4
E)1, 2, 3, 4, and 5
1.The sum of the external torques acting on the system must be zero.
2.The sum of the external forces acting on the system must be zero.
3.The total kinetic energy must remain constant.
4.There can be no external torques or forces acting on the system.
5.There can be no internal torques or forces acting on the system.
A)1 and 2
B)1, 2, and 3
C)1, 2, and 4
D)1, 2, 3, and 4
E)1, 2, 3, 4, and 5

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
61
Which of the following statements is not true?
A) Stable matter consists of electrons, protons, and neutrons.
B) Electrons, protons, and neutrons have an intrinsic angular momentum that is called spin.
C) Bosons have zero spin or integral spin.
D) An electron is well known to have a finite size.
E) The spin angular momentum of a particle is a fundamental property of the particle and as such cannot be changed.
A) Stable matter consists of electrons, protons, and neutrons.
B) Electrons, protons, and neutrons have an intrinsic angular momentum that is called spin.
C) Bosons have zero spin or integral spin.
D) An electron is well known to have a finite size.
E) The spin angular momentum of a particle is a fundamental property of the particle and as such cannot be changed.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
62
If the distance between two hydrogen atoms of H2 is 0.1 nm, what is its E0r?
A) 2.40 10-23 J
B) 6.70 10-22 J
C) 1.05 10-22 J
D) 1.60 10-22 J
E) 2.45 10-22 J
A) 2.40 10-23 J
B) 6.70 10-22 J
C) 1.05 10-22 J
D) 1.60 10-22 J
E) 2.45 10-22 J

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
63
In a rotating atomic nucleus shaped like a football the quantized energy levels have rotational quantum number values of 0, 2, 4, etc. If the energies of the first three states are 0 keV, 138 keV, and 460 keV, calculate the moment of inertia of the nucleus.
A) 9.41 10-36 keV•s2
B) 9.41 10-36 eV•s2
C) 1.43 10-17 keV•s2
D) 1.43 10-17 eV•s2
E) 9.41 10-33 keV•s2
A) 9.41 10-36 keV•s2
B) 9.41 10-36 eV•s2
C) 1.43 10-17 keV•s2
D) 1.43 10-17 eV•s2
E) 9.41 10-33 keV•s2

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
64
Which of the following statements is true?
A) Stable matter consists of electrons, protons, and neutrons.
B) Electrons, protons, and neutrons have an intrinsic angular momentum that is called spin.
C) Bosons have zero spin or integral spin.
D) The spin angular momentum of a particle is a fundamental property of the particle and as such cannot be changed.
E) All of these are correct.
A) Stable matter consists of electrons, protons, and neutrons.
B) Electrons, protons, and neutrons have an intrinsic angular momentum that is called spin.
C) Bosons have zero spin or integral spin.
D) The spin angular momentum of a particle is a fundamental property of the particle and as such cannot be changed.
E) All of these are correct.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
65
In a rotating atomic nucleus shaped like a football the quantized rotational energy levels have angular momentum values l = 0, 2, 4, 6, 8, etc. Given that the energy of each level is equal to a constant times l (l + 1), calculate the ratio of the l = 4 to l = 2 energy levels.
A) 4.0
B) 0.3
C) 2.0
D) 0.5
E) 3.3
A) 4.0
B) 0.3
C) 2.0
D) 0.5
E) 3.3

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
66
For a rotating molecule with a constant moment of inertia what is the energy difference between the l = 5 and l = 7 energy levels?
A) 2 E0r
B) 24 E0r
C) 86 E0r
D) 26 E0r
E) 35 E0r
A) 2 E0r
B) 24 E0r
C) 86 E0r
D) 26 E0r
E) 35 E0r

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
67
The energy-level diagram that most closely represents a rotating molecule with constant moment of inertia is 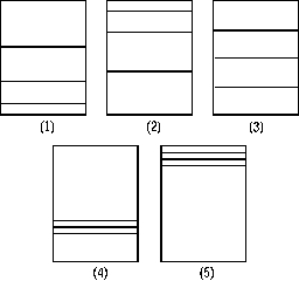
A) 1
B) 2
C) 3
D) 4
E) 5

A) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck


