Deck 10: Introducing Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/66
Play
Full screen (f)
Deck 10: Introducing Probability
1
A randomly selected sample of 100 horse owners found that 72 of them feed two flakes of grass hay in the morning and one flake of alfalfa plus one flake of grass hay in the evening to their horses. The estimated probability that horse owners feed grass hay in the morning and alfalfa plus grass hay in the evening is:
A)0.72.
B)0.75.
C)0.5.
D)0.25.
A)0.72.
B)0.75.
C)0.5.
D)0.25.
0.72.
2
A North American roulette wheel has 38 slots, of which 18 are red, 18 are black, and 2 are green. If you bet on red, the probability of winning is 18/38 = 0.4737. The probability 0.4737 represents:
A)the fact that you are more likely to win betting on red than you are to lose.
B)the proportion of times this event will occur in a very long series of individual bets on red.
C)the fact that if you make 100 wagers on red, you will have 47 or 48 wins.
D)nothing important, because every spin of the wheel results in one of three outcomes (red, black, or green).
A)the fact that you are more likely to win betting on red than you are to lose.
B)the proportion of times this event will occur in a very long series of individual bets on red.
C)the fact that if you make 100 wagers on red, you will have 47 or 48 wins.
D)nothing important, because every spin of the wheel results in one of three outcomes (red, black, or green).
the proportion of times this event will occur in a very long series of individual bets on red.
3
An assignment of probabilities to events in a sample space must obey which of the following?
A)The probability of any event must be a number between 0 and 1, inclusive.
B)They must sum to 1 when adding over all events in the sample space.
C)They must obey the addition rule for disjoint events.
D)All of the answer options are correct.
A)The probability of any event must be a number between 0 and 1, inclusive.
B)They must sum to 1 when adding over all events in the sample space.
C)They must obey the addition rule for disjoint events.
D)All of the answer options are correct.
All of the answer options are correct.
4
An urn contains 2 red and 2 green marbles. We pick a marble, record its color, and replace it. We repeat this procedure a second and a third time. The probability distribution for the number of red marbles is given by:
A)
B)
C)
D)
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
5
A randomly selected sample of 100 horse owners found that 72 of them feed one flake of alfalfa plus one flake of grass hay in the evening to their horses, while the rest feed one flake of alfalfa plus oat hay in the evening. The estimated probability that horse owners feed alfalfa plus oat hay in the evening is:
A)0.72.
B)0.5.
C)0.28.
D)0.75.
A)0.72.
B)0.5.
C)0.28.
D)0.75.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
6
When we draw a card from a deck, the outcome is uncertain. The card's value is:
A)random.
B)predictable.
C)deterministic.
D)None of the answer options is correct.
A)random.
B)predictable.
C)deterministic.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
7
Assume that you are about to buy a car. There is a probability of 0.4 that you will purchase a new vehicle, and a probability of 0.5 that you will purchase a used vehicle. There is no probability that you will go home with more than one vehicle. Which of the following is true?
A)The probability that you will not buy a used vehicle is 0.5.
B)If you buy a new car, then you will not buy a used car.
C)Purchasing a new car and purchasing a used car are disjoint events.
D)All of the answer options are correct.
A)The probability that you will not buy a used vehicle is 0.5.
B)If you buy a new car, then you will not buy a used car.
C)Purchasing a new car and purchasing a used car are disjoint events.
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
8
I roll a four-sided die. The possible outcomes are 1, 2, 3, or 4, depending on the number of spots on the side of the die that is face down. This collection of all possible outcomes is called:
A)a census.
B)the probability.
C)the sample space.
D)the distribution.
A)a census.
B)the probability.
C)the sample space.
D)the distribution.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
9
A fair dice is rolled and the sample space is given as S = {1, 2, 3, 4, 5, 6}. Which of the following statements is true?
A)All outcomes in the sample space S are equally likely.
B)The events A = {even number} and B = {odd number} are equally likely.
C)The events A = {even number} and C = {number less than 4} are equally likely.
D)All of the answer options are correct.
A)All outcomes in the sample space S are equally likely.
B)The events A = {even number} and B = {odd number} are equally likely.
C)The events A = {even number} and C = {number less than 4} are equally likely.
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
10
I toss a penny and observe whether it lands heads up or tails up. Suppose the penny is fair; that is, the probability of heads is 1/2 and the probability of tails is 1/2. This means that:
A)every occurrence of a head must be balanced by a tail in one of the next two or three tosses.
B)if I flip the coin many, many times, the proportion of heads will be approximately 1/2, and this proportion will tend to get closer and closer to 1/2 as the number of tosses increases.
C)regardless of the number of flips, half will be heads and half will be tails.
D)All of the answer options are correct.
A)every occurrence of a head must be balanced by a tail in one of the next two or three tosses.
B)if I flip the coin many, many times, the proportion of heads will be approximately 1/2, and this proportion will tend to get closer and closer to 1/2 as the number of tosses increases.
C)regardless of the number of flips, half will be heads and half will be tails.
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
11
About 64% of boys aged 12 to 15 years regularly play video games. If we select a single boy in this age group, the probability that he regularly plays video games is:
A)about 0.17.
B)about 0.83.
C)about 0.64.
D)None of the answer options is correct.
A)about 0.17.
B)about 0.83.
C)about 0.64.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
12
To say that a coin is fair means that when it is tossed, each of the outcomes (heads or tails) has a 50% probability of occurring. This means that:
A)in the next 6 flips of the coin, exactly 3 of the outcomes will be heads.
B)in the next 6 flips of the coin, at least 3 of the outcomes will be heads.
C)in the next 6000 flips of the coin, approximately 3000 of the outcomes will be heads.
D)in the next 6000 flips of the coin, exactly 3000 of the outcomes will be heads.
A)in the next 6 flips of the coin, exactly 3 of the outcomes will be heads.
B)in the next 6 flips of the coin, at least 3 of the outcomes will be heads.
C)in the next 6000 flips of the coin, approximately 3000 of the outcomes will be heads.
D)in the next 6000 flips of the coin, exactly 3000 of the outcomes will be heads.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
13
An urn contains 2 red and 2 green marbles. We pick a marble, record its color, and replace it. We repeat this procedure a second and a third time. The probability distribution for the number of red marbles is given below.

For this distribution, the probability of exactly one red marble is given by:
A)1/8.
B)3/8.
C)7/8.
D)1/3.

For this distribution, the probability of exactly one red marble is given by:
A)1/8.
B)3/8.
C)7/8.
D)1/3.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
14
A randomly selected sample of 100 horse owners found that 72 of them feed grass hay to their horses in the morning and alfalfa in the evening. The value 0.72 represents:
A)the probability that a randomly selected horse owner will feed grass hay in the morning and alfalfa in the evening.
B)the proportion of horse owners in the sample that feed grass hay in the morning and alfalfa in the evening.
C)the probability that a horse will be fed grass hay in the morning and alfalfa in the evening.
D)All of the answer options are correct.
A)the probability that a randomly selected horse owner will feed grass hay in the morning and alfalfa in the evening.
B)the proportion of horse owners in the sample that feed grass hay in the morning and alfalfa in the evening.
C)the probability that a horse will be fed grass hay in the morning and alfalfa in the evening.
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
15
You toss a thumbtack 100 times and observe that it lands point down 65 times. The proportion of times it landed point down is then 0.65. This proportion represents:
A)the sample proportion of tosses that landed point down in your 100 tosses.
B)the correlation between the number of tosses and the number of times it landed point down.
C)the variance of the number of point-down tosses.
D)the probability that the thumbtack lands point down.
A)the sample proportion of tosses that landed point down in your 100 tosses.
B)the correlation between the number of tosses and the number of times it landed point down.
C)the variance of the number of point-down tosses.
D)the probability that the thumbtack lands point down.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
16
An urn contains 2 red and 2 green marbles. We pick a marble, record its color, and replace it. We repeat this procedure a second and a third time. The probability distribution for the number of red marbles is given below.  For this distribution, the probability of 2 or more red marbles is given by:
For this distribution, the probability of 2 or more red marbles is given by:
A)1/2.
B)3/8.
C)6/8.
D)1/4.
 For this distribution, the probability of 2 or more red marbles is given by:
For this distribution, the probability of 2 or more red marbles is given by:A)1/2.
B)3/8.
C)6/8.
D)1/4.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
17
I flip a coin twice and count the number of heads. Which of the following is a valid assignment of probabilities for the number of heads observed in two flips?
A)
B)
C)
D)All of the answer options are correct.
A)

B)

C)

D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
18
You randomly select 500 students and observe that 85 of them smoke. What is your estimate of the probability that a randomly selected student smokes?
A)0.27
B)0.5, because there are two possible outcomes for every student surveyed (smoke or don't smoke)
C)0.17
D)1.2
A)0.27
B)0.5, because there are two possible outcomes for every student surveyed (smoke or don't smoke)
C)0.17
D)1.2

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
19
A North American roulette wheel has 38 slots, of which 18 are red, 18 are black, and 2 are green. Suppose you decide to bet on red on each of 10 consecutive spins of the roulette wheel. Suppose you lose the first five wagers. Which of the following is true?
A)There should be more spins of red in the next five spins of the wheel, because there weren't any on the first five spins.
B)The wheel is not working properly-it favors outcomes that are not red. Hence, during the next five spins of the wheel, we're likely to continue to see few red outcomes.
C)We're due for a win, so the sixth spin of the wheel is very likely to come up red.
D)The outcomes of the first five spins tell us nothing about what will happen on the next five spins.
A)There should be more spins of red in the next five spins of the wheel, because there weren't any on the first five spins.
B)The wheel is not working properly-it favors outcomes that are not red. Hence, during the next five spins of the wheel, we're likely to continue to see few red outcomes.
C)We're due for a win, so the sixth spin of the wheel is very likely to come up red.
D)The outcomes of the first five spins tell us nothing about what will happen on the next five spins.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
20
According to the Current Population Survey, the following table summarizes probabilities for randomly selecting a full-time student in various age groups: 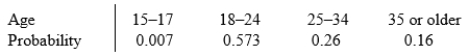 If we randomly select a full-time student, what is the probability that the student is 25 or older?
If we randomly select a full-time student, what is the probability that the student is 25 or older?
A)0.26
B)0.42
C)0.74
D)The answer is impossible to determine from the information given.
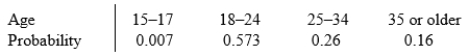 If we randomly select a full-time student, what is the probability that the student is 25 or older?
If we randomly select a full-time student, what is the probability that the student is 25 or older?A)0.26
B)0.42
C)0.74
D)The answer is impossible to determine from the information given.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
21
A basketball player makes 70% of her free throws. When fouled, she gets to take two free throws. Let X represent the number of free throws made in two tries. The probability distribution for the number of free throws she makes in two attempts is summarized in the following table.

The probability that she makes at least one free throw is expressed as:
A)P(X 1).
B)P(X 1).
C)P(X < 1).
D)P(X > 1).

The probability that she makes at least one free throw is expressed as:
A)P(X 1).
B)P(X 1).
C)P(X < 1).
D)P(X > 1).

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
22
The management for a chain of restaurants recorded the number of appetizers, X, ordered by tables dining. They observed that X had the following probability distribution. 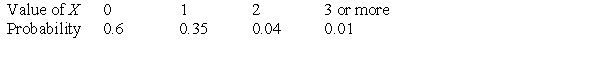 What is P(X < 2)?
What is P(X < 2)?
A)0.04
B)0.35
C)0.6
D)0.95
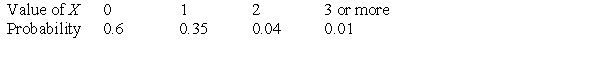 What is P(X < 2)?
What is P(X < 2)?A)0.04
B)0.35
C)0.6
D)0.95

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose we roll two fair four-sided dice. Let X denote the sum of the two roll outcomes. For example, if the first roll yields 3 and the second roll yields 1, then X = 3 + 1 = 4. The probability distribution for X is given below. 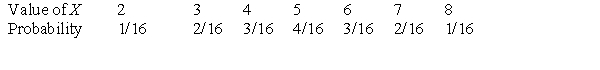 P(X < 5) has the value:
P(X < 5) has the value:
A)1/16.
B)3/16.
C)6/16.
D)10/16.
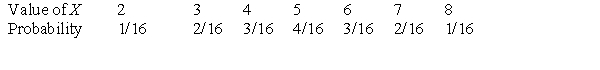 P(X < 5) has the value:
P(X < 5) has the value:A)1/16.
B)3/16.
C)6/16.
D)10/16.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
24
The management for a chain of restaurants recorded the number of appetizers, X, ordered by tables dining. They observed that X had the following probability distribution. 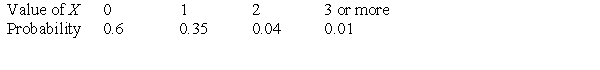 The probability that a randomly chosen table orders at least one appetizer is:
The probability that a randomly chosen table orders at least one appetizer is:
A)0.35.
B)0.39.
C)0.4.
D)None of the answer options is correct.
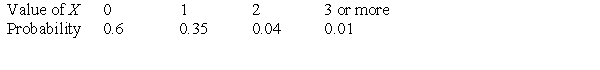 The probability that a randomly chosen table orders at least one appetizer is:
The probability that a randomly chosen table orders at least one appetizer is:A)0.35.
B)0.39.
C)0.4.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
25
You have three cards, labeled 1, 2, and 3. You select two of the cards at random and note the numbers on the two cards. Let X be the sum of the two numbers labeled on the selected cards. Which of the following is the correct set of probabilities for X?
A)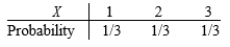
B)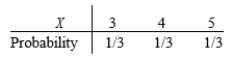
C)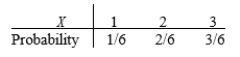
D)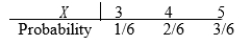
A)
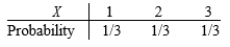
B)

C)
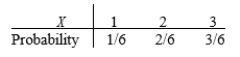
D)
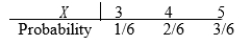

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
26
Horses are housed in pastures, pipe pens, or barn stalls at a local horse barn. Let X = the number of horses housed in barn stalls. Then X is:
A)a discrete random variable.
B)a continuous random variable.
C)an event.
D)the sample space.
A)a discrete random variable.
B)a continuous random variable.
C)an event.
D)the sample space.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
27
The density curve for a continuous random variable X has which of the following properties?
A)The probability of any event is the area under the density curve and above the values of X that make up the event.
B)The total area under the density curve for X must be exactly 1.
C)The probability of any event of the form X = constant is 0.
D)All of the answer options are correct.
A)The probability of any event is the area under the density curve and above the values of X that make up the event.
B)The total area under the density curve for X must be exactly 1.
C)The probability of any event of the form X = constant is 0.
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
28
At a small college, all entering freshmen must take a foreign language class, chosen from the languages Spanish, French, Swahili, Chinese, and Arabic. Because there is limited space in the foreign language courses, a student cannot simultaneously enroll in more than one course. The probability distribution for the language studied by a randomly selected freshman is summarized in the following table.  The probability that the freshman is studying Spanish is:
The probability that the freshman is studying Spanish is:
A)0.08.
B)0.52.
C)0.48.
D)The answer cannot be determined from the information given.
 The probability that the freshman is studying Spanish is:
The probability that the freshman is studying Spanish is:A)0.08.
B)0.52.
C)0.48.
D)The answer cannot be determined from the information given.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose we roll two fair four-sided dice. Let X denote the sum of the two roll outcomes. For example, if the first roll yields 3 and the second roll yields 1, then X = 3 + 1 = 4. The probability distribution for X is given below. 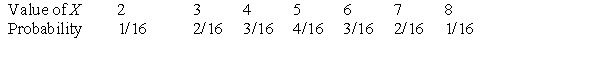 The probability of rolling a pair of 4s is:
The probability of rolling a pair of 4s is:
A)1/16.
B)1/8.
C)3/16.
D)13/16.
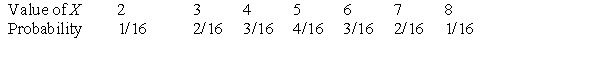 The probability of rolling a pair of 4s is:
The probability of rolling a pair of 4s is:A)1/16.
B)1/8.
C)3/16.
D)13/16.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
30
According to the Current Population Survey, the following table summarizes probabilities for randomly selecting a full-time student in various age groups: 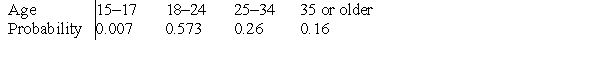 If we randomly select a full-time student, the probability that the student is 20-34 years old is:
If we randomly select a full-time student, the probability that the student is 20-34 years old is:
A)0.5.
B)0.703.
C)0.833.
D)The answer cannot be determined from the information provided.
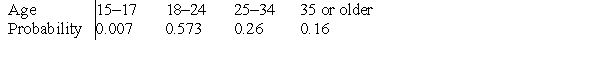 If we randomly select a full-time student, the probability that the student is 20-34 years old is:
If we randomly select a full-time student, the probability that the student is 20-34 years old is:A)0.5.
B)0.703.
C)0.833.
D)The answer cannot be determined from the information provided.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
31
A random variable can be described as:
A)a probability of an event.
B)a variable whose value is a numerical outcome of a random phenomenon.
C)the proportion of times an event occurs over a long run of repeated trials.
D)All of the answer options are correct.
A)a probability of an event.
B)a variable whose value is a numerical outcome of a random phenomenon.
C)the proportion of times an event occurs over a long run of repeated trials.
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
32
The amount of milk sold each day by a grocery store varies according to the Normal distribution with mean 130 gallons and standard deviation 12 gallons. On a randomly selected day, the probability that the store sells at least 154 gallons is:
A)0.0228.
B)0.1587.
C)0.8413.
D)0.9772.
A)0.0228.
B)0.1587.
C)0.8413.
D)0.9772.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
33
A basketball player makes 70% of her free throws. When fouled, she gets to take two free throws. Let X represent the number of free throws made in two tries. The probability distribution for the number of free throws she makes in two attempts is summarized in the following table.  The probability that she makes at least one free throw is:
The probability that she makes at least one free throw is:
A)0.67.
B)0.91.
C)0.95.
D)1.
 The probability that she makes at least one free throw is:
The probability that she makes at least one free throw is:A)0.67.
B)0.91.
C)0.95.
D)1.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
34
A sample of horses admitted to a local veterinary hospital had the following distribution of mares, geldings, and stallions.  If we assume that the horses constitute a random sample of all horses in the state, then we estimate the probability that a randomly selected horse is a stallion to be:
If we assume that the horses constitute a random sample of all horses in the state, then we estimate the probability that a randomly selected horse is a stallion to be:
A)5.11.
B)0.511.
C)0.0511.
D)None of the answer options is correct.
 If we assume that the horses constitute a random sample of all horses in the state, then we estimate the probability that a randomly selected horse is a stallion to be:
If we assume that the horses constitute a random sample of all horses in the state, then we estimate the probability that a randomly selected horse is a stallion to be:A)5.11.
B)0.511.
C)0.0511.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
35
The probability density of a random variable X is given in the following figure. 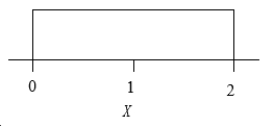 From this density, the probability that X is between 0.5 and 1.5 is:
From this density, the probability that X is between 0.5 and 1.5 is:
A)1/3.
B)1/2.
C)3/4.
D)1.
 From this density, the probability that X is between 0.5 and 1.5 is:
From this density, the probability that X is between 0.5 and 1.5 is:A)1/3.
B)1/2.
C)3/4.
D)1.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
36
A random sample of horses admitted to a local veterinary hospital found the following distribution of mares, geldings, and stallions. 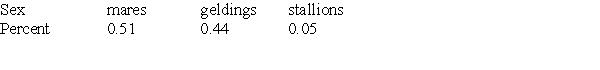 The probability that a horse newly arriving at the veterinary hospital is a male (gelding or stallion) is:
The probability that a horse newly arriving at the veterinary hospital is a male (gelding or stallion) is:
A)0.44.
B)0.05.
C)0.51.
D)0.49.
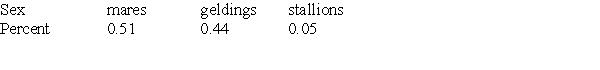 The probability that a horse newly arriving at the veterinary hospital is a male (gelding or stallion) is:
The probability that a horse newly arriving at the veterinary hospital is a male (gelding or stallion) is:A)0.44.
B)0.05.
C)0.51.
D)0.49.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
37
I choose a card at random from a well-shuffled deck of 52 cards. There is a 1/4 probability that the card chosen is a spade, a 1/4 probability that the card is a heart, a 1/4 probability that the card is a diamond, and a 1/4 probability that the card is a club. Both spades and clubs are black cards, whereas hearts and diamonds are red. The probability that the card chosen is not a spade is:
A)0.25.
B)0.5.
C)0.75.
D)1.
A)0.25.
B)0.5.
C)0.75.
D)1.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
38
According to the Current Population Survey, the following table summarizes probabilities for randomly selecting a full-time student in various age groups: 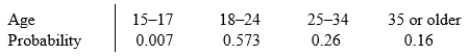 If we randomly select a full-time student, the probability that the student is not 18-24 years old is:
If we randomly select a full-time student, the probability that the student is not 18-24 years old is:
A)0.377.
B)0.427.
C)0.573.
D)0.993.
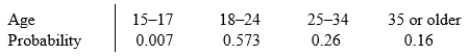 If we randomly select a full-time student, the probability that the student is not 18-24 years old is:
If we randomly select a full-time student, the probability that the student is not 18-24 years old is:A)0.377.
B)0.427.
C)0.573.
D)0.993.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
39
At a small college, all entering freshmen must take a foreign language class, chosen from the languages Spanish, French, Swahili, Chinese, and Arabic. Because there is limited space in the foreign language courses, a student cannot simultaneously enroll in more than one course. The probability distribution for the language studied by a randomly selected freshman is summarized in the following table. 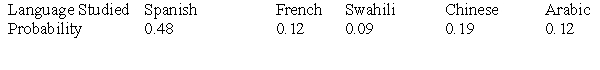 The probability that the freshman is studying Chinese or Swahili is:
The probability that the freshman is studying Chinese or Swahili is:
A)0.28.
B)0.31.
C)0.72.
D)1.
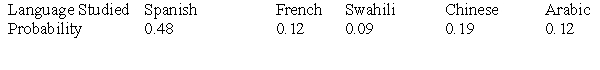 The probability that the freshman is studying Chinese or Swahili is:
The probability that the freshman is studying Chinese or Swahili is:A)0.28.
B)0.31.
C)0.72.
D)1.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
40
I choose a card at random from a well-shuffled deck of 52 cards. There is a 1/4 probability that the card chosen is a spade, a 1/4 probability that the card is a heart, a 1/4 probability that the card is a diamond, and a 1/4 probability that the card is a club. Both spades and clubs are black cards, whereas hearts and diamonds are red. The events card is a heart and card is a club are:
A)disjoint events.
B)impossible events.
C)independent events.
D)None of the answer options is correct.
A)disjoint events.
B)impossible events.
C)independent events.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
41
According to the M&Ms Web site, each package of the milk chocolate candies typically contains 14% brown, 13% red, 14% yellow, 16% green, 24% blue, and 20% orange M&Ms. You go to the store and buy a standard package. When you open it, you find that it contains 51 M&Ms, distributed as follows. 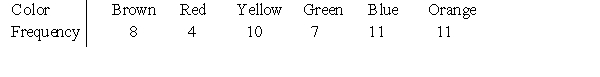 The variable color is:
The variable color is:
A)discrete.
B)continuous.
C)quantitative.
D)None of the answer options is correct.
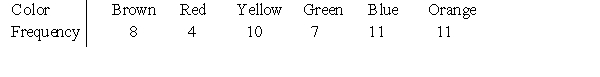 The variable color is:
The variable color is:A)discrete.
B)continuous.
C)quantitative.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
42
A geneticist developed a new type of pest-resistant walnut tree. These walnut trees produce 75% of pest-resistant walnut trees and 25% of susceptible (not resistant) trees when two resistant trees are crossed. If a grower crossed 100 such pairs of trees for 100 offspring, she will get:
A)exactly 70 resistant trees.
B)somewhere between 67 and 73 resistant trees.
C)somewhere between 64 and 73 resistant trees.
D)The answer cannot be determined.
A)exactly 70 resistant trees.
B)somewhere between 67 and 73 resistant trees.
C)somewhere between 64 and 73 resistant trees.
D)The answer cannot be determined.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
43
A geneticist developed a new type of pest-resistant walnut tree. These walnut trees produce 75% of pest-resistant walnut trees and 25% of susceptible (not resistant) trees when two resistant trees are crossed. If two such trees are crossed, we will get:
A)a resistant tree every third crossing.
B)a resistant tree for the first 70% of crossings and then susceptible trees.
C)approximately 70% of resistant trees over many crossings.
D)exactly 30% of susceptible trees over many crossings.
A)a resistant tree every third crossing.
B)a resistant tree for the first 70% of crossings and then susceptible trees.
C)approximately 70% of resistant trees over many crossings.
D)exactly 30% of susceptible trees over many crossings.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
44
A geneticist is conducting research on pest-resistant walnut trees. He has developed a set of trees, when crossed, to produce offspring as follows: 40% of all trees are very resistant, 30% of trees are somewhat resistant, and 20% are susceptible to invasion by pest, for the rest susceptibility status is unknown. Which of the following is a valid probability for an experiment of crossing two trees from his set?
A)P(susceptible)= 0.4, P(somewhat resistant)= 0.3, P(susceptible)= 0.2
B)P(susceptible)= 0.5, P(somewhat resistant)= 0.3, P(susceptible)= 0.2
C)P(susceptible)= 0.4, P(somewhat resistant)= 0.3, P(susceptible)= 0.3
D)None of the answer options is correct.
A)P(susceptible)= 0.4, P(somewhat resistant)= 0.3, P(susceptible)= 0.2
B)P(susceptible)= 0.5, P(somewhat resistant)= 0.3, P(susceptible)= 0.2
C)P(susceptible)= 0.4, P(somewhat resistant)= 0.3, P(susceptible)= 0.3
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
45
Every year, the veterinary hospital at a major research university treats a number of horses that have stones called enteroliths in their guts. A sample of 20 years shows that on average about 2% of horses presenting at the veterinary hospital are treated for enteroliths. Some breeds of horses seem more prone to developing enteroliths than others. Below is a table with the distribution of enteroliths among the breeds. 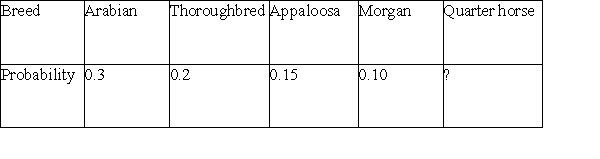 The probability that a horse arriving at the veterinary hospital is not an Arabian or a quarter horse is:
The probability that a horse arriving at the veterinary hospital is not an Arabian or a quarter horse is:
A)0.55.
B)0.25.
C)0.45.
D)0.75.
 The probability that a horse arriving at the veterinary hospital is not an Arabian or a quarter horse is:
The probability that a horse arriving at the veterinary hospital is not an Arabian or a quarter horse is:A)0.55.
B)0.25.
C)0.45.
D)0.75.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
46
According to the M&Ms Web site, each package of the milk chocolate candies typically contains 14% brown, 13% red, 14% yellow, 16% green, 24% blue, and 20% orange M&Ms. You go to the store and buy a standard package. When you open it, you find that it contains 51 M&Ms, distributed as follows. 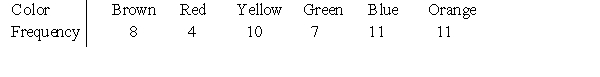 Over the long run, you know that the probability of selecting a blue or an orange M&M will be 44%, because these outcomes are:
Over the long run, you know that the probability of selecting a blue or an orange M&M will be 44%, because these outcomes are:
A)discrete.
B)disjoint.
C)finite.
D)None of the answer options is correct.
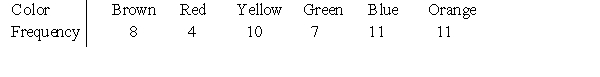 Over the long run, you know that the probability of selecting a blue or an orange M&M will be 44%, because these outcomes are:
Over the long run, you know that the probability of selecting a blue or an orange M&M will be 44%, because these outcomes are:A)discrete.
B)disjoint.
C)finite.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
47
A geneticist is conducting research on pest-resistant walnut trees. He has developed a set of trees, when crossed, to produce offspring as follows: 40% of all trees are very resistant, 30% of trees are somewhat resistant, and 20% are susceptible to invasion by pest, for the rest, susceptibility status is undetermined. The probability of a tree from a crossing being not resistant or an unknown status is:
A)P = 0.2.
B)P = 0.3.
C)P = 0.4.
D)P = 0.5.
A)P = 0.2.
B)P = 0.3.
C)P = 0.4.
D)P = 0.5.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
48
A geneticist is conducting research on pest-resistant walnut trees. He has developed a set of trees, when crossed, to produce offspring as follows: 50% of all trees are very resistant, 30% of trees are somewhat resistant, and 20% are susceptible to invasion by pest. The probability that a tree will be at least somewhat resistant is:
A)P = 0.3.
B)P = 0.5.
C)P = 0.8.
D)P = 0.7.
A)P = 0.3.
B)P = 0.5.
C)P = 0.8.
D)P = 0.7.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
49
Every year, the veterinary hospital at a major research university treats a number of horses that have stones called enteroliths in their guts. A sample of 20 years shows that, on average, about 2% of horses presenting at the veterinary hospital are treated for enteroliths. In the long run, the probability that a horse arriving at the veterinary hospital has enteroliths is:
A)0.05.
B)0.02.
C)0.5.
D)The answer cannot be determined from the information given.
A)0.05.
B)0.02.
C)0.5.
D)The answer cannot be determined from the information given.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
50
The high temperature X (in degrees Fahrenheit) on January days in Columbus, Ohio, varies according to the Normal distribution with mean 21 and standard deviation 10. The value of P(X < 10) is:
A)0.7433.
B)0.8643.
C)0.1357.
D)0.
A)0.7433.
B)0.8643.
C)0.1357.
D)0.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
51
An urn contains 3 red, 2 blue, and 5 green marbles. If we pick 4 marbles with replacement and count the number of red marbles in the 4 picks, the random variable is:
A)the number of red marbles.
B)the number of red, blue, or green marbles.
C)the number of green marbles.
D)None of the answer options is correct.
A)the number of red marbles.
B)the number of red, blue, or green marbles.
C)the number of green marbles.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
52
A geneticist developed a new type of pest-resistant walnuts. These walnuts produce 75% of pest-resistant walnut trees and 25% of susceptible (not resistant) trees when two resistant trees are crossed. If a grower crosses two such trees, the outcome is random and a probability model is given by outcomes:
A)resistant with probability 0.5 and susceptible with probability 0.5.
B)resistant with probability 0.75 and susceptible with probability 0.75.
C)resistant with probability 0.25 and susceptible with probability 0.25.
D)resistant with probability 0.75 and susceptible with probability 0.25.
A)resistant with probability 0.5 and susceptible with probability 0.5.
B)resistant with probability 0.75 and susceptible with probability 0.75.
C)resistant with probability 0.25 and susceptible with probability 0.25.
D)resistant with probability 0.75 and susceptible with probability 0.25.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
53
A geneticist is conducting research on pest-resistant walnut trees. He has developed a set of trees, when crossed, to produce offspring as follows: 50% of all trees are very resistant, 30% of trees are somewhat resistant, and 20% are susceptible to invasion by pest. The sample space consists of which of the following outcomes?
A)resistant, not resistant
B)very resistant, not very resistant
C)resistant, susceptible
D)very resistant, somewhat resistant, susceptible
A)resistant, not resistant
B)very resistant, not very resistant
C)resistant, susceptible
D)very resistant, somewhat resistant, susceptible

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
54
A geneticist is conducting research on pest-resistant walnut trees. He has developed a set of trees, when crossed, to produce offspring as follows: 40% of all trees are very resistant, 30% of trees are somewhat resistant, and 20% are susceptible to invasion by pest, for the rest, susceptibility status is undetermined. The probability of knowing that a tree from a crossing is at least somewhat resistant is:
A)P = 0.7.
B)P = 0.4.
C)P = 0.3.
D)P = 0.1.
A)P = 0.7.
B)P = 0.4.
C)P = 0.3.
D)P = 0.1.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
55
The high temperature X (in degrees Fahrenheit) on January days in Columbus, Ohio, varies according to the Normal distribution with mean 21 and standard deviation 10. If a January day in Columbus is randomly selected, what is the probability that the high temperature is between 15 and 25 degrees?
A)0.2743
B)0.6554
C)0.3811
D)almost 1
A)0.2743
B)0.6554
C)0.3811
D)almost 1

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
56
According to the M&Ms Web site, each package of the milk chocolate candies typically contains 14% brown, 13% red, 14% yellow, 16% green, 24% blue, and 20% orange M&Ms. You go to the store and buy a standard package. When you open it, you find that it contains 51 M&Ms, distributed as follows. 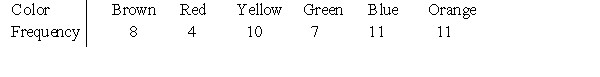 Choosing one M&M from your bag is an example of:
Choosing one M&M from your bag is an example of:
A)an event.
B)an outcome.
C)a set of outcomes.
D)None of the answer options is correct.
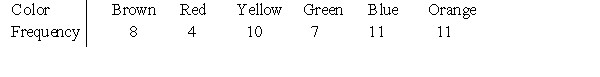 Choosing one M&M from your bag is an example of:
Choosing one M&M from your bag is an example of:A)an event.
B)an outcome.
C)a set of outcomes.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
57
A geneticist developed a new type of pest-resistant walnuts. These walnuts produce 75% of pest-resistant walnut trees and 25% of susceptible (not resistant) trees when two resistant trees are crossed. If a grower crossed 100 such pairs of trees for 100 offspring and did this many times over many years and plots, she should get:
A)approximately 70% of resistant trees over all plots and years.
B)exactly 70% of resistant trees over all plots and years.
C)exactly 70% of resistant trees in all plots and years.
D)None of the answer options is correct.
A)approximately 70% of resistant trees over all plots and years.
B)exactly 70% of resistant trees over all plots and years.
C)exactly 70% of resistant trees in all plots and years.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
58
A geneticist is conducting research on pest-resistant walnut trees. He has developed a set of trees, when crossed, to produce offspring as follows: 50% of all trees are very resistant, 30% of trees are somewhat resistant, and 20% are susceptible to invasion by pest. The probability model for the experiment of crossing two trees from the set of trees is:
A)P(susceptible)= 0.2, P(resistant)= 0.8.
B)P(very resistant)= 0.5, P(somewhat resistant)= 0.3, P(susceptible)=0.2.
C)P(very resistant)= 0.5, P(not very resistant)= 0.5.
D)P(susceptible)= 0.2, P(not susceptible)= 0.8.
A)P(susceptible)= 0.2, P(resistant)= 0.8.
B)P(very resistant)= 0.5, P(somewhat resistant)= 0.3, P(susceptible)=0.2.
C)P(very resistant)= 0.5, P(not very resistant)= 0.5.
D)P(susceptible)= 0.2, P(not susceptible)= 0.8.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
59
You have lived in Columbus for more than 20 years and know that there is at least a 75% chance of a high temperature above freezing on a particular January day. This is an example of:
A)the addition rule for disjoint events.
B)a sample space.
C)a personal probability.
D)a random variable.
A)the addition rule for disjoint events.
B)a sample space.
C)a personal probability.
D)a random variable.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
60
A geneticist developed a new type of pest-resistant walnuts. These walnuts produce 75% of pest-resistant walnut trees and 25% of susceptible (not resistant) trees when two resistant trees are crossed. If a grower crosses two such trees, the outcome is random and a probability model is given by:
A)resistant and susceptible.
B)probabilities p = 0.70 and p = 0.3.
C)P(resistant)= 0.75 and P(susceptible)= 0.25.
D)P(resistant)= 0.7.
A)resistant and susceptible.
B)probabilities p = 0.70 and p = 0.3.
C)P(resistant)= 0.75 and P(susceptible)= 0.25.
D)P(resistant)= 0.7.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
61
An urn contains 3 red, 2 blue, and 5 green marbles. If we pick 4 marbles with replacement and count the number of red marbles in the 4 picks, the probabilities associated with this experiment are P(0) = 0.24, P(1) = 0.41, P(2) = 0.265, P(3) = 0.076, and P(4) = 0.009. The probability of less than 2 red marbles is:
A)0.41.
B)0.65.
C)0.915.
D)0.991.
A)0.41.
B)0.65.
C)0.915.
D)0.991.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
62
An arborist is commissioned to study the amount of tree decay in a forest. The arborist obtains detailed information about the forest, the location, the annual rainfall, the type of tree species and other plants present, the pests and insects associated with tree death, and other information deemed relevant. On the basis of this information, the arborist reports that she puts the proportion of decayed trees at 22%. Therefore, she concludes that the probability of a randomly selected tree having decay is p = 0.22. This is an example of:
A)a frequency based probability.
B)a random probability.
C)a personal probability.
D)a fixed probability.
A)a frequency based probability.
B)a random probability.
C)a personal probability.
D)a fixed probability.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
63
An urn contains 3 red, 2 blue, and 5 green marbles. If we pick 4 marbles with replacement and count the number of red marbles in the 4 picks, the probabilities associated with this experiment are P(0) = 0.24, P(1) = 0.41, P(2) = 0.265, P(3) = 0.076, and P(4) = 0.009. The probability of 2 red marbles or less is:
A)0.41.
B)0.24.
C)0.65.
D)0.915.
A)0.41.
B)0.24.
C)0.65.
D)0.915.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
64
An urn contains 3 red, 2 blue, and 5 green marbles. If we pick 4 marbles with replacement and count the number of red marbles in the 4 picks, the probabilities associated with this experiment are P(0) = 0.24, P(1) = 0.41, P(2) = 0.265, P(3) = 0.076, and:
A)P(4)= 0.001.
B)P(4)= 0.005.
C)P(4)= 0.009.
D)The answer cannot be determined with information given.
A)P(4)= 0.001.
B)P(4)= 0.005.
C)P(4)= 0.009.
D)The answer cannot be determined with information given.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
65
An urn contains 3 red, 2 blue, and 5 green marbles. If we pick 4 marbles with replacement and count the number of red marbles in the 4 picks, the sample space is given by which of the following?
A)1, 2, 3, or 4 red marbles
B)4 marbles
C)red, green, blue
D)0, 1, 2, 3, or 4 marbles
A)1, 2, 3, or 4 red marbles
B)4 marbles
C)red, green, blue
D)0, 1, 2, 3, or 4 marbles

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
66
An urn contains 3 red, 2 blue, and 5 green marbles. If we pick 4 marbles with replacement and count the number of red marbles in the 4 picks, the probabilities associated with this experiment are P(0) = 0.24, P(1) = 0.41, P(2) = 0.265, P(3) = 0.076, and P(4) = 0.009. The probability of at least 1 red marble is:
A)0.24.
B)0.76.
C)0.009.
D)0.41.
A)0.24.
B)0.76.
C)0.009.
D)0.41.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck


