Deck 17: Line and Surface Integrals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 17: Line and Surface Integrals
1
Define 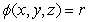 where
where 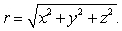 Compute the vector assigned to the point
Compute the vector assigned to the point 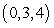 by the vector field
by the vector field 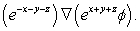
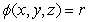 where
where 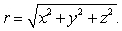 Compute the vector assigned to the point
Compute the vector assigned to the point 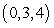 by the vector field
by the vector field 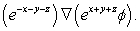
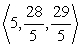
2
Let  be the curve
be the curve 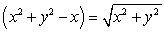 .
.
A) Parametrize using polar coordinates.
using polar coordinates.
B) Find the length of
 be the curve
be the curve  .
. A) Parametrize
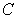 using polar coordinates.
using polar coordinates. B) Find the length of
A) 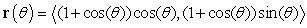 B) 8
B) 8
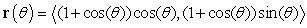 B) 8
B) 8 3
Define 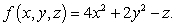 At what points is
At what points is 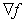 normal to the vector
normal to the vector 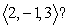
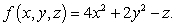 At what points is
At what points is 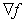 normal to the vector
normal to the vector 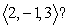
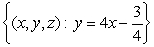
4
Let 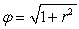 . Express
. Express 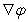 in terms of the unit radial vector
in terms of the unit radial vector 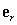 in
in 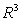 .
.
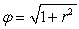 . Express
. Express 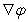 in terms of the unit radial vector
in terms of the unit radial vector 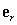 in
in 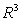 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
Compute the vector assigned to the point 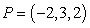 by the vector field
by the vector field 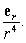
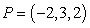 by the vector field
by the vector field 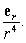

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
Let 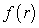 be a differentiable function of r, and let
be a differentiable function of r, and let 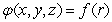 .
.
Express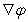 in terms of the unit radial vector
in terms of the unit radial vector 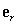 .
.
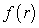 be a differentiable function of r, and let
be a differentiable function of r, and let 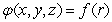 .
.Express
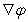 in terms of the unit radial vector
in terms of the unit radial vector 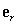 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
Find a potential function for the field 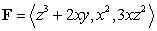 by inspection.
by inspection.
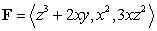 by inspection.
by inspection.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
Calculate the work performed by the force field 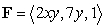 on a particle that moves in the counterclockwise direction around the quarter circle
on a particle that moves in the counterclockwise direction around the quarter circle 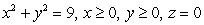 . Assume that
. Assume that 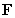 is in Newtons and the unit of distance is the meter.
is in Newtons and the unit of distance is the meter.
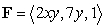 on a particle that moves in the counterclockwise direction around the quarter circle
on a particle that moves in the counterclockwise direction around the quarter circle 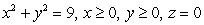 . Assume that
. Assume that  is in Newtons and the unit of distance is the meter.
is in Newtons and the unit of distance is the meter.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
Find a potential function for 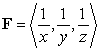 by inspection.
by inspection.
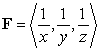 by inspection.
by inspection.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
Compute the work performed in moving a particle along the path 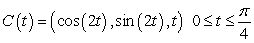 by the force
by the force 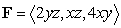 .
.
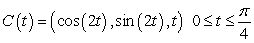 by the force
by the force 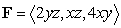 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
Define 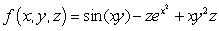 and
and 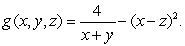 Compute
Compute 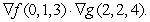
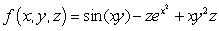 and
and 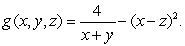 Compute
Compute 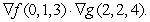

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
Define 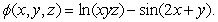 Compute the vector assigned to the point
Compute the vector assigned to the point 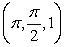 by the vector field
by the vector field 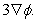
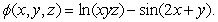 Compute the vector assigned to the point
Compute the vector assigned to the point 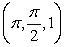 by the vector field
by the vector field 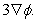

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
Compute 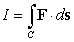 , where
, where 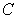 is the part of the ellipse
is the part of the ellipse 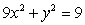 joining the point
joining the point 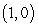 to the point
to the point 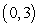 and
and 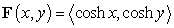 .
.
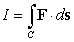 , where
, where 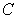 is the part of the ellipse
is the part of the ellipse 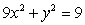 joining the point
joining the point 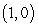 to the point
to the point 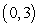 and
and 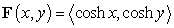 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
Let 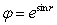 . Express
. Express 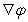 in terms of the unit radial vector
in terms of the unit radial vector 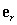 in
in 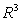 .
.
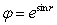 . Express
. Express 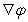 in terms of the unit radial vector
in terms of the unit radial vector 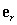 in
in 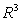 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
Let 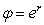 . Express
. Express 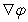 in terms of the unit radial vector
in terms of the unit radial vector 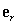 in
in 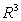 .
.
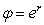 . Express
. Express 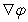 in terms of the unit radial vector
in terms of the unit radial vector 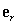 in
in 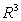 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
Let 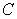 be the triangle with vertices at the points
be the triangle with vertices at the points 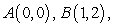 and
and 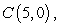 in counterclockwise order.
in counterclockwise order.
Compute the line integral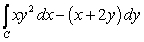 .
.
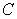 be the triangle with vertices at the points
be the triangle with vertices at the points 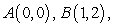 and
and 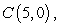 in counterclockwise order.
in counterclockwise order.Compute the line integral
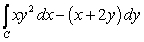 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
Determine whether the vector field 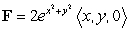 is a conservative vector field, and if so, find a potential function for
is a conservative vector field, and if so, find a potential function for 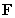 by inspection.
by inspection.
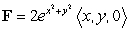 is a conservative vector field, and if so, find a potential function for
is a conservative vector field, and if so, find a potential function for 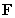 by inspection.
by inspection.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
Compute 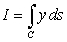 , where
, where 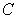 is the part of the parabola
is the part of the parabola 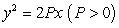 starting at
starting at 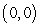 and ending at
and ending at 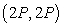 .
.
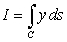 , where
, where 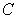 is the part of the parabola
is the part of the parabola 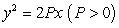 starting at
starting at 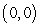 and ending at
and ending at 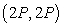 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
Let 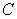 denote the closed curve of intersection of the hemisphere
denote the closed curve of intersection of the hemisphere 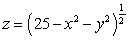 and the cylinder
and the cylinder 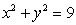 oriented counterclockwise.
oriented counterclockwise.
Compute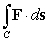 where
where 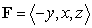 .
.
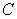 denote the closed curve of intersection of the hemisphere
denote the closed curve of intersection of the hemisphere 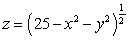 and the cylinder
and the cylinder 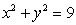 oriented counterclockwise.
oriented counterclockwise.Compute
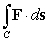 where
where 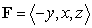 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate 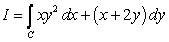 , where
, where  is the rectangle in
is the rectangle in  with vertices at
with vertices at  , and
, and 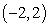 , in this order.
, in this order.
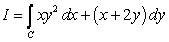 , where
, where 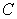 is the rectangle in
is the rectangle in 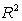 with vertices at
with vertices at 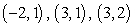 , and
, and 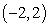 , in this order.
, in this order.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
Let 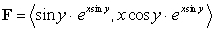 .
.
A) Determine whether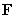 is conservative, and if so, find a potential function for
is conservative, and if so, find a potential function for 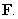
B) Compute the integral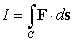 where C is the path
where C is the path 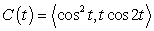 from
from 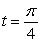 to
to 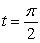 .
.
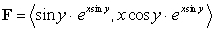 .
. A) Determine whether
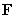 is conservative, and if so, find a potential function for
is conservative, and if so, find a potential function for 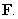
B) Compute the integral
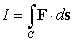 where C is the path
where C is the path 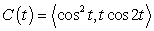 from
from 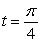 to
to 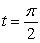 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
Let 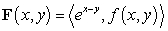 . Find a function
. Find a function  so that
so that  is conservative in
is conservative in  and
and 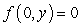 for all
for all 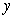 .
.
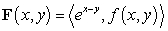 . Find a function
. Find a function 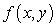 so that
so that 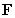 is conservative in
is conservative in 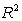 and
and 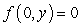 for all
for all 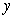 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
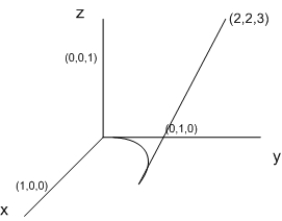
Evaluate 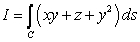 for the path C shown in the following figure. The path consists of the line segment from (1, 0, 0) to (0, 1, 0), followed by the circular arc in the yz-plane with radius 1 joining (0, 1, 0) to (0, 0, 1).
for the path C shown in the following figure. The path consists of the line segment from (1, 0, 0) to (0, 1, 0), followed by the circular arc in the yz-plane with radius 1 joining (0, 1, 0) to (0, 0, 1). 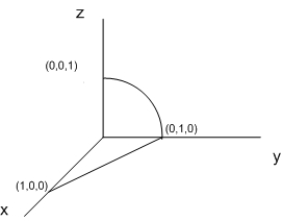
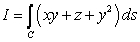 for the path C shown in the following figure. The path consists of the line segment from (1, 0, 0) to (0, 1, 0), followed by the circular arc in the yz-plane with radius 1 joining (0, 1, 0) to (0, 0, 1).
for the path C shown in the following figure. The path consists of the line segment from (1, 0, 0) to (0, 1, 0), followed by the circular arc in the yz-plane with radius 1 joining (0, 1, 0) to (0, 0, 1). 

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
Find  where
where 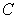 is the path
is the path 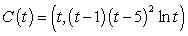 from
from 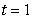 to
to 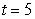 and
and 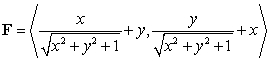 .
.
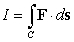 where
where 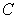 is the path
is the path  from
from 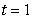 to
to 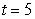 and
and 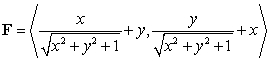 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
Compute the work performed in moving a particle along the path 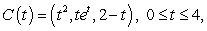 by the force
by the force 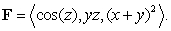
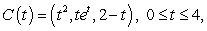 by the force
by the force 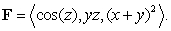

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
Compute the work performed in moving a particle along the path 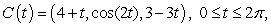 by the force
by the force 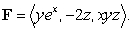
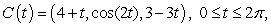 by the force
by the force 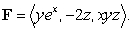

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
Compute the length of the parametric curve 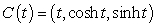 ,
, 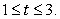
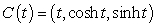 ,
, 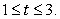

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
Compute the line integral 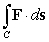 where C is the segment from
where C is the segment from 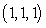 to
to 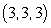 and
and 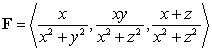 .
.
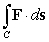 where C is the segment from
where C is the segment from 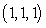 to
to 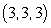 and
and 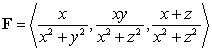 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
Let 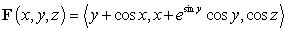 .
.
Determine whether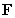 is conservative. If so, find a potential function.
is conservative. If so, find a potential function.
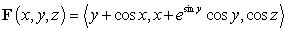 .
.Determine whether
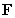 is conservative. If so, find a potential function.
is conservative. If so, find a potential function.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
Compute 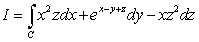 where C is the quarter circle on the
where C is the quarter circle on the 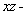 plane starting at
plane starting at 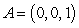 and ending at
and ending at 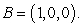
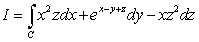 where C is the quarter circle on the
where C is the quarter circle on the 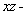 plane starting at
plane starting at 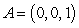 and ending at
and ending at 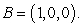

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate 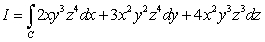 where C is the parametric curve
where C is the parametric curve 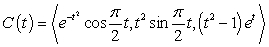 from
from 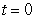 to
to 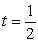 .
.
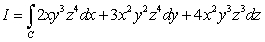 where C is the parametric curve
where C is the parametric curve 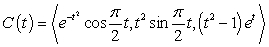 from
from 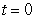 to
to 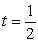 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
Compute the mass of the curve 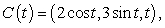
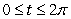 if the mass density is
if the mass density is 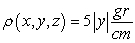 and
and 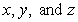 are measured in centimeters.
are measured in centimeters.
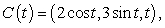
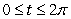 if the mass density is
if the mass density is 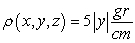 and
and 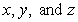 are measured in centimeters.
are measured in centimeters.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
Let 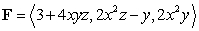 . Compute
. Compute 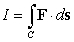 where
where  is the segment joining the points
is the segment joining the points  and
and  together with the quarter circle centered at the origin and joining the points
together with the quarter circle centered at the origin and joining the points 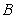 and
and 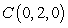 . The integration is performed from
. The integration is performed from 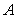 to
to 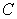 .
.
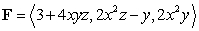 . Compute
. Compute 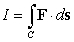 where
where 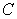 is the segment joining the points
is the segment joining the points 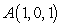 and
and 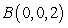 together with the quarter circle centered at the origin and joining the points
together with the quarter circle centered at the origin and joining the points 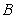 and
and 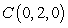 . The integration is performed from
. The integration is performed from 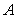 to
to 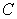 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
Let 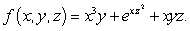
A) Compute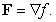
B) Evaluate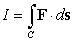 where C is the parametric curve
where C is the parametric curve 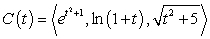 from
from 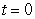 to
to 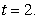
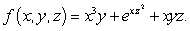
A) Compute
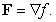
B) Evaluate
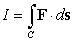 where C is the parametric curve
where C is the parametric curve 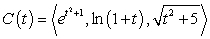 from
from 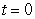 to
to 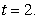

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
Let C be the curve 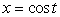 ,
, 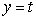 ,
, 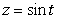 ,
, 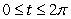 , and let
, and let 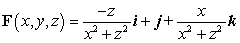 .
.
The value of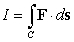 is which of the following?
is which of the following?
A)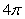
B)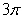
C)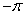
D)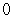
E) None of the answers is correct.
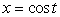 ,
, 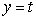 ,
, 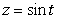 ,
, 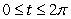 , and let
, and let 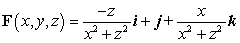 .
.The value of
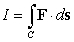 is which of the following?
is which of the following?A)
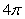
B)
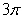
C)
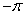
D)
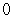
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
Compute the line integral 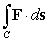 where C is the line segment from
where C is the line segment from 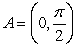 to
to 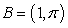 and
and 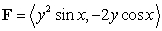 .
.
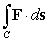 where C is the line segment from
where C is the line segment from 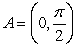 to
to 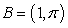 and
and 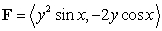 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
Compute the mass of the curve 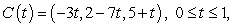 if the mass density is
if the mass density is 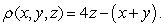
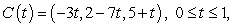 if the mass density is
if the mass density is 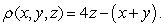

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
Compute 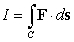 where
where 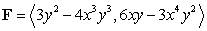 and
and 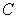 is the path
is the path 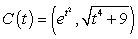 from
from 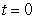 to
to 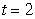 .
.
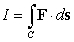 where
where 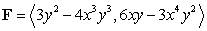 and
and 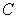 is the path
is the path 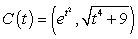 from
from 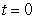 to
to 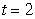 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate 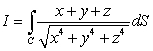 where C is the line segment joining the points
where C is the line segment joining the points 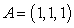 and
and 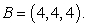
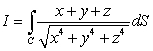 where C is the line segment joining the points
where C is the line segment joining the points 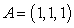 and
and 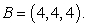

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
Compute the work performed in moving a particle along the path 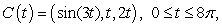 by the force
by the force 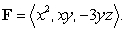
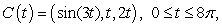 by the force
by the force 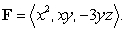

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
Find 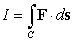 where
where 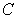 is the path
is the path 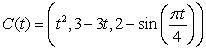 from
from 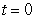 to
to 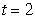 and
and 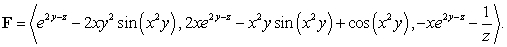
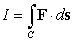 where
where 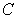 is the path
is the path 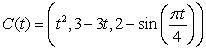 from
from 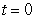 to
to 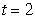 and
and 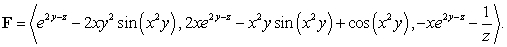

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
Let 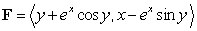 .
.
Compute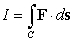 where C is the spiral
where C is the spiral 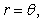
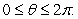
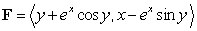 .
.Compute
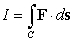 where C is the spiral
where C is the spiral 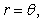

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
Let S denote the part of the surface 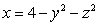 inside the cylinder
inside the cylinder 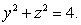 The area of S is closest to which of the following?
The area of S is closest to which of the following?
A)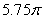
B)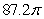
C)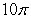
D)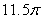
E)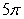
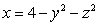 inside the cylinder
inside the cylinder 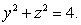 The area of S is closest to which of the following?
The area of S is closest to which of the following?A)
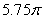
B)
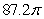
C)
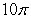
D)
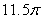
E)
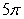

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
In the paraboloid 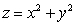 ,
, 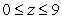 the charge density is equal to the distance from the
the charge density is equal to the distance from the 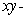 plane. Find the total charge in the paraboloid.
plane. Find the total charge in the paraboloid.
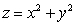 ,
, 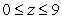 the charge density is equal to the distance from the
the charge density is equal to the distance from the 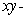 plane. Find the total charge in the paraboloid.
plane. Find the total charge in the paraboloid.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
Let 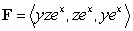 .
.
A) Determine whether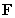 is conservative, and if so, find a potential function for
is conservative, and if so, find a potential function for 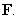
B) Compute the line integral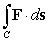 where C is the path consisting of:
where C is the path consisting of: 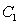 : the parabola
: the parabola 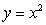 from
from 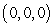 to
to 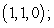
 : the line segment from
: the line segment from 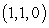 to
to 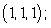 and
and  : the semicircle in the plane
: the semicircle in the plane 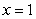 with diameter
with diameter 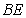 where
where 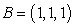 and
and 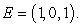
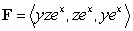 .
. A) Determine whether
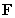 is conservative, and if so, find a potential function for
is conservative, and if so, find a potential function for 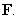
B) Compute the line integral
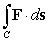 where C is the path consisting of:
where C is the path consisting of: 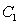 : the parabola
: the parabola 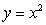 from
from 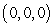 to
to 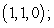
 : the line segment from
: the line segment from 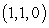 to
to 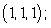 and
and 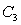 : the semicircle in the plane
: the semicircle in the plane 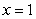 with diameter
with diameter 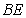 where
where 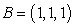 and
and 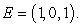

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
Compute 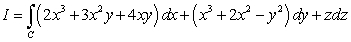 along the curve
along the curve 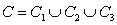 shown in the following figure.
shown in the following figure. 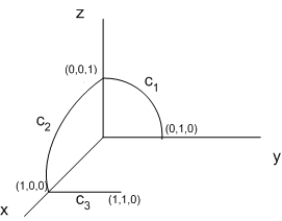
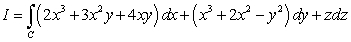 along the curve
along the curve 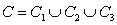 shown in the following figure.
shown in the following figure. 

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
Consider the vector field 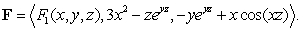 Find the formula for
Find the formula for  so that
so that  is conservative and
is conservative and 
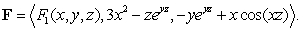 Find the formula for
Find the formula for 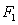 so that
so that 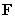 is conservative and
is conservative and 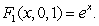

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the vector field 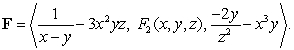 Find the formula for
Find the formula for 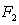 so that
so that 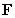 is conservative and
is conservative and 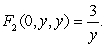
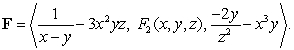 Find the formula for
Find the formula for 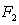 so that
so that 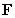 is conservative and
is conservative and 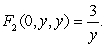

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
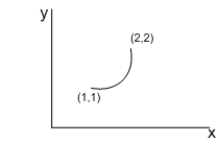
Let 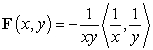 .
.
A) Does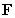 have a potential function? If so, find it.
have a potential function? If so, find it.
B) Find the integral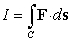 where C is the semicircle oriented counterclockwise with the diameter
where C is the semicircle oriented counterclockwise with the diameter 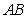 , where
, where 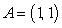 and
and 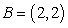 .
. 
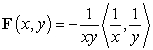 .
. A) Does
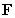 have a potential function? If so, find it.
have a potential function? If so, find it. B) Find the integral
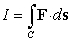 where C is the semicircle oriented counterclockwise with the diameter
where C is the semicircle oriented counterclockwise with the diameter 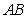 , where
, where 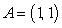 and
and 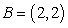 .
. 

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
Let 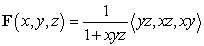 .
.
A) Determine whether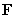 has a potential function, and if so, find a potential function for
has a potential function, and if so, find a potential function for 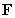 .
.
B) Compute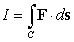 where
where 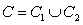 ,
, 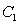 is the curve
is the curve 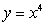 ,
, 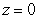 from
from 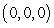 to
to 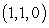 and
and 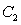 is the straight line from
is the straight line from 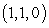 to
to 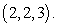
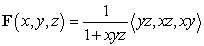 .
. A) Determine whether
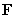 has a potential function, and if so, find a potential function for
has a potential function, and if so, find a potential function for 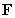 .
. B) Compute
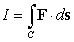 where
where 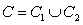 ,
, 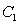 is the curve
is the curve 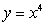 ,
, 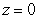 from
from 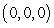 to
to 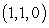 and
and 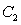 is the straight line from
is the straight line from 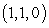 to
to 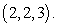


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
Compute 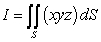 where S is the part of the plane
where S is the part of the plane 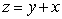 which lies inside the half cylinder
which lies inside the half cylinder 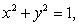
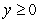 .
.
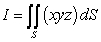 where S is the part of the plane
where S is the part of the plane 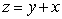 which lies inside the half cylinder
which lies inside the half cylinder 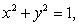
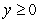 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
Find 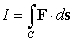 where
where 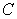 is the path
is the path 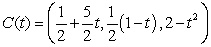 from
from 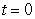 to
to 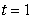 and
and 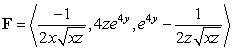 .
.
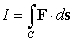 where
where 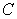 is the path
is the path 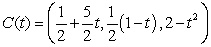 from
from 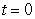 to
to 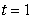 and
and 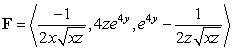 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
Find 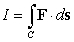 where
where 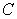 is the path
is the path 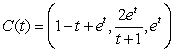 from
from 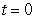 to
to 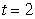 and
and 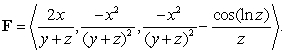
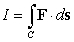 where
where 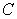 is the path
is the path 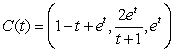 from
from 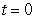 to
to 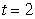 and
and 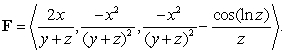

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
Consider the vector field 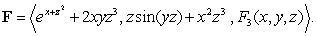 Find the formula for
Find the formula for 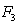 so that
so that 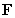 is conservative and
is conservative and 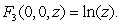
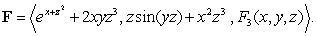 Find the formula for
Find the formula for 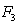 so that
so that 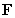 is conservative and
is conservative and 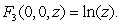

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
Compute the surface integral 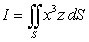 for the surface
for the surface 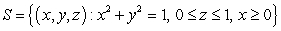 .
.
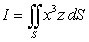 for the surface
for the surface 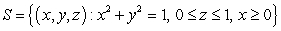 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
The surface integral 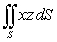 where
where 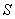 is the part of the plane
is the part of the plane 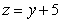 which lies inside the cylinder
which lies inside the cylinder 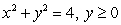 is which of the following?
is which of the following?
A)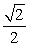
B)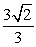
C)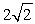
D) 0
E) None of the answers is correct.
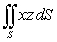 where
where 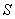 is the part of the plane
is the part of the plane 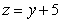 which lies inside the cylinder
which lies inside the cylinder 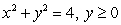 is which of the following?
is which of the following?A)
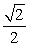
B)
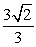
C)
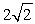
D) 0
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
The mass of the part of the cone 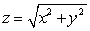 with
with 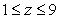 and density
and density 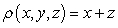 is which of the following?
is which of the following?
A)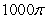
B)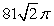
C)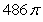
D)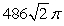
E) None of the answers is correct.
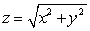 with
with 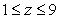 and density
and density 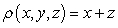 is which of the following?
is which of the following?A)
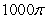
B)
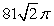
C)
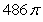
D)
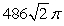
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
Find the surface area of the surface 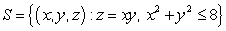 .
.
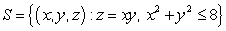 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the surface integral 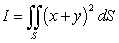 where S is the part of the cone
where S is the part of the cone 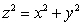 between the planes
between the planes 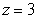 and
and 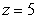 .
.
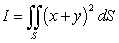 where S is the part of the cone
where S is the part of the cone 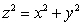 between the planes
between the planes 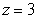 and
and 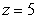 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
Find 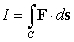 where
where 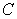 is the path
is the path 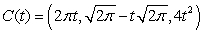 from
from 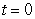 to
to 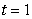 and
and 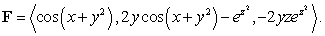
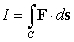 where
where 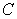 is the path
is the path 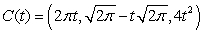 from
from 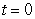 to
to 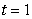 and
and 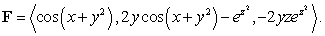

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
Let S be the surface 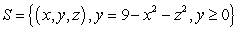 .
.
The area of S is approximately which of the following
A)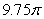
B)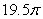
C)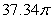
D)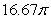
E) None of the answers is correct.
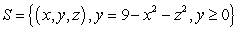 .
.The area of S is approximately which of the following
A)
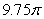
B)
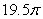
C)
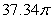
D)
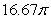
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
The integral 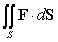 where
where 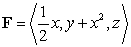 and
and 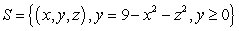 with normals pointing to the positive y direction is equal to which of the following?
with normals pointing to the positive y direction is equal to which of the following?
A)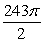
B)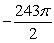
C)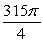
D)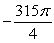
E)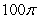
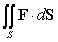 where
where 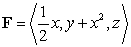 and
and 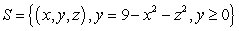 with normals pointing to the positive y direction is equal to which of the following?
with normals pointing to the positive y direction is equal to which of the following?A)
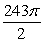
B)
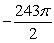
C)
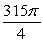
D)
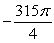
E)
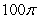

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
Compute 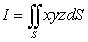 where S is the part of the plane
where S is the part of the plane 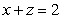 in the first octant bounded by the planes
in the first octant bounded by the planes 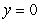 and
and 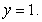
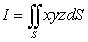 where S is the part of the plane
where S is the part of the plane 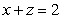 in the first octant bounded by the planes
in the first octant bounded by the planes 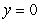 and
and 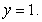

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate 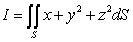 where
where 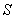 is the portion of the paraboloid
is the portion of the paraboloid 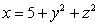 contained within the cylinder
contained within the cylinder 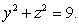
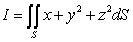 where
where 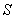 is the portion of the paraboloid
is the portion of the paraboloid 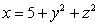 contained within the cylinder
contained within the cylinder 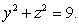

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
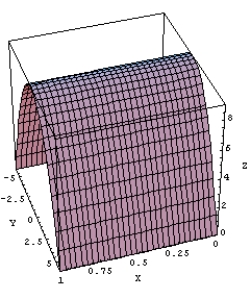
Evaluate 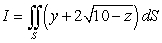 where S is the surface cut from the paraboloid
where S is the surface cut from the paraboloid 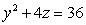 by the planes
by the planes 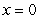 ,
, 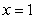 and
and 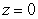 .
. 
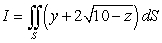 where S is the surface cut from the paraboloid
where S is the surface cut from the paraboloid 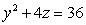 by the planes
by the planes 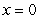 ,
, 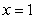 and
and 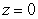 .
. 

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate 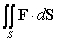 where
where 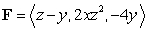 and
and 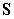 is the surface
is the surface 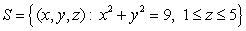 oriented outward.
oriented outward.
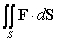 where
where 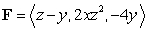 and
and 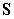 is the surface
is the surface 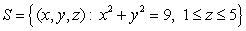 oriented outward.
oriented outward.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate 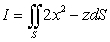 where
where 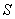 is the portion of the cylinder
is the portion of the cylinder 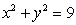 bounded between the planes
bounded between the planes 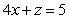 and
and 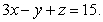
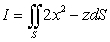 where
where 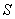 is the portion of the cylinder
is the portion of the cylinder 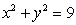 bounded between the planes
bounded between the planes 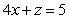 and
and 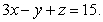

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
Find the flux of 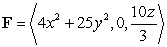 across the surface
across the surface 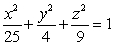 , oriented outward.
, oriented outward.
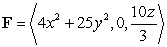 across the surface
across the surface 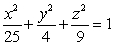 , oriented outward.
, oriented outward.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
Compute 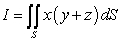 where S is the part of the surface
where S is the part of the surface 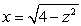 between the planes
between the planes 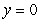 and
and 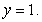
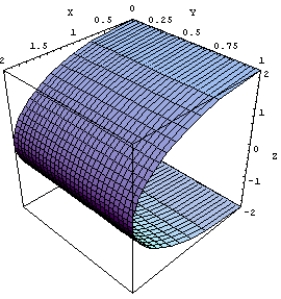
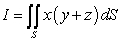 where S is the part of the surface
where S is the part of the surface 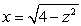 between the planes
between the planes 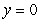 and
and 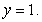


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
Compute the flux of water through the parabolic cylinder (oriented in the positive y-direction)
S :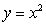 ,
, 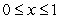 ,
, 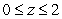 where the velocity vector is
where the velocity vector is 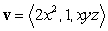 (in
(in 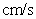 ).
).
S :
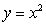 ,
, 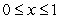 ,
, 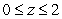 where the velocity vector is
where the velocity vector is 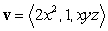 (in
(in 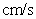 ).
).
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
Compute the area of the surface 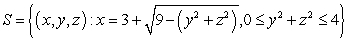 .
.
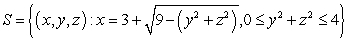 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
Find the surface area of the portion of the sphere 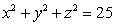 satisfying
satisfying 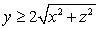
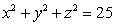 satisfying
satisfying 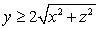

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
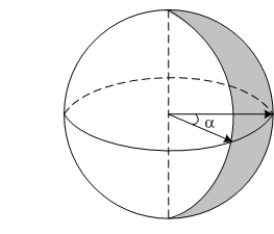
Let 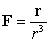 where
where 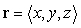 and
and 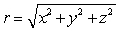 . Let
. Let 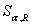 be a sector of angle
be a sector of angle 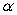 in the sphere of radius
in the sphere of radius 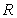 , centered at the origin and oriented outward. Find
, centered at the origin and oriented outward. Find 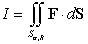 .
. 
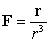 where
where 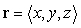 and
and 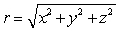 . Let
. Let 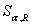 be a sector of angle
be a sector of angle 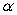 in the sphere of radius
in the sphere of radius 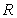 , centered at the origin and oriented outward. Find
, centered at the origin and oriented outward. Find 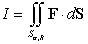 .
. 

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
The area of the surface 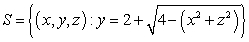 is which of the following?
is which of the following?
A)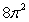
B)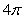
C)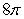
D)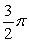
E) None of the answers is correct.
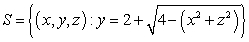 is which of the following?
is which of the following?A)
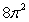
B)
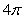
C)
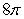
D)
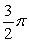
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
Find the flux of the field 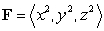 through the surface
through the surface 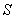 which is the part of the paraboloid
which is the part of the paraboloid 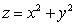 where
where 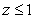 .
.
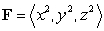 through the surface
through the surface 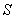 which is the part of the paraboloid
which is the part of the paraboloid 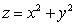 where
where 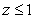 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
Compute the surface integral 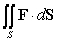 where
where 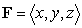 and
and 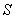 is the surface of the sphere centered at the origin with radius 4.
is the surface of the sphere centered at the origin with radius 4.
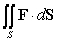 where
where 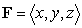 and
and 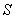 is the surface of the sphere centered at the origin with radius 4.
is the surface of the sphere centered at the origin with radius 4.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
Find the surface area of the portion of the cone 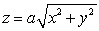 within the cylinder
within the cylinder 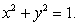
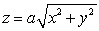 within the cylinder
within the cylinder 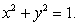

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
Find the flux 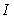 of the field
of the field 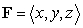 through the surface
through the surface 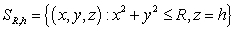 oriented upward.
oriented upward.
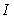 of the field
of the field 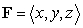 through the surface
through the surface 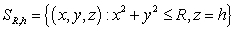 oriented upward.
oriented upward.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
Parametrize the surface 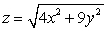 first using Cartesian coordinates and then using cylindrical coordinates. Assume x and y take on all real values.
first using Cartesian coordinates and then using cylindrical coordinates. Assume x and y take on all real values.
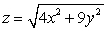 first using Cartesian coordinates and then using cylindrical coordinates. Assume x and y take on all real values.
first using Cartesian coordinates and then using cylindrical coordinates. Assume x and y take on all real values.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
Find the area of the ellipse cut from the plane 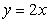 by the cylinder
by the cylinder 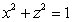 .
.
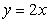 by the cylinder
by the cylinder 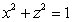 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


