Deck 15: Multiple Integrals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 15: Multiple Integrals
1
Evaluate the iterated integral by first changing the order of integration. 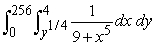
A)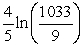
B)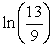
C)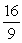
D)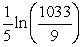
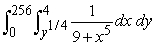
A)
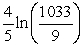
B)
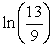
C)
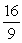
D)
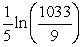
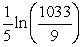
2
Evaluate the double integral. 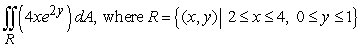
A)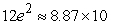
B)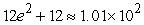
C)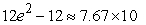
D)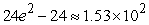
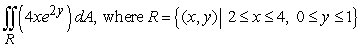
A)
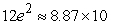
B)
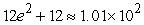
C)
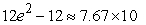
D)
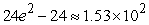
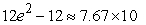
3
Find the volume of the solid bounded by the given surfaces. 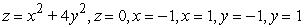
A)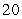
B)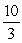
C) 40
D)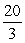
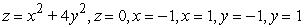
A)
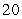
B)
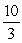
C) 40
D)
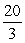
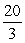
4
Approximate the double integral. 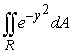 , where R is bounded by x = 0, x = 1, y = 0, and y = 2x + 3
, where R is bounded by x = 0, x = 1, y = 0, and y = 2x + 3
A) 1.772
B) 0.886
C) 2.658
D) 2.636
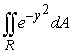 , where R is bounded by x = 0, x = 1, y = 0, and y = 2x + 3
, where R is bounded by x = 0, x = 1, y = 0, and y = 2x + 3A) 1.772
B) 0.886
C) 2.658
D) 2.636

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate the iterated integral by first changing the order of integration. 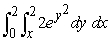
A)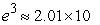
B)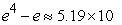
C)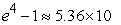
D)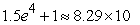
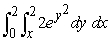
A)
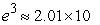
B)
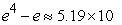
C)
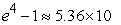
D)
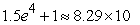

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
Compute the Riemann sum for the given function, the irregular partition shown and midpoint evaluation. 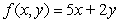
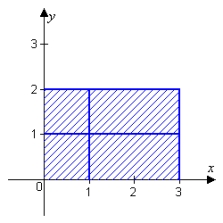
A) 48
B) 33
C) -57
D) 57
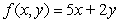

A) 48
B) 33
C) -57
D) 57

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate the iterated integral by first changing the order of integration. 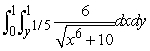
A)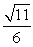
B)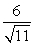
C)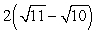
D) The integral can be evaluated only numerically.
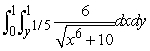
A)
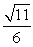
B)
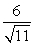
C)
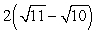
D) The integral can be evaluated only numerically.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
Compute the Riemann sum for the given function and region, a partition with n equal-sized rectangles and the given evaluation rule. 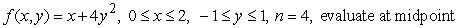
A) -8
B) 8
C) 0
D) -36
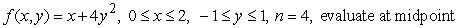
A) -8
B) 8
C) 0
D) -36

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
Find an integral equal to the volume of the solid bounded by the given surfaces and evaluate the integral. 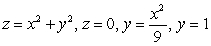
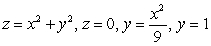

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
Change the order of integration. 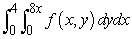
A)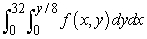
B)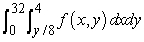
C)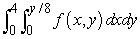
D)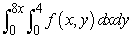
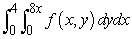
A)
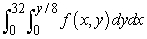
B)
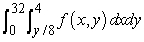
C)
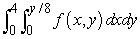
D)
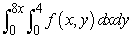

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate the iterated integral. 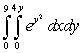
A)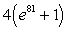
B)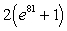
C)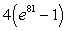
D)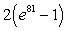
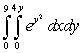
A)
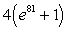
B)
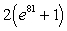
C)
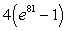
D)
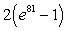

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
Compute the volume of the solid bounded by the given surfaces. 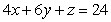 and the three coordinate planes
and the three coordinate planes
A)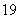
B)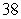
C)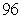
D)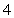
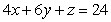 and the three coordinate planes
and the three coordinate planesA)
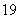
B)
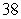
C)
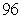
D)
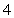

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
Change the order of integration. 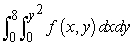
A)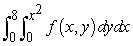
B)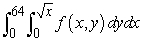
C)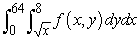
D)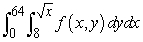
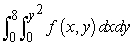
A)
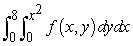
B)
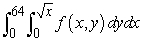
C)
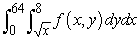
D)
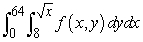

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate the iterated integral by first changing the order of integration. 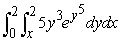
A)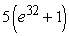
B)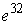
C)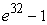
D) The integral can be evaluated only numerically.
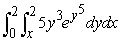
A)
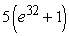
B)
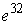
C)
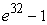
D) The integral can be evaluated only numerically.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
Use a double integral to find the area of the region bounded by 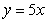 ,
, 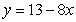 and
and 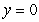 .
.
A)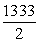
B)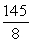
C)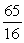
D)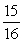
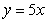 ,
, 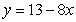 and
and 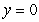 .
.A)
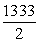
B)
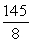
C)
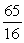
D)
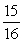

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the iterated integral. 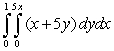
A)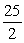
B)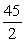
C)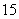
D)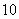
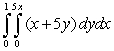
A)
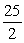
B)
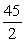
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
Find the volume of the solid bounded by the given surfaces. 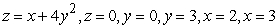
A)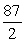
B)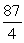
C) 117
D) 351
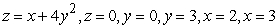
A)
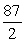
B)
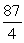
C) 117
D) 351

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
Use a double integral to find the area of the region bounded by 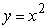 and
and 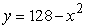 .
.
A)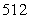
B)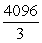
C)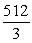
D)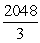
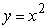 and
and 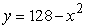 .
.A)
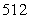
B)
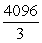
C)
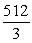
D)
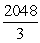

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the iterated integral. 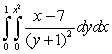
A)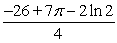
B)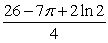
C)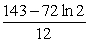
D)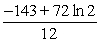
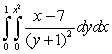
A)
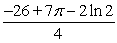
B)
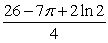
C)
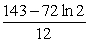
D)
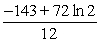

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the double integral. 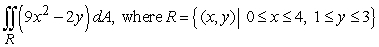
A) 352
B) 416
C) -352
D) -416
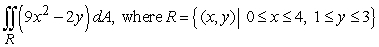
A) 352
B) 416
C) -352
D) -416

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
Find the surface area of the portion of 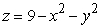 above the xy plane.
above the xy plane.
A)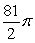
B)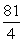
C)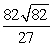
D)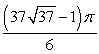
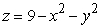 above the xy plane.
above the xy plane.A)
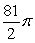
B)
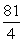
C)
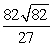
D)
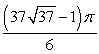

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
Find the surface area of 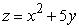 between
between 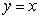 ,
, 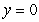 and
and 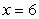 .
.
A)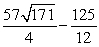
B)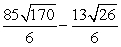
C)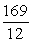
D)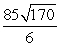
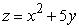 between
between 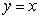 ,
, 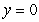 and
and 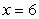 .
.A)
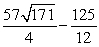
B)
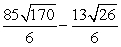
C)
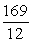
D)
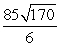

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate 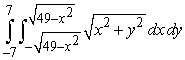 by converting to polar coordinates.
by converting to polar coordinates.
A)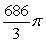
B)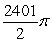
C)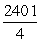
D)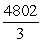
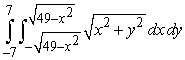 by converting to polar coordinates.
by converting to polar coordinates.A)
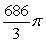
B)
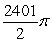
C)
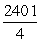
D)
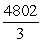

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
Suppose that 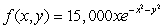 is the population density of a species of a certain small animal. Estimate the population in the triangular region
is the population density of a species of a certain small animal. Estimate the population in the triangular region 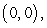
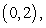 and
and 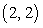 .
.
A) 4578
B) 1916
C) 4704
D) 1740
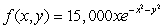 is the population density of a species of a certain small animal. Estimate the population in the triangular region
is the population density of a species of a certain small animal. Estimate the population in the triangular region 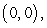
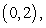 and
and 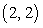 .
.A) 4578
B) 1916
C) 4704
D) 1740

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
Find the center of mass of a lamina in the shape of 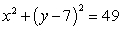 , with density
, with density 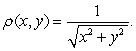
A)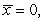
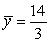
B)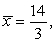
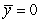
C)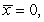
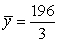
D)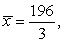
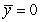
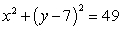 , with density
, with density 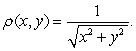
A)
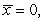
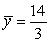
B)
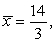
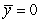
C)
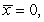
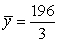
D)
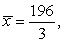
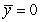

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
Find the surface area of the portion of 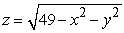 above
above 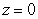 .
.
A)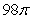
B)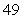
C)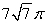
D)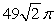
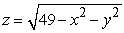 above
above 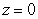 .
.A)
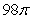
B)
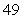
C)
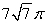
D)
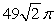

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
Find the surface area of the portion of the surface 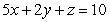 in the first octant.
in the first octant.
A)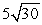
B)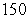
C)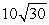
D)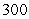
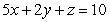 in the first octant.
in the first octant.A)
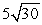
B)
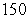
C)
D)
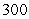

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate the iterated integral by converting to polar coordinates. 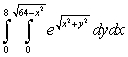
A)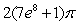
B)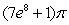
C)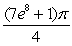
D)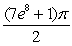
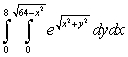
A)
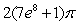
B)
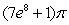
C)
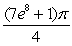
D)
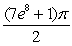

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
Find a constant c such that 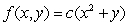 is a joint pdf on the region bounded by
is a joint pdf on the region bounded by 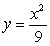 and
and 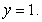
A)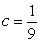
B)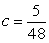
C)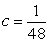
D)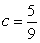
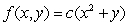 is a joint pdf on the region bounded by
is a joint pdf on the region bounded by 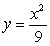 and
and 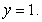
A)
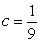
B)
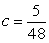
C)
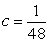
D)
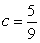

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
A skydiving club is having a competition to see who can land the closest to a target point. Jeff is a highly experienced skydiver, and the probability that he will land inside a region R is given by 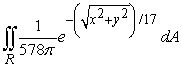 , where the coordinate system is centered on the target point. Compute the probability that Jeff lands within 11 feet of the target point.
, where the coordinate system is centered on the target point. Compute the probability that Jeff lands within 11 feet of the target point. 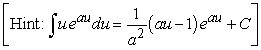
A)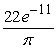
B)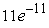
C)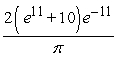
D)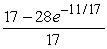
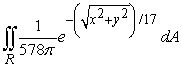 , where the coordinate system is centered on the target point. Compute the probability that Jeff lands within 11 feet of the target point.
, where the coordinate system is centered on the target point. Compute the probability that Jeff lands within 11 feet of the target point. 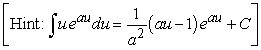
A)
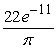
B)
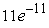
C)
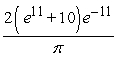
D)
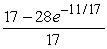

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
Use an appropriate coordinate system to compute the volume of the solid below 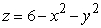 and above
and above 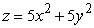 .
.
A)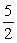
B)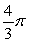
C)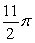
D)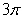
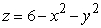 and above
and above 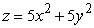 .
.A)
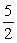
B)
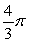
C)
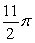
D)
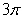

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
Find the area of the region bounded by 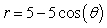
A)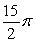
B)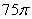
C)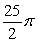
D)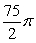
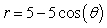
A)
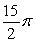
B)
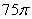
C)
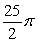
D)
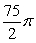

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
Use an appropriate coordinate system to compute the volume of the solid below 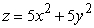 , above
, above 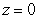 and inside
and inside 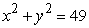 .
.
A)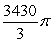
B)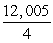
C)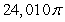
D)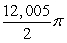
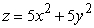 , above
, above 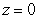 and inside
and inside 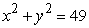 .
.A)
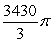
B)
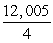
C)
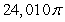
D)
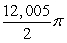

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
Use polar coordinates to evaluate 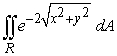 where R is the disk
where R is the disk 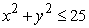 .
. 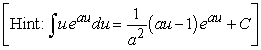
A)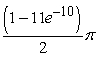
B)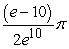
C)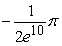
D)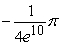
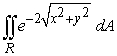 where R is the disk
where R is the disk 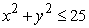 .
. 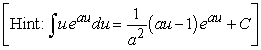
A)
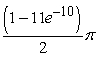
B)
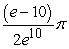
C)
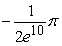
D)
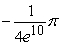

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
Use polar coordinates to evaluate 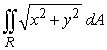 where R is the disk
where R is the disk 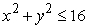 .
.
A)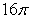
B)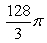
C)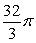
D)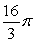
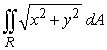 where R is the disk
where R is the disk 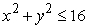 .
.A)
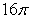
B)
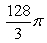
C)
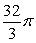
D)
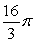

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
Find the mass and moments of inertia Ix and Iy for a lamina in the shape of the region bounded by 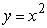 and
and 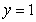 with density
with density 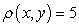 .
.
A)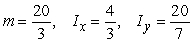
B)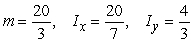
C)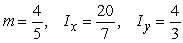
D)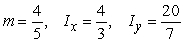
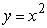 and
and 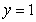 with density
with density 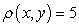 .
.A)
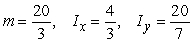
B)
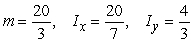
C)
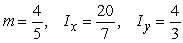
D)
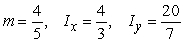

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
Compute the volume of the solid bounded by 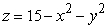 ,
, 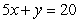 and the coordinate planes.
and the coordinate planes.
A)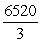
B)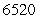
C)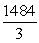
D)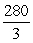
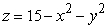 ,
, 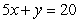 and the coordinate planes.
and the coordinate planes.A)
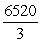
B)
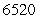
C)
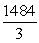
D)
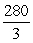

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
Find the surface area of the portion of 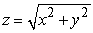 below
below 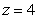 .
.
A)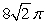
B)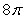
C)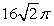
D)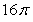
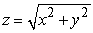 below
below 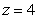 .
.A)
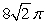
B)
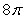
C)
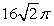
D)
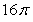

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
Compute the volume of the solid bounded by 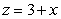 ,
, 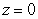 ,
, 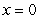 ,
, 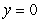 and
and 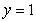 .
.
A)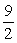
B)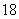
C)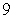
D)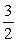
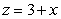 ,
, 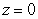 ,
, 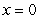 ,
, 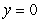 and
and 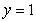 .
.A)
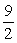
B)
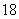
C)
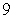
D)
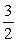

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
Find the mass and the center of mass of the lamina bounded by 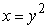 and
and 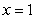 with density
with density 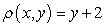 .
.
A)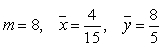
B)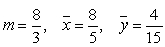
C)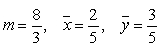
D)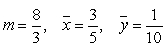
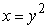 and
and 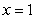 with density
with density 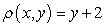 .
.A)
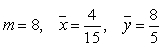
B)
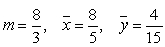
C)
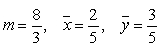
D)
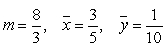

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate the triple integral 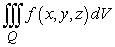 .
. 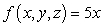 ,
, 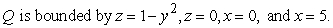
A)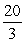
B)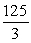
C)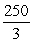
D)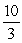
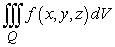 .
. 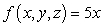 ,
, 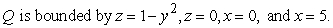
A)
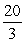
B)
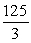
C)
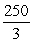
D)
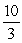

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
Find the center of mass of the solid with density 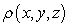 and the given shape.
and the given shape. 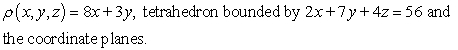
A)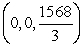
B)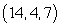
C)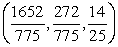
D)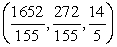
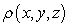 and the given shape.
and the given shape. 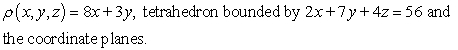
A)
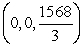
B)
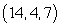
C)
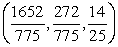
D)
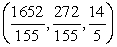

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
Find the mass of the solid with density 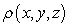 and the given shape.
and the given shape. 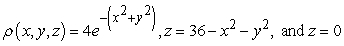 ,
,
A)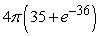
B)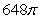
C)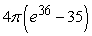
D)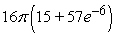
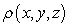 and the given shape.
and the given shape. 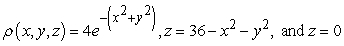 ,
,A)
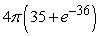
B)
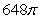
C)
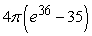
D)
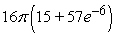

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
Find the mass of the solid with density 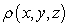 and the given shape.
and the given shape. 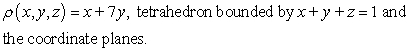
A)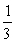
B)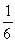
C)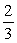
D)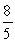
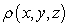 and the given shape.
and the given shape. 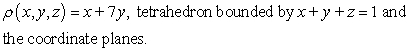
A)
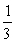
B)
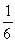
C)
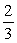
D)
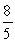

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
Find the center of mass of the solid with density 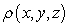 and the given shape.
and the given shape. 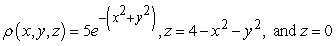 ,
,
A)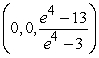
B)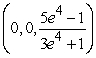
C)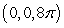
D)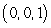
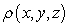 and the given shape.
and the given shape. 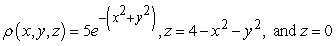 ,
,A)
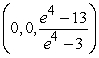
B)
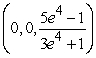
C)
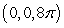
D)
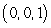

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
Compute the volume of the solid bounded by the given surfaces. 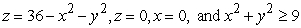
A)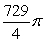
B)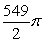
C)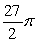
D)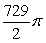
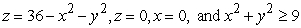
A)
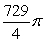
B)
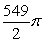
C)
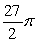
D)
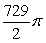

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
Write the equation 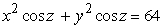 in cylindrical coordinates.
in cylindrical coordinates.
A)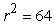
B)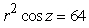
C)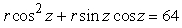
D)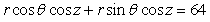
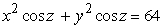 in cylindrical coordinates.
in cylindrical coordinates.A)
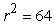
B)
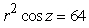
C)
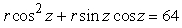
D)
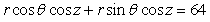

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
Numerically estimate the surface area of the portion of 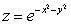 inside of
inside of 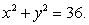
A) 3.14
B) 5.57
C) 116.24
D) 114.51
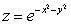 inside of
inside of 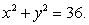
A) 3.14
B) 5.57
C) 116.24
D) 114.51

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate the triple integral. 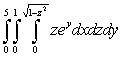
A)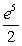
B)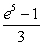
C)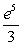
D)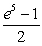
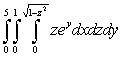
A)
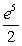
B)
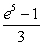
C)
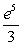
D)
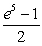

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
Write the equation 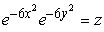 in cylindrical coordinates.
in cylindrical coordinates.
A)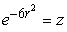
B)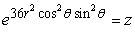
C)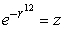
D)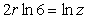
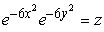 in cylindrical coordinates.
in cylindrical coordinates.A)
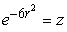
B)
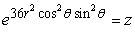
C)
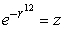
D)
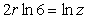

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the triple integral 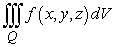 .
. 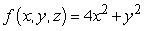 ,
, 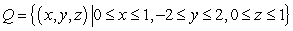
A) 4
B)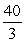
C) 0
D)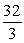
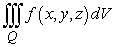 .
. 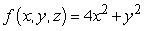 ,
, 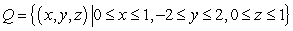
A) 4
B)
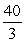
C) 0
D)
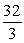

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
Compute the volume of the solid bounded by the given surfaces. 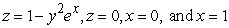
A)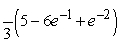
B)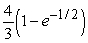
C)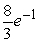
D)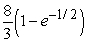
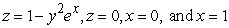
A)
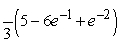
B)
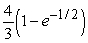
C)
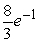
D)
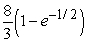

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the triple integral 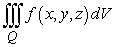 .
. 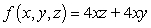 ,
, 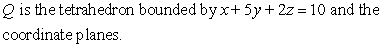
A)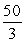
B) 10
C)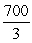
D)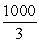
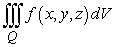 .
. 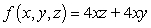 ,
, 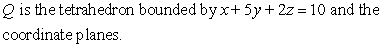
A)
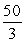
B) 10
C)
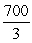
D)
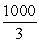

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the integral 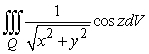 , where Q is the region with z > 0 bounded by
, where Q is the region with z > 0 bounded by 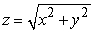 and
and 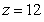 .
.
A)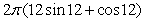
B)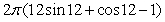
C)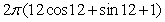
D)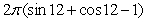
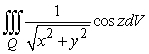 , where Q is the region with z > 0 bounded by
, where Q is the region with z > 0 bounded by 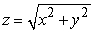 and
and 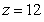 .
.A)
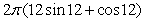
B)
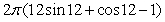
C)
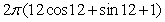
D)
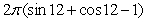

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
Evaluate the integral 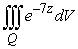 , where Q is the region with z > 0 bounded by
, where Q is the region with z > 0 bounded by 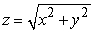 and
and 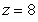 .
.
A)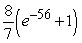
B)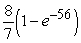
C)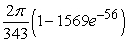
D)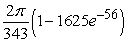
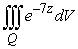 , where Q is the region with z > 0 bounded by
, where Q is the region with z > 0 bounded by 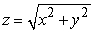 and
and 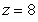 .
.A)
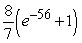
B)
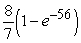
C)
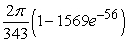
D)
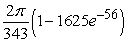

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
A function 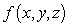 is a pdf on the three-dimensional region Q if
is a pdf on the three-dimensional region Q if 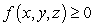 for all
for all 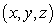 in Q and
in Q and 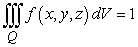 . Find k such that
. Find k such that 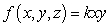 is a pdf on the region bounded by z = 0, z = 3, x = 0, x = 1, y - z = 0 , and y - z = 3.
is a pdf on the region bounded by z = 0, z = 3, x = 0, x = 1, y - z = 0 , and y - z = 3.
A)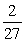
B)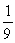
C)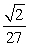
D)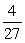
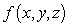 is a pdf on the three-dimensional region Q if
is a pdf on the three-dimensional region Q if 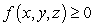 for all
for all 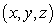 in Q and
in Q and 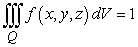 . Find k such that
. Find k such that 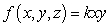 is a pdf on the region bounded by z = 0, z = 3, x = 0, x = 1, y - z = 0 , and y - z = 3.
is a pdf on the region bounded by z = 0, z = 3, x = 0, x = 1, y - z = 0 , and y - z = 3.A)
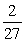
B)
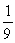
C)
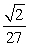
D)
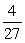

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
Set up the triple integral 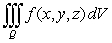 in cylindrical coordinates where Q is the solid above
in cylindrical coordinates where Q is the solid above 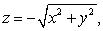 below
below 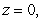 and inside
and inside 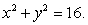
A)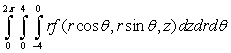
B)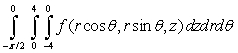
C)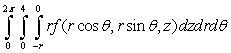
D)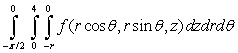
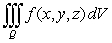 in cylindrical coordinates where Q is the solid above
in cylindrical coordinates where Q is the solid above 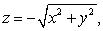 below
below 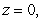 and inside
and inside 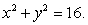
A)
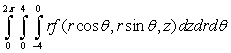
B)
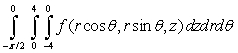
C)
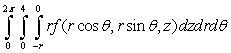
D)
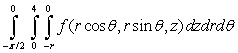

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
Rewrite the iterated integral by iterating in the order 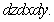
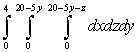
A)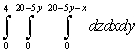
B)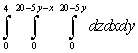
C)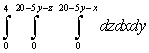
D)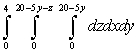
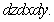
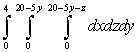
A)
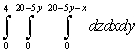
B)
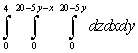
C)
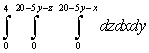
D)
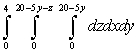

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
Which if the following could represent the triple integral 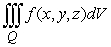 in cylindrical coordinates where Q is the region below
in cylindrical coordinates where Q is the region below 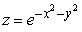 and above
and above 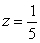 ?
?
A)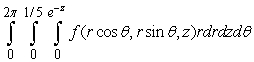
B)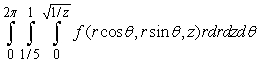
C)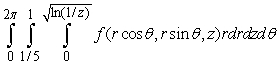
D)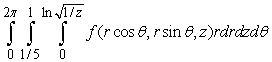
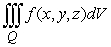 in cylindrical coordinates where Q is the region below
in cylindrical coordinates where Q is the region below 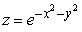 and above
and above 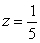 ?
?A)
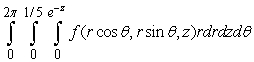
B)
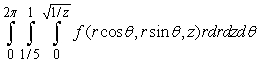
C)
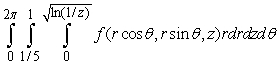
D)
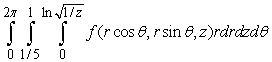

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
Which of the following could represent the triple integral 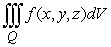 in cylindrical coordinates where Q is the region bounded below by
in cylindrical coordinates where Q is the region bounded below by 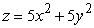 and above by
and above by 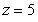 ?
?
A)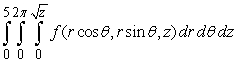
B)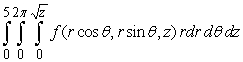
C)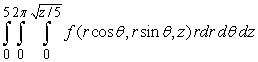
D)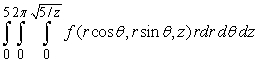
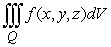 in cylindrical coordinates where Q is the region bounded below by
in cylindrical coordinates where Q is the region bounded below by 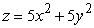 and above by
and above by 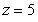 ?
?A)
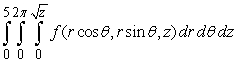
B)
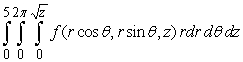
C)
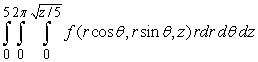
D)
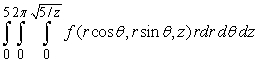

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
Convert the equation 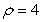 in spherical coordinates to an equation in rectangular coordinates.
in spherical coordinates to an equation in rectangular coordinates.
A)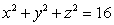
B)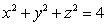
C)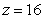
D)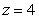
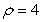 in spherical coordinates to an equation in rectangular coordinates.
in spherical coordinates to an equation in rectangular coordinates.A)
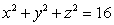
B)
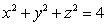
C)
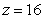
D)
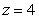

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate the iterated integral 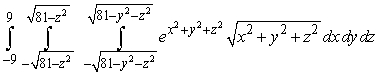 by changing coordinate systems.
by changing coordinate systems.
A)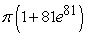
B)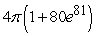
C)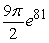
D)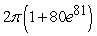
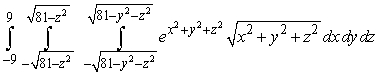 by changing coordinate systems.
by changing coordinate systems.A)
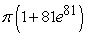
B)
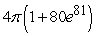
C)
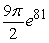
D)
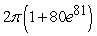

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
Use an appropriate coordinate system to find the volume of a solid lying outside the cones defined by 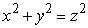 (includes the portion extending to z < 0) and inside the sphere defined by
(includes the portion extending to z < 0) and inside the sphere defined by 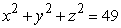 .
.
A)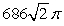
B)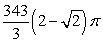
C)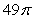
D)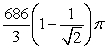
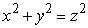 (includes the portion extending to z < 0) and inside the sphere defined by
(includes the portion extending to z < 0) and inside the sphere defined by 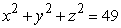 .
.A)
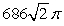
B)
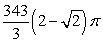
C)
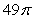
D)
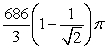

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
Use an appropriate coordinate system to find the volume of the solid lying along the positive z-axis and bounded by the cone 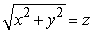 and the sphere
and the sphere 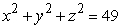 .
.
A)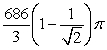
B)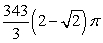
C)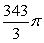
D)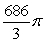
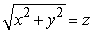 and the sphere
and the sphere 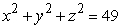 .
.A)
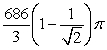
B)
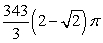
C)
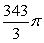
D)
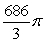

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate the iterated integral after changing coordinate systems. 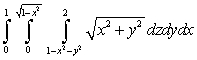
A)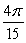
B)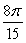
C)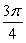
D)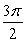
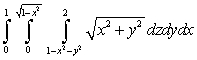
A)
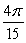
B)
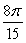
C)
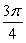
D)
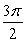

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
Calculate the mass of an object with density 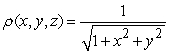 and bounded by
and bounded by 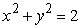 and the planes
and the planes 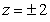 .
.
A)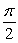
B)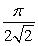
C)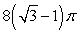
D)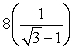
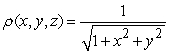 and bounded by
and bounded by 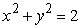 and the planes
and the planes 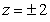 .
.A)
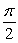
B)
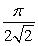
C)
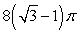
D)
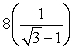

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
Compute the volume of the solid Q bounded by 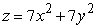 and
and 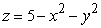 .
.
A)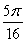
B)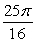
C)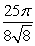
D)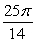
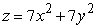 and
and 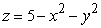 .
.A)
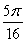
B)
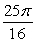
C)
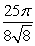
D)
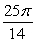

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
Using an appropriate coordinate system, evaluate the integral 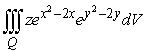 where Q is the region inside the cylinder
where Q is the region inside the cylinder 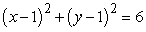 and between the planes
and between the planes 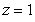 and
and 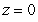 .
.
A)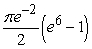
B)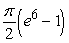
C)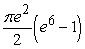
D)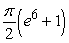
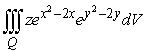 where Q is the region inside the cylinder
where Q is the region inside the cylinder 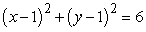 and between the planes
and between the planes 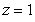 and
and 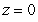 .
.A)
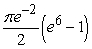
B)
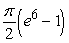
C)
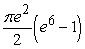
D)
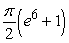

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
Evaluate the triple integral 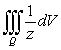 where Q is the bounded by
where Q is the bounded by 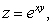
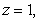
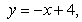
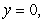 and
and 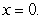
A)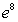
B)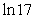
C)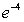
D)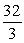
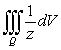 where Q is the bounded by
where Q is the bounded by 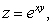
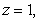
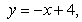
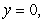 and
and 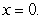
A)
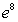
B)
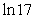
C)
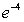
D)
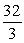

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
Set up and evaluate the integral 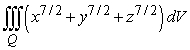 where Q is the region bounded by the coordinate planes and the planes x = 2, y = 2, and z = 2.
where Q is the region bounded by the coordinate planes and the planes x = 2, y = 2, and z = 2.
A)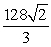
B)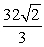
C)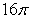
D)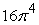
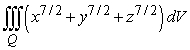 where Q is the region bounded by the coordinate planes and the planes x = 2, y = 2, and z = 2.
where Q is the region bounded by the coordinate planes and the planes x = 2, y = 2, and z = 2.A)
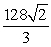
B)
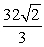
C)
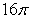
D)
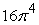

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
Convert the point 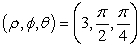 to rectangular coordinates (x,y,z).
to rectangular coordinates (x,y,z).
A)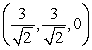
B)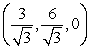
C)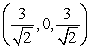
D)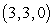
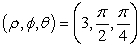 to rectangular coordinates (x,y,z).
to rectangular coordinates (x,y,z).A)
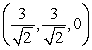
B)
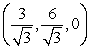
C)
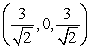
D)
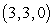

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
Convert the equation 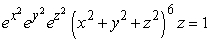 into spherical coordinates.
into spherical coordinates.
A)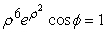
B)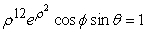
C)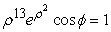
D)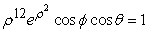
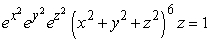 into spherical coordinates.
into spherical coordinates.A)
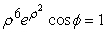
B)
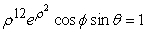
C)
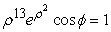
D)
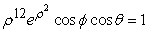

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate the iterated integral 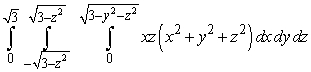 by changing coordinate systems.
by changing coordinate systems.
A)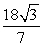
B)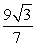
C)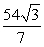
D)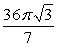
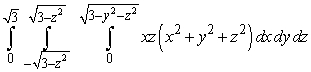 by changing coordinate systems.
by changing coordinate systems.A)
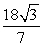
B)
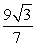
C)
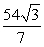
D)
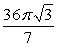

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
Set up and evaluate the integral 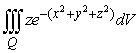 where Q is the region above the xy-plane bounded by the hemisphere centered at (0,0,0) and with a radius of 4.
where Q is the region above the xy-plane bounded by the hemisphere centered at (0,0,0) and with a radius of 4.
A)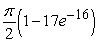
B)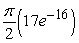
C) 0
D)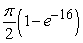
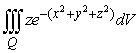 where Q is the region above the xy-plane bounded by the hemisphere centered at (0,0,0) and with a radius of 4.
where Q is the region above the xy-plane bounded by the hemisphere centered at (0,0,0) and with a radius of 4.A)
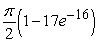
B)
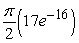
C) 0
D)
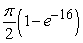

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
Set up and evaluate the integral 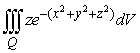 where Q is the region inside a sphere centered at (0,0,0) and with a radius of 5.
where Q is the region inside a sphere centered at (0,0,0) and with a radius of 5.
A)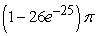
B) 0
C)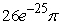
D)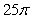
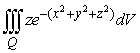 where Q is the region inside a sphere centered at (0,0,0) and with a radius of 5.
where Q is the region inside a sphere centered at (0,0,0) and with a radius of 5.A)
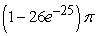
B) 0
C)
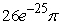
D)
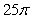

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the iterated integral after changing coordinate systems. 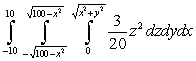
A)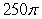
B)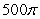
C)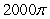
D)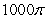
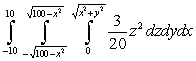
A)
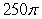
B)
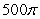
C)
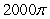
D)
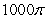

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
Using an appropriate coordinate system, evaluate the integral 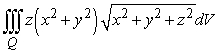 where Q is the region above z = 0 bounded by the cone
where Q is the region above z = 0 bounded by the cone 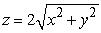 and the sphere
and the sphere 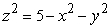 .
.
A)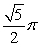
B)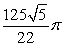
C)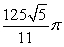
D)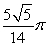
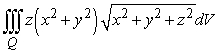 where Q is the region above z = 0 bounded by the cone
where Q is the region above z = 0 bounded by the cone 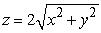 and the sphere
and the sphere 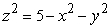 .
.A)
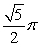
B)
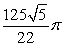
C)
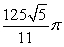
D)
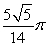

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
Convert the point 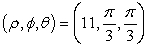 to rectangular coordinates (x,y,z).
to rectangular coordinates (x,y,z).
A)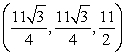
B)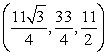
C)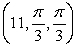
D)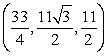
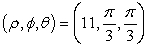 to rectangular coordinates (x,y,z).
to rectangular coordinates (x,y,z).A)
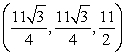
B)
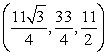
C)
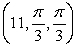
D)
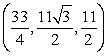

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
Calculate the mass of an object with density 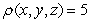 and bounded by
and bounded by 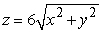 and
and 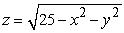
A)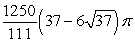
B)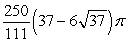
C)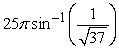
D)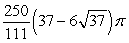
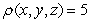 and bounded by
and bounded by 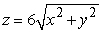 and
and 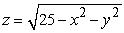
A)
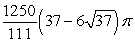
B)
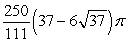
C)
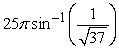
D)
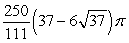

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
Using an appropriate coordinate system, evaluate the integral 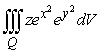 where Q is the region inside the cylinder
where Q is the region inside the cylinder 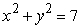 and between the planes
and between the planes 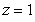 and
and 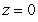 .
.
A)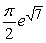
B)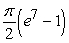
C)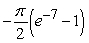
D)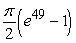
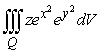 where Q is the region inside the cylinder
where Q is the region inside the cylinder 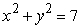 and between the planes
and between the planes 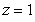 and
and 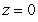 .
.A)
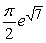
B)
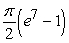
C)
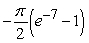
D)
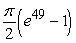

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


