Deck 16: Second Order Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/38
Play
Full screen (f)
Deck 16: Second Order Differential Equations
1
Identify the general solution of the the differential equation 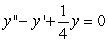 .
.
A)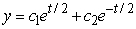
B)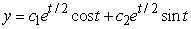
C)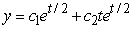
D)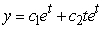
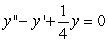 .
.A)
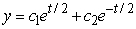
B)
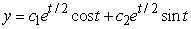
C)
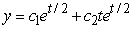
D)
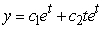
C
2
Solve the initial value problem 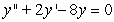 ,
, 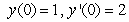 .
.
A)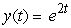
B)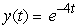
C)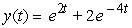
D)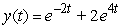
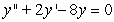 ,
, 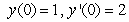 .
.A)
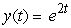
B)
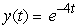
C)
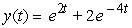
D)
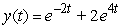
A
3
Identify the general solution of the the differential equation 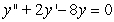 .
.
A)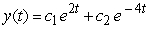
B)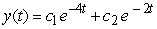
C)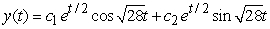
D)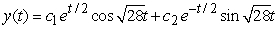
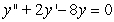 .
.A)
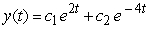
B)
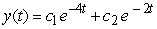
C)
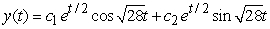
D)
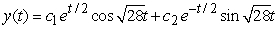
A
4
Solve the initial value problem. 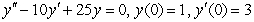
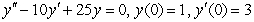

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
5
A 0.15 kg mass hangs on a spring with a 2 N m-1 force constant and its motion is damped proportional to its velocity with proportionality constant 0.2 kg s-1. If the system is subjected to an external variable-frequency vibration described as 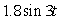 newtons, what will be the amplitude of the steady-state oscillation?
newtons, what will be the amplitude of the steady-state oscillation?
A) 2.03 m
B) 4.14 m
C) 0.12 m
D) 0.00 m
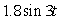 newtons, what will be the amplitude of the steady-state oscillation?
newtons, what will be the amplitude of the steady-state oscillation?A) 2.03 m
B) 4.14 m
C) 0.12 m
D) 0.00 m

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
6
Consider solutions to the second order differential equation 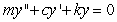 in which m, c, and k are positive constants. Which of the following pairs of graphs might correspond to the sets of constants m = 1.00, c = 0.80, and k = 1.20 (blue graph), and m = 1.00, c = 0.08, and k = 1.20 (red graph) ?
in which m, c, and k are positive constants. Which of the following pairs of graphs might correspond to the sets of constants m = 1.00, c = 0.80, and k = 1.20 (blue graph), and m = 1.00, c = 0.08, and k = 1.20 (red graph) ?
A)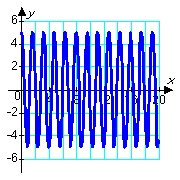
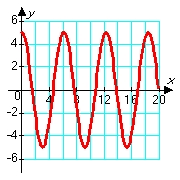
B)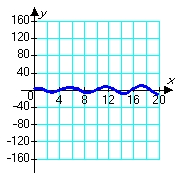
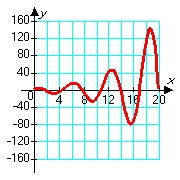
C)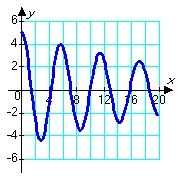
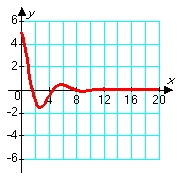
D)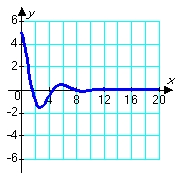
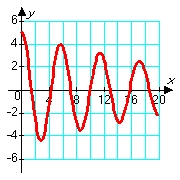
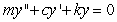 in which m, c, and k are positive constants. Which of the following pairs of graphs might correspond to the sets of constants m = 1.00, c = 0.80, and k = 1.20 (blue graph), and m = 1.00, c = 0.08, and k = 1.20 (red graph) ?
in which m, c, and k are positive constants. Which of the following pairs of graphs might correspond to the sets of constants m = 1.00, c = 0.80, and k = 1.20 (blue graph), and m = 1.00, c = 0.08, and k = 1.20 (red graph) ?A)


B)


C)


D)



Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
7
A spring is stretched 5 cm by a 1-kg mass. The mass is set in motion from its equilibrium position with an upward velocity of 2 m/s. The damping constant equals 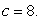 Find an equation for the position of the mass at any time t.
Find an equation for the position of the mass at any time t.
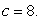 Find an equation for the position of the mass at any time t.
Find an equation for the position of the mass at any time t.
Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
8
Determine the form of a particular solution of the equation. 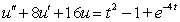
A)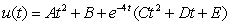
B)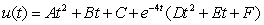
C)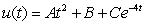
D)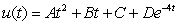
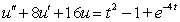
A)
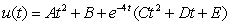
B)
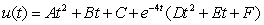
C)
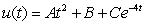
D)
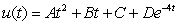

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
9
Identify the form of a particular solution to the equation 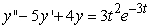 .
.
A)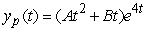
B)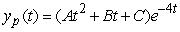
C)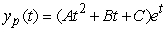
D)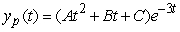
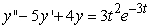 .
.A)
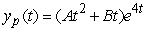
B)
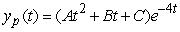
C)
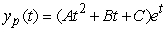
D)
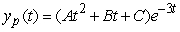

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
10
Find the general solution of 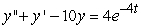 , given the particular solution
, given the particular solution 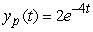 .
.
A)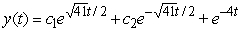
B)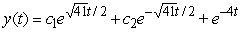
C)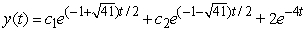
D)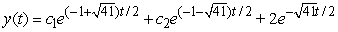
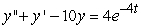 , given the particular solution
, given the particular solution 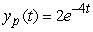 .
.A)
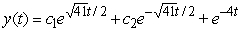
B)
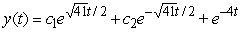
C)
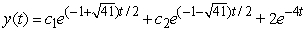
D)
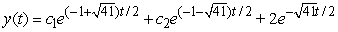

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the initial value problem 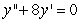 ,
, 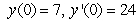 .
.
A)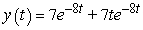
B)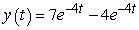
C)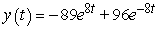
D)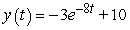
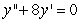 ,
, 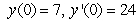 .
.A)
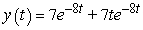
B)
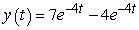
C)
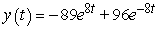
D)
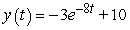

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
12
A certain spring is at rest when stretched 0.392 m by a 2.0 kg mass. Which function describes the motion of the mass if it is pulled down 0.25 m and released without imparting any initial velocity at time t = 0? Other helpful information: the motion is not damped; use 9.8 m s-2 as the acceleration due to gravity; and consider the zero position to be the rest position of the spring with the mass attached, and downward motion defines the positive x direction.
A)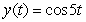
B)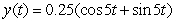
C)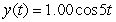
D)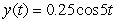
A)
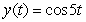
B)
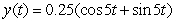
C)
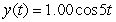
D)
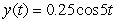

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
13
Identify the form of a particular solution to the equation 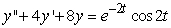 .
.
A)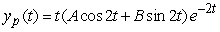
B)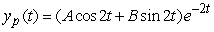
C)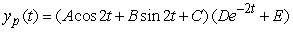
D)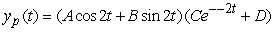
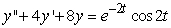 .
.A)
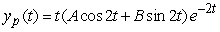
B)
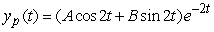
C)
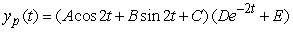
D)
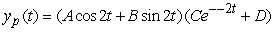

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
14
Find the general solution of 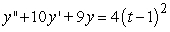 , given the particular solution
, given the particular solution 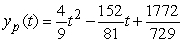 .
.
A)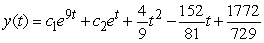
B)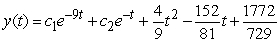
C)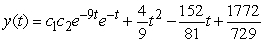
D)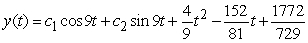
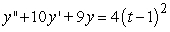 , given the particular solution
, given the particular solution 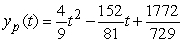 .
.A)
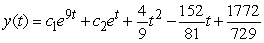
B)
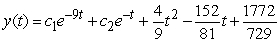
C)
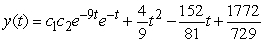
D)
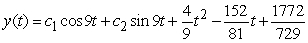

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
15
A 2.0 kg mass hangs on a spring with a 1.1 newton/meter force constant and its motion is not damped. If the system is subjected to an external variable-frequency vibration described as 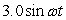 newtons, at what frequency,
newtons, at what frequency, 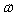 , will the external vibration and the spring system be in resonance?
, will the external vibration and the spring system be in resonance?
A) 0.55 s-1
B) 0.74 s-1
C) 1.82 s-1
D) 1.35 s-1
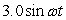 newtons, at what frequency,
newtons, at what frequency, 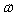 , will the external vibration and the spring system be in resonance?
, will the external vibration and the spring system be in resonance?A) 0.55 s-1
B) 0.74 s-1
C) 1.82 s-1
D) 1.35 s-1

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the initial value problem 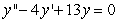 ,
, 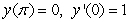 .
.
A)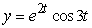
B)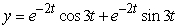
C)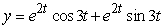
D)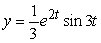
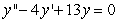 ,
, 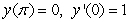 .
.A)
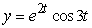
B)
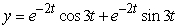
C)
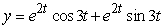
D)
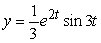

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
17
Find the general solution of the equation 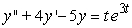 .
.
A)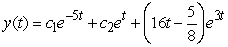
B)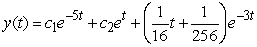
C)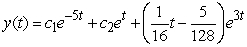
D)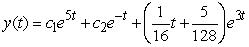
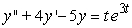 .
.A)
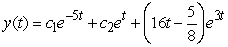
B)
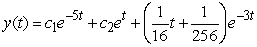
C)
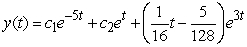
D)
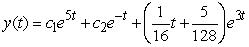

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
18
Find the general solution of the differential equation. 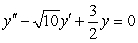
A)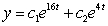
B)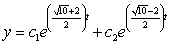
C)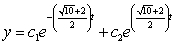
D)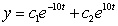
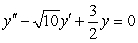
A)
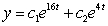
B)
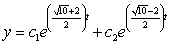
C)
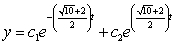
D)
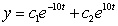

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
19
Identify the general solution of the the differential equation 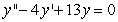 .
.
A)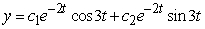
B)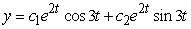
C)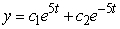
D)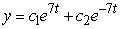
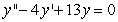 .
.A)
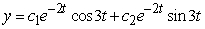
B)
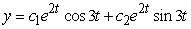
C)
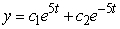
D)
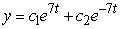

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
20
For 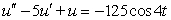 find the steady-state solution and identify its amplitude and phase shift.
find the steady-state solution and identify its amplitude and phase shift.
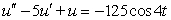 find the steady-state solution and identify its amplitude and phase shift.
find the steady-state solution and identify its amplitude and phase shift.
Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
21
A series circuit has a 0.15 henry inductor, a 350 ohm resistor, and a 0.00001 farad capacitor. There is an initial charge of 0.000001 coulombs, there is no initial current, and there is an applied voltage which is described as 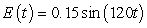 . Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
A)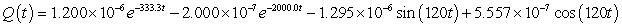
B)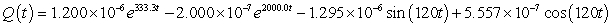
C)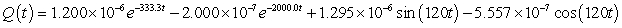
D)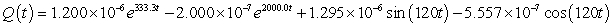
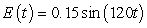 . Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.A)
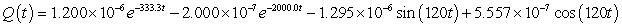
B)
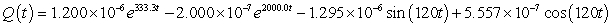
C)
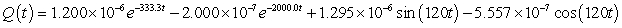
D)
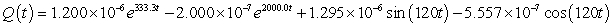

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
22
A second order differential equaiton can be arranged to the form 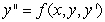 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is 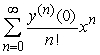 , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What does the fourth-degree Taylor polynomial look like for the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What does the fourth-degree Taylor polynomial look like for the solution to the equation 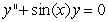 if the initial conditions are
if the initial conditions are 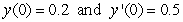 ?
?
A)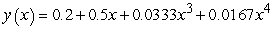
B)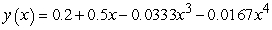
C)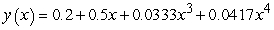
D)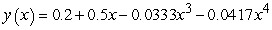
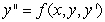 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is 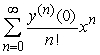 , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What does the fourth-degree Taylor polynomial look like for the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What does the fourth-degree Taylor polynomial look like for the solution to the equation 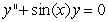 if the initial conditions are
if the initial conditions are 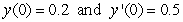 ?
?A)
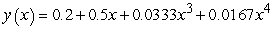
B)
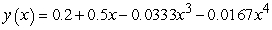
C)
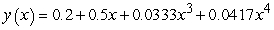
D)
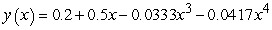

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
23
Find the recurrence relation for the general power series solution 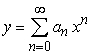 to the second order equation
to the second order equation 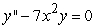 .
.
A)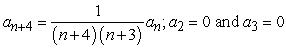
B)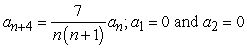
C)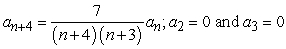
D)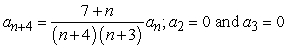
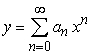 to the second order equation
to the second order equation 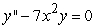 .
.A)
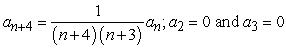
B)
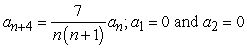
C)
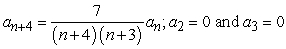
D)
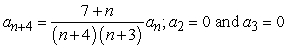

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
24
Suppose that the charge in a circuit satisfies the equation 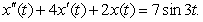 Find the gain of the circuit.
Find the gain of the circuit.
A)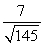
B)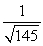
C)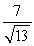
D)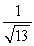
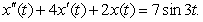 Find the gain of the circuit.
Find the gain of the circuit.A)
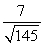
B)
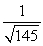
C)
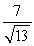
D)
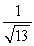

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
25
Identify the radius of convergence of the power series solutions about x = 0 of 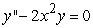 .
.
A)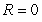
B)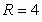
C)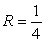
D)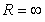
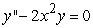 .
.A)
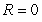
B)
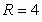
C)
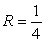
D)
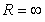

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
26
Identify the radius of convergence of the power series solutions about x = 0 of 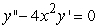 .
.
A) R = 0
B)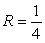
C) R =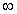
D) R = 4
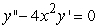 .
.A) R = 0
B)
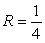
C) R =
D) R = 4

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the initial value problem 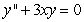 ,
, 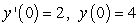 .
.
A)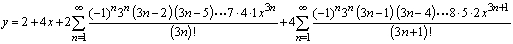
B)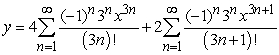
C)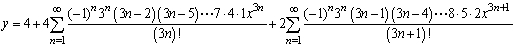
D)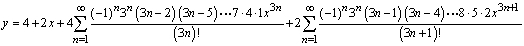
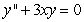 ,
, 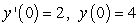 .
.A)
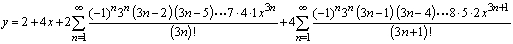
B)
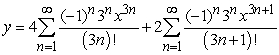
C)
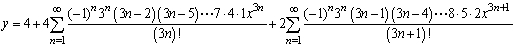
D)
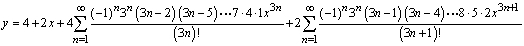

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
28
For a pendulum of weight 4 pounds, length 0.75 ft, damping constant ![<strong>For a pendulum of weight 4 pounds, length 0.75 ft, damping constant and forcing function find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s<sup>-2</sup>.]</strong> A) amplitude: 0.500 ft; period: 1.738 rad B) amplitude: 0.250 ft; period: 0.869 rad C) amplitude: 0.299 ft; period: 0.524 rad D) amplitude: 0.598 ft; period: 1.047 rad](https://storage.examlex.com/TB2342/11eaa948_cd6d_b591_84bc_476f4ce55b13_TB2342_11.jpg) and forcing function
and forcing function ![<strong>For a pendulum of weight 4 pounds, length 0.75 ft, damping constant and forcing function find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s<sup>-2</sup>.]</strong> A) amplitude: 0.500 ft; period: 1.738 rad B) amplitude: 0.250 ft; period: 0.869 rad C) amplitude: 0.299 ft; period: 0.524 rad D) amplitude: 0.598 ft; period: 1.047 rad](https://storage.examlex.com/TB2342/11eaa948_cd6d_b592_84bc_bb7c19e02aea_TB2342_11.jpg) find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s-2.]
find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s-2.]
A) amplitude: 0.500 ft; period: 1.738 rad
B) amplitude: 0.250 ft; period: 0.869 rad
C) amplitude: 0.299 ft; period: 0.524 rad
D) amplitude: 0.598 ft; period: 1.047 rad
![<strong>For a pendulum of weight 4 pounds, length 0.75 ft, damping constant and forcing function find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s<sup>-2</sup>.]</strong> A) amplitude: 0.500 ft; period: 1.738 rad B) amplitude: 0.250 ft; period: 0.869 rad C) amplitude: 0.299 ft; period: 0.524 rad D) amplitude: 0.598 ft; period: 1.047 rad](https://storage.examlex.com/TB2342/11eaa948_cd6d_b591_84bc_476f4ce55b13_TB2342_11.jpg) and forcing function
and forcing function ![<strong>For a pendulum of weight 4 pounds, length 0.75 ft, damping constant and forcing function find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s<sup>-2</sup>.]</strong> A) amplitude: 0.500 ft; period: 1.738 rad B) amplitude: 0.250 ft; period: 0.869 rad C) amplitude: 0.299 ft; period: 0.524 rad D) amplitude: 0.598 ft; period: 1.047 rad](https://storage.examlex.com/TB2342/11eaa948_cd6d_b592_84bc_bb7c19e02aea_TB2342_11.jpg) find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s-2.]
find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s-2.]A) amplitude: 0.500 ft; period: 1.738 rad
B) amplitude: 0.250 ft; period: 0.869 rad
C) amplitude: 0.299 ft; period: 0.524 rad
D) amplitude: 0.598 ft; period: 1.047 rad

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
29
A series circuit has a 0.2 henry inductor, a 490 ohm resistor, and a 0.000004 farad capacitor. There is an applied voltage which is described as 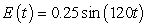 . Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.
A)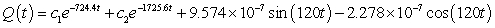
B)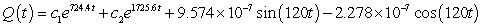
C)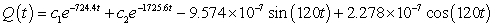
D)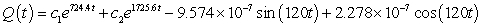
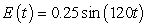 . Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.A)
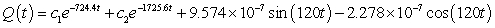
B)
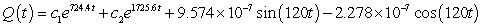
C)
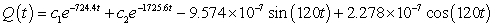
D)
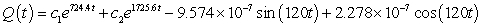

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
30
A series circuit has a 0.1 henry inductor, a 330 ohm resistor, and a 0.000009 farad capacitor. There is an initial charge of 0.000002 coulombs, there is no initial current, and there is an applied voltage which is described as 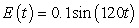 . Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
A)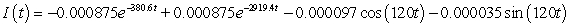
B)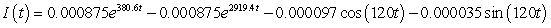
C)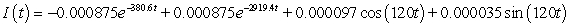
D)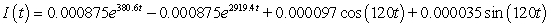
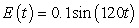 . Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.A)
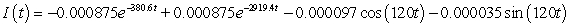
B)
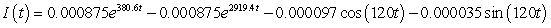
C)
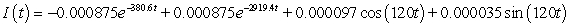
D)
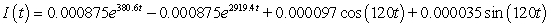

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
31
Identify the pair of graphs that correspond most closely to the solutions of ![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2ec8_84bc_5570d05417d2_TB2342_11.jpg) with
with ![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2ec9_84bc_afb08c789c05_TB2342_11.jpg) , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]
, respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]
A)![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2eca_84bc_ff244e133077_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2ecb_84bc_493932936daa_TB2342_11.jpg)
B)![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2ecc_84bc_c97536648cf1_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55dd_84bc_3bbe7d582c08_TB2342_11.jpg)
C)![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55de_84bc_a7f6458a0a32_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55df_84bc_c5e23f13c8d3_TB2342_11.jpg)
D)![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55e0_84bc_a188d53bfb41_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55e1_84bc_09178c24ff13_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2ec8_84bc_5570d05417d2_TB2342_11.jpg) with
with ![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2ec9_84bc_afb08c789c05_TB2342_11.jpg) , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]
, respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]A)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2eca_84bc_ff244e133077_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2ecb_84bc_493932936daa_TB2342_11.jpg)
B)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_2ecc_84bc_c97536648cf1_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55dd_84bc_3bbe7d582c08_TB2342_11.jpg)
C)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55de_84bc_a7f6458a0a32_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55df_84bc_c5e23f13c8d3_TB2342_11.jpg)
D)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55e0_84bc_a188d53bfb41_TB2342_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB2342/11eaa948_cd6c_55e1_84bc_09178c24ff13_TB2342_11.jpg)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
32
Find the recurrence relation for the general power series solution 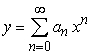 to the second order equation
to the second order equation 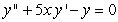 .
.
A)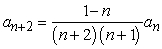
B)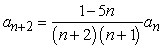
C)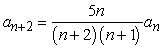
D)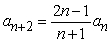
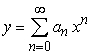 to the second order equation
to the second order equation 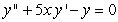 .
.A)
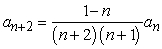
B)
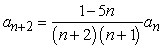
C)
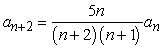
D)
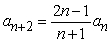

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
33
A pendulum has length 0.20 meter. A bob is released from rest from a starting angle ![<strong>A pendulum has length 0.20 meter. A bob is released from rest from a starting angle . Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s<sup>-2</sup>.]</strong> A) amplitude: 0.15 m; period: 0.898 rad B) amplitude: 0.15 m; period: 0.449 rad C) amplitude: 0.3 m; period: 0.449 rad D) amplitude: 0.3 m; period: 0.898 rad](https://storage.examlex.com/TB2342/11eaa948_cd6d_8e80_84bc_6901c6d16ffa_TB2342_11.jpg) . Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s-2.]
. Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s-2.]
A) amplitude: 0.15 m; period: 0.898 rad
B) amplitude: 0.15 m; period: 0.449 rad
C) amplitude: 0.3 m; period: 0.449 rad
D) amplitude: 0.3 m; period: 0.898 rad
![<strong>A pendulum has length 0.20 meter. A bob is released from rest from a starting angle . Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s<sup>-2</sup>.]</strong> A) amplitude: 0.15 m; period: 0.898 rad B) amplitude: 0.15 m; period: 0.449 rad C) amplitude: 0.3 m; period: 0.449 rad D) amplitude: 0.3 m; period: 0.898 rad](https://storage.examlex.com/TB2342/11eaa948_cd6d_8e80_84bc_6901c6d16ffa_TB2342_11.jpg) . Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s-2.]
. Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s-2.]A) amplitude: 0.15 m; period: 0.898 rad
B) amplitude: 0.15 m; period: 0.449 rad
C) amplitude: 0.3 m; period: 0.449 rad
D) amplitude: 0.3 m; period: 0.898 rad

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
34
A series circuit has an 0.1 henry inductor, a 300 ohm resistor, and a 10-4 farad capacitor. The initial charge on the capacitor is 10-6 coulombs, and there is no initial current nor applied voltage. Identify the function that describes the charge on the capacitor as a function of time.
A)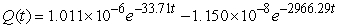
B)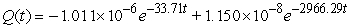
C)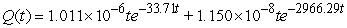
D)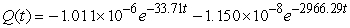
A)
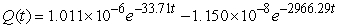
B)
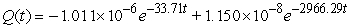
C)
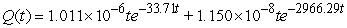
D)
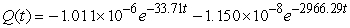

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
35
A second order differential equation can be arranged to the form 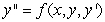 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 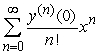 , one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation 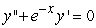 if the initial conditions are
if the initial conditions are 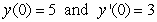 ?
?
A)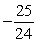
B)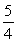
C)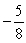
D)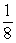
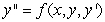 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 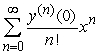 , one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation 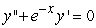 if the initial conditions are
if the initial conditions are 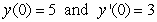 ?
?A)
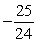
B)
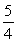
C)
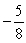
D)
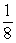

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
36
A series circuit has a 0.1 henry inductor, a 320 ohm resistor, and a 0.000006 farad capacitor. There is an initial charge of 0.000003 coulombs, there is no initial current, and there is an applied voltage which is described as 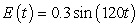 . Identify the steady-state solution to the differential equation.
. Identify the steady-state solution to the differential equation.
A)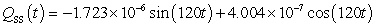
B)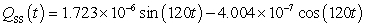
C)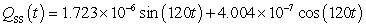
D)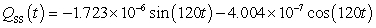
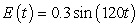 . Identify the steady-state solution to the differential equation.
. Identify the steady-state solution to the differential equation.A)
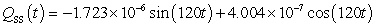
B)
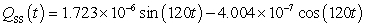
C)
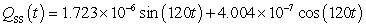
D)
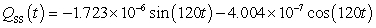

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the initial value problem 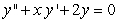 ,
, 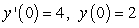 .
.
A)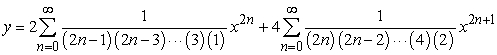
B)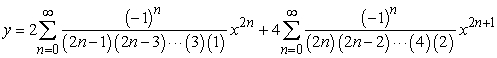
C)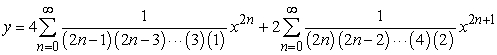
D)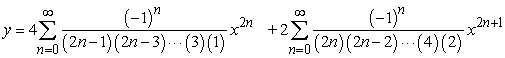
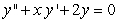 ,
, 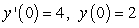 .
.A)
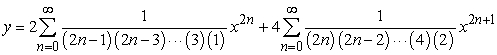
B)
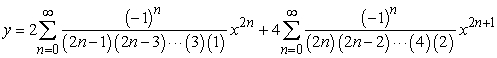
C)
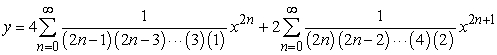
D)
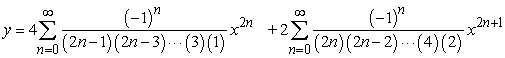

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
38
A series circuit has a 0.15 henry inductor, a 360 ohm resistor, and a 0.00001 farad capacitor. There is an initial charge of 0.000006 coulombs, there is no initial current, and there is an applied voltage which is described as 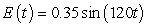 . Identify the amplitude of the steady-state solution.
. Identify the amplitude of the steady-state solution.
A) 0.000003
B) 0.000009
C) 0.35
D) 0.175
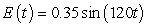 . Identify the amplitude of the steady-state solution.
. Identify the amplitude of the steady-state solution.A) 0.000003
B) 0.000009
C) 0.35
D) 0.175

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck


