Deck 4: Linear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/111
Play
Full screen (f)
Deck 4: Linear Programming
1
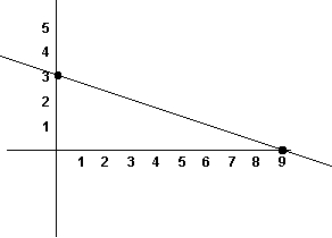
Sketch the graph of the equation x + 3y = 9.
2
Find the point of intersection for the lines represented by the equations 2x + 4y = 12 and 3x + y = 13.
(4, 1)
3
Write the constraint inequalities and the profit formula for this linear programming mixture problem: The Dig-the-Pig ham shop sells regular and special ham and cheese sandwiches. The regular is made of 5 oz of meat, 0.7 oz of cheese, and requires three minutes of preparation time. The special is made of 7 oz of meat, 0.6 oz of cheese, and requires 11 minutes of preparation time. The profit on a regular sandwich is 10 cents while the profit on a special sandwich is 40 cents. If Dig-the-Pig has 350 oz of meat, 42 oz of cheese, and 330 minutes of preparation time available each lunch period, how many of each type of sandwich should they try to sell to maximize profit?
x is the number of regular sandwiches made and y is the number of special sandwiches made.
Constraint inequalities: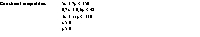 5x + 7y 3500.7x + 0.6y 42
5x + 7y 3500.7x + 0.6y 42
3x + 11y 330
x 0
y 0
Profit formula: P = 10x + 40y
P = 10x + 40y
Constraint inequalities:
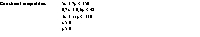 5x + 7y 3500.7x + 0.6y 42
5x + 7y 3500.7x + 0.6y 423x + 11y 330
x 0
y 0
Profit formula:
 P = 10x + 40y
P = 10x + 40y 4
Find the point of intersection for the lines represented by the equations 3x + 2y = 16 and 4x + 3y = 23.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
5
With the given constraints for the following linear programming mixture problem, graph the feasible region.  2 x + 3y 1800
2 x + 3y 1800
x 0
y 0
 2 x + 3y 1800
2 x + 3y 1800x 0
y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
6
Find the point of intersection for the lines represented by the equations 2x + 7y = 61 and 3x + 4y = 46.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
7
Describe a mixture problem.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
8
With the given constraints for the following linear programming mixture problem, graph the feasible region.  x + 3y 23
x + 3y 23
3x + 7y 50
x 2
y 4
 x + 3y 23
x + 3y 233x + 7y 50
x 2
y 4

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
9
Find the constraint inequalities and the profit formula for this linear programming mixture problem: The Acme Construction Company builds two types of houses. Plan A requires 200 man-hours for rough construction and 70 man-hours for finish work. Plan B requires 300 man-hours for rough construction and 50 man-hours for finish work. Acme has carpenters available to provide up to 900 hours of rough construction per month and 260 hours of finish work per month. If Acme clears $7000 profit on a Plan A house and $8000 profit on a Plan B house, how should they schedule production to maximize profit?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
10
With the given constraints for the following linear programming mixture problem, graph the feasible region.  x + 6y 1100
x + 6y 1100
4x + y 2100
x 0
y 0
 x + 6y 1100
x + 6y 11004x + y 2100
x 0
y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
11
Sketch the graph of the inequality 2x + 4y 12.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
12
Find the point of intersection for the lines represented by the equations 3x + 2y = 14 and 4x + 5y = 28.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
13
Sketch the graph of the inequality 5x + y 15.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
14
Sketch the graph of the inequality 4x + 6y 12.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
15
Find the constraint inequalities and the profit formula for this linear programming mixture problem: Toni has a small business producing dried floral wreaths and table arrangements. Each wreath takes seven hours to produce, uses 12 stems of flowers, and earns a profit of $23. Each table arrangement takes five hours to produce, uses 20 stems of flowers, and earns a profit of $26. Toni can work no more than 30 hours per week and has a steady supply of 100 stems of dried flowers per week. How should Toni schedule production to optimize profit?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
16
Write the constraint inequalities and the profit formula for this linear programming mixture problem: Amazin' Raisin Baking Co. makes both raisin cake and raisin pie. A batch of raisin cakes requires 5 lbs of flour, 2 lbs of sugar, and 1 lb of raisins. A batch of raisin pies requires 2 lbs of flour, 3 lbs of sugar, and 4 lbs of raisins. There are 165 lbs of flour, 110 lbs of sugar, and 120 lbs of raisins available each week. Standing orders require at least five batches of raisin cakes and eight batches of raisin pies per week. If profit on a batch of raisin cakes is $35 and profit on a batch of raisin pies is $40, how many batches of each should be made per week to maximize profit?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
17
With the given constraints for the following linear programming mixture problem, graph the feasible region.  2 x + 3y 180
2 x + 3y 180
5 x + 2y 230
x 0
y 0
 2 x + 3y 180
2 x + 3y 1805 x + 2y 230
x 0
y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
18
What is the goal of a linear programming?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
19
With the given constraints for the following linear programming mixture problem, graph the feasible region.  x + 6y 110
x + 6y 110
x 0
y 0
 x + 6y 110
x + 6y 110x 0
y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
20
Solve this linear programming mixture problem: Kim and Lynn produce pottery vases and bowls. A vase requires 25 oz of clay and 5 oz of glaze. A bowl requires 20 oz of clay and 10 oz of glaze. There are 500 oz of clay available and 160 oz of glaze available. The profit on one vase is $5 and the profit on one bowl is $3. How should Kim and Lynn schedule production to optimize profit?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
21
What type of solution does the Stepping Stone Method produce for the transportation problem?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
22
Solve this linear programming mixture problem: A small stereo manufacturer makes a receiver and a CD player. Each receiver takes eight hours to assemble, one hour to test and ship, and earns a profit of $30. Each CD player takes 15 hours to assemble, two hours to test and ship, and earns a profit of $50. There are 160 hours available in the assembly department and 26 hours available in the testing and shipping department. What should the production schedule be to maximize profit?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
23
In the optimal solution, how many units are shipped from supplier I to customer 2?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
24
Explain what the real world implications are if the optimal production policy for a linear programming mixture problem is represented by a point on the x-axis of the Cartesian plane.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
25
What is a tableau of a transportation problem?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
26
What is the indicator value of cell (III, 1)?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
27
Explain why the feasible region for a linear programming mixture problem must be in the first quadrant of the Cartesian plane.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
28
Name two alternatives to the graphical approach for solving linear programming problems.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
29
Find the point of intersection of the lines whose equations are 6x + 5y = 80 and 2x + y = 20.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
30
What is the indicator value of cell (II, 2)?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
31
What is the goal of a transportation problem?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
32
Find the maximum value of P, where P = 3x + 4y subject to the constraints:
x 0; y 0 ; x + 2y 8; x + y 5
x 0; y 0 ; x + 2y 8; x + y 5

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
33
Find the maximum value of P, where P = 100x + 10y subject to the constraints:
x 0; y 0 ; 2x + 5y 20; 2x + y 12
x 0; y 0 ; 2x + 5y 20; 2x + y 12

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
34
Fill in the blank: Given a transportation problem, a collection of circled cells is optimal if the value associated with each of the empty cells is positive.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
35
What is the cost of the optimal solution to this shipping problem?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
36
A solution for the transportation problem is optimal when the empty cells have what property?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
37
What type of solution does the Northwest Corner Rule produce for the transportation problem?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
38
What is the cost of the solution shown in the tableau above?

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
39
Describe the shape of the feasible region for linear programming mixture problems with two products.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
40
Explain why a linear programming mixture problem might have minimum constraints other than zero.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
41
Find the point of intersection of the lines with equations 4x + 2y = 12 and 3x + 9y = 39.
A) (5, -4)
B) (10, 1)
C) (1, 4)
D) (2, 2)
A) (5, -4)
B) (10, 1)
C) (1, 4)
D) (2, 2)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
42
Find the graph of the inequality 3x + 4y 12. 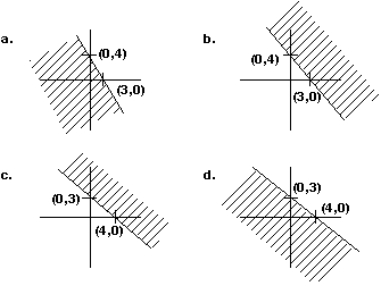


Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
43
Find the graph of the inequality 4x + 5y 40. 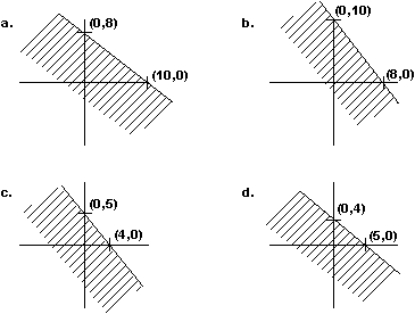


Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
44
Find the graph of the equation 4x + 6y = 18. 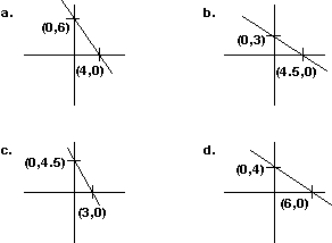


Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
45
Write a resource constraint for this situation: Producing a plastic ruler (x) requires 10 grams of plastic and producing a pencil box (y) requires 30 grams of plastic. There are 2000 grams of plastic available.
A) 200x + (2000/30)y 2000
B) 30x + 10y 2000
C) 10x + 30y 2000
D) x + y 2000
A) 200x + (2000/30)y 2000
B) 30x + 10y 2000
C) 10x + 30y 2000
D) x + y 2000

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
46
Find the graph of the inequality 3x + 7y 21. 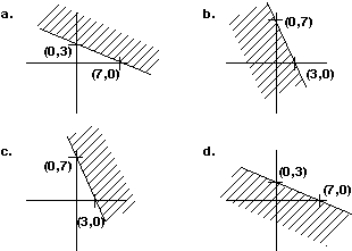


Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
47
Write the constraint inequalities for this situation: A cheeseburger (x) requires 5 oz of meat and 0.7 oz of cheese and a superburger (y) requires 7 oz of meat and 0.6 oz of cheese. The burger stand has 350 oz of meat and 42 oz of cheese available. The profit on a cheeseburger is 10 cents and the profit on a superburger is 40 cents.
A) 5x + 7y 350, 0.7 x + 0.6y 42, x 0, y 0
B) 5x + 0.7y 10, 7 x + 0.6y 40, x 0, y 0
C) 5x + 7y 10, 0.7 x + 0.6y 40, x 0, y 0
D) 70x + 50y 350, 60 x + 70y 42, x 0, y 0
A) 5x + 7y 350, 0.7 x + 0.6y 42, x 0, y 0
B) 5x + 0.7y 10, 7 x + 0.6y 40, x 0, y 0
C) 5x + 7y 10, 0.7 x + 0.6y 40, x 0, y 0
D) 70x + 50y 350, 60 x + 70y 42, x 0, y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
48
Find the point of intersection of the lines with equations 2x + 5y = 6 and 3x + 2y = 9.
A) (3, 0)
B) (2, 1)
C) (-3, 0)
D) (1, 2)
A) (3, 0)
B) (2, 1)
C) (-3, 0)
D) (1, 2)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
49
Find the graph of the inequality 6x + 4y 48. 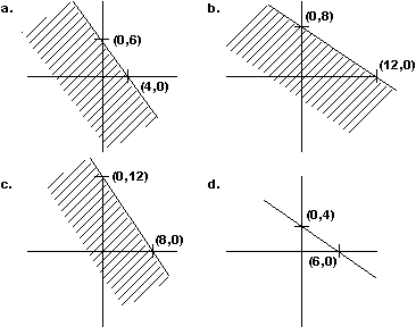


Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
50
Write the constraint inequalities for this situation: Kim and Lynn produce pottery vases and bowls. A vase requires 35 oz of clay and 5 oz of glaze. A bowl requires 20 oz of clay and 10 oz of glaze. There are 500 oz of clay available and 200 oz of glaze available. The profit on one vase is $5 and the profit on one bowl is $4.
A) 35x + 5y 5, 20 x + 10y 4, x 0, y 0
B) 35x + 5y 500, 20 x + 10y 200, x 0, y 0
C) 35x + 20y 500, 5 x + 10y 200, x 0, y 0
D) 35x + 20y $5, 5 x + 10y $4, x 0, y 0
A) 35x + 5y 5, 20 x + 10y 4, x 0, y 0
B) 35x + 5y 500, 20 x + 10y 200, x 0, y 0
C) 35x + 20y 500, 5 x + 10y 200, x 0, y 0
D) 35x + 20y $5, 5 x + 10y $4, x 0, y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
51
For a linear programming problem, the set/region is the collection of all physically possible solution choices that can be made.
A) population
B) sample
C) feasible
D) characteristic
A) population
B) sample
C) feasible
D) characteristic

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
52
Find the point of intersection of the lines with equations x + 4y = 11 and 2x + 5y = 16.
A) (2, 3)
B) (3, 2)
C) (6, 0)
D) (-2, 3)
A) (2, 3)
B) (3, 2)
C) (6, 0)
D) (-2, 3)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
53
Find the graph of the equation 5x + 2y = 15. 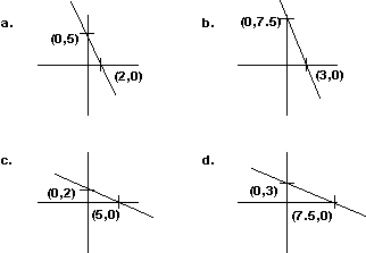


Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
54
Graph the constraint inequalities for a linear programming problem shown below. Which feasible region shown is correct? 
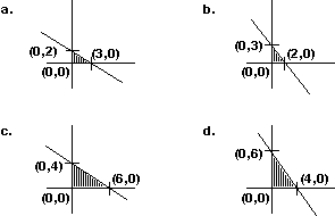



Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
55
Which of the following descriptions is NOT a correct common feature of mixture problem?
A) Definite resources are available in limited, known quantities for the period in question.
B) Definite products can be made by combining, or mixing the resources.
C) Each product's profit is contingent upon time.
D) The objective in a mixture problem is to find how much of each product to make so as to maximize the profit without exceeding any of the resource limitations.
A) Definite resources are available in limited, known quantities for the period in question.
B) Definite products can be made by combining, or mixing the resources.
C) Each product's profit is contingent upon time.
D) The objective in a mixture problem is to find how much of each product to make so as to maximize the profit without exceeding any of the resource limitations.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
56
Graph the constraint inequalities for a linear programming problem shown below. Which feasible region shown is correct? 
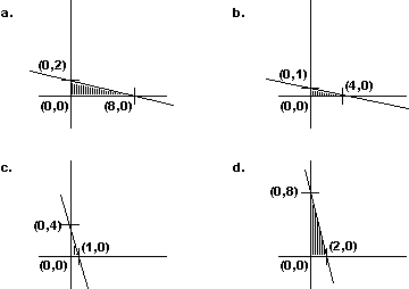



Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
57
Graph the constraint inequalities for a linear programming problem shown below. Which feasible region shown is correct? 
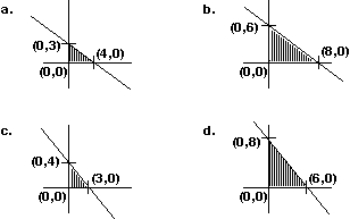



Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
58
Find the point of intersection of the lines with equations 3x + 2y = 21 and 2x + 1y = 13.
A) (5, 3)
B) (29, 45)
C) (8, -3)
D) (3, 5)
A) (5, 3)
B) (29, 45)
C) (8, -3)
D) (3, 5)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
59
Graph the constraint inequalities for a linear programming problem shown below. Which feasible region shown is correct? 
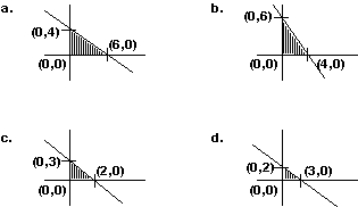



Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
60
Write a resource constraint for this situation: A lawn service company has 40 hours of worker time available. Mowing a lawn (x) takes three hours and trimming (y) takes two hours. The profit from mowing is $15 and the profit from trimming is $10.
A) 3x + 2y 40
B) (40/3)x + 10y 40
C) 15x + 10y 40
D) 5x + 5y 40
A) 3x + 2y 40
B) (40/3)x + 10y 40
C) 15x + 10y 40
D) 5x + 5y 40

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
61
Write a profit formula for this mixture problem: A small stereo manufacturer makes a receiver (x) and a CD player (y). Each receiver takes eight hours to assemble, one hour to test and ship, and earns a profit of $30. Each CD player takes 15 hours to assemble, two hours to test and ship, and earns a profit of $50. There are 160 hours available in the assembly department and 22 hours available in the testing and shipping department.
A) P = 8x + 1y
B) P = 160x + 22y
C) P = 15x + 2y
D) P = 30x + 50y
A) P = 8x + 1y
B) P = 160x + 22y
C) P = 15x + 2y
D) P = 30x + 50y

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
62
The graph of the feasible region for a mixture problem is shown below. Find the point that maximizes the profit function P = 2x + y. 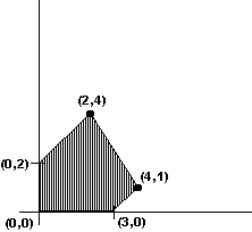
A) (0, 2)
B) (2, 4)
C) (4, 1)
D) (3, 0)

A) (0, 2)
B) (2, 4)
C) (4, 1)
D) (3, 0)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
63
Write the resource constraints for this situation: A company manufactures patio chairs (x) and rockers (y). Each piece is made of wood, plastic, and aluminum. A chair requires one unit of wood, one unit of plastic, and two units of aluminum. A rocker requires one unit of wood, two units of plastic, and five units of aluminum. The company's profit on a chair is $7 and on a rocker is $12. The company has available 400 units of wood, 500 units of plastic, and 1450 units of aluminum.
A) 1x + 1y + 2z 7, 1x + 2y + 5z 12, x 0, y 0, z 0
B) 1x + 1y 400, 1 x + 2y 500, 2x + 5y 1450, x 0, y 0
C) 400x + 500y + 1450z 0, 1x + 1y + 2z 7, 1x+ 2y + 5z 12, x 0, y 0, z 0
D) 7x + 12y 400, 2 x + 5y 1450, x 0, y 0
A) 1x + 1y + 2z 7, 1x + 2y + 5z 12, x 0, y 0, z 0
B) 1x + 1y 400, 1 x + 2y 500, 2x + 5y 1450, x 0, y 0
C) 400x + 500y + 1450z 0, 1x + 1y + 2z 7, 1x+ 2y + 5z 12, x 0, y 0, z 0
D) 7x + 12y 400, 2 x + 5y 1450, x 0, y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
64
The graph of the feasible region for a mixture problem is shown below. Find the point that maximizes the profit function P = 2x + 3y. 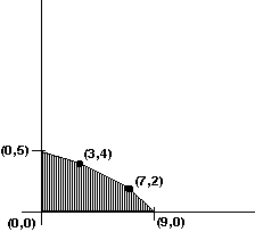
A) (0, 5)
B) (3, 4)
C) (7, 2)
D) (9, 0)

A) (0, 5)
B) (3, 4)
C) (7, 2)
D) (9, 0)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
65
Write a profit formula for this mixture problem: Kim and Lynn produce pottery vases (x) and bowls (y). A vase requires 35 oz of clay and 5 oz of glaze. A bowl requires 20 oz of clay and 10 oz of glaze. There are 500 oz of clay available and 200 oz of glaze available. The profit on one vase is $5 and the profit on one bowl is $4.
A) P = 500x + 200y
B) P = 35x + 20y
C) P = 5x + 4y
D) P = 5x + 10y
A) P = 500x + 200y
B) P = 35x + 20y
C) P = 5x + 4y
D) P = 5x + 10y

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
66
Graph the feasible region identified by the inequalities: 
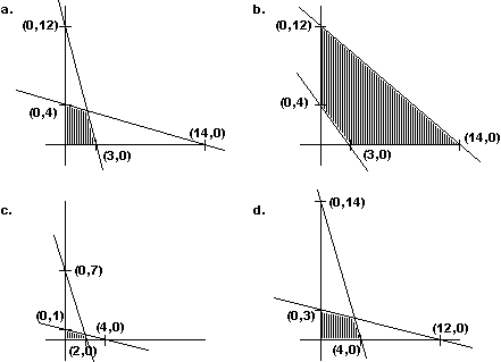



Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
67
Given below is the sketch of the feasible region in a linear programming problem. Which point is NOT in the feasible region? 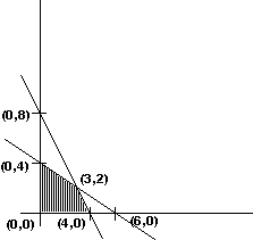
A) (0, 4)
B) (4, 0)
C) (6, 0)
D) (1, 2)

A) (0, 4)
B) (4, 0)
C) (6, 0)
D) (1, 2)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
68
Write the resource constraints for this situation: Kim and Lynn produce tables (x) and chairs (y). Each piece is assembled, sanded, and stained. A table requires two hours to assemble, three hours to sand, and three hours to stain. A chair requires four hours to assemble, two hours to sand, and three hours to stain. The profit earned on each table is $20 and on each chair is $12. Together Kim and Lynn spend at most 16 hours assembling, 10 hours sanding, and 13 hours staining.
A) 2x + 4y 16, 3 x + 2y 10, 3x + 3y 13, x 0, y 0
B) 2x + 3y + 3z 20, 4x + 2y + 3z 12, x 0, y 0, z 0
C) 16x + 10y + 13z 0, 2x + 3y + 3z 20, 4x + 2y + 3z 12, x 0, y 0, z 0
D) 8x + 4y 16, (10/3) x + 5y 10, (13/3)x + (13/3)y 13, x 0, y 0
A) 2x + 4y 16, 3 x + 2y 10, 3x + 3y 13, x 0, y 0
B) 2x + 3y + 3z 20, 4x + 2y + 3z 12, x 0, y 0, z 0
C) 16x + 10y + 13z 0, 2x + 3y + 3z 20, 4x + 2y + 3z 12, x 0, y 0, z 0
D) 8x + 4y 16, (10/3) x + 5y 10, (13/3)x + (13/3)y 13, x 0, y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
69
Graph the feasible region identified by the inequalities: 
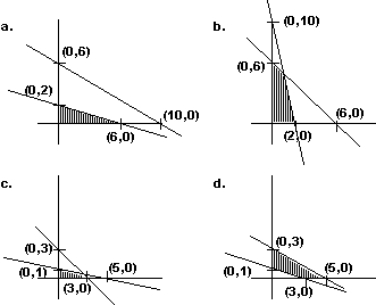



Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
70
Given below is the sketch of the feasible region in a linear programming problem. Which point is NOT in the feasible region? 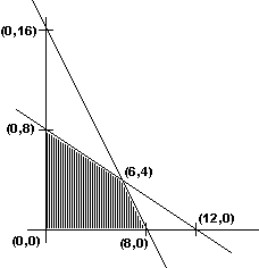
A) (0, 8)
B) (12, 0)
C) (6, 4)
D) (2, 2)

A) (0, 8)
B) (12, 0)
C) (6, 4)
D) (2, 2)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
71
Graph the feasible region identified by the inequalities: 
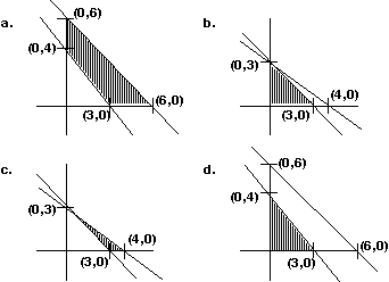



Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
72
Write a profit formula for this mixture problem: Kim and Lynn produce tables (x) and chairs (y). Each piece is assembled, sanded, and stained. A table requires two hours to assemble, three hours to sand, and three hours to stain. A chair requires four hours to assemble, two hours to sand, and three hours to stain. The profit earned on each table is $20 and on each chair is $12. Together Kim and Lynn spend at most 16 hours assembling, 10 hours sanding, and 13 hours staining.
A) P = 20x + 12y
B) P = 2x + 3y + 3z
C) P = 16x + 10y + 13z
D) P = 8x + 9y
A) P = 20x + 12y
B) P = 2x + 3y + 3z
C) P = 16x + 10y + 13z
D) P = 8x + 9y

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
73
Given below is the sketch of the feasible region in a linear programming problem. Which point is NOT in the feasible region? 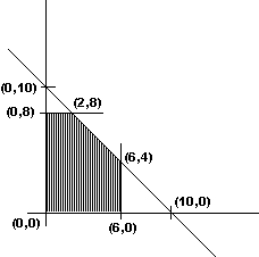
A) (6, 4)
B) (0, 10)
C) (2, 6)
D) (0, 8)

A) (6, 4)
B) (0, 10)
C) (2, 6)
D) (0, 8)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
74
Graph the feasible region identified by the inequalities: 
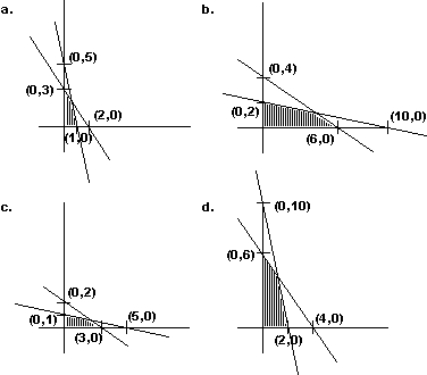



Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
75
The graph of the feasible region for a mixture problem is shown below. Find the point that maximizes the profit function P = 3x + 6y. 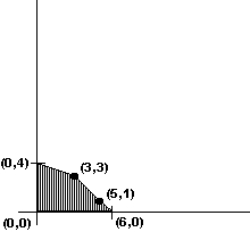
A) (0, 4)
B) (3, 3)
C) (5, 1)
D) (6, 0)

A) (0, 4)
B) (3, 3)
C) (5, 1)
D) (6, 0)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
76
Write the resource constraints for this situation: A small stereo manufacturer makes a receiver and a CD player. Each receiver (x) takes eight hours to assemble and eight hours to test and ship. Each CD player (y) takes 15 hours to assemble and two hours to test and ship. The profit on each receiver is $30 and the profit on each CD player is $50. There are 160 hours available in the assembly department and 22 hours available in the testing and shipping department.
A) 8x + 1y 30, 15x + 2y 50, x 0, y 0
B) 8x + 1y 160, 15x + 2y 22, x 0, y 0
C) 8x + 15y 30, 8x + 2y 50, x 0, y 0
D) 8x + 15y 160, 8x + 2y 22, x 0, y 0
A) 8x + 1y 30, 15x + 2y 50, x 0, y 0
B) 8x + 1y 160, 15x + 2y 22, x 0, y 0
C) 8x + 15y 30, 8x + 2y 50, x 0, y 0
D) 8x + 15y 160, 8x + 2y 22, x 0, y 0

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
77
Given below is the sketch of the feasible region in a linear programming problem. Which point is NOT in the feasible region? 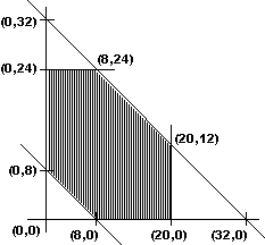
A) (0, 32)
B) (0, 24)
C) (8, 16)
D) (20, 12)

A) (0, 32)
B) (0, 24)
C) (8, 16)
D) (20, 12)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
78
Write a profit formula for this mixture problem: A company manufactures patio chairs (x) and rockers (y). Each piece is made of wood, plastic, and aluminum. A chair requires one unit of wood, one unit of plastic, and two units of aluminum. A rocker requires one unit of wood, two units of plastic, and five units of aluminum. The company's profit on a chair is $7 and on a rocker is $12. The company has available 400 units of wood, 500 units of plastic, and 1450 units of aluminum.
A) P = 400x + 500y + 1450z
B) P = 4x + 8y
C) P = 7x + 12y
D) P = 1x + 2y + 5z
A) P = 400x + 500y + 1450z
B) P = 4x + 8y
C) P = 7x + 12y
D) P = 1x + 2y + 5z

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
79
The graph of the feasible region for a mixture problem is shown below. Find the point that maximizes the profit function P = x + 4y. 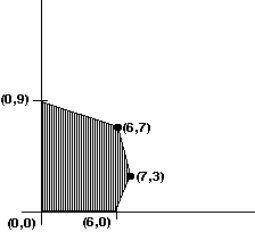
A) (0, 9)
B) (6, 7)
C) (7, 3)
D) (6, 0)

A) (0, 9)
B) (6, 7)
C) (7, 3)
D) (6, 0)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
80
Given below is the sketch of the feasible region in a linear programming problem. Which point is NOT in the feasible region? 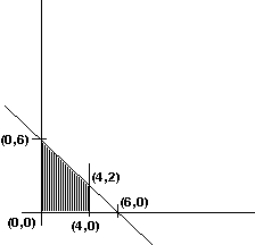
A) (0, 6)
B) (4, 0)
C) (4, 2)
D) (6, 0)

A) (0, 6)
B) (4, 0)
C) (4, 2)
D) (6, 0)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck


