Deck 2: Introduction to Optimization and Linear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/76
Play
Full screen (f)
Deck 2: Introduction to Optimization and Linear Programming
1
In mathematical programming formulations the objective function may contain cubic terms.
False
2
A set of values for the decision variables that satisfy all the constraints and yields the best objective function value is
A) a feasible solution.
B) an optimal solution.
C) a corner point solution.
D) both (a) and (c).
A) a feasible solution.
B) an optimal solution.
C) a corner point solution.
D) both (a) and (c).
an optimal solution.
3
The second step in formulating a linear programming problem is
A) Identify any upper or lower bounds on the decision variables.
B) State the constraints as linear combinations of the decision variables.
C) Understand the problem.
D) Identify the decision variables.
E) State the objective function as a linear combination of the decision variables.
A) Identify any upper or lower bounds on the decision variables.
B) State the constraints as linear combinations of the decision variables.
C) Understand the problem.
D) Identify the decision variables.
E) State the objective function as a linear combination of the decision variables.
Identify the decision variables.
4
The best way of solving LP problems is to apply managerial intuition regarding the levels of decision variables.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
5
The following linear programming problem has been written to plan the production of two products. The company wants to maximize its profits. X1 = number of product 1 produced in each batch
X2 = number of product 2 produced in each batch How much profit is earned per each unit of product 2 produced?
How much profit is earned per each unit of product 2 produced?
A) 150
B) 175
C) 200
D) 250
X2 = number of product 2 produced in each batch
 How much profit is earned per each unit of product 2 produced?
How much profit is earned per each unit of product 2 produced?A) 150
B) 175
C) 200
D) 250

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
6
When do alternate optimal solutions occur in LP models?
A) When a binding constraint is parallel to a level curve.
B) When a non-binding constraint is perpendicular to a level curve.
C) When a constraint is parallel to another constraint.
D) Alternate optimal solutions indicate an infeasible condition.
A) When a binding constraint is parallel to a level curve.
B) When a non-binding constraint is perpendicular to a level curve.
C) When a constraint is parallel to another constraint.
D) Alternate optimal solutions indicate an infeasible condition.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
7
A facility produces two products. The labor constraint (in hours) is formulated as: 350x1+300x2 ≤ 10,000. The number 10,000 represents
A) a profit contribution of one unit of product 1.
B) one unit of product 1 uses 10,000 hours of labor.
C) there are 10,000 hours of labor available for use.
D) the problem has no objective function.
A) a profit contribution of one unit of product 1.
B) one unit of product 1 uses 10,000 hours of labor.
C) there are 10,000 hours of labor available for use.
D) the problem has no objective function.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
8
How much money should an individual withdraw each year from various retirement accounts is an example of a constraint.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
9
Limited resources are modeled in optimization problems as
A) an objective function.
B) constraints.
C) decision variables.
D) alternatives.
A) an objective function.
B) constraints.
C) decision variables.
D) alternatives.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
10
The constraint for resource 1 is 5 X1 + 4 X2 ≤ 200. If X1 = 20, what it the maximum value for X2?
A) 20
B) 25
C) 40
D) 50
A) 20
B) 25
C) 40
D) 50

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following is the general format of an objective function?
A) f(X1, X2, ..., Xn) ≤ b
B) f(X1, X2, ..., Xn) ≥ b
C) f(X1, X2, ..., Xn) = b
D) f(X1, X2, ..., Xn)
A) f(X1, X2, ..., Xn) ≤ b
B) f(X1, X2, ..., Xn) ≥ b
C) f(X1, X2, ..., Xn) = b
D) f(X1, X2, ..., Xn)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
12
The desire to maximize profits is an example of a(n)
A) decision.
B) constraint.
C) objective.
D) parameter.
A) decision.
B) constraint.
C) objective.
D) parameter.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
13
The objective function coefficients represent per unit objective function contributions from one unit of the associated decision variables.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
14
The decisions in an optimization problem are often represented in a mathematical model by the symbols X1, X2, …, Xn.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
15
Linear programming problems have
A) linear objective functions, non-linear constraints.
B) non-linear objective functions, non-linear constraints.
C) non-linear objective functions, linear constraints.
D) linear objective functions, linear constraints.
A) linear objective functions, non-linear constraints.
B) non-linear objective functions, non-linear constraints.
C) non-linear objective functions, linear constraints.
D) linear objective functions, linear constraints.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
16
A diet is being developed which must contain at least 100 mg of vitamin C. Two fruits are used in this diet. Bananas contain 30 mg of vitamin C and Apples contain 20 mg of vitamin C. The diet must contain at least 100 mg of vitamin C. Which of the following constraints reflects the relationship between Bananas, Apples and vitamin C?
A) 20 A + 30 B ≥ 100
B) 20 A + 30 B ≤ 100
C) 20 A + 30 B = 100
D) 20 A = 100
A) 20 A + 30 B ≥ 100
B) 20 A + 30 B ≤ 100
C) 20 A + 30 B = 100
D) 20 A = 100

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
17
An extreme point of the feasible region can include negative values of coordinates.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
18
A redundant constraint is one which
A) plays no role in determining the feasible region of the problem.
B) is parallel to the level curve.
C) is added after the problem is already formulated.
D) can only increase the objective function value.
A) plays no role in determining the feasible region of the problem.
B) is parallel to the level curve.
C) is added after the problem is already formulated.
D) can only increase the objective function value.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
19
Mathematical programming is an approach that involves determining how to allocate the resources in such a way as to maximize profits or minimize costs.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
20
The first step in formulating an LP model is determining the decision variables.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
21
The third step in formulating a linear programming problem is
A) Identify any upper or lower bounds on the decision variables.
B) State the constraints as linear combinations of the decision variables.
C) Understand the problem.
D) Identify the decision variables.
E) State the objective function as a linear combination of the decision variables.
A) Identify any upper or lower bounds on the decision variables.
B) State the constraints as linear combinations of the decision variables.
C) Understand the problem.
D) Identify the decision variables.
E) State the objective function as a linear combination of the decision variables.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
22
For an infeasible problem, the feasible region:
A) is an empty set
B) has infinite number of feasible solutions
C) has only one optimal solution
D) is unbounded
A) is an empty set
B) has infinite number of feasible solutions
C) has only one optimal solution
D) is unbounded

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
23
The constraint for resource 1 is 5 X1 + 4 X2 ≥ 200. If X1 = 40 and X2 = 20, how many additional units, if any, of resource 1 are employed above the minimum of 200?
A) 0
B) 20
C) 40
D) 80
A) 0
B) 20
C) 40
D) 80

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
24
A facility produces two products. The labor constraint (in hours) is formulated as: 350x1+300x2 ≤ 10,000. The number 350 means that
A) one unit of product 1 contributes $350 to the objective function.
B) one unit of product 1 uses 350 hours of labor.
C) the problem is unbounded.
D) the problem has no objective function.
A) one unit of product 1 contributes $350 to the objective function.
B) one unit of product 1 uses 350 hours of labor.
C) the problem is unbounded.
D) the problem has no objective function.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
25
If there is no way to simultaneously satisfy all the constraints in an LP model the problem is said to be
A) infeasible.
B) open ended.
C) multi-optimal.
D) unbounded.
A) infeasible.
B) open ended.
C) multi-optimal.
D) unbounded.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
26
Mathematical programming is referred to as
A) optimization.
B) satisficing.
C) approximation.
D) simulation.
A) optimization.
B) satisficing.
C) approximation.
D) simulation.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
27
The symbols X1, Z1, Dog are all examples of
A) decision variables.
B) constraints.
C) objectives.
D) parameters.
A) decision variables.
B) constraints.
C) objectives.
D) parameters.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
28
This graph shows the feasible region (defined by points ACDEF) and objective function level curve (BG) for a maximization problem. Which point corresponds to the optimal solution to the problem? 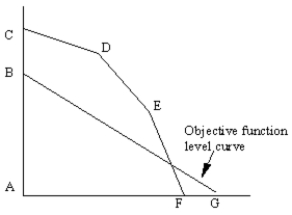
A) A
B) B
C) C
D) D
E) E

A) A
B) B
C) C
D) D
E) E

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
29
The first step in formulating a linear programming problem is
A) Identify any upper or lower bounds on the decision variables.
B) State the constraints as linear combinations of the decision variables.
C) Understand the problem.
D) Identify the decision variables.
E) State the objective function as a linear combination of the decision variables.
A) Identify any upper or lower bounds on the decision variables.
B) State the constraints as linear combinations of the decision variables.
C) Understand the problem.
D) Identify the decision variables.
E) State the objective function as a linear combination of the decision variables.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
30
The number of units to ship from Chicago to Memphis is an example of a(n)
A) decision.
B) constraint.
C) objective.
D) parameter.
A) decision.
B) constraint.
C) objective.
D) parameter.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
31
A facility produces two products and wants to maximize profit. The objective function to maximize is z=350x1+300x2. The number 350 means that:
A) one unit of product 1 contributes $350 to the objective function
B) one unit of product 1 contributes $300 to the objective function
C) the problem is unbounded
D) the problem has no constraints
A) one unit of product 1 contributes $350 to the objective function
B) one unit of product 1 contributes $300 to the objective function
C) the problem is unbounded
D) the problem has no constraints

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
32
The following linear programming problem has been written to plan the production of two products. The company wants to maximize its profits. X1 = number of product 1 produced in each batch
X2 = number of product 2 produced in each batch How much profit is earned if the company produces 10 units of product 1 and 5 units of product 2?
How much profit is earned if the company produces 10 units of product 1 and 5 units of product 2?
A) 750
B) 2500
C) 2750
D) 3250
X2 = number of product 2 produced in each batch
 How much profit is earned if the company produces 10 units of product 1 and 5 units of product 2?
How much profit is earned if the company produces 10 units of product 1 and 5 units of product 2?A) 750
B) 2500
C) 2750
D) 3250

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
33
A manager has only 200 tons of plastic for his company. This is an example of a(n)
A) decision.
B) constraint.
C) objective.
D) parameter.
A) decision.
B) constraint.
C) objective.
D) parameter.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
34
What is the goal in optimization?
A) Find the decision variable values that result in the best objective function and satisfy all constraints.
B) Find the values of the decision variables that use all available resources.
C) Find the values of the decision variables that satisfy all constraints.
D) None of these.
A) Find the decision variable values that result in the best objective function and satisfy all constraints.
B) Find the values of the decision variables that use all available resources.
C) Find the values of the decision variables that satisfy all constraints.
D) None of these.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
35
The following diagram shows the constraints for a LP model. Assume the point (0,0) satisfies constraint (B,J) but does not satisfy constraints (D,H) or (C,I). Which set of points on this diagram defines the feasible solution space? 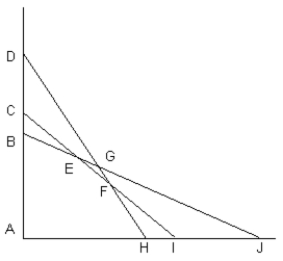
A) A, B, E, F, H
B) A, D, G, J
C) F, G, H, J
D) I, F, G, J

A) A, B, E, F, H
B) A, D, G, J
C) F, G, H, J
D) I, F, G, J

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
36
Most individuals manage their individual retirement accounts (IRAs) so they
A) maximize the amount of money they withdraw.
B) minimize the amount of taxes they must pay.
C) retire with a minimum amount of money.
D) leave all their money to the government.
A) maximize the amount of money they withdraw.
B) minimize the amount of taxes they must pay.
C) retire with a minimum amount of money.
D) leave all their money to the government.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following actions would expand the feasible region of an LP model?
A) Loosening the constraints.
B) Tightening the constraints.
C) Multiplying each constraint by 2.
D) Adding an additional constraint.
A) Loosening the constraints.
B) Tightening the constraints.
C) Multiplying each constraint by 2.
D) Adding an additional constraint.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
38
A linear formulation means that:
A) the objective function and all constraints must be linear
B) only the objective function must be linear
C) at least one constraint must be linear
D) no more than 50% of the constraints must be linear
A) the objective function and all constraints must be linear
B) only the objective function must be linear
C) at least one constraint must be linear
D) no more than 50% of the constraints must be linear

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
39
What are the three common elements of an optimization problem?
A) objectives, resources, goals.
B) decisions, constraints, an objective.
C) decision variables, profit levels, costs.
D) decisions, resource requirements, a profit function.
A) objectives, resources, goals.
B) decisions, constraints, an objective.
C) decision variables, profit levels, costs.
D) decisions, resource requirements, a profit function.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
40
If constraints are added to an LP model the feasible solution space will generally
A) decrease.
B) increase.
C) remain the same.
D) become more feasible.
A) decrease.
B) increase.
C) remain the same.
D) become more feasible.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
41
A company makes two products, X1 and X2. They require at least 20 of each be produced. Which set of lower bound constraints reflect this requirement?
A) X1 ≥ 20, X2 ≥ 20
B) X1 + X2 ≥ 20
C) X1 + X2 ≥ 40
D) X1 ≥ 20, X2 ≥ 20, X1 + X2 ≤ 40
A) X1 ≥ 20, X2 ≥ 20
B) X1 + X2 ≥ 20
C) X1 + X2 ≥ 40
D) X1 ≥ 20, X2 ≥ 20, X1 + X2 ≤ 40

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
42
If a problem has infinite number solutions, the objective function
A) is parallel to one of the binding constraints.
B) goes through exactly one corner point of the feasible region.
C) cannot identify a feasible region.
D) is infeasible.
A) is parallel to one of the binding constraints.
B) goes through exactly one corner point of the feasible region.
C) cannot identify a feasible region.
D) is infeasible.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
43
Why do we study the graphical method of solving LP problems?
A) Lines are easy to draw on paper.
B) To develop an understanding of the linear programming strategy.
C) It is faster than computerized methods.
D) It provides better solutions than computerized methods.
A) Lines are easy to draw on paper.
B) To develop an understanding of the linear programming strategy.
C) It is faster than computerized methods.
D) It provides better solutions than computerized methods.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
44
The constraints of an LP model define the
A) feasible region
B) practical region
C) maximal region
D) opportunity region
A) feasible region
B) practical region
C) maximal region
D) opportunity region

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
45
When the objective function can increase without ever contacting a constraint the LP model is said to be
A) infeasible.
B) open ended.
C) multi-optimal.
D) unbounded.
A) infeasible.
B) open ended.
C) multi-optimal.
D) unbounded.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
46
Suppose that a constraint 2x1+3x2 ≥ 900 is binding. Then, a constraint 4x1+6x2 ≥ 600 is
A) redundant.
B) binding.
C) limiting.
D) infeasible.
A) redundant.
B) binding.
C) limiting.
D) infeasible.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
47
A production optimization problem has 4 decision variables and a requirement that at least b1 units of material 1 are consumed. Which of the following constraints reflects this fact?
A) f(X1, X2, X3, X4) ≤ b1
B) f(X1, X2, X3, X4) ≥ b1
C) f(X1, X2, X3, X4) = b1
D) f(X1, X2, X3, X4) ≠ b1
A) f(X1, X2, X3, X4) ≤ b1
B) f(X1, X2, X3, X4) ≥ b1
C) f(X1, X2, X3, X4) = b1
D) f(X1, X2, X3, X4) ≠ b1

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
48
Level curves are used when solving LP models using the graphical method. To what part of the model do level curves relate?
A) constraints
B) boundaries
C) right hand sides
D) objective function
A) constraints
B) boundaries
C) right hand sides
D) objective function

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
49
The objective function for a LP model is 3 X1 + 2 X2. If X1 = 20 and X2 = 30, what is the value of the objective function?
A) 0
B) 50
C) 60
D) 120
A) 0
B) 50
C) 60
D) 120

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
50
A common objective in the product mix problem is
A) maximizing cost.
B) maximizing profit.
C) minimizing production time.
D) maximizing production volume.
A) maximizing cost.
B) maximizing profit.
C) minimizing production time.
D) maximizing production volume.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
51
In a mathematical formulation of an optimization problem, the objective function is written as z=2x1+3x2. Then:
A) x1 is a decision variable
B) x2 is a parameter
C) z needs to be maximized
D) 2 is a first decision variable level
A) x1 is a decision variable
B) x2 is a parameter
C) z needs to be maximized
D) 2 is a first decision variable level

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
52
Which of the following special conditions in an LP model represent potential errors in the mathematical formulation?
A) Alternate optimum solutions and infeasibility
B) Redundant constraints and unbounded solutions
C) Infeasibility and unbounded solutions
D) Alternate optimum solutions and redundant constraints
A) Alternate optimum solutions and infeasibility
B) Redundant constraints and unbounded solutions
C) Infeasibility and unbounded solutions
D) Alternate optimum solutions and redundant constraints

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
53
A production optimization problem has 4 decision variables and resource 1 limits how many of the 4 products can be produced. Which of the following constraints reflects this fact?
A) f(X1, X2, X3, X4) ≤ b1
B) f(X1, X2, X3, X4) ≥ b1
C) f(X1, X2, X3, X4) = b1
D) f(X1, X2, X3, X4) ≠ b1
A) f(X1, X2, X3, X4) ≤ b1
B) f(X1, X2, X3, X4) ≥ b1
C) f(X1, X2, X3, X4) = b1
D) f(X1, X2, X3, X4) ≠ b1

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
54
A company uses 4 pounds of resource 1 to make each unit of X1 and 3 pounds of resource 1 to make each unit of X2. There are only 150 pounds of resource 1 available. Which of the following constraints reflects the relationship between X1, X2 and resource 1?
A) 4 X1 + 3 X2 ≥ 150
B) 4 X1 + 3 X2 ≤ 150
C) 4 X1 + 3 X2 = 150
D) 4 X1 ≤ 150
A) 4 X1 + 3 X2 ≥ 150
B) 4 X1 + 3 X2 ≤ 150
C) 4 X1 + 3 X2 = 150
D) 4 X1 ≤ 150

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
55
A mathematical programming application employed by a shipping company is most likely
A) a product mix problem.
B) a manufacturing problem.
C) a routing and logistics problem.
D) a financial planning problem.
A) a product mix problem.
B) a manufacturing problem.
C) a routing and logistics problem.
D) a financial planning problem.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
56
The following linear programming problem has been written to plan the production of two products. The company wants to maximize its profits. X1 = number of product 1 produced in each batch
X2 = number of product 2 produced in each batch How many units of resource one (the first constraint) are used if the company produces 10 units of product 1 and 5 units of product 2?
How many units of resource one (the first constraint) are used if the company produces 10 units of product 1 and 5 units of product 2?
A) 45
B) 15
C) 55
D) 50
X2 = number of product 2 produced in each batch
 How many units of resource one (the first constraint) are used if the company produces 10 units of product 1 and 5 units of product 2?
How many units of resource one (the first constraint) are used if the company produces 10 units of product 1 and 5 units of product 2?A) 45
B) 15
C) 55
D) 50

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
57
The constraint for resource 1 is 5 X1 + 4 X2 ≥ 200. If X2 = 20, what it the minimum value for X1?
A) 20
B) 24
C) 40
D) 50
A) 20
B) 24
C) 40
D) 50

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
58
A common objective when manufacturing printed circuit boards is
A) maximizing the number of holes drilled.
B) maximizing the number of drill bit changes.
C) minimizing the number of holes drilled.
D) minimizing the total distance the drill bit must be moved.
A) maximizing the number of holes drilled.
B) maximizing the number of drill bit changes.
C) minimizing the number of holes drilled.
D) minimizing the total distance the drill bit must be moved.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
59
What most motivates a business to be concerned with efficient use of their resources?
A) Resources are limited and valuable.
B) Efficient resource use increases business costs.
C) Efficient resources use means more free time.
D) Inefficient resource use means hiring more workers.
A) Resources are limited and valuable.
B) Efficient resource use increases business costs.
C) Efficient resources use means more free time.
D) Inefficient resource use means hiring more workers.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
60
The following linear programming problem has been written to plan the production of two products. The company wants to maximize its profits. X1 = number of product 1 produced in each batch
X2 = number of product 2 produced in each batch How many units of resource 1 are consumed by each unit of product 1 produced?
How many units of resource 1 are consumed by each unit of product 1 produced?
A) 1
B) 2
C) 3
D) 5
X2 = number of product 2 produced in each batch
 How many units of resource 1 are consumed by each unit of product 1 produced?
How many units of resource 1 are consumed by each unit of product 1 produced?A) 1
B) 2
C) 3
D) 5

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the following LP problem graphically using level curves. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
62
Bob and Dora Sweet wish to start investing $1,000 each month. The Sweets are looking at five investment plans and wish to maximize their expected return each month. Assume interest rates remain fixed and once their investment plan is selected they do not change their mind. The investment plans offered are:  Since Optima and National are riskier, the Sweets want a limit of 30% per month of their total investments placed in these two investments. Since Safeway and Fidelity are low risk, they want at least 40% of their investment total placed in these investments.
Since Optima and National are riskier, the Sweets want a limit of 30% per month of their total investments placed in these two investments. Since Safeway and Fidelity are low risk, they want at least 40% of their investment total placed in these investments.
Formulate the LP model for this problem.
 Since Optima and National are riskier, the Sweets want a limit of 30% per month of their total investments placed in these two investments. Since Safeway and Fidelity are low risk, they want at least 40% of their investment total placed in these investments.
Since Optima and National are riskier, the Sweets want a limit of 30% per month of their total investments placed in these two investments. Since Safeway and Fidelity are low risk, they want at least 40% of their investment total placed in these investments.Formulate the LP model for this problem.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the following LP problem graphically using level curves. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
64
Retail companies try to find
A) the least costly method of transferring goods from warehouses to stores.
B) the most costly method of transferring goods from warehouses to stores.
C) the largest number of goods to transfer from warehouses to stores.
D) the least profitable method of transferring goods from warehouses to stores.
A) the least costly method of transferring goods from warehouses to stores.
B) the most costly method of transferring goods from warehouses to stores.
C) the largest number of goods to transfer from warehouses to stores.
D) the least profitable method of transferring goods from warehouses to stores.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
65
The following linear programming problem has been written to plan the production of two products. The company wants to maximize its profits. X1 = number of product 1 produced in each batch
X2 = number of product 2 produced in each batch How many units of resource two (the second constraint) are unutilized if the company produces 10 units of product 1 and 5 units of product 2?
How many units of resource two (the second constraint) are unutilized if the company produces 10 units of product 1 and 5 units of product 2?
A) 110
B) 150
C) 155
D) 100
X2 = number of product 2 produced in each batch
 How many units of resource two (the second constraint) are unutilized if the company produces 10 units of product 1 and 5 units of product 2?
How many units of resource two (the second constraint) are unutilized if the company produces 10 units of product 1 and 5 units of product 2?A) 110
B) 150
C) 155
D) 100

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the following LP problem graphically using level curves. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
67
The constraint for resource 1 is 5 X1 + 4 X2 ≤ 200. If X1 = 20 and X2 = 5, how much of resource 1 is unused?
A) 0
B) 80
C) 100
D) 200
A) 0
B) 80
C) 100
D) 200

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the following LP problem graphically by enumerating the corner points. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the following LP problem graphically by enumerating the corner points. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the following LP problem graphically using level curves. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
71
Which of the following fields of business analytics finds the optimal method of using resources to achieve the objectives of a business?
A) Simulation
B) Regression
C) Mathematical programming
D) Discriminant analysis
A) Simulation
B) Regression
C) Mathematical programming
D) Discriminant analysis

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the following LP problem graphically by enumerating the corner points. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
73
Project 2.1
Joey Koons runs a small custom computer parts company. As a sideline he offers customized and pre-built computer system packages. In preparation for the upcoming school year, he has decided to offer two custom computer packages tailored for what he believes are current student needs. System A provides a strong computing capability at a reasonable cost while System B provides a much more powerful computing capability, but at a higher cost. Joey has a fairly robust parts inventory but is concerned about his stock of those components that are common to each proposed system. A portion of his inventory, the item cost, and inventory level is provided in the table below.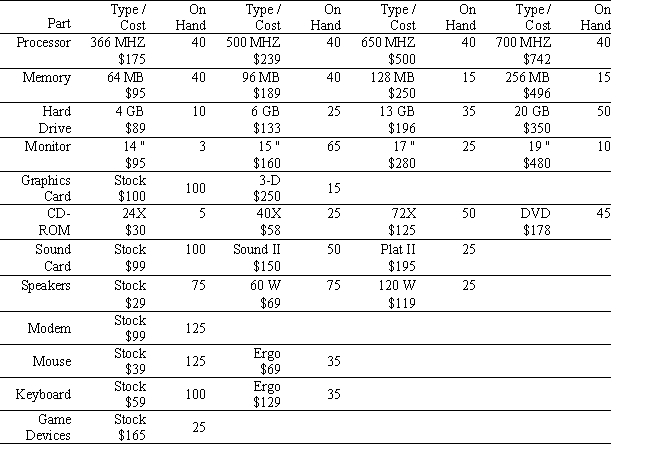 The requirements for each system are provided in the following table:
The requirements for each system are provided in the following table: 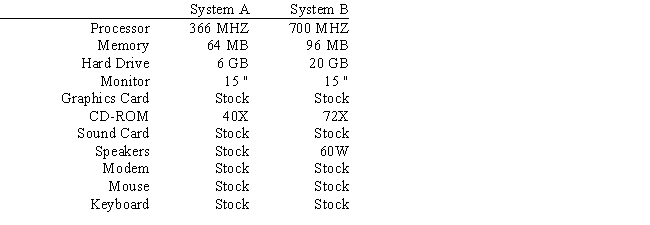 Each system requires assembly, testing and packaging. The requirements per system built and resources available are summarized in the table below.
Each system requires assembly, testing and packaging. The requirements per system built and resources available are summarized in the table below.  Joey is uncertain about product demand. In the past he has put together similar types of computer packages but his sales results vary. As a result is unwilling to commit all his in-house labor force to building the computer packages. He is confident he can sell all he can build and is not overly concerned with lost sales due to stock-outs. Based on his market survey, he has completed his advertising flyer and will offer System A for $ 1250 and will offer system B for $ 2325. Joey now needs to let his workers know how many of each system to build and he wants that mix to maximize his profits.
Joey is uncertain about product demand. In the past he has put together similar types of computer packages but his sales results vary. As a result is unwilling to commit all his in-house labor force to building the computer packages. He is confident he can sell all he can build and is not overly concerned with lost sales due to stock-outs. Based on his market survey, he has completed his advertising flyer and will offer System A for $ 1250 and will offer system B for $ 2325. Joey now needs to let his workers know how many of each system to build and he wants that mix to maximize his profits.
Formulate an LP for Dave's problem. Solve the model using the graphical method. What is Dave's preferred product mix? What profit does Dave expect to make from this product mix?
Joey Koons runs a small custom computer parts company. As a sideline he offers customized and pre-built computer system packages. In preparation for the upcoming school year, he has decided to offer two custom computer packages tailored for what he believes are current student needs. System A provides a strong computing capability at a reasonable cost while System B provides a much more powerful computing capability, but at a higher cost. Joey has a fairly robust parts inventory but is concerned about his stock of those components that are common to each proposed system. A portion of his inventory, the item cost, and inventory level is provided in the table below.
 The requirements for each system are provided in the following table:
The requirements for each system are provided in the following table:  Each system requires assembly, testing and packaging. The requirements per system built and resources available are summarized in the table below.
Each system requires assembly, testing and packaging. The requirements per system built and resources available are summarized in the table below.  Joey is uncertain about product demand. In the past he has put together similar types of computer packages but his sales results vary. As a result is unwilling to commit all his in-house labor force to building the computer packages. He is confident he can sell all he can build and is not overly concerned with lost sales due to stock-outs. Based on his market survey, he has completed his advertising flyer and will offer System A for $ 1250 and will offer system B for $ 2325. Joey now needs to let his workers know how many of each system to build and he wants that mix to maximize his profits.
Joey is uncertain about product demand. In the past he has put together similar types of computer packages but his sales results vary. As a result is unwilling to commit all his in-house labor force to building the computer packages. He is confident he can sell all he can build and is not overly concerned with lost sales due to stock-outs. Based on his market survey, he has completed his advertising flyer and will offer System A for $ 1250 and will offer system B for $ 2325. Joey now needs to let his workers know how many of each system to build and he wants that mix to maximize his profits.Formulate an LP for Dave's problem. Solve the model using the graphical method. What is Dave's preferred product mix? What profit does Dave expect to make from this product mix?

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the following LP problem graphically by enumerating the corner points. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the following LP problem graphically using level curves. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
76
Some resources (i.e. meat and dairy products, pharmaceuticals, a can of paint) are perishable. This means that once a package (e.g. a can or a bag) is open the content should be used in its entirety. Which of the following constraints reflects this fact?
A) f(X1, X2, X3, X4) ≤ b1
B) f(X1, X2, X3, X4) ≥ b1
C) f(X1, X2, X3, X4) = b1
D) f(X1, X2, X3, X4) ≠ b1
A) f(X1, X2, X3, X4) ≤ b1
B) f(X1, X2, X3, X4) ≥ b1
C) f(X1, X2, X3, X4) = b1
D) f(X1, X2, X3, X4) ≠ b1

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck


