Deck 10: Statistical Inference Concerning Two Populations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/124
Play
Full screen (f)
Deck 10: Statistical Inference Concerning Two Populations
1
The margin of error in the confidence interval for the difference 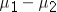 equals the standard error
equals the standard error 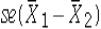 multiplied by either
multiplied by either 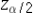 or
or 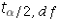 depending on whether or not the population variances are known.
depending on whether or not the population variances are known.
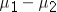 equals the standard error
equals the standard error 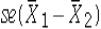 multiplied by either
multiplied by either 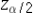 or
or 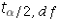 depending on whether or not the population variances are known.
depending on whether or not the population variances are known.True
2
A common case of dependent sampling is usually referred to as __________ sampling.
matched-pairs
3
The test statistic for testing the difference between two means are valid only when the sampling distribution of 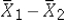 is_________ .
is_________ .
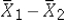 is_________ .
is_________ .normal
4
We use the difference between the sample proportions 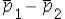 as the point estimator of the difference between two population proportions
as the point estimator of the difference between two population proportions 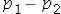 .
.
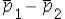 as the point estimator of the difference between two population proportions
as the point estimator of the difference between two population proportions 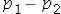 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
5
A left-tailed test determines whether μ1is _____ then μ2.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
6
Statistical inference about the differences between two population means based on _________ random samples.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
7
In the case when 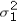 and
and 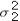 are unknown and can be assumed equal,we can calculate a pooled estimate of the population variance.
are unknown and can be assumed equal,we can calculate a pooled estimate of the population variance.
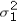 and
and 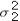 are unknown and can be assumed equal,we can calculate a pooled estimate of the population variance.
are unknown and can be assumed equal,we can calculate a pooled estimate of the population variance.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
8
The same formulas are used to compute test statistic when the hypothesized difference between population proportions is zero or not.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
9
When constructing a confidence interval for the mean difference 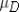 ,we follow the same general format of point estimate ± _________ .
,we follow the same general format of point estimate ± _________ .
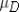 ,we follow the same general format of point estimate ± _________ .
,we follow the same general format of point estimate ± _________ .
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
10
We always deal with matched-pairs sampling if two samples have the same number of observations.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
11
The difference between the two sample means 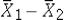 is an interval estimator of the difference between two population means
is an interval estimator of the difference between two population means 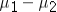 .
.
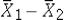 is an interval estimator of the difference between two population means
is an interval estimator of the difference between two population means 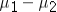 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
12
We convert the estimate  into the corresponding value of the z or t test statistic by dividing the difference between
into the corresponding value of the z or t test statistic by dividing the difference between  and the hypothesized difference
and the hypothesized difference 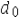 by the standard error of the estimator
by the standard error of the estimator 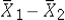 .
.
 into the corresponding value of the z or t test statistic by dividing the difference between
into the corresponding value of the z or t test statistic by dividing the difference between  and the hypothesized difference
and the hypothesized difference 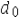 by the standard error of the estimator
by the standard error of the estimator 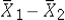 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
13
Two random samples are considered independent if the observations in the first sample are different from the observations of the second sample.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
14
There is only one type of matched-pairs sampling.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
15
For a statistical inference regarding 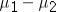 ,it is imperative that the sampling distribution of
,it is imperative that the sampling distribution of 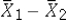 is normally distributed.
is normally distributed.
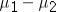 ,it is imperative that the sampling distribution of
,it is imperative that the sampling distribution of 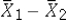 is normally distributed.
is normally distributed.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
16
The statistical inference concerning the difference between two population proportions is used for qualitative data.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
17
The t statistic is used to estimate the difference between two population proportions.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
18
The confidence interval for the difference 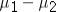 is based on the same approach used in the case of one sample: Point Estimate ± Standard Error.
is based on the same approach used in the case of one sample: Point Estimate ± Standard Error.
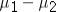 is based on the same approach used in the case of one sample: Point Estimate ± Standard Error.
is based on the same approach used in the case of one sample: Point Estimate ± Standard Error.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
19
If the underlying populations cannot be assumed to be normal,then by the central limit theorem,the sampling distribution of 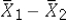 is approximately normal only if the sum of the sample observations is sufficiently large-that is,when
is approximately normal only if the sum of the sample observations is sufficiently large-that is,when 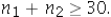
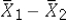 is approximately normal only if the sum of the sample observations is sufficiently large-that is,when
is approximately normal only if the sum of the sample observations is sufficiently large-that is,when 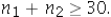

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
20
The hypothesis test H0: p1- p2≤ d0;HA: p1- p2> d0 is a left-tailed test.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
21
A demographer wants to measure life expectancy in countries 1 and 2.Let 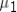 and
and 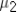 denote the mean life expectancy in countries 1 and 2,respectively.Specify the hypothesis to determine if life expectancy in country 1 is more than 10 years lower than in country 2.
denote the mean life expectancy in countries 1 and 2,respectively.Specify the hypothesis to determine if life expectancy in country 1 is more than 10 years lower than in country 2.
A) H0: µ1- µ2 ≤ 10,HA: µ1- µ2 > 10
B) H0: µ1- µ2 ≥ 10,HA: µ1- µ2 < 10
C) H0: µ1- µ2 ≤ -10,HA: µ1- µ2 > −10
D) H0: µ1- µ2 ≥ -10,HA: µ1- µ2 < −10
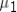 and
and 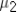 denote the mean life expectancy in countries 1 and 2,respectively.Specify the hypothesis to determine if life expectancy in country 1 is more than 10 years lower than in country 2.
denote the mean life expectancy in countries 1 and 2,respectively.Specify the hypothesis to determine if life expectancy in country 1 is more than 10 years lower than in country 2.A) H0: µ1- µ2 ≤ 10,HA: µ1- µ2 > 10
B) H0: µ1- µ2 ≥ 10,HA: µ1- µ2 < 10
C) H0: µ1- µ2 ≤ -10,HA: µ1- µ2 > −10
D) H0: µ1- µ2 ≥ -10,HA: µ1- µ2 < −10

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
22
In the test for comparing two population means when population variances are unknown and unequal,a student calculates the degrees of freedom using the proper formula as 34.7.How many degrees of freedom should the student assume to find the p-value of the test?
A) 34
B) 34.7
C) 35
D) None of these choices is correct.
A) 34
B) 34.7
C) 35
D) None of these choices is correct.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
23
To use Excel for solving hypothesis tests for the mean difference you should choose: Data > __________ > t-Test: Paired Two Sample for Means options.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
24
When testing the difference between two population means under independent sampling,we use the z distribution if _________ .
A) the population variances are known
B) the population variances are unknown,but assumed to be equal
C) the population variances are unknown and cannot be assumed equal
D) Both the population variances are known and the population variances are unknown,but assumed to be equal
A) the population variances are known
B) the population variances are unknown,but assumed to be equal
C) the population variances are unknown and cannot be assumed equal
D) Both the population variances are known and the population variances are unknown,but assumed to be equal

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
25
Assume the competing hypotheses take the following form H0: µ1-µ2 = 0,HA: µ1-µ2 ≠ 0,where µ1 is the population mean for population 1 and µ2 is the population mean for population 2.Also assume that the populations are normally distributed with known variances and we use independent sampling.Which of the following expressions is appropriate test statistic?
A)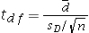
B)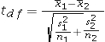
C)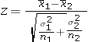
D)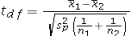
A)
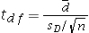
B)
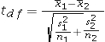
C)
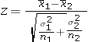
D)
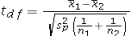

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
26
What formula is used to calculate the degrees of freedom for the t test for comparing two population means when the population variances are unknown and unequal?
A) df = n - 1
B) df = n1 + n2 - 2
C) df = n1+ n2-1
D)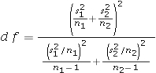
A) df = n - 1
B) df = n1 + n2 - 2
C) df = n1+ n2-1
D)
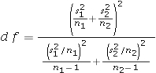

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
27
When comparing two population means,their hypothesized difference _________ .
A) must be negative
B) must be positive
C) must be zero
D) may assume any value
A) must be negative
B) must be positive
C) must be zero
D) may assume any value

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
28
The choice of an appropriate test for comparing two population means depends on whether we deal with _________ .
A) qualitative or quantitative data
B) independent or matched-pairs sampling
C) the equality or lack of equality of population variances
D) All of these choices are correct
A) qualitative or quantitative data
B) independent or matched-pairs sampling
C) the equality or lack of equality of population variances
D) All of these choices are correct

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
29
Assume the competing hypotheses take the following form: H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0,where µ1 is the population mean for population 1 and µ2 is the population mean for population 2.Also assume that the populations are normally distributed and we use independent sampling.The population variances are not known and cannot be assumed equal.Which of the following expressions is appropriate test statistic?
A)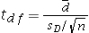
B)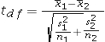
C)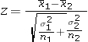
D)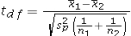
A)
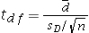
B)
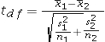
C)
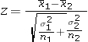
D)
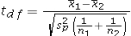

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
30
We estimate the unknown standard deviation for 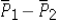 by the _________ .
by the _________ .
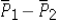 by the _________ .
by the _________ .
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
31
If the sampling distribution of  cannot be assumed normal,we _________ .
cannot be assumed normal,we _________ .
A) are unable to compute a confidence interval
B) are still able to use the z distribution to compute a confidence interval
C) must use the tdf distribution with n1 + n2 - 2 degrees of freedom to compute a confidence interval
D) must use the tdf distribution and calculate the degrees of freedom using n1,n2,s1,ands2 to compute a confidence interval
 cannot be assumed normal,we _________ .
cannot be assumed normal,we _________ .A) are unable to compute a confidence interval
B) are still able to use the z distribution to compute a confidence interval
C) must use the tdf distribution with n1 + n2 - 2 degrees of freedom to compute a confidence interval
D) must use the tdf distribution and calculate the degrees of freedom using n1,n2,s1,ands2 to compute a confidence interval

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the following is not a restriction for comparing two population means?
A) A normally distributed sampling distribution of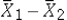
B) The equality of the sample sizes
C) Both of these choices are correct.
D) Neither of these choices are correct.
A) A normally distributed sampling distribution of
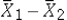
B) The equality of the sample sizes
C) Both of these choices are correct.
D) Neither of these choices are correct.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
33
Assume the competing hypotheses take the following form: H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0,where µ1 is the population mean for population 1 and µ2 is the population mean for population 2.Also assume that the populations are normally distributed and that the observations in the two samples are independent.The population variances are not known but are assumed equal.Which of the following expressions is appropriate test statistic?
A)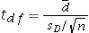
B)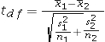
C)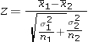
D)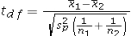
A)
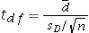
B)
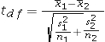
C)
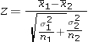
D)
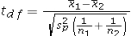

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
34
If the hypothesized difference d0 is ______,then the value of the test statistic is computed as 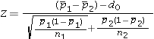
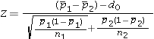

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
35
What type of test for population means should be performed when examining a situation in which employees are first tested,then trained,and finally retested?
A) A z test under independent sampling with known population variances.
B) A t test under independent sampling with unknown but equal population variances.
C) A t test under dependent sampling.
D) A t test under independent sampling with unknown and unequal population variances.
A) A z test under independent sampling with known population variances.
B) A t test under independent sampling with unknown but equal population variances.
C) A t test under dependent sampling.
D) A t test under independent sampling with unknown and unequal population variances.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following pairs of hypotheses are used to test if the mean of the first population is smaller than the mean of the second population,using independent random sampling?
A) H0: µD ≤0,HA: µD >0
B) H0: µD ≥0,HA: µD <0
C) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
D) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
A) H0: µD ≤0,HA: µD >0
B) H0: µD ≥0,HA: µD <0
C) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
D) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
37
When calculating the standard error of 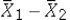 ,under what assumption do you pool the sample variances
,under what assumption do you pool the sample variances 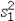 and
and 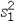 ?
?
A) Known population variances.
B) Unknown population variances that are assumed equal.
C) Unknown population variances that are assumed unequal.
D) All of these choices are correct.
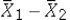 ,under what assumption do you pool the sample variances
,under what assumption do you pool the sample variances 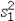 and
and 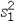 ?
?A) Known population variances.
B) Unknown population variances that are assumed equal.
C) Unknown population variances that are assumed unequal.
D) All of these choices are correct.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
38
If the underlying populations cannot be assumed to be normal,then by the central limit theorem,the sampling distribution of 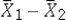 is approximately normal only if both sample sizes are sufficiently large-that is,when _________ .
is approximately normal only if both sample sizes are sufficiently large-that is,when _________ .
A) n1 + n2 = 30
B) n1 + n2 ≥ 30
C) n1 = 30 and n2 = 30
D) n1 ≥ 30 and n2 ≥ 30
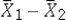 is approximately normal only if both sample sizes are sufficiently large-that is,when _________ .
is approximately normal only if both sample sizes are sufficiently large-that is,when _________ .A) n1 + n2 = 30
B) n1 + n2 ≥ 30
C) n1 = 30 and n2 = 30
D) n1 ≥ 30 and n2 ≥ 30

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose you want to perform a test to compare the mean GPA of all freshmen with the mean GPA of all sophomores in a college? What type of sampling is required for this test?
A) Independent sampling with qualitative data
B) Independent sampling with quantitative data
C) Matched-pairs sampling with qualitative data
D) Matched-pairs sampling with quantitative data
A) Independent sampling with qualitative data
B) Independent sampling with quantitative data
C) Matched-pairs sampling with qualitative data
D) Matched-pairs sampling with quantitative data

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
40
Two or more random samples are considered independent if _________ .
A) the process that generates one sample is the same as the process that generates the other sample
B) the process that generates one sample partially overlaps the process that generates the other sample
C) the process that generates one sample completely overlaps the process that generates the other sample
D) the process that generates one sample is completely separate from the process that generates the other sample
A) the process that generates one sample is the same as the process that generates the other sample
B) the process that generates one sample partially overlaps the process that generates the other sample
C) the process that generates one sample completely overlaps the process that generates the other sample
D) the process that generates one sample is completely separate from the process that generates the other sample

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
41
You would like to determine if there is a higher incidence of smoking among women than among men in a neighborhood.Let men and women be represented by populations 1 and 2,respectively.Which of the following hypotheses is relevant to this claim?
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: p1- p2 ≤ 0,HA: p1- p2 > 0
D) H0: p1- p2 ≥ 0,HA: p1- p2 < 0
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: p1- p2 ≤ 0,HA: p1- p2 > 0
D) H0: p1- p2 ≥ 0,HA: p1- p2 < 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
42
A farmer uses a lot of fertilizer to grow his crops.The farmer's manager thinks fertilizer products from distributor A contain more of the nitrogen that his plants need than distributor B's fertilizer does.He takes two independent samples of four batches of fertilizer from each distributor and measures the amount of nitrogen in each batch.Fertilizer from distributor A contained 23 pounds per batch and fertilizer from distributor B contained 18 pounds per batch.Suppose the population standard deviation for distributor A and distributor B is four pounds per batch and five pounds per batch,respectively.Assume the distribution of nitrogen in fertilizer is normally distributed.Let µ1and µ2 represent the average amount of nitrogen per batch for fertilizer's A and B,respectively.Which of the following is the correct value of the test statistic?
A) t6 = −1.5617
B) t6 = 1.5617
C) z = −1.5617
D) z = 1.5617
A) t6 = −1.5617
B) t6 = 1.5617
C) z = −1.5617
D) z = 1.5617

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
43
A restaurant chain has two locations in a medium-sized town and,believing that it has oversaturated the market for its food,is considering closing one of the restaurants.The manager of the restaurant with a downtown location claims that his restaurant generates more revenue than the sister restaurant by the freeway.The CEO of this company,wishing to test this claim,randomly selects 36 monthly revenue totals for each restaurant.The revenue data from the downtown restaurant have a mean of $360,000 and a standard deviation of $50,000,while the data from the restaurant by the freeway have a mean of $340,000 and a standard deviation of $40,000.Assume there is no reason to believe the population standard deviations are equal,and let μ1 and μ2 denote the mean monthly revenue of the downtown restaurant and the restaurant by the freeway,respectively.At the 5% significance level,does the evidence support the manager's claim?
A) No,because the test statistic value is less than the critical value.
B) Yes,because the test statistic value is less than the critical value.
C) No,because the test statistic value is greater than the critical value.
D) Yes,because the test statistic value is greater than the critical value.
A) No,because the test statistic value is less than the critical value.
B) Yes,because the test statistic value is less than the critical value.
C) No,because the test statistic value is greater than the critical value.
D) Yes,because the test statistic value is greater than the critical value.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
44
A particular personal trainer works primarily with track and field athletes.She believes that her clients run faster after going through her program for six weeks.How might she test that claim?
A) A hypothesis test for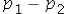 .
.
B) A hypothesis test for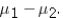
C) A matched-pairs hypothesis test for μD.
D) We are unable to conduct a hypothesis test because the samples would not be independent.
A) A hypothesis test for
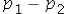 .
.B) A hypothesis test for
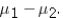
C) A matched-pairs hypothesis test for μD.
D) We are unable to conduct a hypothesis test because the samples would not be independent.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
45
What type of data is required to compare prices of the same textbooks sold by two different vendors?
A) Dependent random samples with qualitative data.
B) Dependent random samples with quantitative data.
C) Independent random samples with qualitative data.
D) Independent random samples with quantitative data.
A) Dependent random samples with qualitative data.
B) Dependent random samples with quantitative data.
C) Independent random samples with qualitative data.
D) Independent random samples with quantitative data.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
46
A particular bank has two loan modification programs for distressed borrowers: Home Affordable Modification Program (HAMP)modifications,where the federal government pays the bank $1,000 for each successful modification,and non-HAMP modifications,where the bank does not receive a bonus from the federal government.To qualify for a HAMP modification,borrowers must meet a set of financial suitability criteria.What type of hypothesis test should we use to test whether borrowers from this particular bank who receive HAMP modifications are more likely to re-default than those who receive non-HAMP modifications?
A) A hypothesis test for p1- p2.
B) A hypothesis test for µ1- µ2.
C) A matched-pairs hypothesis test.
D) We are unable to conduct a hypothesis test because independent random samples of each group could not be collected.
A) A hypothesis test for p1- p2.
B) A hypothesis test for µ1- µ2.
C) A matched-pairs hypothesis test.
D) We are unable to conduct a hypothesis test because independent random samples of each group could not be collected.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
47
A restaurant chain has two locations in a medium-sized town and,believing that it has oversaturated the market for its food,is considering closing one of the restaurants.The manager of the restaurant with a downtown location claims that his restaurant generates more revenue than the sister restaurant by the freeway.The CEO of this company,wishing to test this claim,randomly selects 36 monthly revenue totals for each restaurant.The revenue data from the downtown restaurant have a mean of $360,000 and a standard deviation of $50,000,while the data from the restaurant by the freeway have a mean of $340,000 and a standard deviation of $40,000.Assume there is no reason to believe the population standard deviations are equal,and let μ1 and μ2 denote the mean monthly revenue of the downtown restaurant and the restaurant by the freeway,respectively.Which of the following is the appropriate critical value(s)to test the manager's claim at the 5% significance level?
A) 1.645
B) 1.668
C) 1.960
D) 1.997
A) 1.645
B) 1.668
C) 1.960
D) 1.997

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
48
Calcium is an essential nutrient for strong bones and for controlling blood pressure and heart beat.Because most of the body's calcium is stored in bones and teeth,the body withdraws the calcium it needs from the bones.Over time,if more calcium is taken out of the bones than is put in,the result may be thin,weak bones.This is especially important for women who are often recommended a calcium supplement.A consumer group activist assumes that calcium content in two popular supplements are normally distributed with the same unknown population variance,and uses the following information obtained under independent sampling: ![<strong>Calcium is an essential nutrient for strong bones and for controlling blood pressure and heart beat.Because most of the body's calcium is stored in bones and teeth,the body withdraws the calcium it needs from the bones.Over time,if more calcium is taken out of the bones than is put in,the result may be thin,weak bones.This is especially important for women who are often recommended a calcium supplement.A consumer group activist assumes that calcium content in two popular supplements are normally distributed with the same unknown population variance,and uses the following information obtained under independent sampling: Let μ<sub>1</sub> and μ<sub>2</sub> denote the corresponding population means.Construct a 95% confidence interval for the difference μ<sub>1</sub> - μ<sub>2</sub>.</strong> A) [-30.9386,1.0614] B) [-31.5886,-0.4114] C) [-33.8007,1.8007] D) [-34.8012,2.8012]](https://storage.examlex.com/TB4266/11eab0ce_3108_e76b_a083_871f13129f2b_TB4266_00.jpg) Let μ1 and μ2 denote the corresponding population means.Construct a 95% confidence interval for the difference μ1 - μ2.
Let μ1 and μ2 denote the corresponding population means.Construct a 95% confidence interval for the difference μ1 - μ2.
A) [-30.9386,1.0614]
B) [-31.5886,-0.4114]
C) [-33.8007,1.8007]
D) [-34.8012,2.8012]
![<strong>Calcium is an essential nutrient for strong bones and for controlling blood pressure and heart beat.Because most of the body's calcium is stored in bones and teeth,the body withdraws the calcium it needs from the bones.Over time,if more calcium is taken out of the bones than is put in,the result may be thin,weak bones.This is especially important for women who are often recommended a calcium supplement.A consumer group activist assumes that calcium content in two popular supplements are normally distributed with the same unknown population variance,and uses the following information obtained under independent sampling: Let μ<sub>1</sub> and μ<sub>2</sub> denote the corresponding population means.Construct a 95% confidence interval for the difference μ<sub>1</sub> - μ<sub>2</sub>.</strong> A) [-30.9386,1.0614] B) [-31.5886,-0.4114] C) [-33.8007,1.8007] D) [-34.8012,2.8012]](https://storage.examlex.com/TB4266/11eab0ce_3108_e76b_a083_871f13129f2b_TB4266_00.jpg) Let μ1 and μ2 denote the corresponding population means.Construct a 95% confidence interval for the difference μ1 - μ2.
Let μ1 and μ2 denote the corresponding population means.Construct a 95% confidence interval for the difference μ1 - μ2.A) [-30.9386,1.0614]
B) [-31.5886,-0.4114]
C) [-33.8007,1.8007]
D) [-34.8012,2.8012]

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
49
You would like to determine if there is a higher incidence of smoking among women than among men in a neighborhood.Let women and men be represented by populations 1 and 2,respectively.Which of the following hypotheses is relevant to this claim?
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: p1- p2 ≤ 0,HA: p1- p2 > 0
D) H0: p1- p2 ≥ 0,HA: p1- p2 < 0
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: p1- p2 ≤ 0,HA: p1- p2 > 0
D) H0: p1- p2 ≥ 0,HA: p1- p2 < 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
50
When the hypothesized difference of the population proportions is equal to 0,we _________ .
A) use a matched-pairs approach
B) are able to estimate the standard error of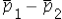 using the pooled
using the pooled 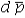
C) can use the confidence interval to implement the test if the difference of the population proportions is equal to 0
D) Both estimate the standard error of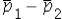
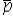
A) use a matched-pairs approach
B) are able to estimate the standard error of
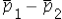 using the pooled
using the pooled 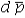
C) can use the confidence interval to implement the test if the difference of the population proportions is equal to 0
D) Both estimate the standard error of
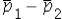
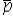

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
51
A particular bank has two loan modification programs for distressed borrowers: Home Affordable Modification Program (HAMP)modifications,where the federal government pays the bank $1,000 for each successful modification,and non-HAMP modifications,where the bank does not receive a bonus from the federal government.To qualify for a HAMP modification,borrowers must meet a set of financial suitability criteria.Define the null and alternative hypotheses to test whether borrowers who receive HAMP modifications default less than borrowers who receive non-HAMP modifications.Let p1 and p2 represent the proportion of borrowers who received HAMP and non-HAMP modifications that did not re-default,respectively.
A) H0: p1- p2 ≤ 0,HA: p1- p2 > 0
B) H0: p1- p2 ≥ 0,HA: p1- p2 < 0
C) H0: p1- p2 = 0,HA: p1- p2 ≠ 0
D) H0: p1- p2 > 0,HA: p1- p2 ≤ 0
A) H0: p1- p2 ≤ 0,HA: p1- p2 > 0
B) H0: p1- p2 ≥ 0,HA: p1- p2 < 0
C) H0: p1- p2 = 0,HA: p1- p2 ≠ 0
D) H0: p1- p2 > 0,HA: p1- p2 ≤ 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
52
What type of data should be collected when examining a situation in which two candidates running in different elections are being compared in their likelihood of winning their elections?
A) Matched-pairs sampling with qualitative data.
B) Matched-pairs sampling with quantitative data.
C) Independent sampling with qualitative data.
D) Independent sampling with quantitative data.
A) Matched-pairs sampling with qualitative data.
B) Matched-pairs sampling with quantitative data.
C) Independent sampling with qualitative data.
D) Independent sampling with quantitative data.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
53
A restaurant chain has two locations in a medium-sized town and,believing that it has oversaturated the market for its food,is considering closing one of the restaurants.The manager of the restaurant with a downtown location claims that his restaurant generates more revenue than the sister restaurant by the freeway.The CEO of this company,wishing to test this claim,randomly selects 36 monthly revenue totals for each restaurant.The revenue data from the downtown restaurant have a mean of $360,000 and a standard deviation of $50,000,while the data from the restaurant by the freeway have a mean of $340,000 and a standard deviation of $40,000.Assume there is no reason to believe the population standard deviations are equal,and let μ1 and μ2 denote the mean monthly revenue of the downtown restaurant and the restaurant by the freeway,respectively.Which of the following is the correct value of the test statistic to analyze the claim?
A) t66 = 1.848
B) t67 = 1.848
C) t66 = 1.874
D) t67 = 1.874
A) t66 = 1.848
B) t67 = 1.848
C) t66 = 1.874
D) t67 = 1.874

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
54
Calcium is an essential nutrient for strong bones and for controlling blood pressure and heart beat.Because most of the body's calcium is stored in bones and teeth,the body withdraws the calcium it needs from the bones.Over time,if more calcium is taken out of the bones than is put in,the result may be thin,weak bones.This is especially important for women who are often recommended a calcium supplement.A consumer group activist assumes that calcium content in two popular supplements are normally distributed with the same unknown population variance,and uses the following information obtained under independent sampling: 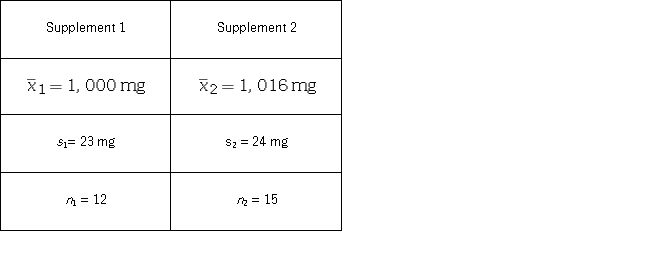 Let μ1 and μ2 denote the corresponding population means.Can we conclude that the average calcium content of the two supplements differs at the 95% confidence level?
Let μ1 and μ2 denote the corresponding population means.Can we conclude that the average calcium content of the two supplements differs at the 95% confidence level?
A) No,because the 95% confidence interval contains the hypothesized value of zero.
B) Yes,because the 95% confidence interval contains the hypothesized value of zero.
C) No,because the 95% confidence interval does not contain the hypothesized value of zero.
D) Yes,because the 95% confidence interval does not contain the hypothesized value of zero.
 Let μ1 and μ2 denote the corresponding population means.Can we conclude that the average calcium content of the two supplements differs at the 95% confidence level?
Let μ1 and μ2 denote the corresponding population means.Can we conclude that the average calcium content of the two supplements differs at the 95% confidence level?A) No,because the 95% confidence interval contains the hypothesized value of zero.
B) Yes,because the 95% confidence interval contains the hypothesized value of zero.
C) No,because the 95% confidence interval does not contain the hypothesized value of zero.
D) Yes,because the 95% confidence interval does not contain the hypothesized value of zero.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
55
Which of the following is appropriate to conduct a hypothesis test for the difference between two population proportions under independent sampling.
A) In every case.
B) Only if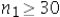 and
and 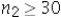 .
.
C) Only if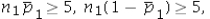
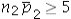 ,and
,and 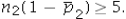
D) Only if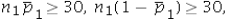
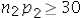
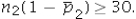
A) In every case.
B) Only if
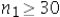 and
and 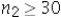 .
.C) Only if
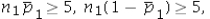
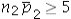 ,and
,and 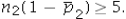
D) Only if
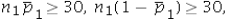

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
56
A 7,000-seat theater is interested in determining whether there is a difference in attendance between shows on Tuesday evening and those on Wednesday evening.Two independent samples of 25 weeks are collected for Tuesday and Wednesday.The mean attendance on Tuesday evening is calculated as 5,500,while the mean attendance on Wednesday evening is calculated as 5,850.The known population standard deviation for attendance on Tuesday evening is 550 and the known population standard deviation for attendance on Wednesday evening is 445.Which of the following is the value of the appropriate test statistic?
A) z = -2.4736
B) z = 2.4736
C) tdf = -2.4736
D) tdf = 2.4736
A) z = -2.4736
B) z = 2.4736
C) tdf = -2.4736
D) tdf = 2.4736

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
57
A farmer uses a lot of fertilizer to grow his crops.The farmer's manager thinks fertilizer products from distributor A contain more of the nitrogen that his plants need than distributor B's fertilizer does.He takes two independent samples of four batches of fertilizer from each distributor and measures the amount of nitrogen in each batch.Fertilizer from distributor A contained 23 pounds per batch and fertilizer from distributor B contained 18 pounds per batch.Suppose the population standard deviation for distributor A and distributor B is four pounds per batch and five pounds per batch,respectively.Assume the distribution of nitrogen in fertilizer is normally distributed.Let µ1and µ2 represent the average amount of nitrogen per batch for fertilizer's A and B,respectively.Which of the following is an appropriate p-value?
A) 0.0592
B) 0.0847
C) 0.0896
D) 0.1184
A) 0.0592
B) 0.0847
C) 0.0896
D) 0.1184

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
58
A restaurant chain has two locations in a medium-sized town and,believing that it has oversaturated the market for its food,is considering closing one of the restaurants.The manager of the restaurant with a downtown location claims that his restaurant generates more revenue than the sister restaurant by the freeway.The CEO of this company,wishing to test this claim,randomly selects 36 monthly revenue totals for each restaurant.The revenue data from the downtown restaurant have a mean of $360,000 and a standard deviation of $50,000,while the data from the restaurant by the freeway have a mean of $340,000 and a standard deviation of $40,000.Assume there is no reason to believe the population standard deviations are equal,and let μ1 and μ2 denote the mean monthly revenue of the downtown restaurant and the restaurant by the freeway,respectively.Which of the following hypotheses should be used to test the manager's claim?
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0
D) H0: µ1- µ2 > 0,HA: µ1- µ2 ≤ 0
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0
D) H0: µ1- µ2 > 0,HA: µ1- µ2 ≤ 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
59
A 7,000-seat theater is interested in determining whether there is a difference in attendance between shows on Tuesday evening and those on Wednesday evening.Two independent samples of 25 weeks are collected for Tuesday and Wednesday.The mean attendance on Tuesday evening is calculated as 5,500,while the mean attendance on Wednesday evening is calculated as 5,850.The known population standard deviation for attendance on Tuesday evening is 550 and the known population standard deviation for attendance on Wednesday evening is 445.What are the appropriate hypotheses to determine whether there is a difference in attendance for shows on Tuesday evening and Wednesday evening? Use Tuesday attendance as population 1 mean μ1 and Wednesday attendance as population 2 mean μ2,or μD as the mean difference in matched-pairs sampling.
A) H0: µD ≥ 0,HA: µD <0
B) H0: µD = 0,HA: µD ≠ 0
C) H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0
D) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
A) H0: µD ≥ 0,HA: µD <0
B) H0: µD = 0,HA: µD ≠ 0
C) H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0
D) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
60
Which of the following set of hypotheses is used to test if the mean of the first population is smaller than the mean of the second population,using matched-paired sampling?
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: µD ≤0,HA: µD > 0
D) H0: µD ≥0,HA: µD < 0
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: µD ≤0,HA: µD > 0
D) H0: µD ≥0,HA: µD < 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
61
A tutor promises to improve GMAT scores of students by more than 50 points after three lessons.To see if this is true,the tutor takes a sample of 49 students' test scores after and before they received tutoring.The mean difference was 53 points better after tutoring,with a standard deviation of the difference equal to 12 points.Let µD denote the mean of the difference: score after tutoring minus score before tutoring.Which of the following hypotheses will determine if the students improved their test scores by more than 50 points after being tutored?
A) H0: µD ≤ 0,HA: µD > 0
B) H0: µD ≥ 0,HA: µD <0
C) H0: µD ≤ 50,HA: µD >50
D) H0: µD ≥ 50,HA: µD <50
A) H0: µD ≤ 0,HA: µD > 0
B) H0: µD ≥ 0,HA: µD <0
C) H0: µD ≤ 50,HA: µD >50
D) H0: µD ≥ 50,HA: µD <50

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
62
A university wants to compare out-of-state applicants' mean SAT math scores (μ1)to in-state applicants' mean SAT math scores (μ2).The university looks at 35 in-state applicants and 35 out-of-state applicants.The mean SAT math score for in-state applicants was 540,with a standard deviation of 20.The mean SAT math score for out-of-state applicants was 555,with a standard deviation of 25.It is reasonable to assume the corresponding population standard deviations are equal.At the 5% significance level,can the university conclude that the mean SAT math score for in-state students and out-of-state students differ?
A) No,because the confidence interval contains zero.
B) Yes,because the confidence interval contains zero.
C) No,because the confidence interval does not contain zero.
D) Yes,because the confidence interval does not contain zero.
A) No,because the confidence interval contains zero.
B) Yes,because the confidence interval contains zero.
C) No,because the confidence interval does not contain zero.
D) Yes,because the confidence interval does not contain zero.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
63
A bank is trying to determine which model of safe to install.The bank manager believes that each model is equally resistant to safe crackers but sets up a test to be sure.He hires nine safe experts to break into each of the models,timing each endeavor.The results (in seconds)are given next,paired by expert.Let D be the difference: Time to break Safe 1 minus Time to break Safe 2. 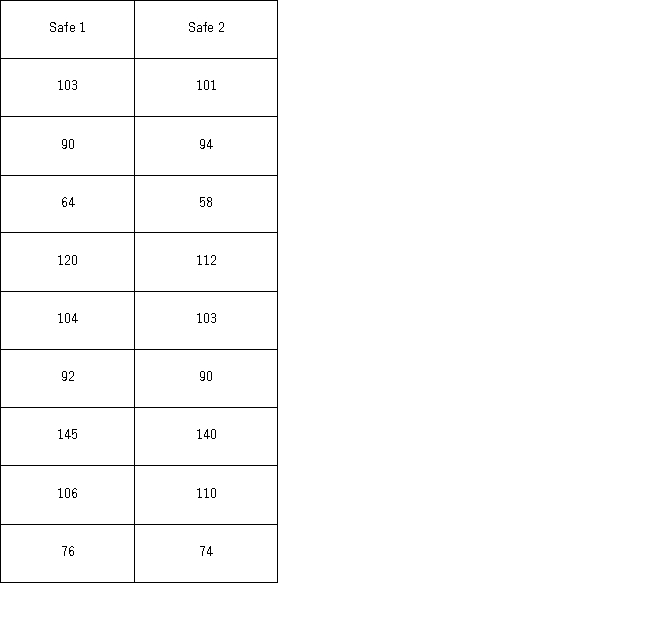 Which of the following hypotheses will determine if the two safes take,on average,the same amount of time to crack?
Which of the following hypotheses will determine if the two safes take,on average,the same amount of time to crack?
A) H0: µD ≤ 0,HA: µD >0
B) H0: µD ≥ 0,HA: µD <0
C) H0: µD ≠ 0,HA: µD =0
D) H0: µD = 0,HA: µD ≠0
 Which of the following hypotheses will determine if the two safes take,on average,the same amount of time to crack?
Which of the following hypotheses will determine if the two safes take,on average,the same amount of time to crack?A) H0: µD ≤ 0,HA: µD >0
B) H0: µD ≥ 0,HA: µD <0
C) H0: µD ≠ 0,HA: µD =0
D) H0: µD = 0,HA: µD ≠0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
64
A tutor promises to improve GMAT scores of students by more than 50 points after three lessons.To see if this is true,the tutor takes a sample of 49 students' test scores after and before they received tutoring.The mean difference was 53 points better after tutoring,with a standard deviation of the difference equal to 12 points.Let µD denote the mean of the difference: score after tutoring minus score before tutoring.Assuming α = 0.05,which of the following is the appropriate critical value?
A) z = 1.677
B) z = 2.011
C) t0.05,48 = 1.677
D) t0.05,48 = 2.011
A) z = 1.677
B) z = 2.011
C) t0.05,48 = 1.677
D) t0.05,48 = 2.011

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
65
A statistics professor at a large university hypothesizes that students who take statistics in the morning typically do better than those who take it in the afternoon.He takes independently random samples,each of size 36,consisting of students who took a morning and an afternoon class,and compares the scores of each group on a common final exam.He finds that the morning group scored an average of 74 with a standard deviation of 8,while the evening group scored an average of 68 with a standard deviation of 10.The population standard deviation of scores is unknown but is assumed to be equal for morning and evening classes.Let µ1 andµ2 represent the population mean final exam scores of statistics' courses offered in the morning and the afternoon,respectively.Compute the appropriate test statistic to analyze the claim at the 1% significance level.
A) t70 = −2.811
B) t70 = 2.811
C) z = −2.811
D) z = 2.811
A) t70 = −2.811
B) t70 = 2.811
C) z = −2.811
D) z = 2.811

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
66
A producer of fine chocolates believes that the sales of two varieties of truffles differ significantly during the holiday season.The first variety is milk chocolate while the second is milk chocolate filled with mint.It is reasonable to assume that truffle sales are normally distributed with unknown but equal population variances.Two independent samples of 18 observations each are collected for the holiday period.A sample mean of 12 million milk chocolate truffles sold with a sample standard deviation of 2.5 million.A sample mean of 13.5 million truffles filled with mint sold with a sample standard deviation of 2.3 million.Use milk chocolate as population 1 and mint chocolate as population 2.Which of the following are the appropriate hypotheses to determine if the average sales of the two varieties of truffles differ significantly during the holiday season?
A) H0: µD ≥ 0,HA: µD <0
B) H0: µD = 0,HA: µD ≠0
C) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
D) H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0
A) H0: µD ≥ 0,HA: µD <0
B) H0: µD = 0,HA: µD ≠0
C) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
D) H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
67
A statistics professor at a large university hypothesizes that students who take statistics in the morning typically do better than those who take it in the afternoon.He takes independently random samples,each of size 36,consisting of students who took a morning and an afternoon class,and compares the scores of each group on a common final exam.He finds that the morning group scored an average of 74 with a standard deviation of 8,while the evening group scored an average of 68 with a standard deviation of 10.The population standard deviation of scores is unknown but is assumed to be equal for morning and evening classes.Let µ1 andµ2 represent the population mean final exam scores of statistics' courses offered in the morning and the afternoon,respectively.At the 1% significance level,does the evidence support the professor's claim?
A) No,because the test statistic is less than the critical value.
B) Yes,because the test statistic is less than the critical value.
C) No,because the test statistic is greater than the critical value.
D) Yes,because the test statistic is greater than the critical value.
A) No,because the test statistic is less than the critical value.
B) Yes,because the test statistic is less than the critical value.
C) No,because the test statistic is greater than the critical value.
D) Yes,because the test statistic is greater than the critical value.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
68
A university wants to compare out-of-state applicants' mean SAT math scores (μ1)to in-state applicants' mean SAT math scores (μ2).The university looks at 35 in-state applicants and 35 out-of-state applicants.The mean SAT math score for in-state applicants was 540,with a standard deviation of 20.The mean SAT math score for out-of-state applicants was 555,with a standard deviation of 25.It is reasonable to assume the corresponding population standard deviations are equal.Calculate a 95% confidence interval for the differenceμ1 - μ2.
A) [-25.6067,-4.3933]
B) [-25.7961,-4.2039]
C) [-25.8124,-4.1876]
D) [-33.6105,3.6105]
A) [-25.6067,-4.3933]
B) [-25.7961,-4.2039]
C) [-25.8124,-4.1876]
D) [-33.6105,3.6105]

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
69
A university wants to compare out-of-state applicants' mean SAT math scores (μ1)to in-state applicants' mean SAT math scores (μ2).The university looks at 35 in-state applicants and 35 out-of-state applicants.The mean SAT math score for in-state applicants was 540,with a standard deviation of 20.The mean SAT math score for out-of-state applicants was 555,with a standard deviation of 25.It is reasonable to assume the corresponding population standard deviations are equal.To calculate the confidence interval for the difference μ1 - μ2,what is the number of degrees of freedom of the appropriate probability distribution?
A) 64
B) 64.87
C) 68
D) 69
A) 64
B) 64.87
C) 68
D) 69

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
70
A new sales training program has been instituted at a rent-to-own company.Prior to the training,10 employees were tested on their knowledge of products offered by the company.Once the training was completed,the employees were tested again in an effort to determine whether the training program was effective.Scores are known to be normally distributed.The sample scores on the tests are listed next.Use pretest score as µ1 for population 1 and posttest score as µ2 for population 2,orµD as the difference calculated as pretest score minus posttest score.Pretest Score 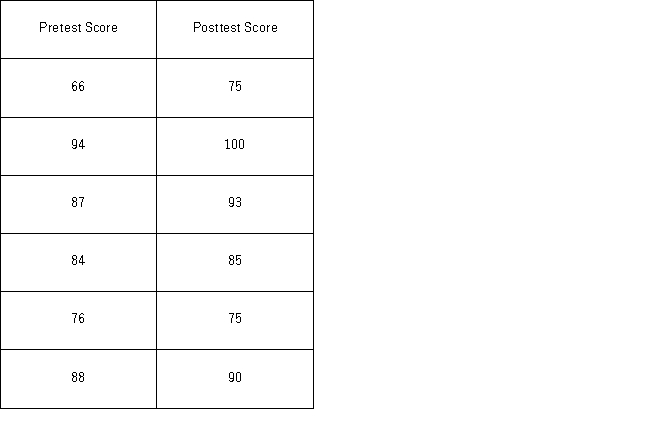 Which of the following is the correct conclusion for the test at α = 0.05?
Which of the following is the correct conclusion for the test at α = 0.05?
A) Given the critical value 1.645,we conclude that training increases scores.
B) Given the critical value 2.015,we conclude that training increases scores.
C) Given the critical value −2.015,we conclude that training increases scores.
D) Given the critical value −1.645,we conclude that training increases scores.
 Which of the following is the correct conclusion for the test at α = 0.05?
Which of the following is the correct conclusion for the test at α = 0.05?A) Given the critical value 1.645,we conclude that training increases scores.
B) Given the critical value 2.015,we conclude that training increases scores.
C) Given the critical value −2.015,we conclude that training increases scores.
D) Given the critical value −1.645,we conclude that training increases scores.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
71
A statistics professor at a large university hypothesizes that students who take statistics in the morning typically do better than those who take it in the afternoon.He takes independently random samples,each of size 36,consisting of students who took a morning and an afternoon class,and compares the scores of each group on a common final exam.He finds that the morning group scored an average of 74 with a standard deviation of 8,while the evening group scored an average of 68 with a standard deviation of 10.The population standard deviation of scores is unknown but is assumed to be equal for morning and evening classes.Let µ1 andµ2 represent the population mean final exam scores of statistics' courses offered in the morning and the afternoon,respectively.Which of the following hypotheses will test the professor's claim?
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: µ1- µ2 > 0,HA: µ1- µ2 ≤ 0
D) H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0
A) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
B) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
C) H0: µ1- µ2 > 0,HA: µ1- µ2 ≤ 0
D) H0: µ1- µ2 = 0,HA: µ1- µ2 ≠ 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
72
A producer of fine chocolates believes that the sales of two varieties of truffles differ significantly during the holiday season.The first variety is milk chocolate while the second is milk chocolate filled with mint.It is reasonable to assume that truffle sales are normally distributed with unknown but equal population variances.Two independent samples of 18 observations each are collected for the holiday period.A sample mean of 12 million milk chocolate truffles sold with a sample standard deviation of 2.5 million.A sample mean of 13.5 million truffles filled with mint sold with a sample standard deviation of 2.3 million.Use milk chocolate as population 1 and mint chocolate as population 2.Which of the following is the appropriate decision given a 5% level of significance?
A) Conclude that the average milk chocolate and mint chocolate sales differ because the p-value is greater than 0.05.
B) Conclude that the average milk chocolate and mint chocolate sales do not differ because the p-value is less than 0.05.
C) Do not conclude that the average milk chocolate and mint chocolate sales differ because the p-value is greater than 0.05.
D) Do not conclude that the average milk chocolate and mint chocolate sales do not differ because the p-value is less than 0.05.
A) Conclude that the average milk chocolate and mint chocolate sales differ because the p-value is greater than 0.05.
B) Conclude that the average milk chocolate and mint chocolate sales do not differ because the p-value is less than 0.05.
C) Do not conclude that the average milk chocolate and mint chocolate sales differ because the p-value is greater than 0.05.
D) Do not conclude that the average milk chocolate and mint chocolate sales do not differ because the p-value is less than 0.05.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
73
A producer of fine chocolates believes that the sales of two varieties of truffles differ significantly during the holiday season.The first variety is milk chocolate while the second is milk chocolate filled with mint.It is reasonable to assume that truffle sales are normally distributed with unknown but equal population variances.Two independent samples of 18 observations each are collected for the holiday period.A sample mean of 12 million milk chocolate truffles sold with a sample standard deviation of 2.5 million.A sample mean of 13.5 million truffles filled with mint sold with a sample standard deviation of 2.3 million.Use milk chocolate as population 1 and mint chocolate as population 2.Assuming the population variances are equal,which of the following is the value of the appropriate test statistic?
A) z = −1.8734
B) z = 1.8734
C) t34 = −1.8734
D) t34 = 1.8734
A) z = −1.8734
B) z = 1.8734
C) t34 = −1.8734
D) t34 = 1.8734

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
74
A statistics professor at a large university hypothesizes that students who take statistics in the morning typically do better than those who take it in the afternoon.He takes independently random samples,each of size 36,consisting of students who took a morning and an afternoon class,and compares the scores of each group on a common final exam.He finds that the morning group scored an average of 74 with a standard deviation of 8,while the evening group scored an average of 68 with a standard deviation of 10.The population standard deviation of scores is unknown but is assumed to be equal for morning and evening classes.Let µ1 andµ2 represent the population mean final exam scores of statistics' courses offered in the morning and the afternoon,respectively.Which of the following is(are)the appropriate critical value(s)to test the professor's claim at the 1% significance level?
A) -2.381 and 2.381
B) -2.326 and 2.326
C) 2.326
D) 2.381
A) -2.381 and 2.381
B) -2.326 and 2.326
C) 2.326
D) 2.381

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
75
A bank is trying to determine which model of safe to install.The bank manager believes that each model is equally resistant to safe crackers but sets up a test to be sure.He hires nine safe experts to break into each of the models,timing each endeavor.The results (in seconds)are given next,paired by expert.Let D be the difference: Time to break Safe 1 minus Time to break Safe 2. ![<strong>A bank is trying to determine which model of safe to install.The bank manager believes that each model is equally resistant to safe crackers but sets up a test to be sure.He hires nine safe experts to break into each of the models,timing each endeavor.The results (in seconds)are given next,paired by expert.Let D be the difference: Time to break Safe 1 minus Time to break Safe 2. Assuming the difference D is normally distributed,which of the following is the 95% confidence interval for μ<sub>D</sub>?</strong> A) [-1.7537,5.7537] B) [-1.1459,5.1459] C) [-0.6739,4.6739] D) [-0.5368,4.5368]](https://storage.examlex.com/TB4266/11eab0ce_310d_0621_a083_7b94e0d78da8_TB4266_00.jpg) Assuming the difference D is normally distributed,which of the following is the 95% confidence interval for μD?
Assuming the difference D is normally distributed,which of the following is the 95% confidence interval for μD?
A) [-1.7537,5.7537]
B) [-1.1459,5.1459]
C) [-0.6739,4.6739]
D) [-0.5368,4.5368]
![<strong>A bank is trying to determine which model of safe to install.The bank manager believes that each model is equally resistant to safe crackers but sets up a test to be sure.He hires nine safe experts to break into each of the models,timing each endeavor.The results (in seconds)are given next,paired by expert.Let D be the difference: Time to break Safe 1 minus Time to break Safe 2. Assuming the difference D is normally distributed,which of the following is the 95% confidence interval for μ<sub>D</sub>?</strong> A) [-1.7537,5.7537] B) [-1.1459,5.1459] C) [-0.6739,4.6739] D) [-0.5368,4.5368]](https://storage.examlex.com/TB4266/11eab0ce_310d_0621_a083_7b94e0d78da8_TB4266_00.jpg) Assuming the difference D is normally distributed,which of the following is the 95% confidence interval for μD?
Assuming the difference D is normally distributed,which of the following is the 95% confidence interval for μD?A) [-1.7537,5.7537]
B) [-1.1459,5.1459]
C) [-0.6739,4.6739]
D) [-0.5368,4.5368]

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
76
A tutor promises to improve GMAT scores of students by more than 50 points after three lessons.To see if this is true,the tutor takes a sample of 49 students' test scores after and before they received tutoring.The mean difference was 53 points better after tutoring,with a standard deviation of the difference equal to 12 points.Let µD denote the mean of the difference: score after tutoring minus score before tutoring.Which of the following is the appropriate conclusion at the 5% significance level?
A) Reject H0;we can conclude that the mean difference in test scores after and before tutoring is greater than 50 points.
B) Reject H0;we cannot conclude that the mean difference in test scores after and before tutoring is greater than 50 points.
C) Fail to reject H0,we can conclude that the mean difference in test scores after and before tutoring is greater than 50 points.
D) Fail to reject H0;we cannot conclude that the mean difference in test scores after and before tutoring is greater than 50 points.
A) Reject H0;we can conclude that the mean difference in test scores after and before tutoring is greater than 50 points.
B) Reject H0;we cannot conclude that the mean difference in test scores after and before tutoring is greater than 50 points.
C) Fail to reject H0,we can conclude that the mean difference in test scores after and before tutoring is greater than 50 points.
D) Fail to reject H0;we cannot conclude that the mean difference in test scores after and before tutoring is greater than 50 points.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
77
A 7,000-seat theater is interested in determining whether there is a difference in attendance between shows on Tuesday evening and those on Wednesday evening.Two independent samples of 25 weeks are collected for Tuesday and Wednesday.The mean attendance on Tuesday evening is calculated as 5,500,while the mean attendance on Wednesday evening is calculated as 5,850.The known population standard deviation for attendance on Tuesday evening is 550 and the known population standard deviation for attendance on Wednesday evening is 445.Which of the following is the appropriate decision given a 5% level of significance?
A) Conclude that the mean attendance differs because the p-value = 0.0067 < 0.05.
B) Conclude that the mean attendance differs because the p-value = 0.0134 < 0.05.
C) Do not conclude that the mean attendance differs because the p-value = 0.0067 < 0.05.
D) Do not conclude that the mean attendance differs because the p-value = 0.0134 < 0.05.
A) Conclude that the mean attendance differs because the p-value = 0.0067 < 0.05.
B) Conclude that the mean attendance differs because the p-value = 0.0134 < 0.05.
C) Do not conclude that the mean attendance differs because the p-value = 0.0067 < 0.05.
D) Do not conclude that the mean attendance differs because the p-value = 0.0134 < 0.05.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
78
A new sales training program has been instituted at a rent-to-own company.Prior to the training,10 employees were tested on their knowledge of products offered by the company.Once the training was completed,the employees were tested again in an effort to determine whether the training program was effective.Scores are known to be normally distributed.The sample scores on the tests are listed next.Use pretest score as µ1 for population 1 and posttest score as µ2 for population 2,orµD as the difference calculated as pretest score minus posttest score. 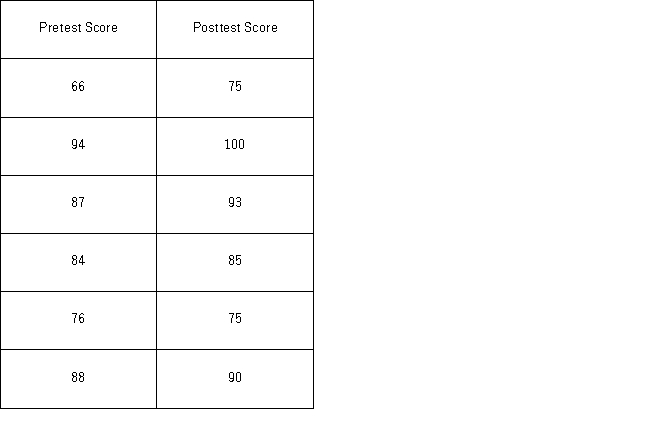 Which of the following is the value of the appropriate test statistic?
Which of the following is the value of the appropriate test statistic?
A) t5 = −2.4947
B) t5 = 2.4947
C) z = −2.4947
D) z = 2.4947
 Which of the following is the value of the appropriate test statistic?
Which of the following is the value of the appropriate test statistic?A) t5 = −2.4947
B) t5 = 2.4947
C) z = −2.4947
D) z = 2.4947

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
79
A tutor promises to improve GMAT scores of students by more than 50 points after three lessons.To see if this is true,the tutor takes a sample of 49 students' test scores after and before they received tutoring.The mean difference was 53 points better after tutoring,with a standard deviation of the difference equal to 12 points.Let µD denote the mean of the difference: score after tutoring minus score before tutoring.Which of the following is the correct value of the test statistic?
A) z = 1.7143
B) z = 1.7500
C) t48 = 1.7143
D) t48 = 1.7500
A) z = 1.7143
B) z = 1.7500
C) t48 = 1.7143
D) t48 = 1.7500

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
80
A new sales training program has been instituted at a rent-to-own company.Prior to the training,10 employees were tested on their knowledge of products offered by the company.Once the training was completed,the employees were tested again in an effort to determine whether the training program was effective.Scores are known to be normally distributed.The sample scores on the tests are listed next.Use pretest score as µ1 for population 1 and posttest score as µ2 for population 2,orµD as the mean of the difference calculated as pretest score minus posttest score. 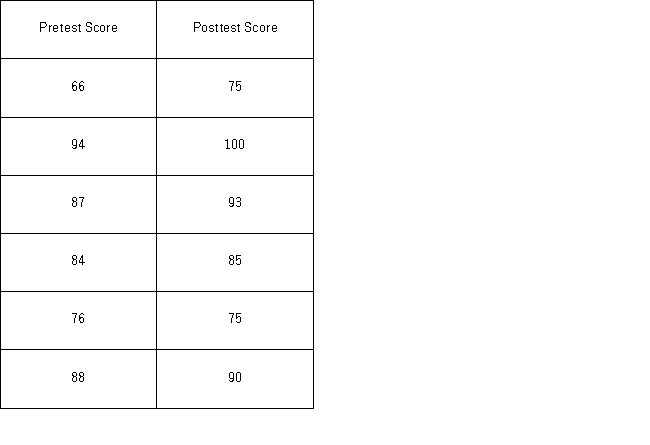 Which of the following are the appropriate hypotheses to determine if the training increases scores?
Which of the following are the appropriate hypotheses to determine if the training increases scores?
A) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
B) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
C) H0: µD ≥ 0,HA: µD <0
D) H0: µD ≤ 0,HA: µD >0
 Which of the following are the appropriate hypotheses to determine if the training increases scores?
Which of the following are the appropriate hypotheses to determine if the training increases scores?A) H0: µ1- µ2 ≥ 0,HA: µ1- µ2 < 0
B) H0: µ1- µ2 ≤ 0,HA: µ1- µ2 > 0
C) H0: µD ≥ 0,HA: µD <0
D) H0: µD ≤ 0,HA: µD >0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck


