Deck 6: Transportation, Transshipment, and Assignment Problems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/98
Play
Full screen (f)
Deck 6: Transportation, Transshipment, and Assignment Problems
1
In a transportation problem, items are allocated from sources to destinations at a minimum cost.
True
2
An assignment problem is a special form of transportation problem.
True
3
For most real-world applications, an unbalanced transportation model is a more likely occurrence than a balanced transportation model.
True
4
In a transportation problem, items are allocated from sources to destinations at a maximum value.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
5
In a transshipment problem, items may be transported directly from sources to destinations.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
6
In an unbalanced transportation problem, if demand exceeds supply, the optimal solution will be infeasible.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
7
In a balanced transportation model where supply equals demand, all constraints are equalities.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
8
In a transshipment problem, items may be transported from one transshipment point to another.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
9
The linear programming model for a transportation problem has constraints for supply at each source and demand at each destination.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
10
A prohibited route in a transportation model should be assigned an arbitrarily high cost coefficient.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
11
A prohibited route in a transportation model should be assigned a value of zero.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
12
In order to model a "prohibited route" in a transportation or transshipment problem, the route should be omitted from the linear program.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
13
In a transshipment problem, items may be transported from one source to another.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
14
An assignment problem is a special form of transportation problem where all supply and demand values equal 1.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
15
In a transshipment problem, items may be transported from destination to destination and from source to source.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
16
In a transshipment problem, items may be transported from sources through transshipment points on to destinations.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
17
The transshipment model includes intermediate points between the sources and destinations.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
18
In an unbalanced transportation model, all constraints are equalities.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
19
In a transshipment problem, items may be transported from one destination to another.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
20
Assignment linear programs always result in integer solutions.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
21
In a ________ problem, items are allocated from sources to destinations at a minimum cost.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
22
The ________ model is an extension of the transportation model in which intermediate points are added between the sources and destinations.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
23
In a ________ transportation model where supply equals demand, all constraints are equalities.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
24
In order to model a "prohibited route" in a transportation or transshipment problem, the cost assigned to the route should be ________.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
25
A form of the transportation problem in which all supply and demand values equal 1 is the ________ problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
26
Assignment problems are always balanced.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
27
An example of a ________ point is a distribution center or warehouse located between plants and stores.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
28
In a linear programming formulation of a transportation model, each of the possible combinations of supply and demand locations is a(n) ________

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
29
In most real-world cases, the supply capacity and demanded amounts result in a(n) ________ transportation model.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
30
In a transshipment model, the supply at each source and demand at each destination are limited to one unit.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
31
In an unbalanced transportation problem, if supply exceeds demand, the shadow price for at least one of the supply constraints will be equal to ________.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
32
For an assignment model, all the supply and demand values are ________.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
33
If the number of sources is greater than the number of destinations, then we have a(n) ________ assignment problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
34
The cost to send a unit of product from supply source A to demand location B would be represented in the ________ of the linear programming statements.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
35
A plant has four jobs to be assigned to four machines, and each machine has different manufacturing times for each product. The production manager wants to determine the optimal assignments of four jobs to four machines to minimize total manufacturing time. This problem can be most efficiently solved using the ________ model.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
36
Networks may be used to represent assignment problems.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
37
In order to prevent the accumulation of inventory at transshipment points, they should be modeled as being ________ nodes.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
38
In an assignment problem, all demand and supply values are equal to ________.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
39
An appropriate choice of a model for analyzing the best shipping routes for a supply chain consisting of a manufacturer, warehouse, and retailer would be the ________ model.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
40
A logistics specialist for Wiethoff Inc. must distribute cases of parts from three factories to three assembly plants. The monthly supplies and demands, along with the per-case transportation costs are:
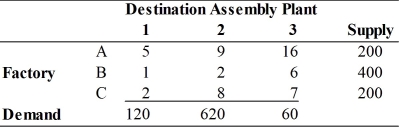
If 120 units are shipped from Factory C to Assembly Plant 1, 60 units from Factory C to Assembly Plant 3, and 400 units from Factory B to Assembly Plant 2, what are the remaining shipments?

If 120 units are shipped from Factory C to Assembly Plant 1, 60 units from Factory C to Assembly Plant 3, and 400 units from Factory B to Assembly Plant 2, what are the remaining shipments?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
41
A logistics specialist for Wiethoff Inc. must distribute cases of parts from three factories to three assembly plants. The monthly supplies and demands, along with the per-case transportation costs are:

What is the objective function for the linear programming formulation of this problem?

What is the objective function for the linear programming formulation of this problem?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
42
Write the assignment problem matrix below as a network flow problem. Assume that the numbers in each cell represent the travel distance required between nodes. The dash indicates that there is not a route between nodes.
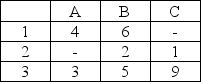


Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
43
A large book publisher has five manuscripts that must be edited as soon as possible. Five editors are available for doing the work, however their working times on the various manuscripts will differ based on their backgrounds and interests. The publisher wants to use an assignment method to determine who does what manuscript. Estimates of editing times (in hours) for each manuscript by each editor is:
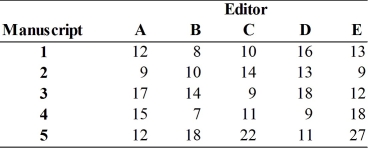
What are the linear programming constraints for manuscript 1 and editor C?

What are the linear programming constraints for manuscript 1 and editor C?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
44
In setting up the an intermediate (transshipment) node constraint, assume that there are three sources, two intermediate nodes, and two destinations, and travel is possible between all sources and the intermediate nodes and between all intermediate nodes and all destinations for a given transshipment problem. In addition, assume that no travel is possible between source nodes, between intermediate nodes, and between destination nodes, and no direct travel from source nodes to destination nodes. Let the source nodes be labeled as 1, 2, 3, the intermediate nodes be labeled as 4 and 5, and the destination nodes be labeled as 6 and 7.
State the constraint for intermediate node 4.
State the constraint for intermediate node 4.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
45
Awards committees need to be formed to review potential award recipients. In the past, three people have been assigned to review each applicant. The only stipulation is that a reviewer cannot be assigned to an applicant if the applicant is a co-worker. The matrix below shows 9 reviewers, 3 candidates, and a matrix. If an entry in the matrix contains an "X", then that specific reviewer is ineligible to review an applicant's material. For example, reviewer 1 cannot review materials submitted by candidate B. It is possible that some reviewers may not receive an assignment.
Applicant
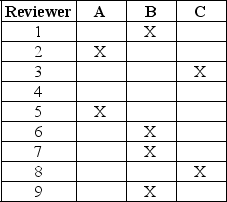
Formulate this as an assignment problem in which two reviewers are assigned to review each applicant's material.
Applicant

Formulate this as an assignment problem in which two reviewers are assigned to review each applicant's material.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
46
If the optimal solution includes x11 = 100 and x22 = 200, determine the remaining shipments that will result in a minimum cost of $1700.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
47
A logistics specialist for Wiethoff Inc. must distribute cases of parts from three factories to three assembly plants. The monthly supplies and demands, along with the per-case transportation costs are:

What are the total monthly transportation costs for the optimal solution?

What are the total monthly transportation costs for the optimal solution?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
48
A large book publisher has five manuscripts that must be edited as soon as possible. Five editors are available for doing the work, however their working times on the various manuscripts will differ based on their backgrounds and interests. The publisher wants to use an assignment method to determine who does what manuscript. Estimates of editing times (in hours) for each manuscript by each editor is:

If the optimal assignments include manuscript 1 to editor B, manuscript 2 to editor E, and manuscript 3 to editor C with a total editing time of 47 minutes, what manuscripts are assigned to editors D and A?

If the optimal assignments include manuscript 1 to editor B, manuscript 2 to editor E, and manuscript 3 to editor C with a total editing time of 47 minutes, what manuscripts are assigned to editors D and A?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
49
A large book publisher has five manuscripts that must be edited as soon as possible. Five editors are available for doing the work, however their working times on the various manuscripts will differ based on their backgrounds and interests. The publisher wants to use an assignment method to determine who does what manuscript. Estimates of editing times (in hours) for each manuscript by each editor is:

a) How many supply-side constraints are needed?
b) How many demand-side constraints are needed?
c) How many variables are involved in this assignment method?

a) How many supply-side constraints are needed?
b) How many demand-side constraints are needed?
c) How many variables are involved in this assignment method?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
50
Consider the following transportation problem:
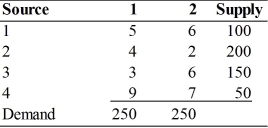
How many supply-side constraints are there? Write the supply-side constraints.

How many supply-side constraints are there? Write the supply-side constraints.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
51
Awards committees need to be formed to review potential award recipients. In the past, three people have been assigned to review each applicant. The only stipulation is that a reviewer cannot be assigned to an applicant if the applicant is a co-worker. The matrix below shows 9 reviewers, 3 candidates, and a matrix. If an entry in the matrix contains an "X", then that specific reviewer is ineligible to review an applicant's material. For example, reviewer 1 cannot review materials submitted by candidate B. It is possible that some reviewers may not receive an assignment.
Applicant

The committee would like to assign three reviewers to each applicant. A partial solution to this problem is shown below, where the number 1 indicates when a reviewer is assigned to an applicant. Assign reviewers to Applicant B and Applicant C.
Applicant
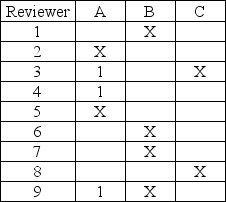
Applicant

The committee would like to assign three reviewers to each applicant. A partial solution to this problem is shown below, where the number 1 indicates when a reviewer is assigned to an applicant. Assign reviewers to Applicant B and Applicant C.
Applicant


Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
52
A logistics specialist for Wiethoff Inc. must distribute cases of parts from three factories to three assembly plants. The monthly supplies and demands, along with the per-case transportation costs are:

What are the supply constraints for the factories?

What are the supply constraints for the factories?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
53
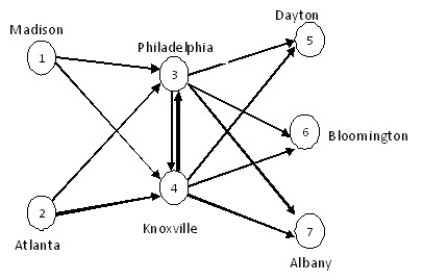
Madlantic Devices designs and manufactures high-end medical devices. The facilities in Madison and Atlanta serve as design and component manufacturing facilities. Components are then shipped to warehouses in Philadelphia or Knoxville, where they are held until final assembly is completed at either Dayton, Bloomington, or Albany.
Manufacturing capacity in Madison and Atlanta is 1000 units. Demand at Dayton, Bloomington, and Albany is 450, 500, and 610, respectively.
The network representing the shipping routs is shown below.
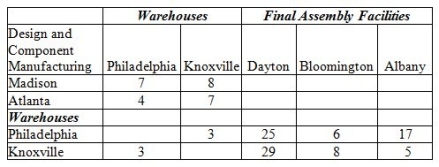
 The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
What is the constraint for Bloomington?
Manufacturing capacity in Madison and Atlanta is 1000 units. Demand at Dayton, Bloomington, and Albany is 450, 500, and 610, respectively.
The network representing the shipping routs is shown below.
 The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
What is the constraint for Bloomington?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
54
In setting up the an intermediate (transshipment) node constraint, assume that there are three sources, two intermediate nodes, and two destinations, and travel is possible between all sources and the intermediate nodes and between all intermediate nodes and all destinations for a given transshipment problem. In addition, assume that no travel is possible between source nodes, between intermediate nodes, and between destination nodes, and no direct travel from source nodes to destination nodes. Let the source nodes be labeled as 1, 2, 3, the intermediate nodes be labeled as 4 and 5, and the destination nodes be labeled as 6 and 7.
If there are 300 units available at source 2, state the constraint for source node 2.
If there are 300 units available at source 2, state the constraint for source node 2.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
55
A logistics specialist for Wiethoff Inc. must distribute cases of parts from three factories to three assembly plants. The monthly supplies and demands, along with the per-case transportation costs are:

What are the demand constraints for the assembly plants?

What are the demand constraints for the assembly plants?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
56
Madlantic Devices designs and manufactures high-end medical devices. The facilities in Madison and Atlanta serve as design and component manufacturing facilities. Components are then shipped to warehouses in Philadelphia or Knoxville, where they are held until final assembly is completed at either Dayton, Bloomington, or Albany.
Manufacturing capacity in Madison and Atlanta is 1000 units. Demand at Dayton, Bloomington, and Albany is 450, 500, and 610, respectively.
The network representing the shipping routs is shown below.
 The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.

What is the constraint for the transshipment node in Knoxville?
Manufacturing capacity in Madison and Atlanta is 1000 units. Demand at Dayton, Bloomington, and Albany is 450, 500, and 610, respectively.
The network representing the shipping routs is shown below.
 The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
What is the constraint for the transshipment node in Knoxville?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
57
Madlantic Devices designs and manufactures high-end medical devices. The facilities in Madison and Atlanta serve as design and component manufacturing facilities. Components are then shipped to warehouses in Philadelphia or Knoxville, where they are held until final assembly is completed at either Dayton, Bloomington, or Albany.
Manufacturing capacity in Madison and Atlanta is 1000 units. Demand at Dayton, Bloomington, and Albany is 450, 500, and 610, respectively.
The network representing the shipping routs is shown below.
 The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.

What is the objective function for this problem? Use the notation Xij, where i and j correspond to the node numbers indicated in the diagram.
Manufacturing capacity in Madison and Atlanta is 1000 units. Demand at Dayton, Bloomington, and Albany is 450, 500, and 610, respectively.
The network representing the shipping routs is shown below.
 The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
The costs for shipping between each facility is shown below. A blank cell indicates that shipping between two facilities is not permitted.
What is the objective function for this problem? Use the notation Xij, where i and j correspond to the node numbers indicated in the diagram.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the following transportation problem:

How many demand-side constraints are there? Write the demand-side constraints.

How many demand-side constraints are there? Write the demand-side constraints.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
59
In setting up the an intermediate (transshipment) node constraint, assume that there are three sources, two intermediate nodes, and two destinations, and travel is possible between all sources and the intermediate nodes and between all intermediate nodes and all destinations for a given transshipment problem. In addition, assume that no travel is possible between source nodes, between intermediate nodes, and between destination nodes, and no direct travel from source nodes to destination nodes. Let the source nodes be labeled as 1, 2, 3, the intermediate nodes be labeled as 4 and 5, and the destination nodes be labeled as 6 and 7.
If there are 175 units demanded at destination 6, state the constraint for destination 6.
If there are 175 units demanded at destination 6, state the constraint for destination 6.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
60
Awards committees need to be formed to review potential award recipients. In the past, three people have been assigned to review each applicant. The only stipulation is that a reviewer cannot be assigned to an applicant if the applicant is a co-worker. The matrix below shows 9 reviewers, 3 candidates, and a matrix. If an entry in the matrix contains an "X", then that specific reviewer is ineligible to review an applicant's material. For example, reviewer 1 cannot review materials submitted by candidate B. It is possible that some reviewers may not receive an assignment.
Applicant

A partial solution to this problem is shown below, where the number 1 indicates when a reviewer is assigned to an applicant. Assign two reviewers to Applicant B and 1 additional reviewer to Applicant C.
Applicant
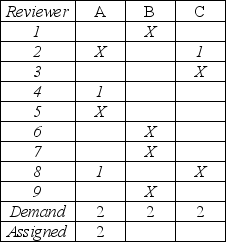
Applicant

A partial solution to this problem is shown below, where the number 1 indicates when a reviewer is assigned to an applicant. Assign two reviewers to Applicant B and 1 additional reviewer to Applicant C.
Applicant


Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
61
In a balanced transportation model where supply equals demand,
A) all constraints are equalities.
B) none of the constraints are equalities.
C) all constraints are inequalities.
D) none of the constraints are inequalities.
A) all constraints are equalities.
B) none of the constraints are equalities.
C) all constraints are inequalities.
D) none of the constraints are inequalities.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
62
The following table represents the cost to ship from Distribution Center 1, 2, or 3 to
Customer A, B, or C.
-The constraint that represents the quantity demanded by Customer B is:
A) 6X1B + 2X2B + 8X3B ? 350
B) 6X1B + 2X2B + 8X3B = 350
C) X1B + X2B + X3B ? 350
D) X1B + X2B + X3B = 350
Customer A, B, or C.
-The constraint that represents the quantity demanded by Customer B is:
A) 6X1B + 2X2B + 8X3B ? 350
B) 6X1B + 2X2B + 8X3B = 350
C) X1B + X2B + X3B ? 350
D) X1B + X2B + X3B = 350

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
63
Due to increased sales, a company is considering building three new distribution centers (DCs) to serve four regional sales areas. The annual cost to operate DC 1 is $500 (in thousands of dollars). The cost to operate DC 2 is $600 (in thousands of dollars.). The cost to operate DC 3 is $525 (in thousands of dollars). Assume that the variable cost of operating at each location is the same, and therefore not a consideration in making the location decision.
The table below shows the cost ($ per item) for shipping from each DC to each region.
Region
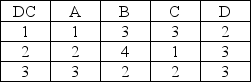
The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units.
Write the constraints for the 3 distribution centers.
The table below shows the cost ($ per item) for shipping from each DC to each region.
Region

The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units.
Write the constraints for the 3 distribution centers.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
64
The following table represents the cost to ship from Distribution Center 1, 2, or 3 to
Customer A, B, or C.
-The constraint that represents the quantity supplied by DC 1 is:
A) 4X1A + 6X1B + 8X1C ? 500
B) 4X1A + 6X1B + 8X1C = 500
C) X1A + X1B + X1C ? 500
D) X1A + X1B + X1C =500
Customer A, B, or C.
-The constraint that represents the quantity supplied by DC 1 is:
A) 4X1A + 6X1B + 8X1C ? 500
B) 4X1A + 6X1B + 8X1C = 500
C) X1A + X1B + X1C ? 500
D) X1A + X1B + X1C =500

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
65
Consider the following network representation of shipment routes between plants, a distribution center, and retail outlets. The numbers next to the arcs represent shipping costs. For example, the cost of shipping from plant 1 to distribution center 3 is equal to $2.
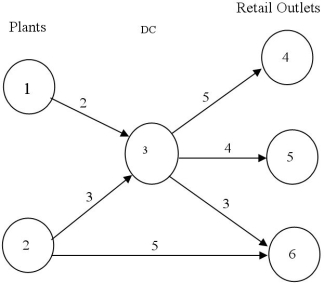 Assume that Plant 1 can supply 400 units and Plant 2, 500 units. Demand at the retail outlets are: Outlet 4, 300 units; Outlet 5, 250 units; Outlet 6, 450 units.
Assume that Plant 1 can supply 400 units and Plant 2, 500 units. Demand at the retail outlets are: Outlet 4, 300 units; Outlet 5, 250 units; Outlet 6, 450 units.
Which constraint represents transshipment through the distribution center?
A) 2X13 + 3X23 = 900
B) 2X13 + 3X23 + 5X34 + 4X35 + 3X36 = 0
C) X13 + X23 - X34 - X35 - X36 = 0
D) X13 + X23 - X34 - X35 - X36 ≥ 0
 Assume that Plant 1 can supply 400 units and Plant 2, 500 units. Demand at the retail outlets are: Outlet 4, 300 units; Outlet 5, 250 units; Outlet 6, 450 units.
Assume that Plant 1 can supply 400 units and Plant 2, 500 units. Demand at the retail outlets are: Outlet 4, 300 units; Outlet 5, 250 units; Outlet 6, 450 units.Which constraint represents transshipment through the distribution center?
A) 2X13 + 3X23 = 900
B) 2X13 + 3X23 + 5X34 + 4X35 + 3X36 = 0
C) X13 + X23 - X34 - X35 - X36 = 0
D) X13 + X23 - X34 - X35 - X36 ≥ 0

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
66
The linear programming model for a transportation problem has constraints for supply at each ________ and ________ at each destination.
A) destination, source
B) source, destination
C) demand, source
D) source, demand
A) destination, source
B) source, destination
C) demand, source
D) source, demand

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
67
Which of the following assumptions is not an assumption of the transportation model?
A) Shipping costs per unit are constant.
B) There is one transportation route between each source and destination.
C) There is one transportation mode between each source and destination.
D) Actual total supply and actual total demand must be equal.
A) Shipping costs per unit are constant.
B) There is one transportation route between each source and destination.
C) There is one transportation mode between each source and destination.
D) Actual total supply and actual total demand must be equal.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
68
Sketch the network for this problem and label all nodes and arrows with the appropriate information.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
69
Due to increased sales, a company is considering building three new distribution centers (DCs) to serve four regional sales areas. The annual cost to operate DC 1 is $500 (in thousands of dollars). The cost to operate DC 2 is $600 (in thousands of dollars.). The cost to operate DC 3 is $525 (in thousands of dollars). Assume that the variable cost of operating at each location is the same, and therefore not a consideration in making the location decision.
The table below shows the cost ($ per item) for shipping from each DC to each region.
Region
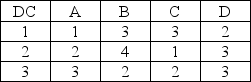
The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units.
Write the objective function for this problem.
The table below shows the cost ($ per item) for shipping from each DC to each region.
Region

The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units.
Write the objective function for this problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
70
Companies A, B, and C supply components to three plants (F, G, and H) via two crossdocking facilities (D and E). It costs $4 to ship from D regardless of final destination and $3 to ship to E regardless of supplier. Shipping to D from A, B, and C costs $3, $4, and $5, respectively, and shipping from E to F, G, and H costs $10, $9, and $8, respectively. Suppliers A, B, and C can provide 200, 300 and 500 units respectively and plants F, G, and H need 350, 450, and 200 units respectively. Crossdock facilities D and E can handle 600 and 700 units, respectively. Logistics Manager, Aretha Franklin, had previously used "Chain of Fools" as her supply chain consulting company, but now turns to you for some solid advice.
What is the complete linear model for this scenario?
What is the complete linear model for this scenario?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
71
In a transshipment problem, items may be transported
A) from destination to destination.
B) from one transshipment point to another.
C) directly from sources to destinations.
D) all of the above
A) from destination to destination.
B) from one transshipment point to another.
C) directly from sources to destinations.
D) all of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
72
The assignment problem constraint x41 + x42 + x43 + x44 ≤ 3 means
A) agent 3 can be assigned to 4 tasks.
B) agent 4 can be assigned to 3 tasks.
C) a mixture of agents 1, 2, 3 and 4 will be assigned to tasks 1, 2 or 3.
D) There is no feasible solution.
A) agent 3 can be assigned to 4 tasks.
B) agent 4 can be assigned to 3 tasks.
C) a mixture of agents 1, 2, 3 and 4 will be assigned to tasks 1, 2 or 3.
D) There is no feasible solution.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
73
Due to increased sales, a company is considering building three new distribution centers (DCs) to serve four regional sales areas. The annual cost to operate DC 1 is $500 (in thousands of dollars). The cost to operate DC 2 is $600 (in thousands of dollars.). The cost to operate DC 3 is $525 (in thousands of dollars). Assume that the variable cost of operating at each location is the same, and therefore not a consideration in making the location decision.
The table below shows the cost ($ per item) for shipping from each DC to each region.
Region
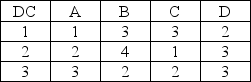
The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units.
Define the decision variables for this situation.
The table below shows the cost ($ per item) for shipping from each DC to each region.
Region

The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units.
Define the decision variables for this situation.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
74
The problem that deals with the distribution of goods from several sources to several destinations is the
A) network problem.
B) assignment problem.
C) transportation problem .
D) transshipment problem.
A) network problem.
B) assignment problem.
C) transportation problem .
D) transshipment problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
75
In the linear programming formulation of a transportation network,
A) there is one variable for each arc.
B) there is one constraint for each node.
C) the sum of variables corresponding to arcs out of an source node is constrained by the supply at that node.
D) all of the above
A) there is one variable for each arc.
B) there is one constraint for each node.
C) the sum of variables corresponding to arcs out of an source node is constrained by the supply at that node.
D) all of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
76
Which of the following are assumptions or requirements of the transportation problem?
A) There must be multiple sources.
B) Goods are the same, regardless of source
C) There must be multiple destinations.
D) There must be multiple routes between each source and each destination.
A) There must be multiple sources.
B) Goods are the same, regardless of source
C) There must be multiple destinations.
D) There must be multiple routes between each source and each destination.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
77
In a transportation problem, items are allocated from sources to destinations
A) at a maximum cost.
B) at a minimum cost.
C) at a minimum profit.
D) at a minimum revenue.
A) at a maximum cost.
B) at a minimum cost.
C) at a minimum profit.
D) at a minimum revenue.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
78
Companies A, B, and C supply components to three plants (F, G, and H) via two crossdocking facilities (D and E). It costs $4 to ship from D regardless of final destination and $3 to ship to E regardless of supplier. Shipping to D from A, B, and C costs $3, $4, and $5, respectively, and shipping from E to F, G, and H costs $10, $9, and $8, respectively. Suppliers A, B, and C can provide 200, 300 and 500 units respectively and plants F, G, and H need 350, 450, and 200 units respectively. Crossdock facilities D and E can handle 600 and 700 units, respectively. Logistics Manager, Aretha Franklin, had previously used "Chain of Fools" as her supply chain consulting company, but now turns to you for some solid advice.
What are the objective function terms that involve the demand locations?
What are the objective function terms that involve the demand locations?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
79
Companies A, B, and C supply components to three plants (F, G, and H) via two crossdocking facilities (D and E). It costs $4 to ship from D regardless of final destination and $3 to ship to E regardless of supplier. Shipping to D from A, B, and C costs $3, $4, and $5, respectively, and shipping from E to F, G, and H costs $10, $9, and $8, respectively. Suppliers A, B, and C can provide 200, 300 and 500 units respectively and plants F, G, and H need 350, 450, and 200 units respectively. Crossdock facilities D and E can handle 600 and 700 units, respectively. Logistics Manager, Aretha Franklin, had previously used "Chain of Fools" as her supply chain consulting company, but now turns to you for some solid advice.
How would the transshipment location constraints read if it was OK to store product there on a temporary basis?
How would the transshipment location constraints read if it was OK to store product there on a temporary basis?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
80
Companies A, B, and C supply components to three plants (F, G, and H) via two crossdocking facilities (D and E). It costs $4 to ship from D regardless of final destination and $3 to ship to E regardless of supplier. Shipping to D from A, B, and C costs $3, $4, and $5, respectively, and shipping from E to F, G, and H costs $10, $9, and $8, respectively. Suppliers A, B, and C can provide 200, 300 and 500 units respectively and plants F, G, and H need 350, 450, and 200 units respectively. Crossdock facilities D and E can handle 600 and 700 units, respectively. Logistics Manager, Aretha Franklin, had previously used "Chain of Fools" as her supply chain consulting company, but now turns to you for some solid advice.
Write every constraint that involves Company A.
Write every constraint that involves Company A.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck


