Deck 3: Linear Programming: Formulation and Applications
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/76
Play
Full screen (f)
Deck 3: Linear Programming: Formulation and Applications
1
Financial planning is one of the most important areas of application for cost-benefit-tradeoff problems.
False
2
In the algebraic form of a resource constraint, the coefficient of each decision variable is the resource usage per unit of the corresponding activity.
True
3
When formulating a linear programming model on a spreadsheet, the decisions to be made are located in the data cells.
False
4
Strict inequalities (i.e., < or >) are not permitted in linear programming formulations.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
5
It is usually quite simple to obtain estimates of parameters in a linear programming problem.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
6
Approximations and simplifying assumptions generally are required to have a workable model.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
7
When formulating a linear programming model on a spreadsheet, the constraints are located (in part) in the output cells.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
8
Linear programming does not permit fractional solutions.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
9
The objective cell is a special kind of output cell.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
10
Resource-allocation problems are linear programming problems involving the allocation of limited resources to activities.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
11
A resource constraint refers to any functional constraint with a ≥ sign in a linear programming model.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
12
A mathematical model will be an exact representation of the real problem.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
13
A key assumption of linear programming is that the equation for each of the output cells, including the objective cell, can be expressed as a SUMPRODUCT (or SUM) function.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
14
For cost-benefit-tradeoff problems, minimum acceptable levels for each kind of benefit are prescribed and the objective is to achieve all these benefits with minimum cost.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
15
In most cases, the minimum acceptable level for a cost-benefit-tradeoff problem is set by how much money is available.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
16
A benefit constraint refers to a functional constraint with a ≥ sign in a linear programming model.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
17
When formulating a linear programming problem on a spreadsheet, data cells will show the levels of activities for the decisions being made.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
18
Cost-benefit-tradeoff problems are linear programming problems involving the allocation of limited resources to activities.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
19
When formulating a linear programming model on a spreadsheet, the measure of performance is located in the objective cell.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
20
When studying a resource-allocation problem, it is necessary to determine the contribution per unit of each activity to the overall measure of performance.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
21
It is the nature of the application that determines the classification of the resulting linear programming formulation.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
22
Once a linear programming problem has been formulated, it is rare to make major adjustments to it.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
23
When dealing with huge real problems, there is no such thing as the perfectly correct linear programming model for the problem.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
24
In an assignment problem, it is necessary to add an integer constraint to the decision variables to ensure that they will take on a value of either 0 or 1.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
25
Generally, assignment problems match people to an equal number of tasks at a minimum cost.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
26
Blending problems are a special type of mixed linear programming problems.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
27
A transportation problem will always return integer values for all decision variables.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
28
The requirements assumption states that each source has a fixed supply of units, where the entire supply must be distributed to the destinations and that each destination has a fixed demand for units, where the entire demand must be received from the sources.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
29
A transportation problem requires a unit cost for every source-destination combination.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
30
It is fairly common to have both resource constraints and benefit constraints in the same formulation.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
31
The capacity row in a distribution-network formulation shows the maximum number of units than can be shipped through the network.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
32
Transportation problems are concerned with distributing commodities from sources to destinations in such a way as to minimize the total distribution cost.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
33
Having one requirement for each location is a characteristic common to all transportation problems.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
34
It is the nature of the restrictions imposed on the decisions regarding the mix of activity levels that determines the classification of the resulting linear programming formulation.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
35
A mixed linear programming problem will always contain some of each of the three types of constraints in it.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
36
Model formulation should precede problem formulation.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
37
Fixed-requirement constraints in a linear programming model are functional constraints that use an equal sign.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
38
Choosing the best tradeoff between cost and benefits is a managerial judgment decision.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
39
An assignment problem is a special type of transportation problem.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
40
Transportation problems always involve shipping goods from one location to another.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
41
Transportation and assignment problems are examples of fixed-requirement problems.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
42
When formulating a linear programming problem on a spreadsheet, which of the following is true?
A) Parameters are called data cells.
B) Decision variables are called changing cells.
C) Right hand sides are part of the constraints.
D) The objective function is called the objective cell.
E) All of the answer choices are correct.
A) Parameters are called data cells.
B) Decision variables are called changing cells.
C) Right hand sides are part of the constraints.
D) The objective function is called the objective cell.
E) All of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
43
In linear programming formulations, it is possible to have the following types of constraints:
A) ≤.
B) >.
C) =.
D) ≤ and > only.
E) All of the answer choices are correct.
A) ≤.
B) >.
C) =.
D) ≤ and > only.
E) All of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
44
A linear programming problem where the objective is to find the best mix of ingredients for a product to meet certain specifications is called:
A) a resource-allocation problem.
B) a blending problem.
C) a cost-benefit tradeoff problem.
D) a mixture problem.
E) None of the answer choices are correct.
A) a resource-allocation problem.
B) a blending problem.
C) a cost-benefit tradeoff problem.
D) a mixture problem.
E) None of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
45
Mixed problems may have the following type of constraints:
A) ≥.
B) ≤.
C) =.
D) All of the answer choices are correct.
E) None of the answer choices are correct.
A) ≥.
B) ≤.
C) =.
D) All of the answer choices are correct.
E) None of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
46
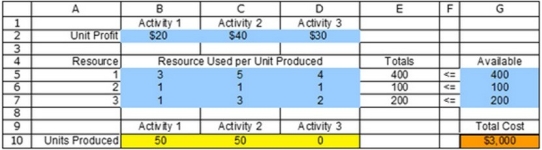 Where is the objective cell located?
Where is the objective cell located?A) B2:D2
B) B2:D2, B4:D7, and G5:G7
C) B10:D10
D) E5:E7
E) G10

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
47
Cost-benefit tradeoff problems have the following type of constraints:
A) ≥
B) ≤
C) =
D) <
E) None of the answer choices are correct.
A) ≥
B) ≤
C) =
D) <
E) None of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
48
The transportation model method for evaluating location alternatives minimizes:
A) the number of sources.
B) the number of destinations.
C) total supply.
D) total demand.
E) total shipping cost.
A) the number of sources.
B) the number of destinations.
C) total supply.
D) total demand.
E) total shipping cost.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
49
Resource-allocation problems have the following type of constraints:
A) ≥.
B) ≤.
C) =.
D) <.
E) None of the answer choices are correct.
A) ≥.
B) ≤.
C) =.
D) <.
E) None of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
50
A linear programming model contains which of the following components?
A) Data.
B) Decisions.
C) Constraints.
D) Measure of performance.
E) All of the answer choices are correct.
A) Data.
B) Decisions.
C) Constraints.
D) Measure of performance.
E) All of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
51
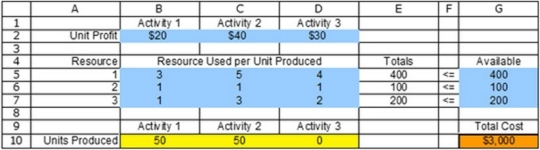 Where are the output cells located?
Where are the output cells located?A) B2:D2
B) B2:D2, B4:D7, and G5:G7
C) B10:D10
D) E5:E7
E) G10

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
52
A transportation problem with 3 factories and 4 customers will have 12 fixed-requirement constraints.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
53
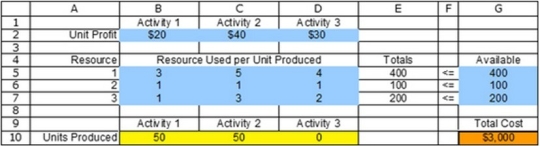 Where are data cells located?
Where are data cells located?A) B2:D2
B) B2:D2, B4:D7, and G5:G7
C) B10:D10
D) E5:E7
E) G10

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
54
Starting with a simple version of a model and adding to it until it reflects the real problem is called:
A) model validation.
B) model enrichment.
C) model enhancement.
D) model elaboration.
E) None of the answer choices are correct.
A) model validation.
B) model enrichment.
C) model enhancement.
D) model elaboration.
E) None of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
55
A transportation problem with 3 factories and 4 customers will have 12 shipping lanes.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
56
In a cost-benefit-trade-off problem, management defines the maximum amount that can be spent and the objective is to maximize benefits within this cost target.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
57
Which of the following are categories of linear programming problems?
A) Resource-allocation problems.
B) Cost-benefit-tradeoff problems.
C) Distribution-network problems.
D) All of the above.
E) None of the above.
A) Resource-allocation problems.
B) Cost-benefit-tradeoff problems.
C) Distribution-network problems.
D) All of the above.
E) None of the above.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
58
A linear programming problem may return fractional solutions for a resource allocation problem.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
59
Using techniques to test the initial versions of a model to identify errors and omissions is called:
A) model validation.
B) model enrichment.
C) model enhancement.
D) model debugging.
E) None of the answer choices are correct.
A) model validation.
B) model enrichment.
C) model enhancement.
D) model debugging.
E) None of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
60
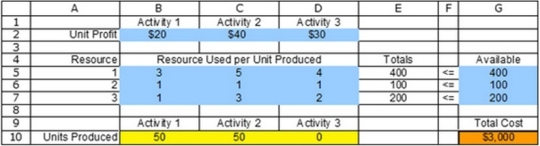 Where are the changing cells located?
Where are the changing cells located?A) B2:D2
B) B2:D2, B4:D7, and G5:G7
C) B10:D10
D) E5:E7
E) G10

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
61
Which of the following is not information needed to use the transportation model?
A) Capacity of the sources.
B) Demand of the destinations.
C) Unit shipping costs.
D) Unit shipping distances.
E) All of the answer choices are correct.
A) Capacity of the sources.
B) Demand of the destinations.
C) Unit shipping costs.
D) Unit shipping distances.
E) All of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
62
When formulating a transportation problem on a spreadsheet, which of the following are necessary?
A) A table of data.
B) A network representation.
C) A table for the solution.
D) A table of data and a table for the solution only.
E) All of the answer choices are correct.
A) A table of data.
B) A network representation.
C) A table for the solution.
D) A table of data and a table for the solution only.
E) All of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
63
A grocery store manager must decide how to best present a limited supply of milk and cookies to its customers. Milk can be sold by itself for a profit of $1.50 per gallon. Cookies can likewise be sold at a profit of $2.50 per dozen. To increase appeal to customers, one gallon of milk and a dozen cookies can be packaged together and are then sold for a profit of $3.00 per bundle. The manager has 100 gallons of milk and 150 dozen cookies available each day. The manager has decided to stock at least 75 gallons of milk per day and demand for cookies is always 140 dozen per day. To maximize profits, how much of each product should the manager stock.
Which of the following is the objective function for the grocer's problem?
A) Max P = 1.5M + 2.5C + 3B
B) Min P = 1.5M + 2.5C + 3B
C) Max P = 2.5M + 1.5C + 3B
D) Max P = 2.5M + 3C + 1.5B
E) Min P = 1.5M + 1.5C + 3B
Which of the following is the objective function for the grocer's problem?
A) Max P = 1.5M + 2.5C + 3B
B) Min P = 1.5M + 2.5C + 3B
C) Max P = 2.5M + 1.5C + 3B
D) Max P = 2.5M + 3C + 1.5B
E) Min P = 1.5M + 1.5C + 3B

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
64
An assignment problem:
A) is a special transportation problem.
B) will always have an integer solution.
C) has all supplies and demands equal to 1.
D) None of the answer choices are correct.
E) All of the answer choices are correct.
A) is a special transportation problem.
B) will always have an integer solution.
C) has all supplies and demands equal to 1.
D) None of the answer choices are correct.
E) All of the answer choices are correct.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
65
A freelance writer must choose how to spend her time working on several different types of projects.
Newspaper stories take 3 hours to write and pay a flat rate of $45 per story. Magazine articles take much longer to write (25 hours) but pay significantly better ($400 per article). Proofreading is often tedious, but the writer can always find proofreading jobs that pay $20 per hour. The writer wants to maximize her income, but doesn't want to work more than 45 hours per week. Additionally, she dislikes proofreading so she would like to spend no more than 7 hours per week on that task. Both newspaper stories and magazine articles must be completed in the week they are started (HINT: use an integer constraint to be sure that all newspaper and magazine jobs are finished within a week).
Which of the following is the constraint that limits the amount of time the writer will work each week?
A) 3N + 25M + P ≥ 45
B) 3N + 25M + P ≤ 45
C) 3N + 25M + P ≤ 7
D) 45N + 400M + 20P ≤ 45
E) 45N + 400M + 20P ≥ 45
Newspaper stories take 3 hours to write and pay a flat rate of $45 per story. Magazine articles take much longer to write (25 hours) but pay significantly better ($400 per article). Proofreading is often tedious, but the writer can always find proofreading jobs that pay $20 per hour. The writer wants to maximize her income, but doesn't want to work more than 45 hours per week. Additionally, she dislikes proofreading so she would like to spend no more than 7 hours per week on that task. Both newspaper stories and magazine articles must be completed in the week they are started (HINT: use an integer constraint to be sure that all newspaper and magazine jobs are finished within a week).
Which of the following is the constraint that limits the amount of time the writer will work each week?
A) 3N + 25M + P ≥ 45
B) 3N + 25M + P ≤ 45
C) 3N + 25M + P ≤ 7
D) 45N + 400M + 20P ≤ 45
E) 45N + 400M + 20P ≥ 45

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
66
Applications of assignment problems may include:
A) matching personnel to jobs.
B) assigning machines to tasks.
C) designing bussing routes.
D) matching personnel to jobs and assigning machines to tasks only.
E) matching personnel to jobs, assigning machines to tasks, and designing bussing routes.
A) matching personnel to jobs.
B) assigning machines to tasks.
C) designing bussing routes.
D) matching personnel to jobs and assigning machines to tasks only.
E) matching personnel to jobs, assigning machines to tasks, and designing bussing routes.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
67
A grocery store manager must decide how to best present a limited supply of milk and cookies to its customers. Milk can be sold by itself for a profit of $1.50 per gallon. Cookies can likewise be sold at a profit of $2.50 per dozen. To increase appeal to customers, one gallon of milk and a dozen cookies can be packaged together and are then sold for a profit of $3.00 per bundle. The manager has 100 gallons of milk and 150 dozen cookies available each day. The manager has decided to stock at least 75 gallons of milk per day and demand for cookies is always 140 dozen per day. To maximize profits, how much of each product should the manager stock.
The manager's problem falls within which classification?
A) Resource-allocation
B) Cost-benefit-trade-off
C) Mixed problems
D) Transportation problems
E) Assignment problems
The manager's problem falls within which classification?
A) Resource-allocation
B) Cost-benefit-trade-off
C) Mixed problems
D) Transportation problems
E) Assignment problems

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
68
A grocery store manager must decide how to best present a limited supply of milk and cookies to its customers. Milk can be sold by itself for a profit of $1.50 per gallon. Cookies can likewise be sold at a profit of $2.50 per dozen. To increase appeal to customers, one gallon of milk and a dozen cookies can be packaged together and are then sold for a profit of $3.00 per bundle. The manager has 100 gallons of milk and 150 dozen cookies available each day. The manager has decided to stock at least 75 gallons of milk per day and demand for cookies is always 140 dozen per day. To maximize profits, how much of each product should the manager stock.
Which of the following is the constraint that limits the amount of milk the store will use (both in bundles and sold separately) each day?
A) M + B ≥ 100
B) M + B ≤ 100
C) M + B ≥ 75
D) M + B ≤ 75
E) M ≤ 100
Which of the following is the constraint that limits the amount of milk the store will use (both in bundles and sold separately) each day?
A) M + B ≥ 100
B) M + B ≤ 100
C) M + B ≥ 75
D) M + B ≤ 75
E) M ≤ 100

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
69
A firm has 4 plants that produce widgets. Plants A, B, and C can each produce 100 widgets per day. Plant D can produce 50 widgets per day. Each day, the widgets produced in the plants must be shipped to satisfy the demand of 3 customers. Customer 1 requires 75 units per day, customer 2 requires 100 units per day, and customer 3 requires 175 units per day. The shipping costs for each possible route are shown in the table below:
The firm needs to satisfy all demand each day, but would like to minimize the total costs.
The objective function for the firm's problem will have how many terms?
A) 5
B) 7
C) 10
D) 12
E) 14
The firm needs to satisfy all demand each day, but would like to minimize the total costs.
The objective function for the firm's problem will have how many terms?
A) 5
B) 7
C) 10
D) 12
E) 14

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
70
A grocery store manager must decide how to best present a limited supply of milk and cookies to its customers. Milk can be sold by itself for a profit of $1.50 per gallon. Cookies can likewise be sold at a profit of $2.50 per dozen. To increase appeal to customers, one gallon of milk and a dozen cookies can be packaged together and are then sold for a profit of $3.00 per bundle. The manager has 100 gallons of milk and 150 dozen cookies available each day. The manager has decided to stock at least 75 gallons of milk per day and demand for cookies is always 140 dozen per day. To maximize profits, how much of each product should the manager stock.
What is the maximum daily profit that the grocery store can achieve?
A) $515
B) $485
C) $455
D) $425
E) $395
What is the maximum daily profit that the grocery store can achieve?
A) $515
B) $485
C) $455
D) $425
E) $395

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
71
A firm has 4 plants that produce widgets. Plants A, B, and C can each produce 100 widgets per day. Plant D can produce 50 widgets per day. Each day, the widgets produced in the plants must be shipped to satisfy the demand of 3 customers. Customer 1 requires 75 units per day, customer 2 requires 100 units per day, and customer 3 requires 175 units per day. The shipping costs for each possible route are shown in the table below:
The firm needs to satisfy all demand each day, but would like to minimize the total costs.
Which of the following constraints is unnecessary for this problem (xi,j is the number of widgets shipped from factory i to customer j)?
A) xA,1 + xA,2 + xA,3 ? 100
B) xB,1 + xB,2 + xB,3 ? 100
C) xC,1 + xxC,2 + xxC,3 ? 100
D) xA,1 + xB,1 + xxC,1 ? 75
E) xA,1, xA,2, xA,3, xB,1, xB,2, xB,3, xC,1, xC,2, xC,3 integer
The firm needs to satisfy all demand each day, but would like to minimize the total costs.
Which of the following constraints is unnecessary for this problem (xi,j is the number of widgets shipped from factory i to customer j)?
A) xA,1 + xA,2 + xA,3 ? 100
B) xB,1 + xB,2 + xB,3 ? 100
C) xC,1 + xxC,2 + xxC,3 ? 100
D) xA,1 + xB,1 + xxC,1 ? 75
E) xA,1, xA,2, xA,3, xB,1, xB,2, xB,3, xC,1, xC,2, xC,3 integer

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
72
A freelance writer must choose how to spend her time working on several different types of projects.
Newspaper stories take 3 hours to write and pay a flat rate of $45 per story. Magazine articles take much longer to write (25 hours) but pay significantly better ($400 per article). Proofreading is often tedious, but the writer can always find proofreading jobs that pay $20 per hour. The writer wants to maximize her income, but doesn't want to work more than 45 hours per week. Additionally, she dislikes proofreading so she would like to spend no more than 7 hours per week on that task. Both newspaper stories and magazine articles must be completed in the week they are started (HINT: use an integer constraint to be sure that all newspaper and magazine jobs are finished within a week).
The writer's problem falls within which classification?
A) Resource-allocation.
B) Cost-benefit-trade-off.
C) Mixed problems.
D) Transportation problems.
E) Assignment problems.
Newspaper stories take 3 hours to write and pay a flat rate of $45 per story. Magazine articles take much longer to write (25 hours) but pay significantly better ($400 per article). Proofreading is often tedious, but the writer can always find proofreading jobs that pay $20 per hour. The writer wants to maximize her income, but doesn't want to work more than 45 hours per week. Additionally, she dislikes proofreading so she would like to spend no more than 7 hours per week on that task. Both newspaper stories and magazine articles must be completed in the week they are started (HINT: use an integer constraint to be sure that all newspaper and magazine jobs are finished within a week).
The writer's problem falls within which classification?
A) Resource-allocation.
B) Cost-benefit-trade-off.
C) Mixed problems.
D) Transportation problems.
E) Assignment problems.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
73
A freelance writer must choose how to spend her time working on several different types of projects.
Newspaper stories take 3 hours to write and pay a flat rate of $45 per story. Magazine articles take much longer to write (25 hours) but pay significantly better ($400 per article). Proofreading is often tedious, but the writer can always find proofreading jobs that pay $20 per hour. The writer wants to maximize her income, but doesn't want to work more than 45 hours per week. Additionally, she dislikes proofreading so she would like to spend no more than 7 hours per week on that task. Both newspaper stories and magazine articles must be completed in the week they are started (HINT: use an integer constraint to be sure that all newspaper and magazine jobs are finished within a week).
Which of the following is the objective function for the writer's problem?
A) Max R = 45N + 400M − 20P
B) Min R = 3N + 25M + P
C) Max R = 45N + 400M + 20P
D) Min R = 3N + 25M + 20P
E) Max R = 3N + 400M + 20P
Newspaper stories take 3 hours to write and pay a flat rate of $45 per story. Magazine articles take much longer to write (25 hours) but pay significantly better ($400 per article). Proofreading is often tedious, but the writer can always find proofreading jobs that pay $20 per hour. The writer wants to maximize her income, but doesn't want to work more than 45 hours per week. Additionally, she dislikes proofreading so she would like to spend no more than 7 hours per week on that task. Both newspaper stories and magazine articles must be completed in the week they are started (HINT: use an integer constraint to be sure that all newspaper and magazine jobs are finished within a week).
Which of the following is the objective function for the writer's problem?
A) Max R = 45N + 400M − 20P
B) Min R = 3N + 25M + P
C) Max R = 45N + 400M + 20P
D) Min R = 3N + 25M + 20P
E) Max R = 3N + 400M + 20P

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
74
A firm has 4 plants that produce widgets. Plants A, B, and C can each produce 100 widgets per day. Plant D can produce 50 widgets per day. Each day, the widgets produced in the plants must be shipped to satisfy the demand of 3 customers. Customer 1 requires 75 units per day, customer 2 requires 100 units per day, and customer 3 requires 175 units per day. The shipping costs for each possible route are shown in the table below:
The firm needs to satisfy all demand each day, but would like to minimize the total costs.
What is the minimum daily shipping cost that the firm can achieve?
A) $6,725
B) $7,125
C) $7,525
D) $7,925
E) $8,325
The firm needs to satisfy all demand each day, but would like to minimize the total costs.
What is the minimum daily shipping cost that the firm can achieve?
A) $6,725
B) $7,125
C) $7,525
D) $7,925
E) $8,325

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
75
A freelance writer must choose how to spend her time working on several different types of projects.
Newspaper stories take 3 hours to write and pay a flat rate of $45 per story. Magazine articles take much longer to write (25 hours) but pay significantly better ($400 per article). Proofreading is often tedious, but the writer can always find proofreading jobs that pay $20 per hour. The writer wants to maximize her income, but doesn't want to work more than 45 hours per week. Additionally, she dislikes proofreading so she would like to spend no more than 7 hours per week on that task. Both newspaper stories and magazine articles must be completed in the week they are started (HINT: use an integer constraint to be sure that all newspaper and magazine jobs are finished within a week).
What is the optimal mix of jobs for the writer to accept each week?
A) N = 13, M = 0, P = 6
B) N = 12, M = 0, P = 7
C) N = 6, M = 1, P = 2
D) N = 5, M = 1, P = 5
E) N = 6, M = 1, P = 0
Newspaper stories take 3 hours to write and pay a flat rate of $45 per story. Magazine articles take much longer to write (25 hours) but pay significantly better ($400 per article). Proofreading is often tedious, but the writer can always find proofreading jobs that pay $20 per hour. The writer wants to maximize her income, but doesn't want to work more than 45 hours per week. Additionally, she dislikes proofreading so she would like to spend no more than 7 hours per week on that task. Both newspaper stories and magazine articles must be completed in the week they are started (HINT: use an integer constraint to be sure that all newspaper and magazine jobs are finished within a week).
What is the optimal mix of jobs for the writer to accept each week?
A) N = 13, M = 0, P = 6
B) N = 12, M = 0, P = 7
C) N = 6, M = 1, P = 2
D) N = 5, M = 1, P = 5
E) N = 6, M = 1, P = 0

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
76
A firm has 4 plants that produce widgets. Plants A, B, and C can each produce 100 widgets per day. Plant D can produce 50 widgets per day. Each day, the widgets produced in the plants must be shipped to satisfy the demand of 3 customers. Customer 1 requires 75 units per day, customer 2 requires 100 units per day, and customer 3 requires 175 units per day. The shipping costs for each possible route are shown in the table below:
The firm needs to satisfy all demand each day, but would like to minimize the total costs.
The firm's problem falls within which classification?
A) Resource-allocation
B) Cost-benefit-trade-off
C) Transshipment problems
D) Transportation problems
E) Assignment problems
The firm needs to satisfy all demand each day, but would like to minimize the total costs.
The firm's problem falls within which classification?
A) Resource-allocation
B) Cost-benefit-trade-off
C) Transshipment problems
D) Transportation problems
E) Assignment problems

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck


