
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 6
Find the amount of the payment needed to accumulate the indicated amount in a sinking fund. Round to the nearest cent. (See Examples.)
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
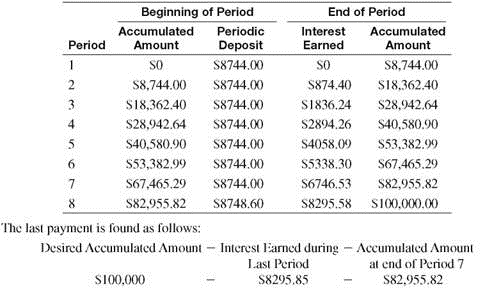
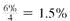 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)

Finding the Periodic Payments
First Christian Church sold $100,000 worth of bonds that must be paid off in 8 years. It now must set up a sinking fund to accumulate the necessary $100,000 to pay off the debt. Find the amount of each payment into a sinking fund if the payments are made at the end of each year and the fund earns 10% compounded annually. Find the amount of interest earned.
SOLUTION
Look along the top of the sinking fund table for 10% and down the side for 8 periods to find.08744.
Payment = $100,000 ×.08744 = $ 8744
The church must deposit $8744 at the end of each year for 8 years into an account paying 10% compounded annually to accumulate $100,000. The interest earned is the future value less all payments.
Interest = $100,000 ? (8 × $8744) = $ 30,048

Setting up a Sinking Fund Table
First Christian Church in Example deposited $8744 at the end of each year for 8 years into a sinking fund that earned 10% compounded annually. Set up a sinking fund table for these deposits. After each calculation, round each answer to the nearest cent before proceeding.
SOLUTION
The sinking fund account contains no money until the end of the first year, when a single deposit of $8744 is made. Since the deposit is made at the end of the year, no interest is earned.
At the end of the second year, the account contains the original $8744 plus the interest earned by this money. This interest is found by the formula for simple interest.
I = $8744 ×.10 × 1 = $874.40
An additional deposit is also made at the end of the second year, so that the sinking fund then contains the following total.
$8744 + $874.40 + $8744 = $18,362.40
Continue this work to get the following sinking fund table.
Quick TIP
Normally the last payment is adjusted as needed so that the future value exactly equals the desired amount. We assume this is true from this point forward.
$32,000, money earns 6% compounded quarterly, 3 years____________
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
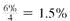 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)

Finding the Periodic Payments
First Christian Church sold $100,000 worth of bonds that must be paid off in 8 years. It now must set up a sinking fund to accumulate the necessary $100,000 to pay off the debt. Find the amount of each payment into a sinking fund if the payments are made at the end of each year and the fund earns 10% compounded annually. Find the amount of interest earned.
SOLUTION
Look along the top of the sinking fund table for 10% and down the side for 8 periods to find.08744.
Payment = $100,000 ×.08744 = $ 8744
The church must deposit $8744 at the end of each year for 8 years into an account paying 10% compounded annually to accumulate $100,000. The interest earned is the future value less all payments.
Interest = $100,000 ? (8 × $8744) = $ 30,048

Setting up a Sinking Fund Table
First Christian Church in Example deposited $8744 at the end of each year for 8 years into a sinking fund that earned 10% compounded annually. Set up a sinking fund table for these deposits. After each calculation, round each answer to the nearest cent before proceeding.
SOLUTION
The sinking fund account contains no money until the end of the first year, when a single deposit of $8744 is made. Since the deposit is made at the end of the year, no interest is earned.
At the end of the second year, the account contains the original $8744 plus the interest earned by this money. This interest is found by the formula for simple interest.
I = $8744 ×.10 × 1 = $874.40
An additional deposit is also made at the end of the second year, so that the sinking fund then contains the following total.
$8744 + $874.40 + $8744 = $18,362.40
Continue this work to get the following sinking fund table.
Quick TIP
Normally the last payment is adjusted as needed so that the future value exactly equals the desired amount. We assume this is true from this point forward.

$32,000, money earns 6% compounded quarterly, 3 years____________
Explanation
The following table is given, There are...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


