An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin

Exercise 26

A mathematical programming system named Silver Screener uses a 0-1 integer programming model to help theater managers decide which movies to show on a weekly basis in a multiple-screen theater ( Interfaces May/June 2001). Suppose that management of Valley Cinemas would like to investigate the potential of using a similar scheduling system for their chain of multiple-screen theaters. Valley selected a small two-screen movie theatre tor the pilot testing and would like to develop an integer programming model to help schedule movies for the next four weeks. Six movies are available. The first week each movie is available, the last week each movie can be shown, and the maximum number of weeks that each movie can run are shown here: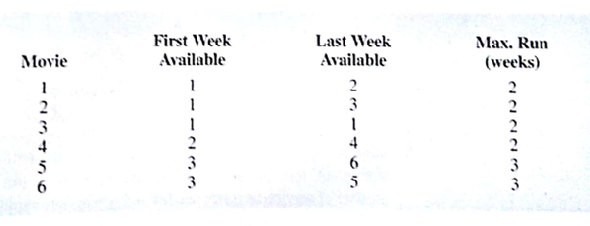
The overall viewing schedule for the theater is composed of the individual schedules for each of the six movies. For each movie, a schedule must be developed that specifies the week the movie starts and the number of consecutive weeks it will run. For instance, one possible schedule for movie 2 is for it to start in week 1 and run for two weeks. Theater policy requires that once a movie is started it must be shown in consecutive weeks. It cannot be stopped and restarted again. To represent the scheduled possibilities for each movie, the following decision variables were developed:
For example x 532 = 1 means that the schedule selected for movie 5 is to begin in week 3 and run for weeks. For each movie. A separate variable is given for each possible schedule.
a. Three schedules are associated with movie 1 List the variables that represent these schedules.
b. Write a constraint requiring that only one schedule be selected for movie 1.
c. Write a constraint requiring that only one schedule be selected for movie 5.
d. What restricts the number of movies that can be selected in week 1? Write a constraint that restricts the number of movies sc selected for viewing in week 1.
e. Write a constraint that restricts the number of movies selected for viewing in week 3.