
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Edition 13ISBN: 978-1439043271
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Edition 13ISBN: 978-1439043271 Exercise 6
This problem requires a basic understanding of the normal probability distribution. Investors are often interested in knowing the probabilities of poor returns. For example, for what cutoff return will the probability of the actual return falling below this cutoff value be at most 1%?
Consider the solution to the Markowitz portfolio problem given in Figure 8.9. The mean return of the portfolio is 10% and the standard deviation (calculated by taking the square root of the variance, which is the objective function value) is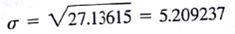
Assume that the portfolio scenario returns are normally distributed about the mean return. From the normal probability table, we see that less than 1% of the returns fall more than 2.33 standard deviations below the mean. This result implies a probability of 1% or less that a portfolio return will fall below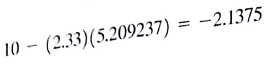
Stated another way, if the initial value of the portfolio is $1, then the investor faces a probability of 1% of incurring a loss of 2.1375 cents or more. The value at risk is 2.1375 cents at 1%. This measure of risk is called the value at risk , or VaR. It was popularized by JPMorgan Chase Co. in the early 1990s (then, just JP Morgan).
A table of normal probabilities appears in Appendix B, but they are also easily calculated in LINGO and Excel. In LINGO the function @PSN(Z) and the equivalent function NORMDIST in Excel provide the probability that a standard normal random variables is less than Z.
a. Consider the Markowitz portfolio problem given in equations (8.10) through (81.9). Delete the required return constraint (8.18), and reformulate this problem to minimize the VaR at 1%.
b. Is minimizing the VaR the same as minimizing the variances of the portfolio? Answer Yes or No, and justify.
c. For a fixed return, is minimizing the VaR the same as minimizing the variances of the portfolio? Answer Yes or No, and justify.
Consider the solution to the Markowitz portfolio problem given in Figure 8.9. The mean return of the portfolio is 10% and the standard deviation (calculated by taking the square root of the variance, which is the objective function value) is
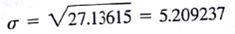
Assume that the portfolio scenario returns are normally distributed about the mean return. From the normal probability table, we see that less than 1% of the returns fall more than 2.33 standard deviations below the mean. This result implies a probability of 1% or less that a portfolio return will fall below
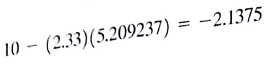
Stated another way, if the initial value of the portfolio is $1, then the investor faces a probability of 1% of incurring a loss of 2.1375 cents or more. The value at risk is 2.1375 cents at 1%. This measure of risk is called the value at risk , or VaR. It was popularized by JPMorgan Chase Co. in the early 1990s (then, just JP Morgan).
A table of normal probabilities appears in Appendix B, but they are also easily calculated in LINGO and Excel. In LINGO the function @PSN(Z) and the equivalent function NORMDIST in Excel provide the probability that a standard normal random variables is less than Z.
a. Consider the Markowitz portfolio problem given in equations (8.10) through (81.9). Delete the required return constraint (8.18), and reformulate this problem to minimize the VaR at 1%.
b. Is minimizing the VaR the same as minimizing the variances of the portfolio? Answer Yes or No, and justify.
c. For a fixed return, is minimizing the VaR the same as minimizing the variances of the portfolio? Answer Yes or No, and justify.
Explanation

This question doesn’t have an expert verified answer yet, let Examlex AI Copilot help.
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


