
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Edition 4ISBN: 978-0324660609
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Edition 4ISBN: 978-0324660609 Exercise 20
Let hy6t denote the three-month holding yield (in percent) from buying a six-month T-bill at time (t - 1) and selling it at time t (three months hence) as a three-month
T-bill. Let hy3t-1 be the three-month holding yield from buying a three-month T-bill at time (t - 1). At time (t - 1), hy3t-1 is known, whereas hy6t is unknown because p3t (the price of three-month T-bills) is unknown at time (t - 1). The expectations hypothesis (EH) says that these two different three-month investments should be the
same, on average. Mathematically, we can write this as a conditional expectation: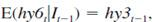
where It-1 denotes all observable information up through time t - 1. This suggests estimating the model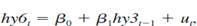 and testing H0: = 1. (We can also test H0: 0 = 0, but we often allow for a term premium for buying assets with different maturities, so that 0 0.)
and testing H0: = 1. (We can also test H0: 0 = 0, but we often allow for a term premium for buying assets with different maturities, so that 0 0.)
(i) Estimating the previous equation by OLS using the data in INTQRT.RAW (spaced every three months) gives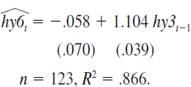
Do you reject H0: 1=1 against H0: 1 1 at the 1% significance level Does the estimate seem practically different from one
(ii) Another implication of the EH is that no other variables dated as t - 1 or earlier should help explain hy6t, once hy3t-1 has been controlled for. Including one lag of the spread between six-month and three-month T-bill rates gives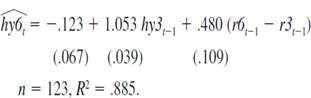
Now, is the coefficient on hy3t - 1 statistically different from one Is the lagged spread term significant According to this equation, if, at time t - 1, r6 is above r3, should you invest in six-month or three-month T-bills
(iii) The sample correlation between hy3t and hy3t - 1 is.914. Why might this raise some concerns with the previous analysis
(iv) How would you test for seasonality in the equation estimated in part (ii)
T-bill. Let hy3t-1 be the three-month holding yield from buying a three-month T-bill at time (t - 1). At time (t - 1), hy3t-1 is known, whereas hy6t is unknown because p3t (the price of three-month T-bills) is unknown at time (t - 1). The expectations hypothesis (EH) says that these two different three-month investments should be the
same, on average. Mathematically, we can write this as a conditional expectation:
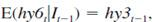
where It-1 denotes all observable information up through time t - 1. This suggests estimating the model
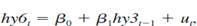 and testing H0: = 1. (We can also test H0: 0 = 0, but we often allow for a term premium for buying assets with different maturities, so that 0 0.)
and testing H0: = 1. (We can also test H0: 0 = 0, but we often allow for a term premium for buying assets with different maturities, so that 0 0.)(i) Estimating the previous equation by OLS using the data in INTQRT.RAW (spaced every three months) gives
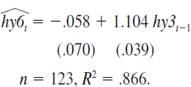
Do you reject H0: 1=1 against H0: 1 1 at the 1% significance level Does the estimate seem practically different from one
(ii) Another implication of the EH is that no other variables dated as t - 1 or earlier should help explain hy6t, once hy3t-1 has been controlled for. Including one lag of the spread between six-month and three-month T-bill rates gives
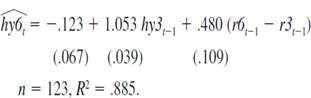
Now, is the coefficient on hy3t - 1 statistically different from one Is the lagged spread term significant According to this equation, if, at time t - 1, r6 is above r3, should you invest in six-month or three-month T-bills
(iii) The sample correlation between hy3t and hy3t - 1 is.914. Why might this raise some concerns with the previous analysis
(iv) How would you test for seasonality in the equation estimated in part (ii)
Explanation
Consider to be three month holding yiel...
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


