Exam 7: Random Variables and Discrete Probability Distributions

A statistical measure of the strength of the relationship between two random variables X and Y is referred to as the:

Number of Motorcycles The probability distribution of a discrete random variable X is shown below, where X represents the number of motorcycles owned by a family. -{Number of Motorcycles Narrative} Find the standard deviation of X.

A function or rule that assigns a numerical value to each outcome of an experiment is called:

A portfolio expected return E(R_p) of 3 stocks with the quantities w₁ = .40, w₂ = .50, w₃ = .10, E(R₁) = .10, E(R₂) = .15, and E(R₃) = .02 is equal to 0.117.

If X and Y are two variables with E(XY) = 10.56, E(X) = 4.22, and E(Y) = 5.34, then COV(X, Y) = 1.0.

Blackjack The probability distribution of a random variable X is shown below, where X represents the amount of money (in $1,000s) gained or lost in a particular game of Blackjack. -{Blackjack Narrative} Find the following values and indicate their units. a. E(X) b. V(X) c. Standard deviation of X

If X and Y are two variables with $\sigma$ _x = 3.8, $\sigma$ _y = 4.2, and COV(X, Y) = -0.25, then V(X + Y) = 31.58.

A binomial experiment consists of a(n) ____________________ number of trials, n.

Retries The following table contains the probability distribution for X = the number of retries necessary to successfully transmit a 1024K data package through a double satellite media. -{Retries Narrative} What is the probability of a least one retry?

If the covariance between two investments of a portfolio is zero, the variance of the portfolio will be equal to the sum of the variances of the investments.

The number of customers arriving at a department store in a 5-minute period has a binomial distribution.

Sports Fans Suppose that past history shows that 5% of college students are sports fans.A sample of 10 students is to be selected. -{Sports Fans Narrative} Find the probability that at least 1 student is a sports fan.

Car Sales The joint probability distribution of variables X and Y is shown in the table below.Rebecca and Rachel are car salespeople.Let X denote the number of cars that Rebecca will sell in a month, and let Y denote the number of cars Rachel will sell in a month. 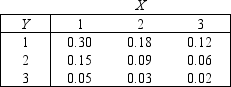-{Car Sales Narrative} Determine the marginal probability distribution of Y.

A random variable is a function or rule that assigns a number to each outcome of an experiment.

Golfing Store The joint probability distribution of variables X and Y is shown in the table below, where X is the number of drivers and Y is the number of putters sold daily in a small golfing store. 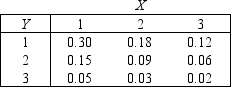-{Golfing Store Narrative} Determine the marginal probability distributions of X and Y.

Katie's Portfolio Katie is given the following information about the returns on two stocks: E(R₁) = 0.10, E(R₂) = 0.15, V(R₁) = 0.0225, and V(R₂) = 0.0441. -{Katie's Portfolio Narrative} If Katie is most interested in minimizing her risk, which stock should she choose?

The binomial distribution deals with consecutive trials, each of which has two possible outcomes.

The number of home insurance policy holders is an example of a discrete random variable

Unsafe Levels of Radioactivity The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year. -{Unsafe Levels of Radioactiviy Narrative} Find the probability that there will be at least 1 incident in a year.

In the Poisson distribution, the mean is equal to the ____________________.