Deck 7: Random Variables and Discrete Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/274
Play
Full screen (f)
Deck 7: Random Variables and Discrete Probability Distributions
1
In a Poisson distribution, the mean and standard deviation are equal.
False
2
The largest value that a Poisson random variable X can have is n.
False
3
The Poisson random variable is a discrete random variable with infinitely many possible values.
True
4
The mean of a Poisson distribution, where is the average number of successes occurring in a specified interval, is .

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
5
On the average, 1.6 customers per minute arrive at any one of the checkout counters of Sunshine food market.What type of probability distribution can be used to find out the probability that there will be no customers arriving at a checkout counter in 10 minutes?
A) Poisson distribution
B) Normal distribution
C) Binomial distribution
D) None of these choices.
A) Poisson distribution
B) Normal distribution
C) Binomial distribution
D) None of these choices.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
6
The Sutton police department must write, on average, 6 tickets a day to keep department revenues at budgeted levels.Suppose the number of tickets written per day follows a Poisson distribution with a mean of 6.5 tickets per day.Interpret the value of the mean.
A) The mean has no interpretation.
B) The expected number of tickets written would be 6.5 per day.
C) Half of the days have less than 6.5 tickets written and half of the days have more than 6.5 tickets written.
D) The number of tickets that is written most often is 6.5 tickets per day.
A) The mean has no interpretation.
B) The expected number of tickets written would be 6.5 per day.
C) Half of the days have less than 6.5 tickets written and half of the days have more than 6.5 tickets written.
D) The number of tickets that is written most often is 6.5 tickets per day.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
7
A community college has 150 word processors.The probability that any one of them will require repair on a given day is 0.025.To find the probability that exactly 25 of the word processors will require repair, one will use what type of probability distribution?
A) Normal distribution
B) Poisson distribution
C) Binomial distribution
D) None of these choices.
A) Normal distribution
B) Poisson distribution
C) Binomial distribution
D) None of these choices.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
8
In a Poisson distribution, the:
A) mean equals the standard deviation.
B) median equals the standard deviation.
C) mean equals the variance.
D) None of these choices.
A) mean equals the standard deviation.
B) median equals the standard deviation.
C) mean equals the variance.
D) None of these choices.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
9
The Poisson distribution is applied to events for which the probability of occurrence over a given span of time, space, or distance is very small.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
10
The number of customers arriving at a department store in a 5-minute period has a Poisson distribution.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
11
Given a Poisson random variable X, where the average number of successes occurring in a specified interval is 1.8, then P(X = 0) is:
A) 1.8
B) 1.3416
C) 0.1653
D) 6.05
A) 1.8
B) 1.3416
C) 0.1653
D) 6.05

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
12
The Poisson probability distribution is a continuous probability distribution.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
13
In a Poisson experiment, the number of successes that occur in any interval of time is ____________________ of the number of success that occur in any other interval.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following cannot have a Poisson distribution?
A) The length of a movie.
B) The number of telephone calls received by a switchboard in a specified time period.
C) The number of customers arriving at a gas station in Christmas day.
D) The number of bacteria found in a cubic yard of soil.
A) The length of a movie.
B) The number of telephone calls received by a switchboard in a specified time period.
C) The number of customers arriving at a gas station in Christmas day.
D) The number of bacteria found in a cubic yard of soil.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
15
The Poisson random variable is a:
A) discrete random variable with infinitely many possible values.
B) discrete random variable with finite number of possible values.
C) continuous random variable with infinitely many possible values.
D) continuous random variable with finite number of possible values.
A) discrete random variable with infinitely many possible values.
B) discrete random variable with finite number of possible values.
C) continuous random variable with infinitely many possible values.
D) continuous random variable with finite number of possible values.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
16
In a(n) ____________________ experiment, the probability of a success in an interval is the same for all equal-sized intervals.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
17
In a Poisson distribution, the mean and variance are equal.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
18
The number of accidents that occur at a busy intersection in one month is an example of a Poisson random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
19
The number of customers making a purchase out of 30 randomly selected customers has a Poisson distribution.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
20
In a Poisson distribution, the variance and standard deviation are equal.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
21
A Poisson random variable is the number of successes that occur in a period of ____________________ or an interval of ____________________ in a Poisson experiment.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
22
Let X be a Poisson random variable with = 6.Use the table of Poisson probabilities to calculate:
a.
P(X 8)
b.
P(X = 8)
c.
P(X 5)
d.
P(6 X 10)
a.
P(X 8)
b.
P(X = 8)
c.
P(X 5)
d.
P(6 X 10)

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
23
Classified Department Phone Calls
A classified department receives an average of 10 telephone calls each afternoon between 2 and 4 P.M.The calls occur randomly and independently of one another.
-{Classified Department Phone Calls Narrative} Find the probability that the department will receive 13 calls between 2 and 4 P.M.on a particular afternoon.
A classified department receives an average of 10 telephone calls each afternoon between 2 and 4 P.M.The calls occur randomly and independently of one another.
-{Classified Department Phone Calls Narrative} Find the probability that the department will receive 13 calls between 2 and 4 P.M.on a particular afternoon.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
24
In the Poisson distribution, the mean is equal to the ____________________.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
25
911 Phone Calls
911 phone calls arrive at the rate of 30 per hour at the local call center.
-{911 Phone Calls Narrative} Find the probability of receiving two calls in a five-minute interval of time.
911 phone calls arrive at the rate of 30 per hour at the local call center.
-{911 Phone Calls Narrative} Find the probability of receiving two calls in a five-minute interval of time.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
26
In the Poisson distribution, the ____________________ is equal to the variance.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
27
Compute the following Poisson probabilities (to 4 decimal places) using the Poisson formula:
a.
P(X = 3), if = 2.5
b.
P(X 1), if = 2.0
c.
P(X 2), if = 3.0
a.
P(X = 3), if = 2.5
b.
P(X 1), if = 2.0
c.
P(X 2), if = 3.0

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
28
911 Phone Calls
911 phone calls arrive at the rate of 30 per hour at the local call center.
-{911 Phone Calls Narrative} Find the probability of receiving exactly eight calls in 15 minutes.
911 phone calls arrive at the rate of 30 per hour at the local call center.
-{911 Phone Calls Narrative} Find the probability of receiving exactly eight calls in 15 minutes.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
29
In Poisson experiment, the probability of more than one success in an interval approaches ____________________ as the interval becomes smaller.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
30
Let X be a Poisson random variable with = 8.Use the table of Poisson probabilities to calculate:
a.
P(X 6)
b.
P(X = 4)
c.
P(X 3)
d.
P(9 X 14)
a.
P(X 6)
b.
P(X = 4)
c.
P(X 3)
d.
P(9 X 14)

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
31
A Poisson random variable is a(n) ____________________ random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
32
Classified Department Phone Calls
A classified department receives an average of 10 telephone calls each afternoon between 2 and 4 P.M.The calls occur randomly and independently of one another.
-{Classified Department Phone Calls Narrative} Find the probability that the department will receive at least five calls between 2 and 4 P.M.on a particular afternoon.
A classified department receives an average of 10 telephone calls each afternoon between 2 and 4 P.M.The calls occur randomly and independently of one another.
-{Classified Department Phone Calls Narrative} Find the probability that the department will receive at least five calls between 2 and 4 P.M.on a particular afternoon.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
33
The possible values of a Poisson random variable start at ____________________.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
34
In a Poisson experiment, the probability of a success in an interval is ____________________ to the size of the interval.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
35
911 Phone Calls
911 phone calls arrive at the rate of 30 per hour at the local call center.
-{911 Phone Calls Narrative} If no calls are currently being processed, what is the probability that the desk employee can take four minutes break without being interrupted?
911 phone calls arrive at the rate of 30 per hour at the local call center.
-{911 Phone Calls Narrative} If no calls are currently being processed, what is the probability that the desk employee can take four minutes break without being interrupted?

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
36
Post office
The number of arrivals at a local post office between 3:00 and 5:00 P.M.has a Poisson distribution with a mean of 12.
-{Post Office Narrative} Find the probability that the number of arrivals between 3:00 and 5:00 P.M.is at least 10.
The number of arrivals at a local post office between 3:00 and 5:00 P.M.has a Poisson distribution with a mean of 12.
-{Post Office Narrative} Find the probability that the number of arrivals between 3:00 and 5:00 P.M.is at least 10.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
37
Post office
The number of arrivals at a local post office between 3:00 and 5:00 P.M.has a Poisson distribution with a mean of 12.
-{{Post Office Narrative} Find the probability that the number of arrivals between 4:00 and 5:00 P.M.is exactly two.
The number of arrivals at a local post office between 3:00 and 5:00 P.M.has a Poisson distribution with a mean of 12.
-{{Post Office Narrative} Find the probability that the number of arrivals between 4:00 and 5:00 P.M.is exactly two.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
38
Post office
The number of arrivals at a local post office between 3:00 and 5:00 P.M.has a Poisson distribution with a mean of 12.
-{Post Office Narrative} Find the probability that the number of arrivals between 3:30 and 4:00 P.M.is at least 10.
The number of arrivals at a local post office between 3:00 and 5:00 P.M.has a Poisson distribution with a mean of 12.
-{Post Office Narrative} Find the probability that the number of arrivals between 3:30 and 4:00 P.M.is at least 10.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
39
Classified Department Phone Calls
A classified department receives an average of 10 telephone calls each afternoon between 2 and 4 P.M.The calls occur randomly and independently of one another.
-{Classified Department Phone Calls Narrative} Find the probability that the department will receive seven calls between 2 and 3 P.M.on a particular afternoon.
A classified department receives an average of 10 telephone calls each afternoon between 2 and 4 P.M.The calls occur randomly and independently of one another.
-{Classified Department Phone Calls Narrative} Find the probability that the department will receive seven calls between 2 and 3 P.M.on a particular afternoon.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
40
The ____________________ of a Poisson distribution is the rate at which successes occur for a given period of time or interval of space.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
41
Unsafe Levels of Radioactivity
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the probability that there will be at least 3 incidents in a year.
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the probability that there will be at least 3 incidents in a year.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
42
The time required to drive from New York to New Mexico is a discrete random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
43
The number of home insurance policy holders is an example of a discrete random variable

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
44
The amount of milk consumed by a baby in a day is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
45
Given that X is a discrete random variable, then the laws of expected value and variance can be applied to show that E(X + 5) = E(X) + 5, and V(X + 5) = V(X) + 25.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
46
Unsafe Levels of Radioactivity
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the probability that there will be no more than 1 incident in a year.
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the probability that there will be no more than 1 incident in a year.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
47
Faculty rank (professor, associate professor, assistant professor, and lecturer) is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
48
The number of homeless people in Boston is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
49
Another name for the mean of a probability distribution is its expected value.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
50
The length of time for which an apartment in a large complex remains vacant is a discrete random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
51
Unsafe Levels of Radioactivity
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the variance of the number of incidents in one year.
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the variance of the number of incidents in one year.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
52
A table, formula, or graph that shows all possible values a random variable can assume, together with their associated probabilities, is referred to as probability distribution.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
53
Suppose that the number of buses arriving at a Depot per minute is a Poisson process.If the average number of buses arriving per minute is 3, what is the probability that exactly 6 buses arrive in the next minute?

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
54
Unsafe Levels of Radioactivity
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the probability that there will be exactly 3 incidents in a year.
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the probability that there will be exactly 3 incidents in a year.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
55
The mean of a discrete probability distribution for X is the sum of all possible values of X, divided by the number of possible values of X.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
56
A continuous variable may take on any value within its relevant range even though the measurement device may not be precise enough to record it.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
57
A random variable is a function or rule that assigns a number to each outcome of an experiment.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
58
Unsafe Levels of Radioactivity
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the standard deviation of the number of incidents is in one year.
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactivity Narrative} Find the standard deviation of the number of incidents is in one year.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
59
Unsafe Levels of Radioactivity
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactiviy Narrative} Find the probability that there will be at least 1 incident in a year.
The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year.
{Unsafe Levels of Radioactiviy Narrative} Find the probability that there will be at least 1 incident in a year.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
60
For a random variable X, if V(cX) = 4V(X), where V refers to the variance, then c must be 2.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
61
Which of the following are required conditions for the distribution of a discrete random variable X that can assume values xi?
A) 0 p(xi) 1 for all xi
B)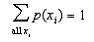
C) Both a and b are required conditions.
D) Neither a nor b are required conditions.
A) 0 p(xi) 1 for all xi
B)
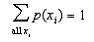
C) Both a and b are required conditions.
D) Neither a nor b are required conditions.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
62
A motorcycle insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for motorcycle insurance.How long a person has been a licensed rider is an example of a(n) ____________________ random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
63
The dean of students conducted a survey on campus.Grade point average (GPA) is an example of a(n) ____________________ random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
64
Which of the following is not a required condition for the distribution of a discrete random variable X that can assume values xi?
A) 0 p(xi) 1 for all xi
B)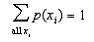
C) p(xi) > 1 for all xi
D) All of these choices are true.
A) 0 p(xi) 1 for all xi
B)
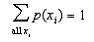
C) p(xi) > 1 for all xi
D) All of these choices are true.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
65
An auto insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for automobile insurance.A person's age is an example of a(n) ____________________ random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
66
For a random variable X, V(X + 3) = V(X + 6), where V refers to the variance.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
67
In the notation below, X is the random variable, c is a constant, and V refers to the variance.Which of the following laws of variance is not true?
A) V(c) = 0
B) V(X + c) = V(X) + c
C) V(cX) = c2 V(X)
D) None of these choices.
A) V(c) = 0
B) V(X + c) = V(X) + c
C) V(cX) = c2 V(X)
D) None of these choices.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
68
For a random variable X, E(X + 2) - 5 = E(X) - 3, where E refers to the expected value.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
69
A motorcycle insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for motorcycle insurance.The distance a person rides in a year is an example of a(n) ____________________ random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
70
A motorcycle insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for motorcycle insurance.The number of tickets a person has received in the last 3 years is an example of a(n) ____________________ random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
71
Which of the following is a continuous random variable?
A) The number of employees of an automobile company.
B) The amount of milk produced by a cow in one 24-hour period.
C) The number of gallons of milk sold at Albertson's grocery store last week.
D) None of these choices.
A) The number of employees of an automobile company.
B) The amount of milk produced by a cow in one 24-hour period.
C) The number of gallons of milk sold at Albertson's grocery store last week.
D) None of these choices.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
72
The number of accidents that occur annually on a busy stretch of highway is an example of:
A) a discrete random variable.
B) a continuous random variable.
C) expected value of a discrete random variable.
D) expected value of a continuous random variable.
A) a discrete random variable.
B) a continuous random variable.
C) expected value of a discrete random variable.
D) expected value of a continuous random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
73
The amount of time that a microcomputer is used per week is an example of a(n) ____________________ random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
74
A table, formula, or graph that shows all possible values a random variable can assume, together with their associated probabilities, is called a(n):
A) probability distribution.
B) discrete random variable.
C) expected value of a discrete random variable.
D) None of these choices.
A) probability distribution.
B) discrete random variable.
C) expected value of a discrete random variable.
D) None of these choices.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
75
A function or rule that assigns a numerical value to each outcome of an experiment is called:
A) a sample space.
B) a probability distribution.
C) a random variable.
D) None of these choices.
A) a sample space.
B) a probability distribution.
C) a random variable.
D) None of these choices.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
76
The weighted average of the possible values that a random variable X can assume, where the weights are the probabilities of occurrence of those values, is referred to as the:
A) variance.
B) standard deviation.
C) expected value.
D) None of these choices.
A) variance.
B) standard deviation.
C) expected value.
D) None of these choices.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
77
A lab at the DeBakey Institute orders 150 rats a week for each of the 52 weeks in the year for experiments that the lab conducts.Suppose the mean cost of rats used in lab experiments turned out to be $20.00 per week.Interpret this value.
A) Most of the weeks resulted in rat costs of $20.00
B) The median cost for the distribution of rat costs is $20.00
C) The expected or average costs for all weekly rat purchases is $20.00
D) The rat cost that occurs more often than any other is $20.00
A) Most of the weeks resulted in rat costs of $20.00
B) The median cost for the distribution of rat costs is $20.00
C) The expected or average costs for all weekly rat purchases is $20.00
D) The rat cost that occurs more often than any other is $20.00

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
78
An auto insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for automobile insurance.The number of claims a person has made in the last 3 years is an example of a(n) ____________________ random variable.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
79
In the notation below, X is the random variable, E and V refer to the expected value and variance, respectively.Which of the following is false?
A) E(3X) = 3E(X)
B) V(2) = 0
C) E(X + 1) = E(X) + 1
D) All of these choices are true.
A) E(3X) = 3E(X)
B) V(2) = 0
C) E(X + 1) = E(X) + 1
D) All of these choices are true.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck
80
Which of the following is a discrete random variable?
A) The Dow Jones Industrial average.
B) The volume of water in Michigan Lakes.
C) The time it takes you to drive to school.
D) The number of employees of a soft drink company.
A) The Dow Jones Industrial average.
B) The volume of water in Michigan Lakes.
C) The time it takes you to drive to school.
D) The number of employees of a soft drink company.

Unlock Deck
Unlock for access to all 274 flashcards in this deck.
Unlock Deck
k this deck


